Journal of Modern Physics
Vol.06 No.13(2015), Article ID:60426,5 pages
10.4236/jmp.2015.613183
On Unparticle Searches through Photon-Photon Scattering
Trieu Quynh Trang, Ha Huy Bang, Nguyen Thu Huong, Sa Thi Lan Anh
Faculty of Physics, Hanoi University of Sciences, Vietnam National University, Hanoi, Vietnam
Email: c25tuan@gmail.com, hahuybang@hus.edu.vn
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 28 August 2015; accepted 16 October 2015; published 21 October 2015
ABSTRACT
In this work, we study the effects of the spin-0 unparticle on γγ ® γγ process. From the numerical results, we show that the cross section with unparticle effect should be about 1027 - 1030 times larger than the one that is confirmed by QED calculation. This could have important implications for unparticle searches and for the measurement of the photon-photon cross section.
Keywords:
Unparticle Physics, Photon-Photon Scattering

1. Introduction
Photon-photon scattering is among the most important and carefully studied processes in particle physics [1] - [13] . In ref. [12] Liang and Czarnecki have shown a simple way of correctly computing the low-energy γγ scattering. Noterworthy, in ref. [13] , we have pointed out the cross section with radion effect should be about 1020 times larger than the one without radion effects. It is well known that Georgi [14] made an interesting observation that a nontrivial scale invariance sector of scale dimension  might manifest itself at low energy as a nonintegral number
might manifest itself at low energy as a nonintegral number 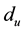 of invisible massless particles, dubbed unparticle u. If unparticles exist, their phenomenological implications should be discussed. In the literature, there have been many discussions which investigate various features of unparticle physics [15] -[24] . In some of these reseaches several unparticle production processes have been studied. Possible evidence for this scale invariant sector might be the signature of a missing energy. It can be tested experimentally by examining missing energy distributions. Other evidence for unparticles can be explored by studying its virtual effects. In this letter, we consider the phenomenology of unparticle signals in γγ scattering. The unparticle analysis of γγ scattering has been done first by Cakir and Ozansoy [25] and later by Chang, Cheung and Yuan [26] . This scattering is described by the Feynman diagrams presented in Figure 1.
of invisible massless particles, dubbed unparticle u. If unparticles exist, their phenomenological implications should be discussed. In the literature, there have been many discussions which investigate various features of unparticle physics [15] -[24] . In some of these reseaches several unparticle production processes have been studied. Possible evidence for this scale invariant sector might be the signature of a missing energy. It can be tested experimentally by examining missing energy distributions. Other evidence for unparticles can be explored by studying its virtual effects. In this letter, we consider the phenomenology of unparticle signals in γγ scattering. The unparticle analysis of γγ scattering has been done first by Cakir and Ozansoy [25] and later by Chang, Cheung and Yuan [26] . This scattering is described by the Feynman diagrams presented in Figure 1.
Figure 1. Feynman diagram for the gamma gamma scattering through a scalar unparticle.
The γγ u vertex is given by
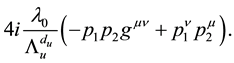 (1)
(1)
The spin-0 unparticle propagator is [27] [28]
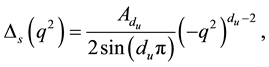 (2)
(2)
where
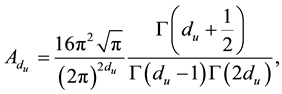 (3)
(3)
and
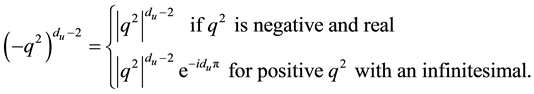
The angular distribution is [26]
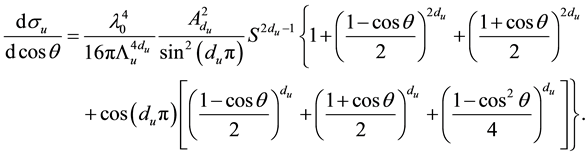 (4)
(4)
From (4), the total cross section is found to be [26]
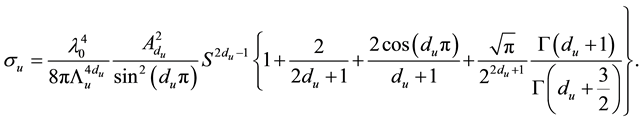 (5)
(5)
We now turn to the numerical analysis of the total cross sections. The input parameters are 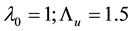 TeV. The total cross section for the unparticle contributions for
TeV. The total cross section for the unparticle contributions for 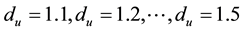 at different ener- gies is given in Table 1.
at different ener- gies is given in Table 1.
It is to be noticed that in refs. [10] [12] the authors have determined the differential and total cross section for the photon-photon scattering without radion and unparticle effects
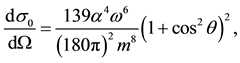 (6)
(6)
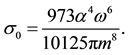 (7)
(7)
Next, in ref. [13] we have investigated the effect of the radion on photon-photon scattering. We obtained the total cross section as follows
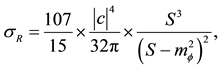 (8)
(8)
with ,
,
where  are the
are the 
The form factors are given by
with
The important property of 





From this, we have found that the effects of the radion can be strong. Interestingly, we have shown that the cross section with radion effect should be about 1020 times larger than the one without radion and unparticle effects. Now, by the results just mentioned we give the numerical values of the ratio of the total cross section with unparticle effects 

So, direct computations have showed that the above cross section of (5) should be about 1027 - 1030 times larger than the one in (7).
Finally, we have obtained the ratio of the cross section with unparticle effects 



Table 1. The total cross section with radion effects of the process 

Table 2. The ratio of the total cross section with unparticle effects to one without radion and unparticle effects at different energies.
Table 3. The ratio of the total cross section with unparticle effects to one with radion effects at different energies.
It has already been shown that the total cross section 

To conclude, in this letter we have studied the unparticle effects on gamma gamma scattering. From numerical results, we have found that the effects of the unparticle on the cross sections can be very strong. If the measure- ment is carried out at

Cite this paper
Trieu QuynhTrang,Ha HuyBang,Nguyen ThuHuong,Sa Thi LanAnh, (2015) On Unparticle Searches through Photon-Photon Scattering. Journal of Modern Physics,06,1798-1802. doi: 10.4236/jmp.2015.613183
References
- 1. Halpern, O. (1993) Scattering Processes Produced by Electrons in Negative Energy States. Physics Review, 44, 855.
http://dx.doi.org/10.1103/PhysRev.44.855.2 - 2. Euler, H. and Kockel, B. (1935) The Scattering of Light by Light in the Dirac Theory. Naturwissenschaften, 23, 246-247.
http://dx.doi.org/10.1007/BF01493898 - 3. Euler, H. (1936) On the Scattering of Light by Light in Dirac’s Theory. Annalen der Physik, 26, 398-448.
http://dx.doi.org/10.1002/andp.19364180503 - 4. Akhieser, A., Landau, L. and Pomeranchook, I. (1937) Scattering of Light by Light. Nature, 138, 206.
http://dx.doi.org/10.1038/138206a0 - 5. Akhieser, A. (1937) Phys. Zeit. Sowjetuion, 11, 263.
- 6. Karplus, R. and Neuman, M. (1950) Non-Linear Interactions between Electromagnetic Fields. Physics Review, 80, 380.
http://dx.doi.org/10.1103/PhysRev.80.380 - 7. Karplus, R. and Neuman, M. (1951) The Scattering of Light by Light. Physics Review, 83, 776.
http://dx.doi.org/10.1103/PhysRev.83.776 - 8. Dittrich, W. and Gies, H. (2000) Effective Lagrangians in Quantum Electrodynamics. Springer Tracts Mod. Phys, 166, 1.
- 9. Kanda, N. (2011) Light-Light Scattering.
http://arxiv.org/abs/1106.0592 - 10. Fujita, T. and Kanda, N. (2011) A Proposal to Measure Photon-Photon Scattering.
http://arxiv.org/abs/1106.0465 - 11. Bernard, D. (2011) Comment on: A Proposal to Measure Photon-Photon Scattering.
http://arxiv.org/pdf/1106.0610.pdf - 12. Liang, Y. and Czarnecki, A. (2011) Photon-Photon Scattering: A Tutorial.
http://arxiv.org/pdf/1111.6126.pdf - 13. Trang, T.Q. and Bang, H.H. (2015) Radion Effects on Gamma Gamma Scattering. Modern Physics Letters A, 30, Article ID: 1550095.
- 14. Georgi, H. (2007) Unparticle Physics. Physical Review Letters, 98, Article ID: 221601.
http://arxiv.org/abs/hep-ph/0703260 http://dx.doi.org/10.1103/physrevlett.98.221601 - 15. Cheung, K., Keung, W.-Y. and Yuan, T.-C. (2007) Collider Phenomenology of Unparticle Physics. Physical Review D, 76, Article ID: 055003.
http://dx.doi.org/10.1103/physrevd.76.055003 - 16. Luo, M.X. and Zhu, G.H. (2008) Some Phenomenologies of Unparticle Physics. Physics Letters B, 659, 341-344. http://dx.doi.org/10.1016/j.physletb.2007.10.058
- 17. He, X.G. (2009) Darkon Dark Matter, Unparticle Effects and Collider Physics. Chinese Physics C, 33, 451-455.
- 18. Georgi, H. (2010) Unparticle Self-Interactions. International Journal of Modern Physics A, 25, 573.
http://dx.doi.org/10.1007/jhep02(2010)065 - 19. Bian, L.G. and Wei, Z.T. (2011) Constraints of Unparticle Physics Parameters from mixing.
http://arxiv.org/abs/1108.1538 - 20. Fortin, J.F., Grinstein, B. and Stergiou, A. (2011) Cyclic Unparticle Physics. Physics Letters B, 709, 408-412.
http://dx.doi.org/10.1016/j.physletb.2012.02.046 - 21. Dahiya, M.D., Dutta, S. and Islam, R. (2012) Constraining Unparticle from Top Physics at Tevatron. Physical Review D, 86, Article ID: 115022.
http://dx.doi.org/10.1103/physrevd.86.115022 - 22. Sun, K.S., Feng, T.-F., Gao, T.-J. and Zhao, S.-M. (2012) Search for Lepton Flavor Violation in Supersymmetric Model via Meson Decays. Nuclear Physics B, 865, 486-508.
http://dx.doi.org/10.1016/j.nuclphysb.2012.08.005 - 23. Khatibi, S. and Najafabadi, M.M. (2013) Top Quark Asymmetries and Unparticle Physics at the Tevatron and LHC. Physical Review D, 87, Article ID: 037701.
http://dx.doi.org/10.1103/physrevd.87.037701 - 24. Aliane, I., Mebarki, N. and Delenda, Y. (2014) Gauged Unparticle Contribution to the Neutrino Anomalous Dipole Moment. Physics Letters B, 728, 549-553.
http://dx.doi.org/10.1016/j.physletb.2013.12.032 - 25. Cakir, O. and Ozansoy, K.O. (2007) Unparticle Searches through Gamma Gamma Scattering.
http://arxiv.org/abs/0712.3814 - 26. Chang, C.F. Cheung, K. and Yuan, T.C. (2008) Unparticle Effects in Photon-Photon Scattering. Physics Letters B, 664, 291-294.
http://arxiv.org/abs/0801.2843
http://dx.doi.org/10.1016/j.physletb.2008.05.039 - 27. Georgi, H. (2007) Another Odd Thing about Unparticle Physics. Physics Letters B, 650, 275-278.
http://arxiv.org/abs/0704.2457 - 28. Cheung, K., Keung, W.Y. and Yuan, T.C. (2007) Collider Signals of Unparticle Physics. Physical Review Letters, 99, Article ID: 051803.
http://arxiv.org/abs/0704.2588







