Journal of Modern Physics
Vol.06 No.09(2015), Article ID:58622,5 pages
10.4236/jmp.2015.69127
A New Interpretation of the Hubble Law
Pascal Churoux
Montgailhard, France
Email: pascal.churoux@free.fr
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 11 June 2015; accepted 1 August 2015; published 6 August 2015
ABSTRACT
We propose a new interpretation of Hubble law. Waves are observed in the observer space-time. It defines the observer proper time T. Space-time is composed of three spatial dimensions and three temporal parameters: proper-time s of the observed object, proper time T of the observer and integration time t (currently considered as relative time). Time origin is the birth of the universe. So, universe is stable; it can be seen as the comobile space of expansion theory. When changing space-time from the source to the observer, waves are seen cooling; this explains the redshift effect. The distance is defined as the product of the delay time with the local speed of light of the observer. The mistake between t and T can explain why universe is viewed as not only in expansion but also in acceleration whereas we think it is stable.
Keywords:
Hubble Law, Space-Time, Light Speed, Universe Expansion, Redshift

1. Introduction
Up to now, physics laws are based on Einstein relativity, established in 1905. Hubble has discovered the correlation between redshift and distance [1] . Cosmology is based on an interpretation of the redshift as expansion [2] through the ΛCDM model.
This article proposes a new approach to explain Hubble law. Other alternatives to expansion have been proposed such as Zwicky in 1929 [3] . Here, we propose a model without expansion and based on a new space-time notion. It defines the local proper time of the observer. Space-time relationship is changing from the observed source to the observer.
First we present the model and then we discuss the interpretation of redshift applied to black body radiation. We compare the proposed model to measured data in the distance modulus―redshift diagram. At the end we explain why, in present interpretation, universe is viewed expanding and moreover accelerating [4] whereas we think it is stable.
2. Proposition of the New Universe Cooling Theory
2.1. Presentation
Using Euclidean space, the observer position is xo. His proper time is T. Time begins at universe origin. The observer detects light from an object in position xe, with a proper time s. Their separation distance is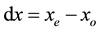 . t is the integration time. We define the time law, derived from the Einstein theory, of the cooling theory presented in one dimension form such as:
. t is the integration time. We define the time law, derived from the Einstein theory, of the cooling theory presented in one dimension form such as:
 (2.1A)
(2.1A)
Let’s consider light propagating from the object to the observer. The boundary conditions are 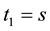 at the beginning and
at the beginning and  at the end. Light follows geodesic lines so that
at the end. Light follows geodesic lines so that . So, from Equation (2.1A) we deduce
. So, from Equation (2.1A) we deduce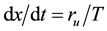 , and then
, and then
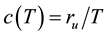 (2.1B)
(2.1B)
On the short term, this result is compatible with relativity (Minkowsky metric) written in times, with
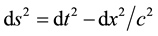 , knowing that
, knowing that 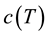 doesn’t vary much with time T (T ~ 13.7 × 109 years from [5] ). This model gives the idea that light speed decreases with time. That is a corpuscular point of view not well suited. It is better to view it as a space-time relation that generates a cooling phenomenon of waves as will be explained later.
doesn’t vary much with time T (T ~ 13.7 × 109 years from [5] ). This model gives the idea that light speed decreases with time. That is a corpuscular point of view not well suited. It is better to view it as a space-time relation that generates a cooling phenomenon of waves as will be explained later.
In this model, product 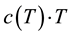 is constant. This suggests that universe radius ru is constant. It defines the Euclidean space. All present physics remains locally valid, only long scales interpretations are modified and explained without matter effects. Physical quantities and laws applied to matter in each space-time are universals. This model is compatible with the restricted theory, using
is constant. This suggests that universe radius ru is constant. It defines the Euclidean space. All present physics remains locally valid, only long scales interpretations are modified and explained without matter effects. Physical quantities and laws applied to matter in each space-time are universals. This model is compatible with the restricted theory, using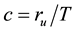 . As we will see in Section 2.2, it is compatible with black body theory because it generates a cooling phenomenon.
. As we will see in Section 2.2, it is compatible with black body theory because it generates a cooling phenomenon.
More than speed light,  represents the relationship between space and time. The proposed model suggests that the space-time is bounded to the observer. He analyzes waves in his own space-time. The delay time between light emission and reception is
represents the relationship between space and time. The proposed model suggests that the space-time is bounded to the observer. He analyzes waves in his own space-time. The delay time between light emission and reception is . So, due to boundary conditions,
. So, due to boundary conditions,
 (2.1C)
(2.1C)
A distance x is defined as the product of delay time τ by the local space-time relation c(T), with
 (2.1D)
(2.1D)
2.2. Application to the Black Body Radiation
The black body theory is local. It can be applied to a volume as little as possible. So it is not affected by the proposed theory. The Planck black body radiation law is:
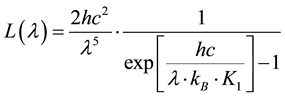 (2.2A)
(2.2A)
where c is the speed of light in vacuum, h is the Planck constant, kB is the Boltzmann constant, K1 is the temperature in Kelvin (˚K), λ is the wavelength in meters (m). 
c = 299792458 m/s; h = 6.62606957 × 10−34 J∙s; kB = 1.3806488 × 10−23 J/˚K. Constants are from [6] .
We write again the Planck law assuming radiation has been emitted at the proper time s. In Equation (2.2A), we replace c by the local space-time relation at the time s of light emission, so 
We make appear the observer proper time T in the above expression.
In the observer space-time 

We deduce:

Equation (2.2C) is the source radiation interpreted as a cooling black body in the observer space-time. The temperature decreases from K1 to K2 with
so

Equation (2.2D) suggests that the product K.T is constant. Today, based on the cosmic background radiation temperature from [7] with K = 2.725 K and T = 13.7 × 109 years from [5] , we get K.T = 1.18 × 1018 K.s.
Now, in Equation (2.2C), the factor z + 1 is gathered with wavelength, so we get

In Equation (2.2E), cooling generates two effects:
The first one is the redshift of the source spectrum, wavelengths are divided by the (z + 1) factor.
The second one is the total reduction of the radiance which is divided by the 
In the expansion theory, the 
2.3. The Hubble Law
In the present expansion theory distance x is related to redshift z using FLWR metric [10] and for z ~ 0,

L. A. Marosi proposes in [11] an empirical law (from 280 measurements) illustrated by Figure 1.
The fitted curve is:

with a = 44.109769 and b = 0.059883 for
Let us now analyze the Hubble law under the proposed cooling theory. We first deal with the distance. We deduce from Equation (2.2B)

The distance x from object to observer is defined by Equation (2.1D) and using Equation (2.1B)
Figure 1. Empirical model of the μ-z diagram, from [11] .

Using Equation (2.1C) and Equation (2.3C)

Using Equation (2.3E) and Equation (2.3F)

For z ~ 0, Equation (2.3G) and Equation (2.1B) gives
Let’s now deal with the radiation. When measuring a radiation, we assume that it follows a law such as

where L is the intrinsic radiation, x is the distance from object to observer. That is due to the assumption of the energy conservation so the product 


where L0 is the apparent intrinsic radiation. We deduce from Equation (2.3G), Equation (2.3H) and Equation (2.3I):
So,
The magnitude is defined by
Then
where
The distance modulus μ is defined by μ = m − m0. So,

Figure 2 presents the empirical model from [3] Equation (2.3B) and the proposed cooling theory Equation (2.3J). Distance unit is in tenth of parsecs with 
We note the very good agreement between the two curves. The remaining deviation is less than 0.2 distance modulus. This can be seen as a validation of the proposed theory which uses only time and space-time relationship.
3. What We Think Is Wrong in Present Expansion Model
The Hubble parameter H and the acceleration parameter 

and

where 



We deduce from Equation (3A) and Equation (3C)
Figure 2. μ-z diagram. Solid line: cooling universe model with ru = 420 × 106 tenth of parsec Equation (2.3J). Dashed line: the empirical model from [11] μ = 44.109769 z0.059883.

so,

But, as we propose in the cooling universe theory, by introducing the observer proper time, at date t = T, Equation (3C) becomes,

We deduce from Equation (3A) and Equation (3F)

Equation (3D) and Equation (3G) are not compatible. Equation (3G) applied into Equation (3B) leads to
T is not the integration time t. No solution can be found when using a metric such as, at first order,

Research is for the moment looking toward expansion and gravitational interpretation of phenomenon. It is using more and more complex gravitation point of view.
We shall not go further on present cosmological metric analysis, because they are only based on gravitational effects. We think that gravitation is a local effect.
4. Conclusions
We propose a new model to explain the µ-z diagram. This diagram represents time between the observed object and the observer. It can be explained without gravitational effects. Space-time is changing between the light source and the observer. 
The proposed model is compatible with the Einstein Universe. When Einstein postulated the constancy of speed of light, the good idea was that the waves are always viewed in the space-time of the observer and so independent with t. Universe is stable, not expanding and not accelerating by the current space-time point of view.
Cite this paper
PascalChuroux, (2015) A New Interpretation of the Hubble Law. Journal of Modern Physics,06,1227-1232. doi: 10.4236/jmp.2015.69127
References
- 1. Hubble, E. and Humason, M.L. (1931) The Astrophysical Journal, 74, 43.
http://dx.doi.org/10.1086/143323 - 2. Suzuki, et al. (2011) The Astrophysical Journal, 746, 85.
- 3. Zwicky, F. (1929) PNAS, 15, 773-779. http://dx.doi.org/10.1073/pnas.15.10.773
- 4. Riess, A.G., et al. (1998) The Astronomical Journal, 116, 1009-1038. http://dx.doi.org/10.1086/300499
- 5. Wang, X.F., et al. (2006) The Astrophysical Journal, 645, 488, 505.
- 6. NIST Standard Reference. http://physics.nist.gov/cuu/Constants/index.html
- 7. Wright, E. (2006) Cosmic Microwave Background. Encyclopedia of Astronomy and Astrophysics. IOP Publishing Ltd., Bristol.
- 8. Lopez-Corredoira, M. (2003) Astronomy & Astrophysics, 1, 561. arXiv:astro-ph/0310214
- 9. Goldhaber, G., Groom, D.E., Kim, A., et al. (2001) The Astrophysical Journal, 558, 359.
http://dx.doi.org/10.1086/322460 - 10. Pettini, M. (2014) The Hubble Diagram of Type 1A Supernovae Evidence for a Cosmological Constant. Physical Cosmology, Lecture 6.
http://www.ast.cam.ac.uk/~pettini/Physical%20Cosmology/lecture06.pdf - 11. Marosi, L.A. (2014) Journal of Modern Physics, 5, 29-33. http://dx.doi.org/10.4236/jmp.2014.51005











