Journal of Modern Physics
Vol.06 No.04(2015), Article ID:54831,6 pages
10.4236/jmp.2015.64043
A Simplified Approach to the Problems of Room-Temperature Superconductivity
Yuri Prazdnikov
Faculty of Physics, Moscow State University, Moscow, Russia
Email: yuriprazdnikov@yandex.ru
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 12 December 2014; accepted 17 March 2015; published 19 March 2015
ABSTRACT
An attempt to simplify the approach to the problems of room-temperature superconductors was done. The key factor has been highlighted―a giant spin-orbit interaction as a result of specific geometry of crystal. Considering oriented carbyne as an example, it was shown that maximal value of SOC was attained in low-dimensional systems. A qualitative model of superconductivity in the localized phase with “pseudo-magnetic field” and “Rashba effective field” as parameters was presented. Their correlation was shown via geometry of electric microfields of crystal. Oriented carbyne was presented as localized phase of room-temperature superconductor and the recipe of its transformation to macroscopic superconductivity was given.
Keywords:
Oriented Carbyne, Topological Insulator, High-Temperature Superconductivity, Pseudo-Magnetic Field

1. Introduction
There is still no simple model of high-temperature superconductivity (HTSC). This model is needed for the development of room-temperature superconductors as well. Currently this area of physics is developed by cut- and-try approach, though it is well-funded. Despite the complexity of the subject and a large number of ideas, there are few attempts to find a unified and simplified approach. This is radically different from the classical theory of low-temperature superconductivity with its clear and simple essence consisting in pairing of electrons. There’s still no result in numerous attempts of usage of this theory for HTSC data. There are disputes if there is a pairing of electrons or not. The force which pairs the electrons should be very powerful to overcome the thermal oscillations. The class of HTSC itself consists of completely different materials compared with LTSC class; they are complex compounds with dopants, which are often not conductors at room temperature at all. The superconductivity is two-dimensional in them. “Pseudogap” state and a diagram showing the dependence of the quantum state of the degree of doping are strange. Pseudogap state is subjected to complex researches, but a simple model still does not exist. A theory in which the superconducting and charge-density wave orders exhibit angular fluctuations in a six-dimensional space is presented in [1] . This theory provides a natural quantitative fit to the experimental data but cannot give us understanding of the pseudogap nature. This example shows the complexity of the features of HTSC, so survey in one article is impossible. Our goal is another to find a simplified micro-approach. From this point of view, it is interesting to note the detection of topological insulator (TI) state in HTSC and term “topological superconductivity” [2] .
There are a lot of results pointing on the existence of room-temperature superconductivity. Mostly it is so called “granular superconductivity” in carbon materials. It is important to say that carbon samples are hydrogenated almost in all cases. In [3] the analysis of “granular superconductivity” is presented. Such physical principles, based on which the superconductivity can exist at temperatures higher than room temperature, are discussed. The “granular superconductivity” is obtained on materials which are disordered hydrogenated mixture of carbon phases. It is extremely difficult to understand which exact atoms’ configuration provides superconducting currents and what its geometry is.
However, the simple idea which allowed to getting room-temperature superconductivity had been formulated several years ago. TI theory says directly about the existence of “topologically protected” 2-d states where the superconductivity should be reached. This is due to the full quantum interference of the scattered wave function.
The reason for this is that the 2d-carriers are spin-polarized: their momentum and spin are coupled (Figure 1). The strength of this coupling determines the operating temperature of topological insulators. This coupling is caused by spin-orbit-coupling (SOC), which may have very big value. This leads to a splitting of levels, and ultimately leads to the intersection of LUMO and HOMO in a Z = const-plane. One can observe linear dispersion in this point, which generates the so-called “Dirac cone”. Unlike graphene, its different parts are spin-polarized differently (Figure 2). Thus, one of the geometric dimensions acts as a tuning parameter for formation of a Z = const-plane, where zero bandgap and Dirac fermions do realize.
Spin polarization makes topological insulators much more perspective than graphene. The carrier mobility in graphene is high, but it is not a superconductor. However, absolute zero of the resistance of TI is still not experimentally proved, and maximal operating temperatures are still far from room temperature.
The maximal operating temperature of topological insulators is directly related with SOC value and mechanisms of its enhancement. We can proceed in two ways here. On the first, “classic” one, spin interacts with the magnetic orbital moment of the electron. Spin-orbit interaction is greatest for inner-shell electrons of heavy atoms. Therefore TI was originally created on the basis of heavy atoms and therefore this class of TI is the most studied class at the moment. But this way hasn’t leaded to high operating temperatures due to the fact that the SOC in this case is not high enough.
The second way is usage of intense internal electric fields. An electron moving in them is under action of an effective magnetic field. One of such fields is “Rashba effective field”. Rashba effect was mainly studied on quantum wells, and it was proved that SOC value can be giant in them. Strong electric field may exist both in
Figure 1. The scheme of quantum interference of the scattered wave function of spin-polarized 2d-particle. Spin is normal to momentum and is in its plane. There are two options of the scatter of defect which are shown by arrows. The resulting wave functions are mutually- opposite, so the aggregate wave function corresponding to the scattered state will be zero.
Figure 2. The formation of spin-polarized 2d Dirac fermions. SOC is increasing along Z-axis (on the left). SO-splitting of the levels leads to the intersection of LUMO and HOMO in a Z = const plane. In this plane the linear dispersion of 2d-carriers is observed which forms the so called “Dirac cone” (on the right). Its different parts are spin-polarized differently.
artificial superlattices and in molecules and complex crystals. For example, during carbon hydrogenation atoms of hydrogen are positively charged and generate local electric field. The effect of “giant SOC enhancement” (for 3 orders) during hydrogenation confirmed experimentally with graphene [4] . However let’s notice that graphene has minor intrinsic SOC.
Out of all carbon materials intrinsic SOC is maximal for nanotubes of the smallest diameter. A simple model is in charge here: a magnetic field of the rotating charge is inversely proportional to the radius of rotation. In the limit nanotubes of “zero” diameters have maximal SOC, and such “nanotubes” do exist. This is carbyne (Figure 3).
If we consider pure carbyne chain the calculations show that carbyne has maximal intrinsic SOC, which reaches 5 meV [5] . It is more difficult to determine the SOC close to hydrogenated end of chain. Various simulations have shown that the terminal hydrogen atoms are positively charged, but exact charge value is unknown. Basing on data about hydrogenated graphene we can assume that the enhancement also may reach 2 - 3 orders. In this case we get SOC around 1 eV close to the end of chain, what is much more than energy of the thermal oscillations at room temperature. This is more than enough to design room-temperature TI. However single chain is almost useless: initially having quasi-1d conductor, we get geometrically quasi-0-dimensional superconducting area on it. Way out of the difficulty is to use an ensemble of chains. But to assemble the proper “construction” at this level of scale is possible only with the help of self-assembling.
The experiments with carbon plasma in vacuum let to synthesize the stable form of carbyne―“oriented carbyne” [6] .
However, this material occurred to be so fantastic that Western science has ignored it. One of the reasons for this―it was unclear which forces are capable to hold the chain at the distance of 5 Å normal to the surface. Recent researches showed the presence of significant amount of hydrogen in this form [7] . Probably chains are held by dihydrogen interchain bonds. Another reason for skepticism is the complexity of the technique of vacuum self-assembling of oriented carbyne. It is interesting to note that the technique of alkyne self-assembling from the solution recently started to be under development. This process is so simple that easily can be repeated in every lab. At this moment there were obtained some samples which perfectly replicate the structure of ori- ented carbyne (Figure 4(c) taken from [8] ), but consisting of monolayer of alkynes. Presumably, the chains are held by adhesion to the surface and van der Waals forces. Self-assembling processes out of the liquid phase and out of the vacuum phase give the same geometry of crystal, what may indicate their same nature. The difference is in the periodic interchain crosslinking of long carbyne chains by transverse hydrogen layers.
Unfortunately, oriented carbyne was still synthesized by Russian scientists only. What is concerned belief in their results: besides numerous experiments international patents were obtained. The Raman-results, results from
Figure 3. The model of carbyne chain with terminal group H3. Blue balls―carbon atoms, red balls―hydrogen atoms. The outermost orbital shell is shown cylindrical for simplification. Electrons are under intense effective magnetic fields’ action close to positively charged terminal group H3.

Figure 4. The structure of oriented carbyne. (a) Scan in the atomic force microscope. (b) Supposed structure of carbyne close to the surface with dihydrogen bonds (big balls―carbon atoms, small ones―hydrogen atoms). (c) Self- assembling of the monolayer of alkynes out of liquid phase. STM-scan.
atomic force microscopes, by X-ray and electronic diffraction, mass-spectrometry cannot be attributed to anything else. However skeptics point out that according to multiple data single chains or their disordered massifs are unstable. This is really so, but it doesn’t give the right to assert that the oriented form is also unstable. Recent declarations [9] about that the stable phase of carbyne does not exist derive from lack of review of Russian researches.
2. Results and Discussion
The most interesting result of the studies of oriented carbyne is the effect of superinjection. Its essence is that the injection of charge carriers from oriented carbyne to any dielectrics (including electron emission to vacuum) occurs with equal efficiency [10] . This result can’t be explained in terms of classical band theory. The injection current has smooth current-voltage characteristic (CVC) starting almost from zero applied voltage. Therefore, carriers may obtain energy only from thermal oscillations of chains. For holes’ throwing to the valence band of SiO2 (?9.9 eV) typical barrier value is 6 eV. This high value is more than all thermal energy of oscillations of one short chain (around 20 atoms) at 300 K. So, the sequential stepped thermal activation on the set of chains over some energy ladder is required. But for classical carriers backward descending on energy ladder is much more probable than ascending. Pauli principle could prevent backward descending due to the complete filling of lower levels, but this process is associated with the accumulation of charge. The consequences of charge accumulation are the appearance of the electric field which prevents carriers’ movement and hysteresis on the CVC. Neither one nor the other was not detected in experiments. Another possibility could be related to the collective phonon process of simultaneous energy transmission, but this process is unknown. The consistent explanation of this effect was found in TI theory [11] . Presumably, the carriers are being activated on relativistic 2d Pseudo- Landau levels (PLL). This model is consistent with the other interesting result―with the spectrum of differential tunneling conductance [12] .
The main result of this research is shown in Figure 5. The interpretation of the authors is based on the model of ballistic conductance where the chain length comes into resonance with the wave function of an electron. Resonance peaks should be equidistant
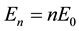 in this model. But it can be seen from Figure 5 that they aren’t. The similar nonequidistant resonance of tunneling current is observed in an stretched graphene. In case of graphene such spectrum presence is considered to be the main feature of PLL existence. We can also suppose that peaks are resonance with 2d PLL spectrum which has the form
in this model. But it can be seen from Figure 5 that they aren’t. The similar nonequidistant resonance of tunneling current is observed in an stretched graphene. In case of graphene such spectrum presence is considered to be the main feature of PLL existence. We can also suppose that peaks are resonance with 2d PLL spectrum which has the form
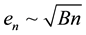 in case of oriented carbyne.
in case of oriented carbyne.
The reason for abnormal injection capability of oriented carbyne is that Dirac topologically-protected state takes place in it at room temperature. Pseudo-magnetic field generates PPL spectrum from it where each state is superconductive. Carriers in such states have increased lifetime even at the inversed population. Thus, the process of carriers’ ascending on energy ladder becomes possible and anomalous thermal population of the spectrum is realizing (Figure 6). Moreover, such spectrum is symmetric with respect to the charge sign, therefore the injection of holes occurs as easily as electrons.
The reason for the topologically-protected state appearance the giant Rashba effective field could be. When we turn to the reference frame moving with the electron, the electric fields produced by ionized nodes of crystal are acting like effective magnetic fields. In this case the electric field component along the Z-axis will appear only as an effective field in momentum space, and therefore it is unable to cause quantization. This is so called effective Rashba field (which also has Dresselhaus term), it is shown in Figure 7(a). It bends the energy bands depending on the spin direction, and if its value is sufficient in some Z = const plane, bands can overlap (Figure 2). In this plane which corresponds to zero bandgap the electron’s state is described by a wave function of spin- polarized Dirac fermion FD (Figure 7(b)).
The situation is radically different for the component of the electric field in the 2d-carriers’ plane. In this case
Figure 5. Spectra of differential tunneling conductance of oriented carbyne chains along chains. Chain length―50 nm (left) and 500 nm (right).
Figure 6. The superinjection process scheme. (a) The energy diagram of superinjection as consequent thermal activations on relativistic pseudo-Landau levels. (b) A top view of the injecting structure―the metal contact surrounded by carbyne. Carriers are sequentially activated on the cyclotron orbits of larger radii and finally injected downwards to the dielectric layer.
Figure 7. The micro-model of room-temperature superconductivity. (a) The appearance of effective Rashba field BRashba in momentum space while electron’s movement in an electric field directed along Z-axis. (b) The formation of Dirac fermion FD in some plane Z = const, whose spin is coupled to momentum. (c) The appearance of pseudo- magnetic field Bpseudo along Z-axis while movement of Dirac fermion in an electric field which is directed in its plane. (d) The resulting figure in geometric space, it takes into account both components of electric field; pseudo-Landau orbits of Dirac fermions.
effective magnetic field will appear along geometric Z-axis, and, therefore, could cause quantization (Figure 7(c)). This is so called pseudo-magnetic field. It appears in the stretched graphene as a result of the electric field of deformation nodes, and shows itself as the localization of conductivity by pseudo-Landau orbits. A similar process is possible and for such state of a topological insulator when the carriers are in the superconducting state of a spin-polarized Dirac fermion FD. Thus, superconductivity could turn from macroscopic to localized one by pseudo-Landau orbits (Figure 7(d)).
As can be seen, the Rashba SOC generating TI state appears to be related with pseudo-magnetic field. This relation follows from the geometric slope of the internal dipole relative to the plane of 2d-carrier. A similar relation exists in graphene with dopants [13] . Let’s note the extreme case: pure stretched graphene, where the electric field of the defect lies exactly in the 2d-carriers’ plane. In this case effective magnetic field will have only Z-component. Thus, graphene stretching leads to pseudo-Landau quantization, but does not impact on SOC. The other extreme case is «classical» low-temperature TI, where effective magnetic field doesn’t have Z-component and became apparent only in momentum space. Rashba field enhances SOC only, without localization of conductivity by pseudo-Landau orbits.
The origin of both effective magnetic fields is an internal electric field having T-symmetry. Thus, both of these effective fields are T-symmetrical unlike real magnetic field.
3. Conclusions
The simplified approach presented here requires further verification. Nevertheless, this theory shows us the direction of a conscious search for materials where room-temperature superconductivity can be implemented. First of all, these are self-assembled structures in a vacuum or in a liquid phase. The latter technique is very simple, and therefore has great potential. There are more and more results [14] , indicating that the monolayer of oriented molecules can influence the substrate radically. This is in agreement with our results, and indirectly confirms the presented model.
The theory according to which oriented carbyne is room-temperature topological insulator is also interesting in that it sheds light on the puzzle of HTSC. The localization of superconductivity occurs in oriented carbyne similar as it occurs both in pseudo-gap phase of HTSC and in “granular superconductivity”. According to the proposed model, it is nothing else than the pseudo-Landau quantization. Superconductivity “folds” by closed pseudo-Landau orbits. There may be only local effects inherent to superconductivity, but no macroscopic conductivity exists. It is known from experiments that the macroscopic superconductivity in HTSC can be achieved only at a certain level of doping, but in other cases there may be a phase of “local currents”. In the proposed model this becomes clear: a certain level of disorder is required to “break” the closed Landau orbits. If we apply HTSC phase diagram to oriented carbyne, then for turning it into a room-temperature superconductor we need to choose the proper dopant and its concentration.
References
- Hayward, L.E., et al. (2014) Science, 343, 1336-1339. http://dx.doi.org/10.1126/science.1246310
- Zhang, F., Kane, C.L. and Mele, E.J. (2013) Physical Review Letters, 111, 056402. http://dx.doi.org/10.1103/PhysRevLett.111.056402
- Esquinazi, P., et al. (2014) JETP Letters, 100, 336-339. http://dx.doi.org/10.1134/S0021364014170056
- Balakrishnan, J., et al. (2013) Nature Physics, 9, 284-287. http://dx.doi.org/10.1038/nphys2576
- D’yachkov, P.N. and Zaluev, V.A. (2014) The Journal of Physical Chemistry C, 118, 2799-2803. http://dx.doi.org/10.1021/jp410108f
- Kudryavtsev, Y.P., Evsykov, S.E., Babaev, V.G., et al. (1992) Carbon, 30, 213-221. http://dx.doi.org/10.1016/0008-6223(92)90082-8
- Prazdnikov, Y. (2012) Journal of Modern Physics, 3, 895-901. http://dx.doi.org/10.4236/jmp.2012.39117
- Zaba, T., et al. (2014) Journal of the American Chemical Society, 136, 11918-11921. http://dx.doi.org/10.1021/ja506647p
- Liu, M., et al. (2013) ACS Nano, 7, 10075-10082. http://dx.doi.org/10.1021/nn404177r
- Prazdnikov, Yu.E., Bozhko, A.D. and Novikov, N.D. (2005) Journal of Russian Laser Research, 26, 55-65. http://dx.doi.org/10.1007/s10946-005-0006-4
- Prazdnikov, Y. (2013) Journal of Modern Physics, 4, 994-999. http://dx.doi.org/10.4236/jmp.2013.47134
- Khvostov, V.V., et al. (2013) JETP Letters, 97, 205-208. http://dx.doi.org/10.1134/S0021364013040097
- Marcos, R.G., et al. Preprint arXiv:1409.8247.
- Jang, H.J., et al. (2014) ACS Nano, 8, 7192-7201. http://dx.doi.org/10.1021/nn502199z









