Received 16 October 2014; revised 12 November 2014; accepted 5 December 2014

ABSTRACT

The mechanical angular momentum and magnetic moment of the electron and proton spin have been calculated semiclassically with the aid of the uncertainty principle for energy and time. The spin effects of both kinds of the elementary particles can be expressed in terms of similar formulae. The quantization of the spin motion has been done on the basis of the old quantum theory. It gives a quantum number n = 1/2 as the index of the spin state acceptable for both the electron and proton particle. In effect of the spin existence the electron motion in the hydrogen atom can be represented as a drift motion accomplished in a combined electric and magnetic field. More than 18,000 spin oscillations accompany one drift circulation performed along the lowest orbit of the Bohr atom. The semiclassical theory developed in the paper has been applied to calculate the doublet separation of the experimentally well-examined D line entering the spectrum of the sodium atom. This separation is found to be much similar to that obtained according to the relativistic old quantum theory.

Keywords:

Spin Effect and Its Semiclassical Quantization, Electron and Proton Elementary Particles, Electron Drift in the Hydrogen Atom, Separation of the Doublet Spectral Lines

1. Introduction

In physics we look usually for general rules which govern the properties of a physical object, or a set of such objects. For example the Bohr atomic model gives a rather perfect description of several quantum parameters characterizing the hydrogen atom, but not the spin effects. The main items obtained from the Bohr description have been confirmed both on the experimental way, as well as on the quantum-mechanical footing which is considered to be a more flexible formalism than the old quantum theory. Simultaneously, however, quantum mechanics seemed to be enough complicated to give no transparent idea on the spin effects of the charged particles entering the atom. In consequence a treatment of the spin effects of the electron and proton was evi- dently absent in such simple model as the semiclassical Bohr approach to the hydrogen atom; see e.g. [1] . The aim of the present paper is to bridge this gap.

A general warning on the treatment of spin is that it should not be seeked as a result of the circulation effect of a particle about its own axis (see e.g. [2] ), and this view is shared also in the present approach. But instead of the motion about an axis which crosses the particle body, a charged particle may perform its spontaneous circulation in the magnetic field about an axis located outside the particle mass. The sense of such behaviour is―as we shall see―that in effect of the particle interaction with the magnetic field created by the particle motion, the particle energy becomes much lowered below the zero value of energy which can be assumed to be associated with the particle at rest.

In defining the position of the axis of the particle circulation in the magnetic field, the uncertainty relation for energy and time can be of use [3] - [5] . Beyond of time and energy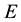, the principle contains also a reference to the particle mass 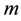and the speed of light:

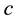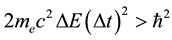. (1)

Evidently the rule (1) derived for electrons in [3] - [6] does apply to the particles which obey the Fermi statistics. But, for example, instead of electrons of the mass 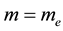considered in [3] - [6] , we can have also the gas of the proton particles of the mass distributed in the field of a negative background which makes the gas electrically neutral. A reasoning of [3] - [6] repeated in the case of an ensemble of the proton particles gives the result

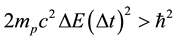. (2)

This makes (2) different from (1) solely by a replacement of in (1) by 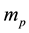in (2). Certainly and in (2) refer to the proton particle.

A consequence of the principle in (1) and (2) is a rule that two Fermi particles of the same kind cannot approach together to an arbitrarily small distance but they should be separated at least by the interval which―in view of (1)―is equal to [6]

(3)

for electrons, but becomes equal to

(4)

for the protons case; see e.g. [7] for the proton mass, spin angular momentum and spin magnetic moment.

The minimal distances (3) and (4) between particles represent respectively the Compton length of the electron and proton particle, on condition that the rationalized Planck constant is replaced by the original Planck constant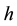. The kind of the formulae given in (3) and (4) has been derived before in [8] - [10] ; see also [11] .

In Section 2 we apply (3) and (4) to define the positions of the axes of a spontaneous particle circulation giving, respectively, the electron and the proton spin. Before these motions take place we assume that the particle energy of the electron and proton is at zero:

. (5)

2. Spinning Process of the Electron and Proton

A general law of physics is that any particle tends to assume a possibly lowest level of energy. In case of a charged particle this can be attained in effect of the particle circulation about some axis along which the particle motion induces the presence of the magnetic field. This situation implies that the kinetic energy of the orbital motion is associated with a particle. The axis of the motion can be located outside the extension area of the particle mass. As a distance of the axis from the particle location (for the electron and for proton) let us assume that (3) and (4) hold respectively in the electron and proton case.

The magnetic field causes the velocity along a circle normal to, and the balance of the forces requires that

(6)

where or, or, and or. In effect the force in (6) represents an equilibrium between the force of the field and the mechanical force due to the acceleration of a particle toward the track center (see e.g. [12] ). We postulate that

(7)

in the case of the electron particle, and

(8)

in the proton case.

The mechanical angular momenta of electron and proton become respectively

(9)

. (10)

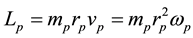
For the sake of simplicity the same size of charge for the electron and proton is assumed.

The and in (9) and (10) are the electron and proton circulation frequencies equal to

(11)

. (12)

The and are the strengths of the magnetic field suitable for the electron and proton case. For both kinds of particles we assume that the strength of is so large that electron or proton gyrate in the magnetic field with a speed close to. This requirement for the particle velocity is dictated by examination of the particle acceleration expressed in terms of the electric field and magnetic field [13] . In this case

. (13)

Evidently the acceleration (13) vanishes when the particle velocity becomes a constant. Thus we have

(14)

(15)

and

. (16)

With the aid of (3) and (4) we obtain from (14), (15) and (16):

(17)

and

(18)

on condition the absolute values of are taken into account. The orbital radii and [see (7) and (8)] substituted together with the velocities of (16) into the formulae (9) and (10) for the angular momentum give respectively

(19)

for the electron and

(20)

for the proton particle. In effect we have

. (21)

Evidently the formulae obtained in (19)-(21) do not depend on the particle mass. But a mass dependent parameter becomes the magnetic moment of a particle. For the electron case we obtain:

(22)

(which is the Bohr magneton) and for proton

(23)

called also the theoretical nuclear magneton applied in considering the nuclear particles [7] . The ratio between (23) and (22) is defined by

(24)

which is not very far from the ratio obtained from the experimental data for the magnetic moment of electron and proton [7] . In many cases the experiments performed on the nuclear magnetic momenta give the ratio not much different from where is the nuclear mass.

The energy of a spinning particle in the magnetic field is respectively represented by

(25)

for an electron, and by

(26)

for a proton. Therefore the gain of energy in the magnetic field due to formation of the particle spin is large. This gain of energy is expensed to provide the kinetic energy to a spinning particle having its velocity close to.

3. Magnetic Flux of a Spinning Particle, Conservation of Energy and Quantization of the Spin Motion

A parameter concerning spin which has its established experimental counterpart is the magnetic flux. Let us choose for an elementary planar area of that flux the circle

(27)

for electrons, and the circle

(28)

for protons. From (27), (28), as well as for the magnetic field strength taken respectively from (17) and (19), we obtain

(29)

and

(30)

respectively in the electron and proton case. An evident result is that

. (31)

Therefore the flux extended over the elementary areas in (27) and (28) does not depend on the particle kind represented by the particle mass. Moreover, the flux calculated in (29) and (30) is equal to a constant quantum term observed experimentally since a long time in superconductors [14] .

The time derivative of the flux term is zero, so we have the fundamental relation of electrodynamics

. (32)

Physically this means that a linear integral over representing the electric field along a circular path of the electron is equal to zero, therefore the energy of the circular motion in the magnetic field of is conserved.

Having the magnetic flux

(33)

the spin motion can be quantized according to a rule of the old quantum theory [12] [15] . It originates from a general rule given by Sommerfeld that momentum integrated over a closed path of the particle motion should be a multiple of the Planck constant:

(34)

here is usually considered as an integer number. But according to [12] Equation (34) can be transformed into

. (35)

By taking into account the first equation in (33) we obtain for (35) the relation

(36)

from which the spin quantum number becomes:

. (37)

This is a well-known result confirmed experimentally by the measurements on the gyromagnetic ratio in ferromagnets [16] performed a time before the spin discovery [17] .

4. Drift Velocity of a Spinning Electron in the Electric Field of the Proton Nucleus

Till the present time no other field than spontaneously created by a spinning particle has been considered. Now let us assume that the spinning electron meets the electrostatic field of the proton nucleus. A minimal dis- tance which can appear between the electron moving particle and the proton being at rest is defined in (3) be- cause (4) is too small to have a decisive influence. In this case

(38)

where is the absolute value of the electric field acting on the electron. Another force acting on the electron is where is the magnetic field intensity of the electron spin; see (17). Assuming that is normal to, the driving electron velocity obtained as a result of the joined action of both fields is [18]

. (39)

But it is easy to check from (17) and (38) that

(40)

is the fine-atomic-structure constant [2] [19] , so

. (41)

The result in (41) is precisely the electron velocity on the lowest orbit of the Bohr atom [1] . Therefore a combined action of the spin magnetic force of the electron and electrostatic force acting between electron and the proton nucleus, gives the speed of electron equal to that possessed on the lowest quantum state in the hy- drogen atom. The spin action of the proton on the electron spin moment present on the orbit has been neglected.

In effect the velocity along the lowest orbit of the Bohr’s hydrogen atom can be considered as a consequence of a drift motion being a result of superposition of many spinning rotations along very small orbits having their radii equal to (7) and travelled with a speed equal to. The time necessary to travel along the Bohr orbit having the well-known radius

(42)

is

(43)

whereas the travel time along the spin orbit calculated from (7) and (3) is equal to

. (44)

In consequence the number of spinning circular motions which take place in course of the electron drift along the first Bohr orbit is equal to

. (45)

This is a number independent of the mass. A diagram presenting schematically the motion of a spinning electron along the lowest Bohr orbit in the hydrogen atom is given in Figure 1. The circular frequency of a spinning electron is

. (46)

The mass has to be replaced by in case of a spinning proton frequency.

5. Semiclassical Approach to the Doublet Separation in the Sodium Atom

Experimentally the doublet separations in the spectra of atoms ascribed to the presence of the electron spin are

well known since a long time; see e.g. [20] . The problem is with a theoretical approach to these values. In the author’s opinion no satisfactory agreement between experiment and theory has been reported in this domain. Our aim is to calculate a doublet separation for the sodium atom in the case of the electron transition between two levels being on the same atomic shell but having different angular momenta:

(47)

[20] . The level energies are approached by the quantum-defect method. We follow first the idea developed by the old quantum theory, next the formalism of the present paper is applied.

The considered electron of the sodium atom is the valence electron moving outside the atomic core. The electron energy is given by the formula

. (48)

Here is the first Bohr orbit radius, and is an effective quantum number associated with the electron level by the quantum-defect formula

. (49)

We apply

(50)

for term and

(51)

for term; see Table 7.2 in [20] .

A difference of energy (48)

(52)

calculated respectively from (50) and (51) gives the length of the spectroscopic line equal to

(53)

which is not far from the experimental length

(54)

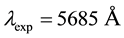
measured for the examined doublet [20] .

A proposal of calculating the doublet separation based on the relativistic old quantum theory applies the following formula for the change of energy connected with that separation [21] [22]

. (55)

Here

(56)

. (57)

For the effective nuclear charge equal to that applied before in (52), i.e.

(58)

moreover

(58a)

(58b)

we obtain

. (59)

A semiclassical approach of the present paper is based on the interaction energy of two magnetic dipoles. One of them is provided by the angular momentum of the electron circulating about the atomic core, another dipole is due to the electron spin. For the sake of simplicity we assume that the magnetic momenta of the orbital motion and the spin motion are either parallel, or antiparallel, in their mutual arrangement. For both cases the absolute value of the coupling energy is the same. On the level of type the electron has its angular momentum equal to, on the level of type let this momentum be. This leads to two orbital magnetic momenta on and equal respectively to

(60)

and

. (61)

We assume that momenta (60) and (61) are located at the nucleus. The absolute value of the spin magnetic moment (located at the electron position) is the same in both cases being equal to the Bohr magneton given in (22).

The electron in course of an excitation does not change its spin, but a separation distance between the magnetic momenta of the orbital motion and the spin momentum is changed. For state we have

(62)

and for state

. (63)

Therefore in case of a parallel arrangement of the orbital momentum and spin momentum the energy change of the momenta interaction due to the electron excitation becomes:

(64)

(the dot products of the vector joining the spin and orbital momenta with these momenta can be neglected be- cause the vector is assumed to be normal to the momenta).

The results obtained in (59) and (64) differ solely by a factor

. (65)

A substitution of the values, where is obtained in (59), in place of into a formula similar to (53) provides us with two wave lengths which differ by the interval equal to about

(66)

in the wave length calculated in (53) has been taken into account. The result (66) is smaller by the factor of about

(67)

than the experimental doublet separation equal to 6 angstroms [20] . A substitution of from (64) instead of (59) gives a similar separation to that obtained in (66); see (65).

6. A Look on the Dirac Theory and the Present Theory of the Electron Spin

A difference of both theoretical treatments of spin is evident. Dirac’s theory is essentially a relativistic quantum- mechanical approach to the electron motion; see e.g. [2] [19] [23] [24] . After the Hamiltonian of the problem is linearized, the four-dimensional matrices are applied as substitutions of the Hamiltonian operator. In the presence of an external electromagnetic field a simplification of the problem can be obtained by separating large and small components of the Dirac equation. In this way the spin-dependent interaction energy with the field can be calculated. The spin magnetic moment is coupled with the spin angular momentum by a constant term which is twice as large as in the classical electrodynamics. This implies that the spin quantum number should have the size of 1/2. Dirac’s electron particle considered in the field of the Coulomb potential gives rather complicated formulae for the electron wave functions which have no counterpart in the present semiclassical theory.

An advantage of the Dirac theory is that it gives an insight into antiparticles like positron, and presents an interval in the energy spectrum of particles and antiparticles of the size equal to. On the other side, no approach to the spin and magnetic moment of such particles like protons has been explicitly outlined by Dirac.

The theory of the present paper is much different than the Dirac approach. First the method is essentially of a semiclassical nature since no wave functions are considered. A basic reference to the quantum theory is the uncertainty principle applied to the changes of energy and time; see (1) and (2). The term

(68)

included in the formalism is obtained in effect of the derivation procedure of the principle; see [3] - [5] . A further analysis of the change of a free-particle energy entering the principle gives a minimal distance for the geometrical separation between the particles; see [6] . This separation allowed us to make a proposal of the spin as a result of a spontaneous circulation of the electron, or proton, performed about an axis located outside the particle mass; see Section 2.

Another advantage of the present theory is that both Fermi particles―electron and proton―can be considered on an equal footing because of the fermion character of these particles; see (1) and (2) which differ solely in their mass symbol. This allowed us to obtain an insight into the spin and magnetic moment of protons together with similar electron properties. The theoretical results obtained for both kinds of the particles are confirmed by the experimental data to a large degree.

Moreover, the Dirac theory assumes that certain magnetic field should be present in order to obtain a spinning electron particle, but the size of such field is not defined. In the present approach the size and source of the magnetic field acting on the particles are the results of the theory.

7. Summary

A semiclassical model of two spinning charged particles (electron and proton) has been proposed on the basis of a quantum uncertainty principle for energy and time and the classical electromagnetic theory. The main reason of a spontaneous formation of a spinning particle is a strong lowering of the particle energy in the magnetic field associated with the existence of the spin circulation.

The mechanical angular momentum connected with the spin is found to be the same for electron and proton, and the mass difference between the particles becomes sound only for the magnetic spin moment. This very fact is confirmed by experiment (see e.g. [7] ) which provides us with the ratio of the magnetic moments similar to that obtained by the present theory.

It could be noted that the mechanical moment of a proton equal to that of a spinning electron seemed to surprise many physicists since a long time; see e.g. [25] . This kind of feeling is stimulated by the fact that the magnetic moment of proton is about times smaller than that of electron. The independence of the mechanical spin momenta of both particles on their mass can be explained by a reference to the fact that the particles obey the same (Fermi) statistics and have the same absolute value of the electric charge. Therefore the uncertainty principle for energy and time applied to electrons and protons is different just in the mass value; see (1) and (2). But the orbit radius of each of these spinning particles is inversely proportional to their mass. Since the angular momentum is by definition proportional to the mass, the both mass expressions cancel together in the angular momentum formula which becomes independent of the mass size.

When a spinning electron meets the electrostatic field of a proton, it can be demonstrated that the resulted drift velocity of the electron becomes equal to the velocity of that particle on the lowest quantum level of the Bohr model of the hydrogen atom.

The effect of the spectral doublet separation has been also examined for the atomic sodium taken as an example. A semiclassical calculation of the present paper gives almost the same result as it is provided by the relativistic old quantum theory.

References