Journal of Modern Physics
Vol.06 No.01(2015), Article ID:53421,8 pages
10.4236/jmp.2015.61006
Neutron Back- and Front-Face Bragg Diffraction on a Thin Si Single Crystal Excited by Ultrasound
E. Raitman1, V. Gavrilov1, D. Mjasischev1, Ju. Ekmanis1, A. Hoser2, T. Hoffmann2
1Institute of Physical Energetics, Riga, Latvia
2Helmholtz-Zentrum, BENSC, Berlin, Germany
Email: eraitmans@apollo.lv
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 28 December 2014; accepted 18 January 2015; published 21 January 2015
ABSTRACT
In this research project, we measured and analyzed the spatial distribution of neutron beam Bragg diffracted from the front- and back-faces of thin Si single crystal undergoing on ultrasound excitation. For the perfect crystal, it is shown that when the acoustic wave amplitude is increased, the front-face peak position remains unchanged and its value grows linearly. The values of ultrasound wave amplitude were determined. The back-face peak becomes asymmetric and tends to disappear. New types of Pendellösung fringes in the center of the diffraction profiles were observed at the first time. It is supposed that in the perfect crystal this effect may be due to the appearance of the new “sonic” extinction length, depending on the amplitude of the ultrasonic wave. Thus, it leads to the new interference interactions between neutron wave and ultrasonic phonons. It is established that within the framework of the dynamical theory of the neutron scattering, some asymptotic models valid for the case of Laue geometry as well as Kato’s quasi-classical approximation can be applied in the case of Bragg geometry also. Good agreement between experimental data and the theory has been obtained.
Keywords:
Neutron Diffraction, Ultrasound, Pendellösung

1. Introduction
Experiments that confirmed the correctness of theoretical considerations based on the dynamical theory of wave radiation fields in the interior of a perfect crystal were performed by Kato [1] -[3] for X-ray and later by Shull [4] [5] for diffraction of silicon and germanium single crystals with neutrons. In [4] [5] studying neutron wave front-face, back-face and end-face scattering in a thick perfect Si and Ge crystals, Bragg reflections profiles were measured by scanning with a very narrow analyzing slit across the diffracted beam. In these experiments, the sample was not moved while the slit was scanned across the outgoing beam. The spatial profiles of reflections from the front and back crystal faces were described by the dynamical theory for neutron scattering [5] - [8] . It was shown that the interior volume of the perfect crystal does not contribute to the reflections, except some additional intensity due to weak diffuse scattering. The description based on the theory of dynamical diffraction considers the wave pattern propagating in the periodic potential of an ideal lattice, and a variety of features is explained. One of the most important effects of dynamical diffraction is the strongly limited intensity diffracted by an ideal crystal in Bragg position. The interference effects from the wave fields causing the almost zero intensity diffraction disappear very quickly if the translation symmetry in a perfect crystal is violated due to any disturbance, such as static deformation strain or the ultrasonic waves. In the both cases Bragg-reflected intensity increases. For example, in [9] [10] it was shown that back-face Bragg diffraction is very sensitive to the ultra- small static deformation strain.
The ultrasound (US) influence on the neutron and X-ray Bragg diffraction has been investigated much less than in the Laue case, probably because of its complicated theoretical description, in spite of the fact that most of the monochromators installed on the neutron and X-ray spectrometers operate in Bragg’s scattering geometry. Recently it was shown [11] that in a thick Ge single crystal undergoing US excitation the Bragg back-face peak becomes asymmetric and tends to disappear. Such a back-face scattering was observed for the first time and successfully described within frameworks of the modified dynamic theory of neutron scattering.
Present work should be considered as a continuation of Schull’s experiments at a modern level (position- sensitive detectors (PSD) and no the narrow analyzing slit , more powerful neutron flux, another technique for measuring Bragg profiles, etc.). However, in contrast to the mentioned Schull’s works our experiments were carried out with “good” neutrons (monochromatic) and a “spoiled” by ultrasound perfect crystal instead of Shull’s “bad” neutrons (a white beam with high collimation) and perfect crystals.
The purpose of this paper is to present new experimental data of the study and the neutron interactions with acoustic waves (AW) of rather small amplitude observed using the Bragg’s diffraction method from perfect thin Si single crystal. Fundamental issues such as investigation of the diffraction process itself as a simultaneous response to the ultrasonic field as well as its applications to the beam optics or materials research are also concerned. Particular attention is paid to a spatial Pendellössung of the neutron intensities observed inside Bragg profile.
2. Experimental Details
Neutron diffraction measurements were carried out with an HZB BENSC E6 Diffractometer [12] . It is equipped with a horizontally and vertically bent monochromator. This latter consists of 105 pyrolytic graphite crystals (20 × 20 × 2 mm3) mounted on a 15 × 7 matrix leading to a relatively high flux at the sample position. In combination with a position sensitive detector and variable in-pile collimation, it is mainly used to study magnetic materials. Measurements can be carried out on both single crystals and powders. As opposed to a conventional diffractometer (small divergence, large beam cross section, flat monochromator) the focusing diffractometer uses a horizontally and vertically bent monochromator in combination with a fan collimator imitating a vertical slit with varying distance from the monochromator. By varying the horizontal bending of the monochromator and the fan opening of the in-pile collimator, a correlation between the direction of the incoming neutron and its wavelength can be achieved. Thus, the orientation of the resolution ellipsoid can be changed with respect to the scattering vector H. In the focusing configuration, the resolution ellipsoid is oriented with its long axis perpendicular to H, so the resolution parallel to H is maximized. This mode yields an increase in neutron flux at the sample position of a factor 2 maintaining the good resolution.
The scheme of experiment is shown in Figure 1.
In our experiments a dislocation-free silicon single crystal with dimensions 14 × 4 × 0.4 cm3 (111-reflection) was used as a sample. A monochromatic and well-collimated neutron beam with λn = 0.243 nm and a cross section of 1 × 10 mm2 was directed to the sample. The samples quality was checked preliminary with DC X-ray
Figure 1. The layout of the experiment. M―monochromator; S is a slit forming neutron beam; PT is piezo transducer for transverse AW creation; PSD―position sensitive detector; FFS―front face scattering; BFS―back face scattering; H is reciprocal lattice vector; ks is ultrasound wave vector. Nuclei displacement u in a standing AW is u = wcos(νst)cos(ksx), where w is an AW amplitude, νs is AW frequency, u is parallel to H. The circle in the diagram shows the direction of transverse acoustic wave propagation (ks). ks is perpendicular to H. T is the samples thickness, T = 4 mm.
diffractometer and the FWHM of the rocking curve was 3.1 arc.sec , close to the theoretical expectation. Different to the experiments mentioned above an analyzing slit was not used. Instead, the spatial distribution of the reflected neutron beam was measured with a position sensitive detector. After finding the optimal relation ΘB - 2ΘB, where ΘB is Bragg’s angle the sample remained unmoved and the distribution of the reflected intensity was measured rotating PSD with an angular step of 0.1 degree. This procedure in general is similar to the scanning by slit method, however, allows a much faster data acquisition.
Transverse acoustic waves excitation was realized using LiNbO3 piezo transducer with the frequency νs = 42.3 MHz. The AW propagated perpendicular to the scattering vector (ks ^ H). In all cases the amplitude w of the polarized AW was parallel to the vector H. Piezo transducer was glued to the sample by salol.
Besides of direct measuring the diffraction intensity 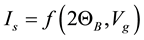 where Vg is the rf generators voltage the actual diffraction profile can be obtained also in the form of relative intensity changes η:
where Vg is the rf generators voltage the actual diffraction profile can be obtained also in the form of relative intensity changes η:
 (1)
(1)
Is and I0 are diffraction intensity when ultrasound is switched on and off, accordingly for each profile point x, i.e. throughout the whole angular range  with
with 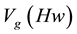 as a parameter, where
as a parameter, where
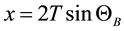 (2)
(2)
T is the sample thickness.
3. Main Results and Discussion
It was shown recently [11] that for thick crystal at the same time with the main Bragg’s peak increasing, acoustic wave amplitude growing, and the back-face peak become asymmetric and tend to disappearance as the peak.
The common situation becomes more complicated for the thin crystal if we analyze the effect of ultrasound on the spatial diffraction intensity distribution between the FFS and the BFS reflection peaks shown on the Figure 2(a), Figure 2(b).
Thus, total diffraction intensity Is for FFS grows with the increasing of AW amplitude w(Vg) but its position in 2Θ-space remains essentially unchanged and independent of Vg value. At the same time, BFS peak shifts to the profile middle. This result coincides with those obtained previously in [11] for thick Ge single crystal. But Figure 2(a), Figure 2(b) demonstrate not only a smooth intensity growth of the FFS peak and BFS peak shift to the profile centre, but also the presence of spatial intensities oscillations in the crystal inside and common broadening of intensity spatial profiles with Vg increasing.
Interference nature of the interaction between the reflected neutron-beam and the acoustic waves is becoming more evident from Figures 3(a)-(d).
From Figure 3(a), Figure 3(b) it is evident that FFS peak at 2ΘB = 46.29 deg. has invariable position for all Vg. With US wave amplitude increasing, the relative gain η varies linearly (with accuracy up to 1%) as well as the total intensity is. This fact will be used below for calibration the voltage on the piezo transducer Vg in units of the AW amplitude w.
If absorption does not occur (as it is for Si crystal), the diffracted beam intensity Is in the approximation of an incident spherical monochromatic wave at US switched on is [13] :
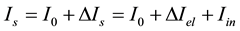 (3)
(3)
with
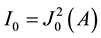 (4)
(4)
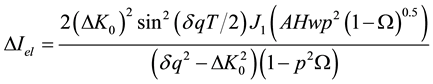 (5)
(5)
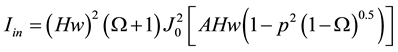 (6)
(6)
where 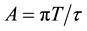 is the reduced crystal thickness;
is the reduced crystal thickness; 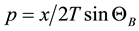 is a dimensionless parameter that is proportional to the coordinate x, reckoned within the scattering face of the crystal from the point of incidence of the neutron beam (x = 0 for FSS peak),
is a dimensionless parameter that is proportional to the coordinate x, reckoned within the scattering face of the crystal from the point of incidence of the neutron beam (x = 0 for FSS peak),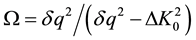 ;
; 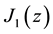 and
and 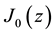 is a Bessel function of the first and zeroth order,
is a Bessel function of the first and zeroth order, 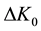 is the gap between the sheets of dispersion surface and
is the gap between the sheets of dispersion surface and 

Figure 2. Diffraction intensity dependence on rotation angle 2ΘB and voltage Vg on PT. (a) the general view of the diffraction profile changes; (b) the total diffraction intensities distribution vs the generator voltage. 1―Vg = 0 V, 2―Vg = 2 V, 3―Vg = 5V, 4―Vg = 8 V.
Figure 3. Changes of the diffraction intensity Is (a) and parameter η (b)-(d) as a function of 2ΘB and Vg (Hw): (a) intensity for FFS reflection at fixed 2ΘB = 46.29 deg. vs Vg; (b) the same as (a) for parameter η. The lower scale in Figure 3(b) is the calibrated values Vg according to expression (8) (see below); (c) η angular dependence in the whole 2ΘB range. Vg is parameters: 1―0.5 V, 2―2 V, 3―3 V, 4―6 V, and 5―8 V; (d) η dependence on Vg for two peaks: 1―2ΘB = 45.35 deg. and 2―2ΘB = 46.1 deg. Solid curves in Figure 3c and d are fitting by means of Bessel’s functions of the first order.
Taking into account that at 





where c is normalization constant, supposing HW = cVg. Expressions (7,8) describe very well experimental data. From (8) and Figure 3(c) it follows that AW amplitude w = 0.042 nm/1V.
Depending on the AW frequency, a distinction can be made between two different physical mechanisms of US influence on neutron and X-ray diffraction. At AW frequency νs < νres where νres is the frequency at neutron- (X-ray-) acoustic resonance condition (see below), the dispersion surface (DS) varies insignificantly and the problem is solved in terms of the usual perturbation theory [15] [16] . The eigen function corrections are of the order of Hw and additions to the scattering intensity are of the order of (Hw)2. Hence, at sound frequencies νs < νres there takes place nearly complete “pumping” of the elastic component of scattering intensities into inelastic one. The Mossbauer diffraction spectra obtained on single Si crystal confirm the theoretical results [17] .
Effect of ultrasound on the DS in a perfect crystal in the Bragg geometry is schematically shown in Figure 4.
The US phonon’s absorption (emission) by neutron mixes Bloch states and displaces the DS of the neutron quasi-pulse δq:

where θB and vn are the Bragg angle and the neutron velocity, respectively. Since the second term in (9) is much lower than the first one, expression (9) is valid for AW frequencies used in our experiments. A condition of the neutron-acoustic resonance, i.e. when sheets of the dispersion surface touch one another mutually, and

τ is the extinction length. Expressions (9,10) are valid if H ^ ks, and this corresponds to the conditions of transversal AW in our experiments. The expressions (10) differ from those for the case of X-ray acoustic resonance [18] because the neutrons with a wavelength 0.243 nm have the speed comparable with the speed of ultrasound phonons and between them there is an exchange of energy [14] .
Since US effectively changes the initial dispersion surface due to the creation of new energy gap δq on the dispersion surface 

τ is the extinction length for non-excited crystal.
Thus, US increase the depth of neutron penetration in the crystal interior without significant attenuation of the incident beam intensity in the all Hw range.
Note that the result similar to given by (10,11) can be obtained using the Kato quasi-classical approximation [2] [7] [8] . To this a simple procedure leads―that of replacing (in terms of the original theory) the initial extinction length τ0 with “sonic” τs. Indeed, according to this theory the distribution of the diffracted-beam intensity at front-face scattering in the approximation of an incident spherical monochromatic wave is:

where A and p are defined above and by making use of the asymptotic expansion of Bessel function for 

where f is numerical constant. Expression (13), up to numerical factors, coincides with expression (7)―that is, correctly describes the linear growth of FFS peak with increasing US wave amplitude. However, the absence of an exact theory does not allow for quantitative description of the features shown in Figure 3(c) and Figure 3(d),
Figure 4. Schematic sketch of the dispersion surfaces for Bragg’s geometry in the presence of US excitation; n is the normal to the surface, ks is AW wave number, δq is neutron quasi-pulse, ΔK0 is the gap between the sheets of dispersion surface when US is switched off. The case of transverse AW.
the appearance of two peaks of η (Figure 3(c)) and its oscillatory dependence on 2ΘB and Vg (Figure 3(d)). Moreover, the shift of BFS peak towards the center of the profile cannot be explained satisfactorily.
The Kato quasi-classical approximation based on the fact that the effect of total reflection is due to the wave field in a crystal undergoes an exponential decrease, which leads to a conversion of the incident wave into diffracted one. This occurs at a depth of about extinction length τ. However, this theory cannot be used in the case of violation of the translational symmetry caused by ultrasonic disturbance of the crystal lattice. Therefore, in principle, description of the changes in FFS extinction peak intensity is not applicable with this approximation without some modifications of diffraction profile under the US influence.
In the framework of dynamical theory, one may explain the diffraction profile broadening by the creation of ultrasound induced satellites, which are very close spaced and unresolved The sharp increase in the relative intensity at the centre of profile (2ΘB = 46.09 deg.) and near the BFS peak (2ΘB = 45.4 deg.) (Figure 3(c)) may be connected with the radiation channeling effect under the US influence [20] or with multifold neutron scattering. However, these assumptions do not explain the Pendellösung pattern.
Expressions (3)-(6) are valid in the case of symmetric Laue’s diffraction and qualitatively give correct description of the results obtained, but a quantitative comparison of the experimental data with the theory is unsatisfactory. This is not surprising, since the diffraction experiment was carried out for Bragg’s case. For example, the experimental results are better approximated by function 2J1(2ΘB, Hw) rather than by the zero-order Bessel function.
The oscillatory dependence shown in Figure 3(c), Figure 3(d) can be explained by the interaction of transmitted and reflected neutron waves at new extinction length τs and could be successfully described with the new theory of the spatial distribution of a spherical neutron wave propagating through a crystal that has been excited by US.
4. Conclusion and Summary
Because the back-face scattering, spatial diffraction profiles I0 = f(2ΘB) without US have a usual two-peak shape but it differs from the case of the thick crystal. Ultrasonic waves create well-known disturbance of the dispersion surface owing to which the intensities of front-face peaks increase linearly due to the appearance of additional contribution to Bragg’s reflections from the satellites, but with increasing amplitude of the US wave, position of the extinction peak (FFS) in the 2ΘB―space remains unchanged. This fact allowed us to estimate the AW amplitude using expressions (7, 8) for the spatial profiles of diffracted neutron beams.
The spatial distribution of the diffracted beam at “no sound” and linear growth of the FFS extinction peak intensity when sound is switched on can be described also in terms of the quasi-classical Kato’s approximation, introducing a new extinction length whose value depends on the AW amplitude. This result―up to a numerical factor―coincides with that obtained using expressions (8-11), taking into account the inelastic scattering of neutrons. However, when US is switched on, the neutron scattering inside a crystal has more complicated behavior and cannot be satisfactorily explained only by the appearance of a new “sonic” extinction length [21] . Pendellösung fringes appear, clearly manifested at measuring the relative changes in the diffraction intensity at each point of profile η = f(2ΘB). New interference fringes are observed near the FFS and BFS peaks, the intensity of which increases with increasing AW amplitude. They are well described by Bessel’s function of the first order (Figure 3(c), Figure 3(d)).
Note that detailed measurements of diffraction profiles under US excitation have not been taken even in perfect crystals, and definitely not in strained ones. Thus, our results could be considered as useful for theoreticians in creating the exact theory of Bragg scattering of neutrons under the ultrasound.
The data obtained may also be used, in principle, in the devices governed by ultrasound for the neutron beam monochromatisation (see, e.g. [22] ).
References
- Kato, N. (1969) Acta Crystallographica, A25, 119. http://dx.doi.org/10.1107/S0567739469000192
- Kato, N. and Ando, Y. (1966) Journal of the Physical Society of Japan, 21, 964. http://dx.doi.org/10.1143/JPSJ.21.964
- Kato, N. and Lang, R. (1959) Acta Crystallographica, 12, 787. http://dx.doi.org/10.1107/S0365110X59002262
- Shull, C.G. (1968) Physical Review Letters, 21, 1585. http://dx.doi.org/10.1103/PhysRevLett.21.1585
- Shull, C.G. (1973) Journal of Applied Crystallography, 6, 57.
- Leilinder, A., Shull, C.G., Arthur, J. and Horn, M.A. (1983) Physical Review A, 28, 487. http://dx.doi.org/10.1103/PhysRevA.28.487
- Rauch, H. and Petrashek, D. (1978) Dynamical Neutron Diffraction and Its Application. In: Dachs, H., Ed., Topics in Current Physics, Springer-Verlag, Berlin - Heidelberg - New York, 6, 303-351.
- Abov, Yu.G., Elyutin, N.O., et al. (2002) Physics of Atomic Nuclei, 65, 1933.
- Agamalian, M., Iolin, E., Rusevich, L., et al. (1998) Physical Review Letters, 81, 602.
- Agamalian, M., Triolo, R. and Wignall, G.D. (1998) Journal of Applied Crystallography, 31, 35. http://dx.doi.org/10.1107/S0021889897014581
- Raitman, E., Gavrilov, V., Mjasischev, D., Hoser, A., Stusser, N. and Arulraj, A. (2010) Nuclear Instruments and Methods in Physics Research Section B, 268, 3411-3414. http://dx.doi.org/10.1016/j.nimb.2010.08.004
- Stusser, N. and Hofmann, M. (2002) Nuclear Instruments and Methods in Physics Research Section A, 482,744-751. http://dx.doi.org/10.1016/S0168-9002(01)01681-3
- Iolin, E. and Entin, I. (1983) Journal of Experimental and Theoretical Physics (JETP), 85, 1692-1694.
- Iolin, E., Farago, B., Mezei, F., Raitman, E. and Rusevich, L. (1998) Physica B, 243-245, 1213-1215.
- Mikula, P., Lucas, P. and Kulda, J. (1992) Acta Crystallographica Section A, 48, 72-73. http://dx.doi.org/10.1107/S010876739100627X
- Blagov, А., Коvalchuk, М. and Коhn, V. (2006) Crystallography, 51, 146-149.
- Gavrilov, V.N., Zolotoyabko, E.V. and Iolin, E.M. (1990) Hyperfine Interactions, 58, 2427-2432. http://dx.doi.org/10.1007/BF02398355
- Entin, I.R. (1977) Journal of Experimental and Theoretical Physics Letters, 50, 269-272.
- Iolin, E., Raitman, E., Kuvaldin, B. and Zolotoyabko, E. (1986) Journal of Experimental and Theoretical Physics (JETP), 66, 218-227.
- Entin, I.R. and Puchkova, I.L. (1984) Soviet Solid State Physics, 26, 1995-1999.
- Raitman, E., Gavrilov, V., Mjasischev, D. and Brezgunov, M. (2009) Journal of Surface Investigation. X-Ray, Synchrotron and Neutron Techniques, 3, 902-907. http://dx.doi.org/10.1134/S1027451009060093
- Guigay, J.P., Mikula, P., Hock, R., Baruchel, J. and Waintal, A. (1990) Acta Crystallographica Section A, 46, 821-826. http://dx.doi.org/10.1107/S0108767390005517
Nomenclature of Abbreviations
A = πT/τ―reduced thickness of the sample
AW―acoustic wave
c,f―the fitting constants
DS―dispersion surface
BFS―back-face scattering
FFS―front-face scattering
H―vector of reciprocal lattice
Is,I0―diffraction intensity when US is switched on and off, respectively
IFFS―front-face diffraction intensity
Iel,Iin―intensity of elastic and inelastic scattering, respectively
J0,J1―Bessel function of the zero and first order
ΔK0―gap between DS sheets
ks is US wave vector
δq―neutron quasi-pulse
n―the normal to the scattering surface
p―a dimensionless parameter proportional to the coordinate x
T―sample thickness
US―ultrasound
u―nuclei displacement in a standing AW
Vg―generator voltage
vn―neutron velocity
w―an AW amplitude
x―coordinate
ΘB―Bragg’s angle
η―relative diffraction intensity
νs―AWfrequence
τ, τs―the extinction length when US is switched off and on, respectively




