Journal of Modern Physics
Vol.5 No.8(2014), Article ID:46399,10 pages DOI:10.4236/jmp.2014.58072
Spectra of Plasmon Polaritons at Metal―Insulator Interfaces of a Nanosized Gold Film: Expansion into Components and Their Systematization
Lidiya Maksimenko, Igor Matyash, Oleg Mischuk, Svetlana Rudenko, Boris Serdega, Maksim Stetsenko
V. Lashkaryov Institute of Semiconductor Physics, NAS of Ukraine, Kyiv, Ukraine
Email: bserdega@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 11 February 2014; revised 8 March 2014; accepted 5 April 2014
ABSTRACT
The spectral characteristics of surface plasmon resonance (SPR) in nanosized gold films were studied with method of internal reflection in the Kretschmann geometry. Using modulation polarimetry technique, we measured the spectral and angular characteristics of the parameter . The latter is a physical difference between the reflection coefficients R of linearly polarized lights whose wave field azimuths are perpendicular
. The latter is a physical difference between the reflection coefficients R of linearly polarized lights whose wave field azimuths are perpendicular 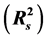 and parallel
and parallel  to the plane of incidence. An asymmetry of spectral profile of the parameter
to the plane of incidence. An asymmetry of spectral profile of the parameter 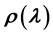 was found. It depends on the angle of light incidence and indicates complex composition of the reflection coefficients. A procedure for determination of normalized quantity
was found. It depends on the angle of light incidence and indicates complex composition of the reflection coefficients. A procedure for determination of normalized quantity 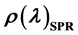 in the SPR spectra is proposed, and their expansion into components is made using that procedure. A possibility of adequate approximation of the
in the SPR spectra is proposed, and their expansion into components is made using that procedure. A possibility of adequate approximation of the 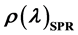 spectra by the Gauss functions with no less than three components (differing in frequency and amplitude) is shown. The resonance parameters are determined and used for construction of dispersion curves
spectra by the Gauss functions with no less than three components (differing in frequency and amplitude) is shown. The resonance parameters are determined and used for construction of dispersion curves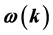 . Their interpretation is given based on the theoretical model for waveguide modes on both metal film surfaces that were proposed earlier.
. Their interpretation is given based on the theoretical model for waveguide modes on both metal film surfaces that were proposed earlier.
Keywords:Surface Plasmon Resonance, Gold Films, Modulation Polarimetry

1. Introduction
The surface plasmon-polariton (SPP) waves excited at interfaces of metal-insulator structures were and still remain an object of keen interest of physicists, both theoreticians and experimentalists. Since the appearance of one of the first publications on that subject [1] , a lot of results in the area have been obtained. Some of them are discussed in monographs [2] -[4] .
In the course of further investigations of plasmon-polaritons, the trend of approaches and techniques drifted mainly from plasma methods [5] [6] to waveguide concepts. Numerous results on polariton waveguide modes are concentrated in recent review [7] . They are mostly theoretical. In [8] , it was shown that SPPs excited at the interface of a nanosized metal layer can propagate over macroscopic distances. In this case, the dispersion curve w(kх) for polariton waves propagating at the interface between two semi-infinite media has (as follows from [9] - [11] ) a single branch, i.e., there is one-to-one correspondence between the values of wave vector kх and frequency ω.
A classical waveguide structure is a metal film placed between two dielectric materials with the same permitivity. Two different modes can be excited in such symmetric structure [12] [13] . In another, more widespread asymmetric limiting case, a film of finite thickness is limited on both sides by media with different refractive indices. Now the dispersion relation w(kx) for SPP waves propagating through thin metal films falls into two ones. This fact served in the review [7] (as well as in further works [14] -[16] ) as a reason for coinage of the terms long-range and short-range polaritons related to the wave attenuation length in asymmetric insulator-metal-insulator structures. According to [17] , the dielectric properties of waveguides are determined by the effective complex refractive index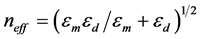 , where
, where 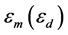 is metal (insulator) permittivity.
is metal (insulator) permittivity.
One of the ways for excitation of SPP waves is application of the Kretschmann-Raether geometry [5] ―one of the versions of widely used optical scheme. Its design involves a totally reflecting prism (semicylinder) with a metal film on its reflecting surface. Usually such a structure is formally considered as a three-layer structure involving glass, metal and air. One can see that it is characterized by asymmetry of dielectric properties of the materials neighboring on both sides of the metal film.
This feature, according to the above expression, is a formal reason for appearance of asymmetry of waveguide spectral characteristics. Their physical manifestation is observed under oblique incidence of light onto a totally reflecting prism where polaritons may be excited at the metal-insulator interfaces. To illustrate, most of light energy (long-range mode) is concentrated in a waveguide with lower efficient value of refractive index (metalair interface). The short-range mode (with lower energy) is concentrated near the interface between metal and insulator with higher refractive index, i.e., at the inner film surface [18] .
In a number of further works [19] -[21] such an approach found further development in SPP characterization. It gives, in particular, that the short-range polariton mode is localized at the inner surface of metal film. It was also noted that the short-range mode has two states, namely, symmetric (s-mode) and antisymmetric (α-mode). The electric field of the α-mode has inverse phase. However, the main illustration of the noted properties of waveguide modes is their dispersion characteristic. Just this result was theoretically obtained for an Ag film 10 nm thick in [22] as three ω(k) curves spaced in frequency and presenting two modes, one of them having two states, one of them having two mentioned states.
We know the only work [23] with experimental results illustrating the above-mentioned theoretical calculations. Indeed, in that work the luminescence enhanced by polariton resonance was studied and pronounced contour asymmetry in its spectra was found. Moreover, it was shown that, as the angle of incidence of light on the prism changes, the above asymmetry undergoes mirror inversion relative to the symmetric contour observed at the angle of incidence of 52.2˚. Evidently the asymmetry of those spectra contains data on the components of SPP waveguide modes. However, the characteristics presented in [23] are superposition of two effects, namely, luminescence and SPP. This excludes the possibility of obtaining from them information for building the dispersion characteristics w(k) of waveguide modes. Moreover, correct analysis of SPR spectra is possible only within the normalized1 (as expressed in [24] part of resonance energy transfer that depends), in its turn, on some physical parameters.
Therefore, the aim of the present work (determination of dispersion characteristics w(k) of SPP waveguide modes built on the results of expansion of experimental spectra into components, with subtraction of non-resonance component) seems logical. It should be added that the resonance part of light can be obtained from the angular dependences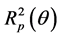 , in which (according to [24] ) it has specific values. Indeed, transfer of them from the characteristics
, in which (according to [24] ) it has specific values. Indeed, transfer of them from the characteristics 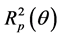 (measured at different wavelengths with sufficient discreteness) to the spectra
(measured at different wavelengths with sufficient discreteness) to the spectra 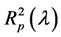 would give solution (although awkward) of the above problem.
would give solution (although awkward) of the above problem.
There exists, however, another way, namely, determination of the non-resonance component (that is much smaller) and subtraction of it from the spectral dependence. There are some reasons to consider that way more exact and so preferable. A substantial reason for this is application of the measuring analytical procedure based on modulation of electromagnetic radiation polarization―the so-called polarization modulation (PM) technique. Its advantage for investigation of SPR was demonstrated in our work [25] and later in a number of works generalized in [26] .
In the present work, we demonstrate further development of information ability of the PM technique by the example of investigation of uniform nanosized Au films with thickness optimal for SPR demonstration. We mean spectral analysis of characteristics of the parameter ―polarization difference between the internal reflection coefficients of linearly polarized light with wave field azimuths perpendicular
―polarization difference between the internal reflection coefficients of linearly polarized light with wave field azimuths perpendicular 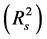 and parallel
and parallel 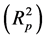 to the plane of incidence. It was shown in [27] that expansion of spectrum into components of Gauss normal distribution is useful.
to the plane of incidence. It was shown in [27] that expansion of spectrum into components of Gauss normal distribution is useful.
2. Experimental Setup
The measuring role of PM technique whose functioning features were presented in detail in [25] is, first of all, separation of medium responses into the effects from polarized and non-polarized light components. The latter one (that is present practically always) is not related to the anisotropic properties of the matter under investigation. It serves as a factor that masks valid signal and limits detectability of measuring systems. This may be avoided by using the property of polarized light to react to PM (contrary to non-polarized component). In that case, a photodetector converts the modulated component of light into variable signal that is separated from the constant component (generated by non-polarized light) using a selective amplifier. As a result, detectability of PM measuring systems (relative to variation of insulator anisotropy) increases by several orders of magnitude. Besides, we obtain an increase of the degree of accuracy of the measured result concerning its polarization (i.e., anisotropic) nature.
One of the analytical features of PM technique is its ability to expand light (in the general case, elliptically polarized) into circular and linear components. Another feature is that one of the linear components of polarized light that is determined by the Stokes parameter 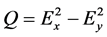 [28] (
[28] ( and
and 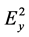 are the intensities of orthogonal components of light wave) has analytical properties. The meaning of component Q is that the mutual features of the functions in it, or those of any other effect under investigation (optical, photoelectric, magneto-optical etc.) vanish at subtraction. And the final result of subtraction that contains individual features of one of the terms and further amplification ensures, first of all, increased sensitivity of the system to variations of polarization state or physical reasons responsible for that. Besides, being an element (numerator) of the expression that determines mathematical derivative, the result of subtraction of the functions
are the intensities of orthogonal components of light wave) has analytical properties. The meaning of component Q is that the mutual features of the functions in it, or those of any other effect under investigation (optical, photoelectric, magneto-optical etc.) vanish at subtraction. And the final result of subtraction that contains individual features of one of the terms and further amplification ensures, first of all, increased sensitivity of the system to variations of polarization state or physical reasons responsible for that. Besides, being an element (numerator) of the expression that determines mathematical derivative, the result of subtraction of the functions  (under the condition
(under the condition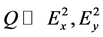 ) really is close in form to the derivative (with respect to the corresponding argument) but obtained by physical differentiation.
) really is close in form to the derivative (with respect to the corresponding argument) but obtained by physical differentiation.
Our measuring equipment involved a goniometer combined with a source of linearly polarized light. This system could measure angular polarization characteristics of internal reflection coefficients at different wavelengths l, or their spectral characteristics at specified angles of incidence q. The main object of measurement was characteristics of the polarization difference  of internal reflection coefficients for radiation electric fields whose azimuths periodically became perpendicular
of internal reflection coefficients for radiation electric fields whose azimuths periodically became perpendicular  and parallel
and parallel  to the plane of incidence.
to the plane of incidence.
It should be noted that the above parameter is a result of physical subtraction and, being the product of modulation procedure, has no errors accompanying that operation at mathematical procedure with results obtained by individual measurements. If necessary, we measured individual dependences for coefficients 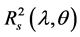 and
and 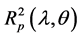 that were used at spectra analysis as auxiliary ones. The signals were registered with a lock-in nanovoltmeter. By setting reference signal phase, the parameter r(q) was made positive. This corresponded to the condition Rs(q) > Rp(q) that held for angles q < qcr below that of total internal reflection.
that were used at spectra analysis as auxiliary ones. The signals were registered with a lock-in nanovoltmeter. By setting reference signal phase, the parameter r(q) was made positive. This corresponded to the condition Rs(q) > Rp(q) that held for angles q < qcr below that of total internal reflection.
The engineering data of the measuring equipment were as follows. The wavelength of monochromatic polarized light was 632 nm. A grating monochromator with a halogen lamp and polarizer provided light with wavelength from the 400 - 1000 nm range (see Figure 1). The modulator was a dynamic phase plate [29] with modulation frequency of 50 kHz. The photodetector was a silicon photodiode.
The Аu-99.999% films were prepared by thermal evaporation of metal from a molybdenum heater in a vacuum (pressure of 10−3 Pa) onto the substrates of fused quartz that were at room temperature. The gold evaporation rate was about 1.5 nm/s; the film thickness (50 nm) was determined with a calibrated quartz resonator. The substrates (thickness of 1 mm) contacted, through an immersion liquid, the corresponding segment of the same material and made a semicylinder.
3. Results and Discussion
Figure 1 shows the results of measurement of the parameter r(l) (in the coordinates defined by the conditions of our experimental equipment) at fixed angles of incidence within the range involving the critical one. The angle values were chosen from the condition of the strongest dispersion of function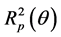 . That was the main attribute of the SPR effect and thus the reason for the observed evolution of the spectrum r(l). Indeed, the form of all the presented characteristics is typical for resonance effects at wavelengths 400 < l < 1000 nm. In addition, the characteristic feature of all the curves taken is their trend to merge at the ends of the above wavelength range. This indicates independence of the parameter r from the angle of incidence beyond that range. Since a fortiori there is no resonance interaction beyond the above wavelength range and parameter r(l) is always finite, it is doubtless true that the non-resonance component of reflection coefficients takes place within that range too.
. That was the main attribute of the SPR effect and thus the reason for the observed evolution of the spectrum r(l). Indeed, the form of all the presented characteristics is typical for resonance effects at wavelengths 400 < l < 1000 nm. In addition, the characteristic feature of all the curves taken is their trend to merge at the ends of the above wavelength range. This indicates independence of the parameter r from the angle of incidence beyond that range. Since a fortiori there is no resonance interaction beyond the above wavelength range and parameter r(l) is always finite, it is doubtless true that the non-resonance component of reflection coefficients takes place within that range too.
Of most importance is that all the characteristics contain to a variable degree indication of one more component (not improbable, of resonance type). This is indicated by a pronounced asymmetry of spectra profiles in Figure 2. Moreover, for a number of angular spectra this asymmetry acquires mirror position relative to the practically symmetric resonance curve (bold) for r(l)q=50˚.
It would seem that presentation of true dependences r(ω) by using the modern computer abilities (e.g., by approximating spectra with the Gauss functions) makes no problem. This could be so; however, presence in the functions r(l) of the component related to non-resonance reflection from metal and glass prevents obtaining them per se. Most probably, the spectrum of non-resonance component in Figure 1 would have to be a curve of finite amplitude of q = 40˚ type that joins angular characteristics merging differently beyond the range under investigation. Within that range, the amplitude of non-resonance component is determined by the experimental conditions: film thickness and optical constants (that depend on the film thickness and wavelength), as well as angle of incidence.
With allowance for the above considerations, it seems impossible to obtain that dependence for the corresponding angles (see Figure 2) using either methods of physics or mathematical formalism. At the same time, it is required because it serves as abscissa relative to which the approximation of experimental spectrum with the corresponding Gauss functions is to be reproduced. Therefore, in this work we attempted solving that problem
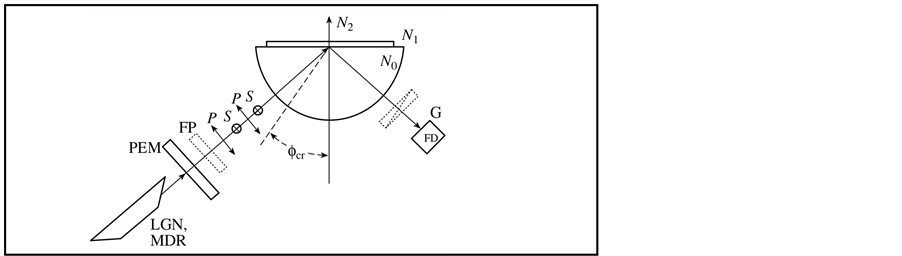
Figure 1. Optical scheme of the experimental setup for measuring the angular or spectral characteristics of the polarization difference ρ with application of polarization modulation: (LGN) He-Ne laser or (MDR) monochromator; (PP) quarter-wave phase plate; (PEM) photoelastic polarization modulator; (p, s) linear polarizations, whose azimuths are parallel and perpendicular to the plane of incidence; (G) Glan prism, (PD) photodetector; (φcr) critical angle of total internal reflection; and (N0, N1, N2) refractive indices of glass, metal, and air, respectively.
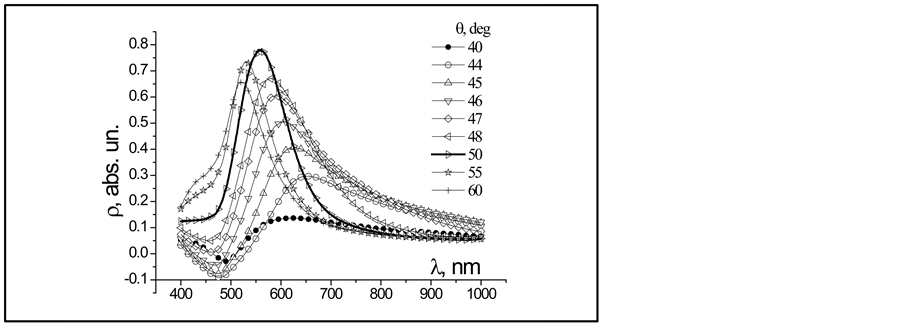
Figure 2. Evolution of the spectra r(l)q for Au film (thickness d = 50 nm) at variation of the angle of light incidence.
graphically. In doing so, we bore in mind that the degree of validity of the result will influence adequacy of such resonance parameters as frequency and damping time of SPR wave as well as reliability of its dispersion characteristic, as the final result of analysis.
To this end, let us use, first of all, the conceptual characteristic of the parameter r(q) for its analytical abilities mentioned before. Then computer simulation of the parameter r(q) should be made. The reason for doing so is that, as was shown by us in [25] for the case of a film with thickness d = 50 nm, the equation obtained using the Fresnel formulae for a three-layer glass—metal film—air system is in excellent agreement with the experimental data.
The preliminary results of the above procedure are presented in Figure 3(a) (at wavelength l = 630 nm and complex refractive index NAu = 0.2 + 3.6*i [30] ) for two limiting cases from the viewpoint of SPR appearing. One of them (full curve) corresponds to a film with thickness d = 120 nm (when resonance practically disappears). Another (dashed curve) corresponds to absence of film on the semicylinder surface (d = 0). For comparison the experimental curve for optimal (maximal SPR effect) film thickness d = 50 nm is also given (dash-dotted curve). One can see that non-resonance component in the dependence r(q)d=50 nm is similar to the dependence r(q)d=120 nm. The latter is almost purely non-resonance, except for a small departure from monotony at q = 45˚. The dependence r(q)d=50 nm is intermediate between the characteristics for the cases of a pure semicylinder and a thick metal film. One can see that the form of the curve corresponding to d = 50 nm contains the amplitude values characteristic of reflections at two film boundaries; their relation varies with film thickness.
The results of parameter r(q) simulation showed that, as film thickness goes down, or index of absorption of the film material decreases (due to reduction of wavelength of the light used), the distortion of monotonic dependence becomes stronger because of growth of resonance reflection at angles near qcr. In this case, one can obtain non-resonance component r(l) by artificial means. The procedure involves construction of a corresponding function whose amplitude values are to be obtained from the curve that fills a resonance gap in the angular dependences measured at the corresponding wavelengths. Such a curve may be the function r(q) of external reflection whose form is the closest to that of r(q)d=120 nm. When modeling it by an equation based on the Fresnel formulae, we used such optical parameters of the film at which the model curve (merging with the experimental dependence r(q) at qcr < q) would fill the resonance gap. A distinction in the amplitudes (resulting from difference between drops of refraction indices for external and internal reflections) was removed by an adjustable coefficient until coincidence with the experimental curve (corresponding to d = 50 nm).
The result obtained is shown in Figure 3(a) for wavelength l = 632 nm (dash-dotted curve). Its position is intermediate between those of the curves characterizing singly reflection from metal and glass. In the large, the dash-dotted curve contains the amplitudes of coefficients of reflection from metal and glass, in relations that depend generally on two film parameters, namely, thickness and index of absorption. An additional argument for curve validity is that it coincides with the real curve at the angles q < qcr and its extremum position at qcr < q lies in the coordinates r(q)max determined by the calculated dependence.
The same procedure is applied when constructing angular dependences r(q) for specified wavelengths from the range considered. To illustrate, Figure 3(b) shows dependence of parameter r(q) for another wavelength l =
 (a)
(a)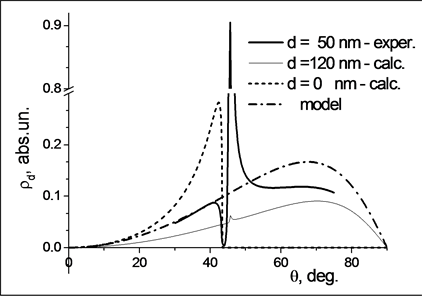 (b)
(b)
Figure 3. (a) Dependence r(q) at l = 632 nm for Au films of different thicknesses d and model non-resonance component for a film with d = 50 nm; (b) same as in (a) for a film with d = 50 nm; experimental and theoretical dependences r(q) as well as its non-resonance component (dashed curve) at l = 550 nm.
550 nm as compared with the calculated dependence (dashed curve) and approximating dependence (light curve) as model of non-resonance function. The number of such constructions was chosen from consideration of sufficiency of points necessary for passing through them of non-resonance spectra at fixed angles of incidence used in Figure 2. Then the corresponding ordinates of the same angles of the model curve were chosen, as coordinates of non-resonance spectra, from the angular dependences r(q) for different wavelengths (for the angles 40˚ £ q £ 60˚). Figure 4 presents only two of them (the limiting from the angle range considered).
The adequacy of the applied procedure is supported by the fact that the form of all non-resonance curves is similar to that of the experimental curve r(l)q=40˚ in Figure 2 (by definition, that curve contains no features of resonance reflection). As to the rest of non-resonance curves (not presented to avoid complication of figure), they lie (in logic sequence) in the space between the two presented curves. The nature of the dip (resembling resonance) in the curve r(l) at l @ 500 nm is formally related to non-monotony of dispersion of Au refractive index in that region. (The problem of physical reason for corresponding convergence of the curves for reflection coefficients  and
and  is beyond the framework of the present study and will be considered later).
is beyond the framework of the present study and will be considered later).
After performing subtraction of non-resonance dependences from the corresponding experimental curves in Figure 2, the procedure of approximating the result obtained by the Gauss functions becomes reasonable. To illustrate, Figure 5(a) presents the results of expansion of the spectrum corresponding to the angle of incidence q = 47˚. One can draw the following two conclusions. First, the practically ideal filling (the corresponding merging curves in Figure 5(b)) means good agreement between the experimental dependences and total approximating function and indicates credibility of the result obtained. Second, complete filling of the areas under the curves becomes possible with participation of three components only. For comparison, Figure 5(a) presents also expansion of spectrum at the angle of incidence q = 60˚. One can see that asymmetry of contours leads to inversion of component signs.
From the rest of normalized dependences r(l)q =40˚-60˚, the frequency and amplitude characteristics were built by expansion into the Gauss components. Before going to their interpretation, it seems appropriate to note that the three-layer structure used in the present work was considered earlier [31] in the framework of solving the Maxwell equations. The authors of [31] obtained the waveguide modes that appear at two metal-insulator interfaces adjoining the metal film. These modes are called symmetric (s-mode) and asymmetric (a-mode) because the electric field of the a-mode at the inner surface of metal film has inverse phase.
The authors of [31] believe (with some justice) that those solutions can be applied for description of distribution of fields appearing at interfaces on both film sides when exciting resonances at separate interfaces. This seems more probable when observing SPR in the Kretschmann-Raether [5] geometry used in the present work, when profile asymmetry of the field of excited surface polariton wave is superposed on phase asymmetry of the a-mode. At oblique incidence of light from a totally reflecting glass prism on a metal film, most of energy is concentrated near the metal-insulator interface with lower refractive index―quick mode (long-range). The small-energy (short-range) mode is concentrated near the metal-insulator interface with higher refractive index (i.e., at the inner surface of the film).
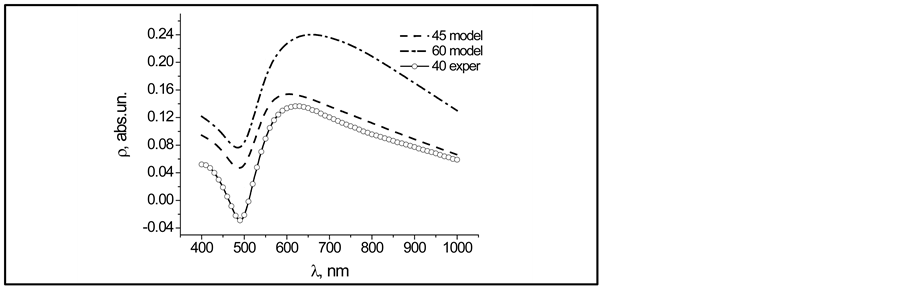
Figure 4. Spectral dependences of non-resonance component of the parameter r measured at the angle of incidence q = 40˚ and simulated for the angles q = 45˚ and 60˚.
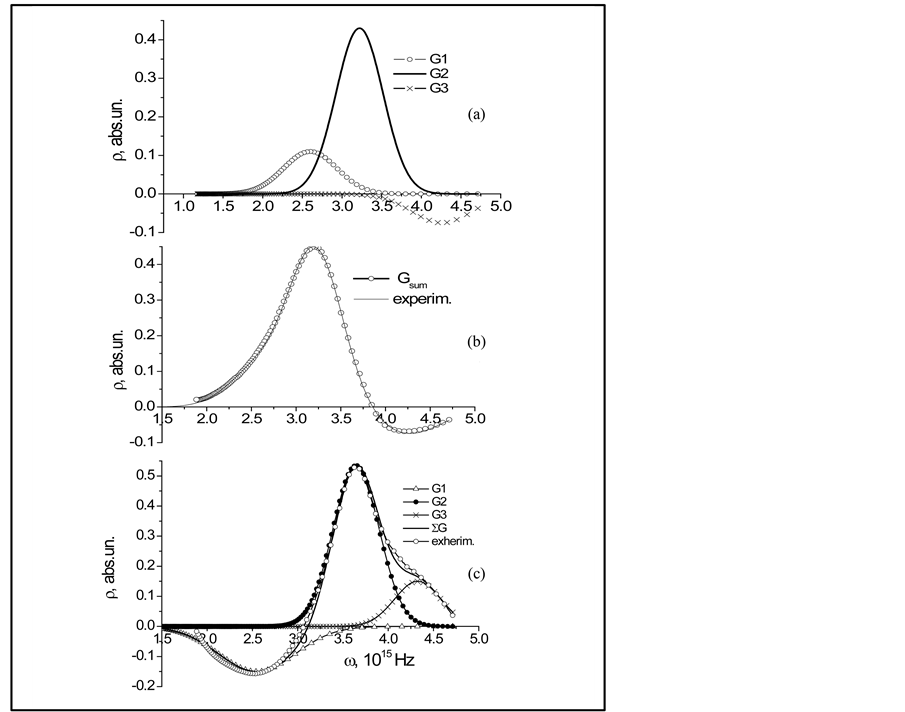
Figure 5. (a) Components of waveguide modes (s-short-range, long-range, ashort-range) in the experimental curve expansion into the Gauss functions; (b) approximation of the experimental dependence measured at q = 47˚ by the total Gauss function; (c) same as in (b) but at q = 60˚.
Just the latter wave mode (as a wave excited at the inner surface of the film) may change its phase. The reason for such a behavior of phase may be change of sign of electric polarization of the front surface at superposition on it of the fields of incident wave and that reflected from the back surface of the film. The real basis for such evolution is either spectrum-dependent variation of the index of absorption at a constant film thickness, or variation of film thickness at a fixed wavelength of light.
The results of spectral analysis shown in Figure 6 as dispersion characteristics ω(kSPR) serve as qualitative support of the above theoretical conclusions. These characteristics were obtained from the lines joining the points in the corresponding light lines 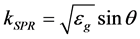 (εg is glass permittivity) that were built according to the above procedure. From Figure 6, it follows that the main waveguide mode (long-range SPP) or a surface plasmon-polariton wave is concentrated in the frequency range ω = (3 - 4) × 1015 Hz. The SPR component excited at the inner surface of gold film and called short-range waveguide mode [19] (short-range SPP) occupies two frequency ranges (above and below the main SPR frequencies).
(εg is glass permittivity) that were built according to the above procedure. From Figure 6, it follows that the main waveguide mode (long-range SPP) or a surface plasmon-polariton wave is concentrated in the frequency range ω = (3 - 4) × 1015 Hz. The SPR component excited at the inner surface of gold film and called short-range waveguide mode [19] (short-range SPP) occupies two frequency ranges (above and below the main SPR frequencies).
Figure 7 shows all the three components as amplitude dependence of the angle of incidence. This enables one to identify each of two versions of the short-range mode as either symmetric (whose sign is that of the main mode) or, correspondingly, antisymmetric. One can see more exact value (as compared to Figure 2) of the mirror symmetry angle q = 49˚. This fact can indicate the above-mentioned quality of expansion and validity of the result obtained, because the amplitude of the main mode becomes maximal at minimal values of two other modes.
4. Conclusions
Using the modulation polarimetry technique, it was shown that, even in such simple medium as a nanosized film of uniform metal, it is possible to detect different components of resonance interaction of electromagnetic radiation with electron-ion system of matter predicted in [14] . To this end, however, the development of a method for analysis of SPP spectral characteristic as parameter of polarization difference r(l) was needed. The necessity of this procedure was dictated by the revealed asymmetry of form of experimental characteristics of the parameter r(l). Moreover, this asymmetry undergoes mirror inversion of spectral characteristic relative to the angle of incidence q as well as sign of the parameter r(q).
Presence of non-resonance spectral components whose values remained unknown prevented the expansion of spectra into components. We developed a special procedure for determination of non-resonance component in
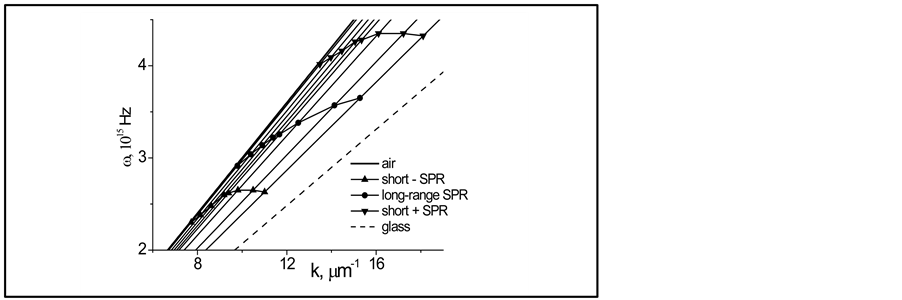
Figure 6. SPP dispersion characteristics ω(k) in Au film with d = 50 nm.

Figure 7. The Gauss function components approximating normalized rSPR as function of the angle of light incidence.
the parameter r(l) based on simulation of angular characteristics of the polarization difference wavelength . As a result, we obtained monotonic dependences r(q)mod that filled a resonance gap in similar function of the real specimen, thus making it possible to determine non-resonance amplitudes for the corresponding wavelength. Then the spectra of non-resonance components were built for the corresponding angles from the set of amplitudes r(q)mod at certain wavelengths from the range used. The normalized spectral dependence of the resonance parameter r(l)SPP was obtained by subtraction of each non-resonance component from the corresponding spectrum r(l)q.
. As a result, we obtained monotonic dependences r(q)mod that filled a resonance gap in similar function of the real specimen, thus making it possible to determine non-resonance amplitudes for the corresponding wavelength. Then the spectra of non-resonance components were built for the corresponding angles from the set of amplitudes r(q)mod at certain wavelengths from the range used. The normalized spectral dependence of the resonance parameter r(l)SPP was obtained by subtraction of each non-resonance component from the corresponding spectrum r(l)q.
The practically ideal agreement between the obtained approximating total Gauss function and experimental curve r(l)SPP indicates validity of the procedure used by us and reliability of the dispersion characteristics. Besides, the method of expansion of the normalized spectral dependence r(l)SPR into components enabled us to detect the long-range and short-range waveguide modes described in [32] and identify them as polariton waves at the outer and inner surface of metal film, respectively. A transition from symmetric to antisymmetric state was found in the spectral and angular characteristics of the short-wavelength mode at a fixed angle of light incidence. It should be noted that both (symmetric and antisymmetric) modes of short-range SPP practically vanish at that angle (q = 49˚), at least in the specimen of 50 nm thickness.
References
- Otto, A. (1968) Zeitschrift fur Physik, 216, 398-410.
- Agranovich, V.M. and Mills, D.L. (1982) Surface Polaritons: Electromagnetic Waves at Surfaces and Interfaces, North Holland. Elsevier, North Holland
- Raether, H. (1988) Surface Plasmons on Smooth and Rough Surfaces and on Gratings. Springer, Heidelberg.
- Maier, S.A. (2007) Plasmonics: Fundamentals and Applications, Springer, Berlin. http://dx.doi.org/10.1007/0-387-37825-1_2
- Kretschmann, E. and Raether, H. (1968) Zeitschrift Fur Naturforschung Part A—Astrophysik Physik Und Physikalische Chemie A, 23, 2135-2136.
- Otto, A. (1969) Zeitschrift fur Physik, 219, 227-233.
- Berini, P. (2009) Advances in Optics and Photonics, 1, 484-588. http://dx.doi.org/10.1364/AOP.1.00041943-8206/09/030484-105
- Fukui, M., So, V.C.Y. and Normandin, R. (1979) Physica Status Solidi (b), 91, K61-K64. http://dx.doi.org/10.1002/pssb.2220910159
- Economou, E.N. (1969) Physical Review, 182, 539-554. http://dx.doi.org/10.1103/PhysRev.182.539
- Quail, J.C., Rako, J.G. and Simon, H.J. (1983) Optics Letters, 8, 377-379. http://dx.doi.org/10.1364/OL.8.000377
- Zayats, A.V., Smolyaninov, I.I. and Maradudin, A.A. (2005) Physics Reports, 408, 131-314. http://dx.doi.org/10.1016/j.physrep.2004.11.001
- Gramotnev, D.K. and Vernon, K.C. (2007) Applied Physics B: Lasers and Optics, 86, 7-17. http://dx.doi.org/10.1063/1.2732699
- Kovacs, G.J. (1978) Journal of the Optical Society of America, 68, 1325-1332. http://dx.doi.org/10.1364/JOSA.68.001325
- Burke, J.J., Stegeman, G.I. and Tamir, T. (1986) Physical Review B, 33, 5186-5201. http://dx.doi.org/10.1103/PhysRevB.33.5186
- Craig, A.E., Olson, G.A. and Sarid, D. (1983) Optics Letters, 8, 380-382. http://dx.doi.org/10.1364/OL.8.000380
- Tien, P.K. and Ulrich, R. (1970) Journal of the Optical Society of America, 60, 1325-1337. http://dx.doi.org/10.1364/JOSA.60.001325
- Agranovich, V.M., Mal’shukov, A.G. and Mekhtiev, M.A. (1973) Soviet Physics JETP, 36, 1203-1209.
- Ignatyeva, D.O., Kalish, A.N., Levkina, G.Y. and Sukhorukov, A.P. (2012) Physical Review A, 85, 043804-043809. http://dx.doi.org/10.1103/PhysRevA.85.043804
- Craig, A.E., Olson, G.A. and Sarid, D. (1983) Optics Letters, 8, 380-382. http://dx.doi.org/10.1364/OL.8.000380
- Sarid, D. (1981) Physical Review Letters, 47, 1927-1930. http://dx.doi.org/10.1103/PhysRevLett.47.1927
- Sarid, D., Deck, R.T., Craig, A.E., Hickernell, R.K., Jameson, R.S. and Fasano, J.J. (1982) Applied Optics, 21, 3993- 3995. http://dx.doi.org/10.1364/AO.21.003993
- Woolf, D., Loncar, M. and Capasso, F. (2009) Optics Express, 17, 19996-20011. http://dx.doi.org/10.1364/OE.17.019996
- Yoon, H., Maier, S.A., Bradley, S.D. and Stavrinou, P. (2011) Optical Materials Express, 1, 1127-1138. http://dx.doi.org/10.1364/OME.1.001127
- Singh, S. and Gupta, B.D. (2010) Measurement Science and Technology, 21, 115202-115210. http://dx.doi.org/10.1088/0957-0233/21/11/115202
- Berezhinsky, L.J., Maksimenko, L.S., Matyash, I.E., Rudenko, S.P. and Serdega, B.K. (2008) Optics and Spectroscopy, 105, 281-289. http://dx.doi.org/10.1134/S0030400X08080146
- Serdega, B.K., Rudenko, S.P., Maksimenko, L.S. and Matyash, I.E. (2011) Plasmonic Optical Properties and the Polarization Modulation Technique. In: Mishchenko, M.I., Yatskiv, Y.S., Rosenbush, V.K., Videen, G., Eds., Polarimetric Detection, Characterization and Remote Sensing NATO Science for Peace and Security Series C: Environmental Security, Springer, Berlin, 473-500. http://dx.doi.org/10.1007/978-94-007-1636-0_18
- Grinevich, V.S., Filevska, L.M., Matyash, I.E., Maximenko, L.S., Mischuk, O.N., Rudenko, S.P., Serdega, B.K., Smyntyna, V.A. and Ulug, B. (2012) Thin Solid Films, 522, 452-456. http://dx.doi.org/10.1016/j.tsf.2012.08.054
- Gerrard, A. and Burch, J.M. (1975) Introduction to Matrix Methods in Optics. Wiley, London.
- Jasperson, S.N. and Schnatterly, S.E. (1969) Review of Scientific Instruments, 40, 761-767. http://dx.doi.org/10.1063/1.1684062
- Palik, E.D. (1991) Handbook of Optical Constants of Solids. Academic Press, New York.
- Nikolajsen, T., Leosson, K., Salakhutdinov, I. and Bozhevolnyi, S.I. (2003) Applied Physics Letters, 82, 668-670. http://dx.doi.org/10.1063/1.1542944
NOTES

1Here we mean the value of reflection coefficient 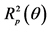 of p-polarized light measured (in ordinate of the angular dependence) from the extremum near the critical angle (cr to the current value.
of p-polarized light measured (in ordinate of the angular dependence) from the extremum near the critical angle (cr to the current value.

