Journal of Modern Physics
Vol.06 No.02(2015), Article ID:54190,4 pages
10.4236/jmp.2015.62017
A Supplement to the Invariance Principle of the Speed of Light and the Quantum Theory
Yuanjie Li1*, Wenchuan Jia2, Jiale Wang3
1Huazhong University of Science and Technology, Wuhan, China
2School of Mechanical Engineering and Automation, Shanghai University, Shanghai, China
3South University of Science and Technology of China, Shenzhen, China
Email: *yuanjie_li@sina.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 27 January 2015; accepted 13 February 2015; published 25 February 2015
ABSTRACT
Richard Feynman once said, “I think it is safe to say that no one understands Quantum Mechanics”. The well-known article on the Einstein-Podolsky-Rosen (EPR) paradox brought forth further doubts on the interpretation of quantum theory. Einstein’s doubt on quantum theory is a double- edged sword: experimental verification of quantum theory would contradict the hypothesis that speed of light is finite. It has been almost a century since the creation of quantum theory and special relativity, and the relevant doubts brought forward remain unresolved. We posit that the existence of discontinuity points and quantum wormholes would imply superluminal phenomenon or infinite speed of light, which provides for an important supplement to the invariance principle of the speed of light and superluminal phenomena. This can potentially resolve the inconsistency between special relativity and quantum theory.
Keywords:
Invariance Principle of the Speed of Light, Superluminal Phenomena, Uncertainty Principle, Quantum Nonlocality, Quantum Wormholes

1. Introduction
Since quantum mechanics was created, the explanation of wave function has always been an issue puzzling scientists. Bohn’s theory of probability amplitude gave us an explanation on what the wave of probability amplitude really is. Is it the result of multiple acts of a single particle, one-time behavior of numerous particles, or one-time behavior of a single particle? It is a problem that scholars have argued for a long time [1] -[3] . As technology advanced, new experiments revealed a great number of quantum nonlocality and superluminal phenomena [4] , which made it even harder for theorists to explain. From the old experiments such as wave-particle duality, Schrödinger cat, EPR paradox, to the more recent ones like interference of single photon, quantum corral and quantum information communication, all of these pose great challenges to quantum mechanics [5] - [9] . Recently, two Australian mathematicians James M. Hill and Barry J. Cox provided the mathematical form of special relativity under the superluminal phenomena [10] . However, in this article, we will discuss it physically.
2. Hundred Years’ Entanglement of Quantum and Special Relativity
Let’s first look at an example of an atom, the scale of the electron  m, the scale of the atom la < 10−11 - 10−10 m, and so the scale ratio
m, the scale of the atom la < 10−11 - 10−10 m, and so the scale ratio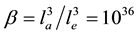 . When using the STM to scan the whole atom (Figure 1), the electrons inside the atom need to traverse the whole atom in
. When using the STM to scan the whole atom (Figure 1), the electrons inside the atom need to traverse the whole atom in 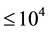 s, (the scanning time of the STM). So the speed probably is:
s, (the scanning time of the STM). So the speed probably is:  m/s, which is much greater than the speed of the light. We see that existence of wave function will lead to the result of super luminance.
m/s, which is much greater than the speed of the light. We see that existence of wave function will lead to the result of super luminance.
EPR paradox is a discussion about entanglement state, and it can be symbolically expressed as
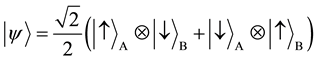
The entanglement state arises in TQW, and switches between  and
and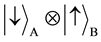 . As shown in Figure 2, the information on particle A’s spin magnetic dipole moment is transmitted to particle B through superluminal magnetic photons. Such information, which would subsequently determine particle B’s spin magnetic dipole moment, is formed inside TQW. It would travel through countless wormholes afterwards. It is to be noticed that even when outside a wormhole, probability amplitude still exhibits similar patterns. In short, superluminal motion inside TQW allows us to explain quantum nonlocality without violating the special theory of relativity established in continuous time-space. We believe that the continuous time-space is filled with numerous wormholes, which are not detectable with existing experimental apparatus. Micro particles’ entrance into these wormholes would inevitably result in superluminal phenomena and quantum nonlocality. Such event is compatible with Einstein’s special theory of relativity.
. As shown in Figure 2, the information on particle A’s spin magnetic dipole moment is transmitted to particle B through superluminal magnetic photons. Such information, which would subsequently determine particle B’s spin magnetic dipole moment, is formed inside TQW. It would travel through countless wormholes afterwards. It is to be noticed that even when outside a wormhole, probability amplitude still exhibits similar patterns. In short, superluminal motion inside TQW allows us to explain quantum nonlocality without violating the special theory of relativity established in continuous time-space. We believe that the continuous time-space is filled with numerous wormholes, which are not detectable with existing experimental apparatus. Micro particles’ entrance into these wormholes would inevitably result in superluminal phenomena and quantum nonlocality. Such event is compatible with Einstein’s special theory of relativity.
Obviously, each electron must have covered the whole area of the corral at least once within this short time interval. If the process is achieved through space passage, nodes of the standing wave must have been passed through multiple times. Thus, the probability at nodes cannot be zero, which contradicts the experimental results that possibility at the nodes is exactly zero! Therefore, it seems that the motion of electrons in the fence also transcends time and space through some “underground tunnel”. Given the analysis above, we conclude that the
Figure 1. Electron cloud of an atom.
Figure 2. Entanglement state.
motion of those microscopic particles cannot be achieved through space passage, for otherwise superluminal phenomena exist and spatial probability density cannot be zero. In other words, the existence of probability function will lead to the result of super luminance.
Mathematically, just like the Newton’s equation of gravity is an action of super distance, the probability density function is completely expressed in the whole space. Physically, it means that the micro-particles are everywhere at the same time. The only difference is that its appearance at different places has different probability. Such phenomenon can occur only if the speed of the micro-particles’ random motion is infinitely large. However, this result once again disobeys Einstein’s special relativity.
3. Break Point of Time and TQW
Suppose Stephen Hawking’s hypothesis holds [5] - [7] , and the break points of space and time are of Planck length’s scale 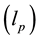 and Planck time’s scale
and Planck time’s scale  respectively, then they each forms SQW and TQW through time and space. Thus if TQW (the break point of time) is also a way for particle to go from A to B (Figure 3), then we can provide a satisfactory explanation to the two questions above. Furthermore, based on the string theory, the wormhole in compact dimension space (EQW) may exist as well.
respectively, then they each forms SQW and TQW through time and space. Thus if TQW (the break point of time) is also a way for particle to go from A to B (Figure 3), then we can provide a satisfactory explanation to the two questions above. Furthermore, based on the string theory, the wormhole in compact dimension space (EQW) may exist as well.
Suppose for now the hypothesis that a micro particle in TQW can excite superluminal and super high frequency wave of probability density (Figure 4), which recovers and becomes under the control of special relativity upon exit from TQW. Note that special relativity can be measured in space-time. The above hypothesis can be established with the uncertainty principle.
1) Quantum wave of probability amplitude is a wave with changing frequencies, which has super high frequency inside the TQW. This result can be deduced from uncertainty principle. Given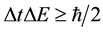 , as
, as 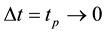 ,
, 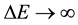 or
or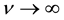 . This implies that the speed of the quantum wave of probability amplitude
. This implies that the speed of the quantum wave of probability amplitude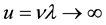 , i.e. the speed of wave is beyond the speed of light. Outside the TQW it becomes under the control of Einstein’s special relativity because the order of the measured data is much higher than the Planck order. As a result, superluminal phenomena only happen inside the TQW.
, i.e. the speed of wave is beyond the speed of light. Outside the TQW it becomes under the control of Einstein’s special relativity because the order of the measured data is much higher than the Planck order. As a result, superluminal phenomena only happen inside the TQW.
2) It is worth emphasizing that although the “entrance” of the TQW 
Now, let’s bring our attention to the formation of quantum corral. Theoretically, it holds that the probability amplitude is a one-time behavior of a single electron taking place in TQW (Figure 5).
Figure 3. Movement in TQW.
Figure 4. Quantum corral (data from interenet).
Figure 5. One-time formatted wave of quantum corral in TQW.
As for SQW, notice that as


4. A Supplement to the Invariance Principle of the Speed of Light
Our supplement to the invariance principle of the speed of light is as follows: the speed of light is constant within any inertial system, and is finite within measurable space-time. However, speed of light is infinite at points of discontinuity in space-time as well as inside the TQW. Therefore the speed of static particle with non- zero mass at points of discontinuity in time-space as well as points inside the TQW can also be infinite, albeit still smaller than the speed of light. In general, superluminal speed refers to speed that is greater than the conventional speed of light
Based on this supplement to the invariance principle of the speed of light, we can then give a reasonable explanation to the quantum nonlocality phenomena found experimentally.
5. Superluminal in TQW and Special Relativity
An important conclusion from Einstein’s special relativity is Lorentzin variance in all inertial systems. Here we examine the two 4-dimensional invariants: space-time line element and energy-dynamic tensor.
Space-time line element as given by 

In TQW,


Energy-dynamic tensor forms a 4-dimensional invariant






As can be seen, given Lorentz invariance, superluminal phenomenon in TQW is in fact a result of the special theory of relativity. The speed of light remains constant in continuous space-time, and only goes to infinity inside the wormholes at points of discontinuity. The inconsistency between special relativity and superluminal phenomena can now be bridged with the above amendment to the invariance principle of special relativity.
6. Conclusion
A film can be thought of as a series of static images played rapidly in succession, creating the illusion that the
Figure 6. Nature is like a movie player.
motion is actually occurring. Even though micro-particles are invisible inside TQW, their intermittent appearances outside the TQW over a short time interval resemble a series of “images” played rapidly in succession. This creates the “film” that is observable to human eyes. In this sense, the Mother Nature has always been a natural movie player, as shown in Figure 6.
Acknowledgements
Research supported by the National Natural Science Foundation of China under grant 51121002.
References
- Einstein, A., Podolsky, B. and Rosen, N. (1935) Physical Review, 47, 777-780. http://dx.doi.org/10.1103/PhysRev.47.777
- Bell, J.S. (1966) Reviews of Modern Physics, 38, 447-452. http://dx.doi.org/10.1103/RevModPhys.38.447
- Henderson, G.A. (1981) Physical Review A, 23, 19-20.
- Kwiat, P.G., Barraza-Lopez, S., Stefanov, A. and Gisin, N. (2000) Nature, 409, 1014-1017. http://dx.doi.org/10.1038/35059017
- Yamamoto, H. (1984) Physical Review D, 30, 1727-1732.
- Snyder, H.S. (1947) Physical Review, 71, 38-41. http://dx.doi.org/10.1103/PhysRev.71.38
- Chaichian, M., Demichev, A., Prešnajder, P. and Tureanu, A. (2001) The European Physical Journal C, 20, 767-772. http://dx.doi.org/10.1007/s100520100664
- Bailin, D. and Love, A. (1987) Reports on Progress in Physics, 50, 1087-1170. http://dx.doi.org/10.1088/0034-4885/50/9/001
- Polchinski, J. (1998) String Theory. UK Cambridge University Press, Cambridge.
- Hill, J.M. and Cox, B.J. (2012) Proceedings of the Royal Society A, 471. http://dx.doi.org/10.1098/rspa.2012.0340
NOTES
*Corresponding author.








