Journal of Modern Physics
Vol.4 No.12(2013), Article ID:40914,6 pages DOI:10.4236/jmp.2013.412196
The Triggering Role of Carrier Mobility in the Fractional Quantum Hall Effect Formation—An Evidence in Graphene
Institute of Physics, Wrocław University of Technology, Wrocław, Poland
Email: janusz.jacak@pwr.wroc.pl
Copyright © 2013 Janusz Jacak, Lucjan Jacak. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received September 20, 2013; revised October 25, 2013; accepted November 21, 2013
Keywords: Graphene; FQHE; Braid Groups; Composite Fermions
ABSTRACT
Recent experiments with suspended graphene have indicated the crucial role of carrier mobility in the competition between Laughlin collective state and insulating state, probably of Wigner-crystal-type. Moreover, the fractional quantum Hall effect (FQHE) in graphene has been observed at a low carrier density where the interaction is reduced as a result of particles dilution. This suggests that the interaction may not be a sole factor in the triggering of FQHE as it was expected to be based on the standard formulation of the composite fermion model. Here, the topological arguments are presented to explain the observed features of the FQHE in graphene and the triggering role of carrier mobility in formation of the Laughlin state.
1. Introduction
While the integer quantum Hall effect (IQHE) is regarded as a single-particle effect and by topology conditioned phenomenon related to Landau level (LL) quantization (as it has been especially convincingly argued in the topological quantum pump model of Laughlin [1]) with vital role played by impurity states [2], the FQHE is essentially a collective state arrangement with primary role of the interaction. This is noticeable due to form of Laughlin wave function [3] which turns out [4,5] to be an exact ground state for 2D system of charged particles at the presence of magnetic field at lowest LL filling 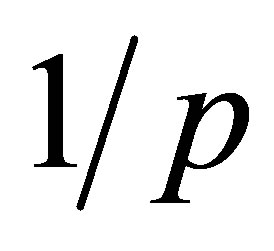 (
(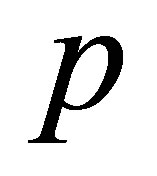 —odd) when the short range part of Coulomb interaction is taken into account only (expressed by so-called Haldane pseudopotentials, i.e., matrix elements of Coulomb interaction in the base of relative angular momentum
—odd) when the short range part of Coulomb interaction is taken into account only (expressed by so-called Haldane pseudopotentials, i.e., matrix elements of Coulomb interaction in the base of relative angular momentum 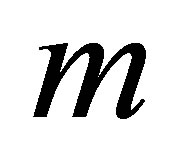 of electron pair; the short range part of the interaction is limited by the
of electron pair; the short range part of the interaction is limited by the 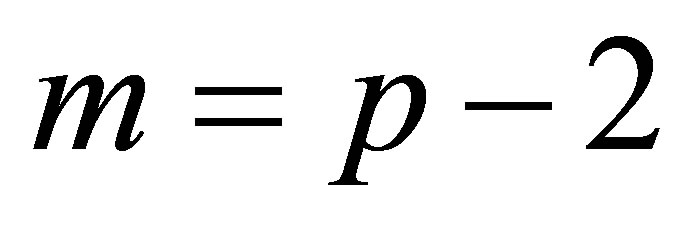 Haldane term for the
Haldane term for the 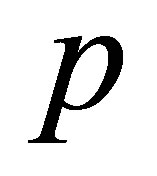 -th FQHE state and the long range tail with
-th FQHE state and the long range tail with 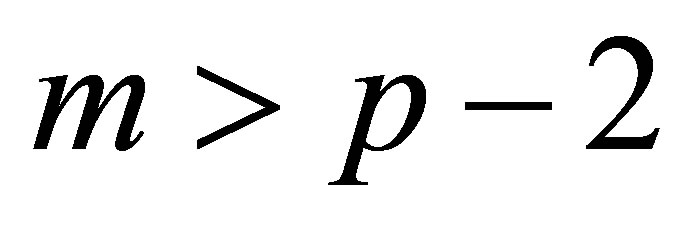 does not influence significantly this state [5]). Despite the strong correlation effects, the essential physics of the FQHE was successfully grasped within an effectively single particle model of composite fermions (CFs) [6], of only residually interacting particles associated with auxiliary field flux tubes each (
does not influence significantly this state [5]). Despite the strong correlation effects, the essential physics of the FQHE was successfully grasped within an effectively single particle model of composite fermions (CFs) [6], of only residually interacting particles associated with auxiliary field flux tubes each (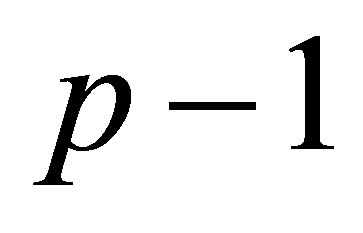 flux quanta of the auxiliary field is assumed to be fixed in some way to each particle). These composite particles gain the statistics required by the Laughlin function as a result of the Aharonov-Bohm effect, when particles interchange together with the flux tubes fixed to them. The CF concept is commonly accepted because of its appealing single particle picture and further modeling by variants of Chern-Simons field suitable to efficient calculations, supported with a good agreement with exact diagonalizations, especially inside the lowest LL (LLL) [7,8].
flux quanta of the auxiliary field is assumed to be fixed in some way to each particle). These composite particles gain the statistics required by the Laughlin function as a result of the Aharonov-Bohm effect, when particles interchange together with the flux tubes fixed to them. The CF concept is commonly accepted because of its appealing single particle picture and further modeling by variants of Chern-Simons field suitable to efficient calculations, supported with a good agreement with exact diagonalizations, especially inside the lowest LL (LLL) [7,8].
Recent experimental investigations of the FQHE in graphene [9,10] have shed, however, new light on this correlated state and it seems to go beyond explanation ability of CF treatment that concentrates solely on the interaction. If one imagines CFs to be an analog to solidstate Landau quasiparticles dressed with the interaction, i.e., presuming that the local flux tubes are a result of the interaction [7,8], one would lose important topological features and encounter problems with new observations in suspended graphene samples indicating that the carrier mobility (besides the interaction) plays a triggering role for FQHE organization.
In the present paper, we revisit the foundations of the composite fermion model and supply a topological argumentation for the FQHE that is in agreement with recent observations in suspended graphene, thereby highlighting the important role of carrier mobility besides the interaction in FQHE.
2. IQHE and FQHE in Graphene —Description of Experimental Results
A single-atom-thick layer of graphite (an allotropic form of carbon) known as graphene creates a hexagonal 2D structure, with a Bravais lattice of two vectors:
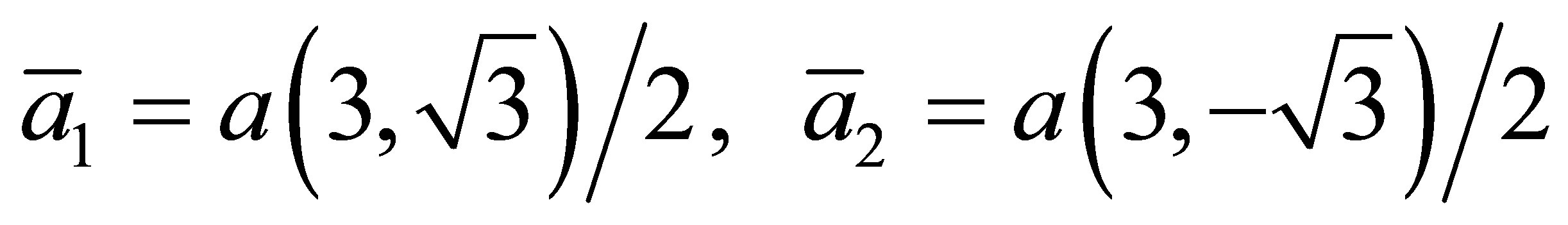 (
(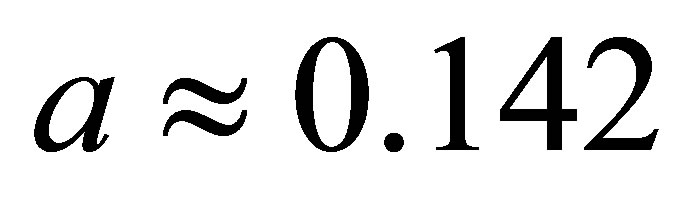 nm, distance between carbon atoms) with two carbon atoms per unit cell, Figure 1(a)). This results in the creation of a double triangular lattice—a hexagonal structure of carbon atoms arranged in a honeycomb pattern, an outspread nanotube. Hybridized carbon atom bonds
nm, distance between carbon atoms) with two carbon atoms per unit cell, Figure 1(a)). This results in the creation of a double triangular lattice—a hexagonal structure of carbon atoms arranged in a honeycomb pattern, an outspread nanotube. Hybridized carbon atom bonds  of the
of the  type lead to the two-dimensional structure, whereas
type lead to the two-dimensional structure, whereas 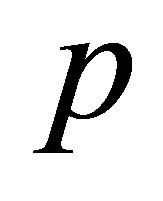 orbitals perpendicular to the plane hybridize to type
orbitals perpendicular to the plane hybridize to type  of the band structure (well described in the approximation of a strong coupling with the inclusion of nearest neighbors and subsequent neighbors) with hole valley (valence band) and electron valley (conduction band) met in points
of the band structure (well described in the approximation of a strong coupling with the inclusion of nearest neighbors and subsequent neighbors) with hole valley (valence band) and electron valley (conduction band) met in points  and
and 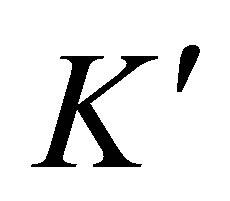 at the border of a hexagonal Brillouin zone [11,12], Figure 1(b)).
at the border of a hexagonal Brillouin zone [11,12], Figure 1(b)).
Both bands meet in these points (non-gap semiconductor) and have a conical shape (near points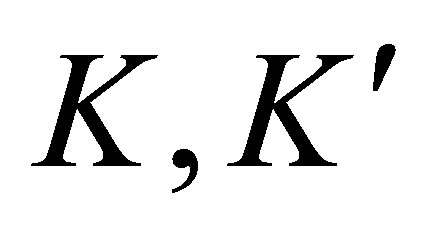 , neglecting next-neighbors hopping), which means that the relation between energy and momentum (the distance
, neglecting next-neighbors hopping), which means that the relation between energy and momentum (the distance
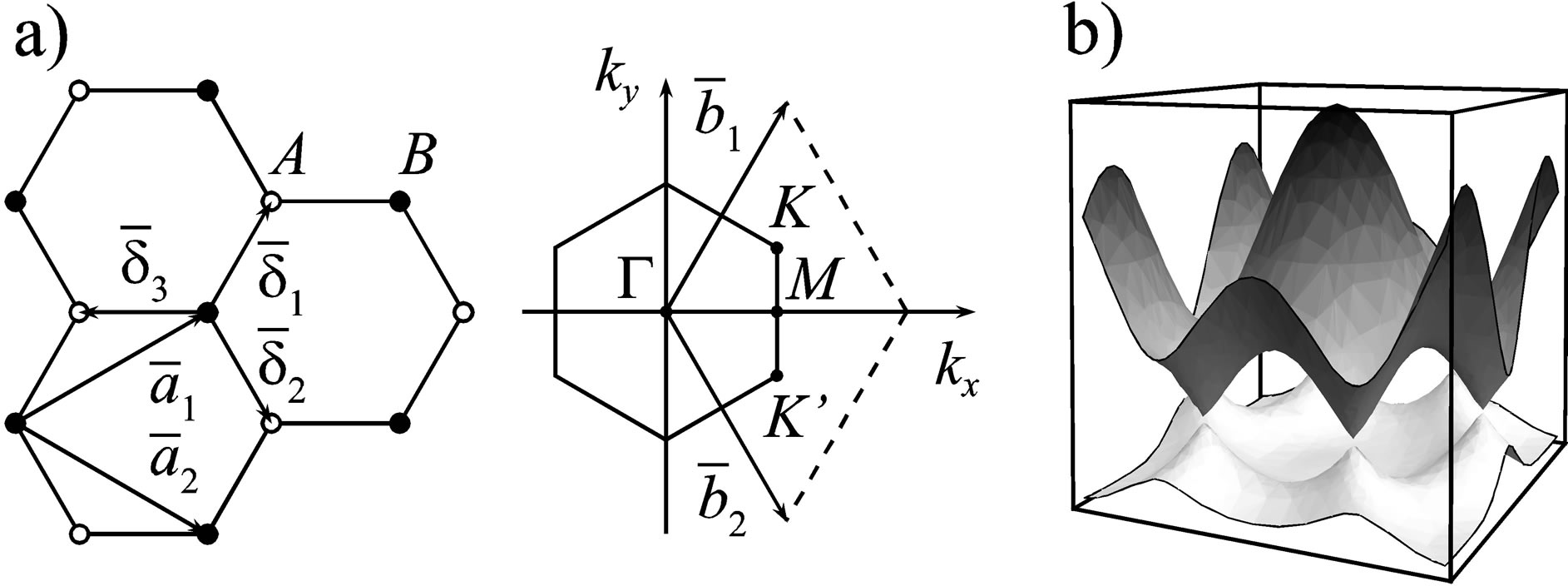
Figure 1. (a) A two-sublattices 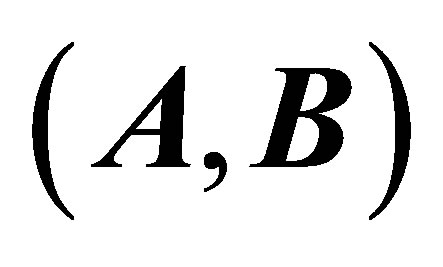 triangular structure of graphene,
triangular structure of graphene, 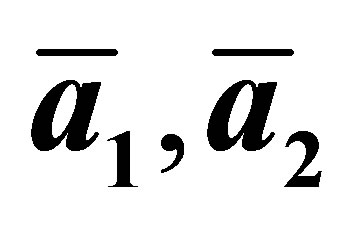 are Bravais lattice vectors,
are Bravais lattice vectors, 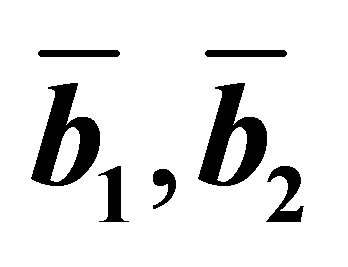 are vectors of reciprocal lattice; (b) The band structure of graphene, band type
are vectors of reciprocal lattice; (b) The band structure of graphene, band type , in a model of strong coupling, in compliance with the relation,
, in a model of strong coupling, in compliance with the relation, 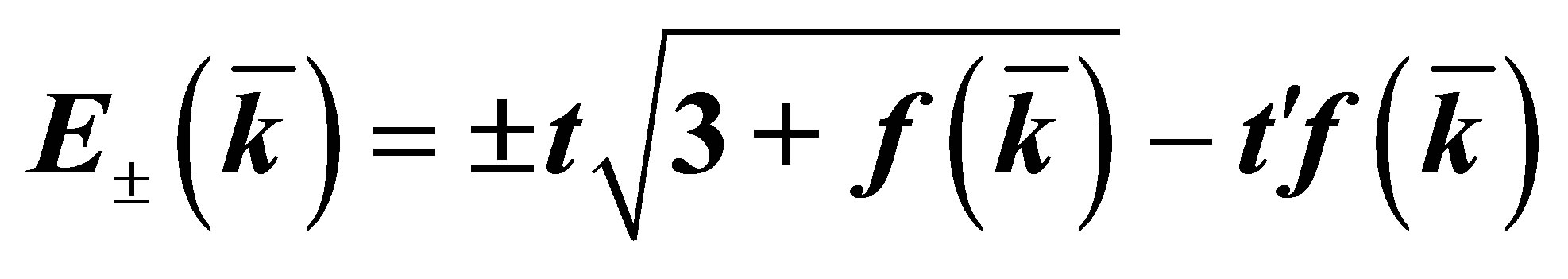 , where
, where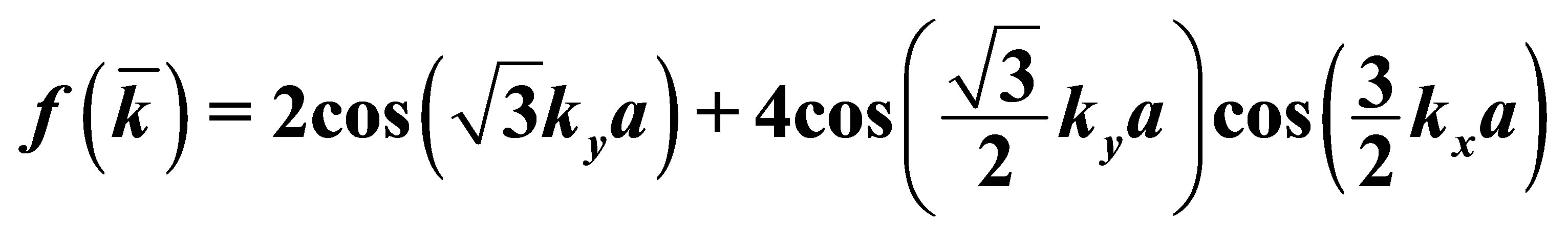 ,
, 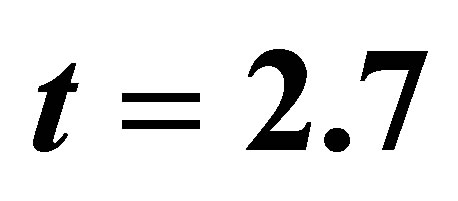 eV—hopping energy to the nearest neighbors (between sublattices, vectors
eV—hopping energy to the nearest neighbors (between sublattices, vectors ),
),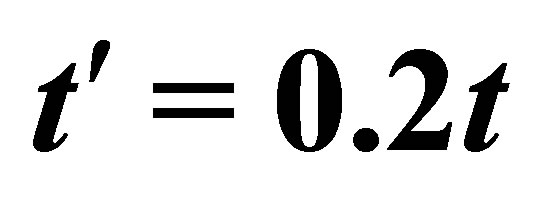 —hopping energy to next-nearest neighbors (inside the sublattices),
—hopping energy to next-nearest neighbors (inside the sublattices), 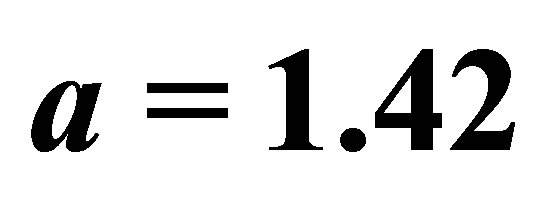 Å, the ideal Dirac points
Å, the ideal Dirac points  and
and  for
for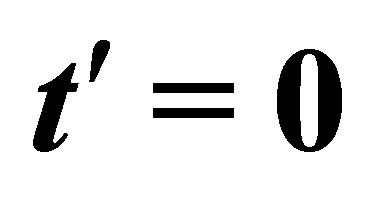 .
.
from points of contact in momentum space) is linear with respect to momentum length. The appropriate band Hamiltionian (within the strong coupling approximation including the nearest neighbors and accounting for both sublattices numerated with a pseudospin) is formally equivalent to the description of relativistic fermions with zero rest mass (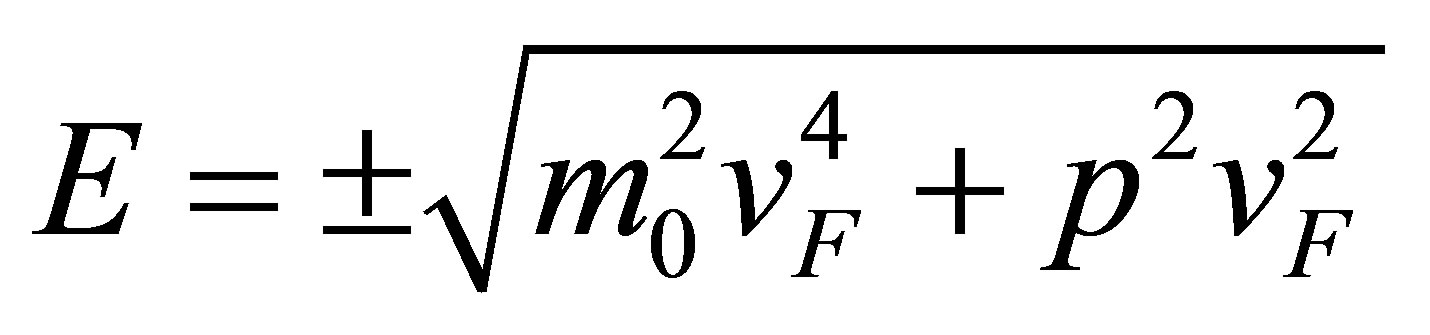 , with
, with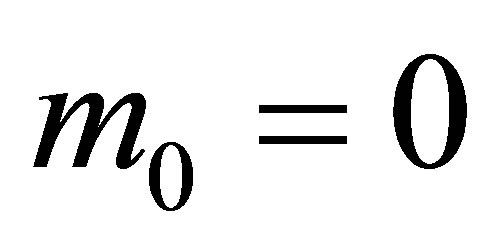 ), i.e.of the Dirac equation with the velocity of light replaced by the Fermi velocity,
), i.e.of the Dirac equation with the velocity of light replaced by the Fermi velocity, 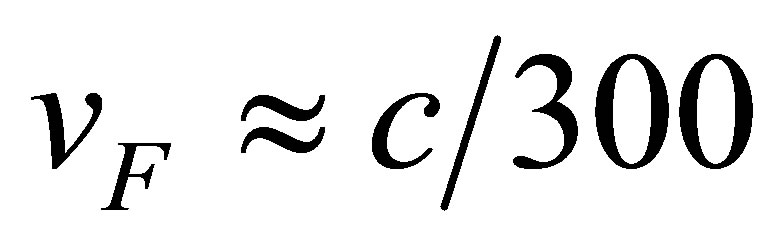 [12,13]. Therefore, the dynamics equation looks as follows,
[12,13]. Therefore, the dynamics equation looks as follows,
 where the Pauli matrix vector corresponds to the pseudospin structure related to two sublattices [12,14] (wave functions are spinors). The zero mass of the Dirac fermions leads to numerous consequences and electron anomalies in the properties of graphene [12,14-16]. For Dirac particles with zero rest mass, momentum uncertainty also leads to energy uncertainty (contrary to nonrelativistic case, where the relation between uncertainty of position and momentum are independent from the relation of uncertainty of energy and time), which leads to the time evolution mixing together particle states with hole (anti-particle) states for relativistic type dynamics. For zero-mass Dirac electrons the scaling of cyclotron energy is different as well (
where the Pauli matrix vector corresponds to the pseudospin structure related to two sublattices [12,14] (wave functions are spinors). The zero mass of the Dirac fermions leads to numerous consequences and electron anomalies in the properties of graphene [12,14-16]. For Dirac particles with zero rest mass, momentum uncertainty also leads to energy uncertainty (contrary to nonrelativistic case, where the relation between uncertainty of position and momentum are independent from the relation of uncertainty of energy and time), which leads to the time evolution mixing together particle states with hole (anti-particle) states for relativistic type dynamics. For zero-mass Dirac electrons the scaling of cyclotron energy is different as well (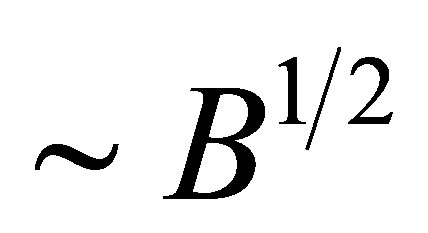 , and not
, and not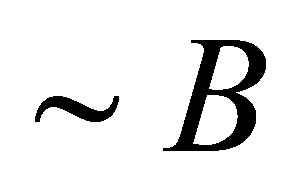 , as in the case of non-relativistic particles). The value of this energy is also different, and larger by far (two orders of magnitude larger than the corresponding one in classical materials, i.e., it is [due to zero mass in Dirac point] as much as about 1000 K, for 10 T field), which allows to observe the IQHE in graphene even at room temperatures [15,16]. There is, however, an anomalous IQHE observed here (for
, as in the case of non-relativistic particles). The value of this energy is also different, and larger by far (two orders of magnitude larger than the corresponding one in classical materials, i.e., it is [due to zero mass in Dirac point] as much as about 1000 K, for 10 T field), which allows to observe the IQHE in graphene even at room temperatures [15,16]. There is, however, an anomalous IQHE observed here (for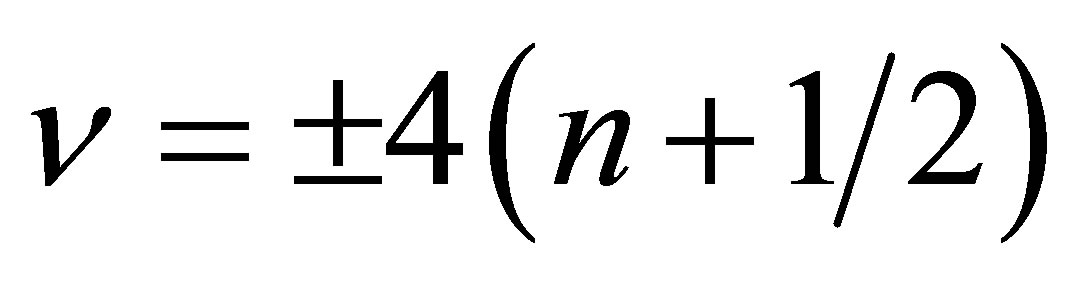 , or for
, or for 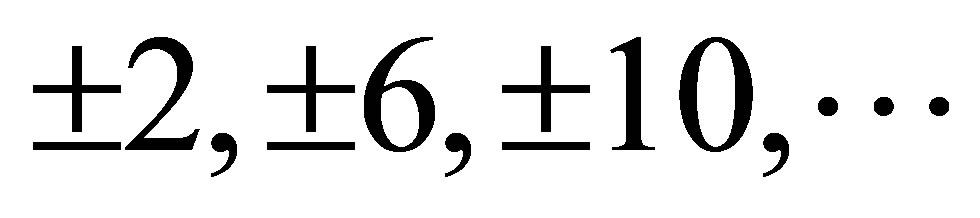 and at zero Landau level in the Dirac point, i.e., for zero energy;
and at zero Landau level in the Dirac point, i.e., for zero energy;  corresponds to particles and holes, respectively, 4 results from pseudospin/valley degeneration,
corresponds to particles and holes, respectively, 4 results from pseudospin/valley degeneration, 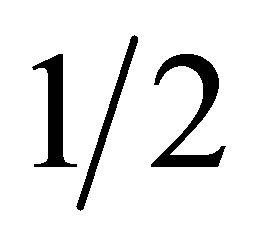 is associated with Berry’s phase for pseudospin) [13,15,16]); cf. Figure 2, which is well-explained by the band structure leading to an effective Dirac description [12,14,15-17]. The Klein paradox, referring to ideal tunneling of Dirac particles through rectangular potential barriers leads to extensive mobility of charge carriers in graphene, which is experimentally observed even near Dirac point (being the Fermi level at the border between electrons and holes if the the gate voltage is not included). In this point, the density of charges is zero (and the zero Landau level is located here, employing both bands) [12,13,15,16].
is associated with Berry’s phase for pseudospin) [13,15,16]); cf. Figure 2, which is well-explained by the band structure leading to an effective Dirac description [12,14,15-17]. The Klein paradox, referring to ideal tunneling of Dirac particles through rectangular potential barriers leads to extensive mobility of charge carriers in graphene, which is experimentally observed even near Dirac point (being the Fermi level at the border between electrons and holes if the the gate voltage is not included). In this point, the density of charges is zero (and the zero Landau level is located here, employing both bands) [12,13,15,16].
The search for states related to the FQHE in the case of the Hall-type measurements in graphene is particularly interesting. Despite using very strong magnetic fields (up to 45 T), FQHE was not detected in graphene samples deposited on a substrate of SiO2 [18]. In [18] it was not-
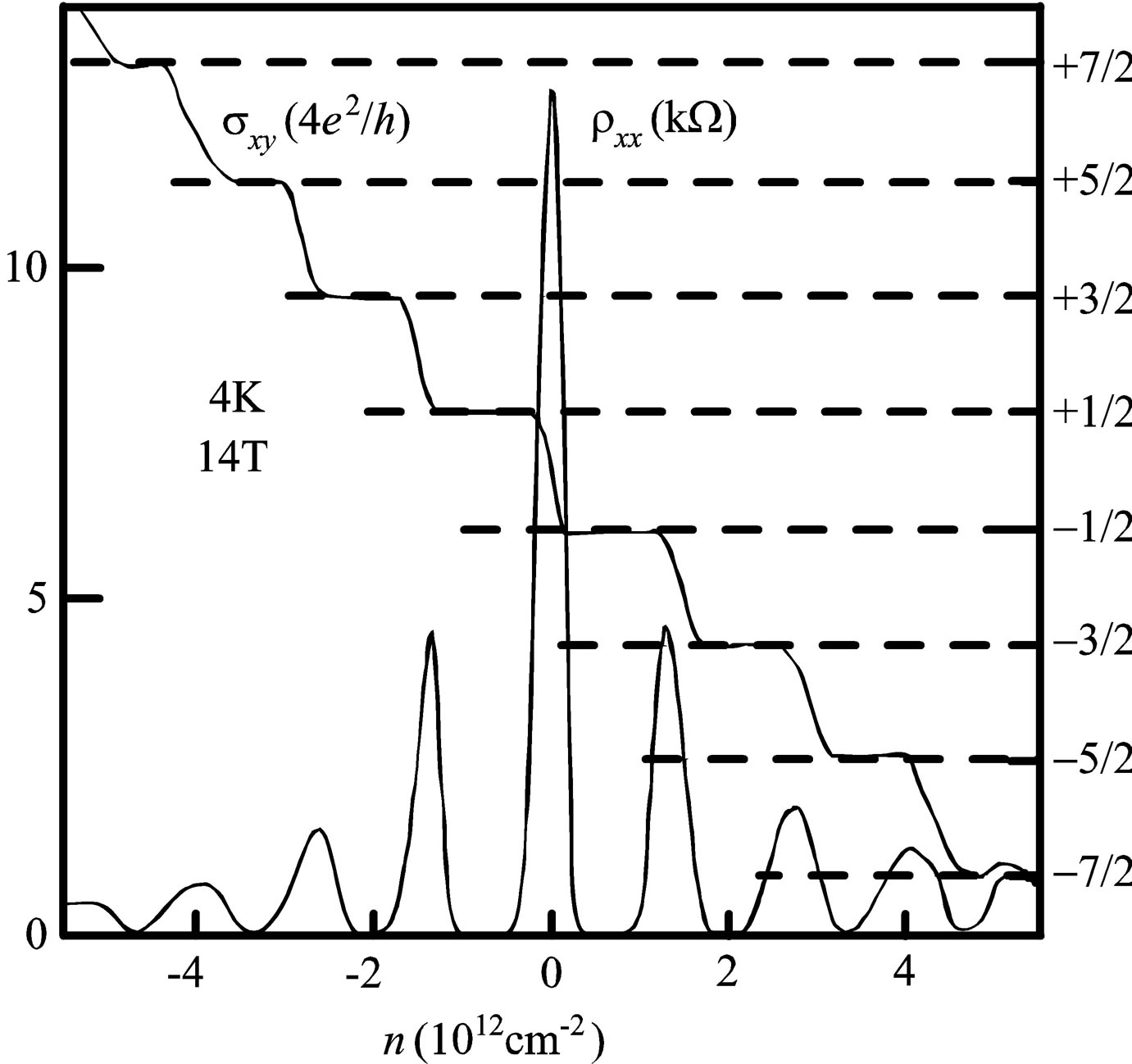
Figure 2. The IQHE in graphene as function of concentration (controlled with lateral gate voltage): the peak for 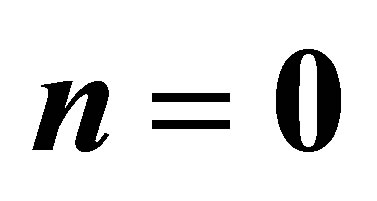 indicates the existence of a Landau level at the Dirac point; electron and hole bands lead to symmetric IQHE oscillation, plateaus
indicates the existence of a Landau level at the Dirac point; electron and hole bands lead to symmetric IQHE oscillation, plateaus 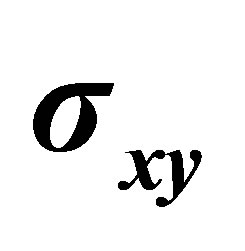 correspond to half multiplicities of
correspond to half multiplicities of 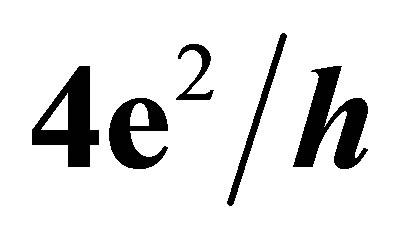 according to the structure of the double-valley pseudospin [Source: A. H. Castro Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov, and A. K. Geim, “The electronic properties of graphene,” Rev. Mod. Phys. 81(1), p. 109, 2009].
according to the structure of the double-valley pseudospin [Source: A. H. Castro Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov, and A. K. Geim, “The electronic properties of graphene,” Rev. Mod. Phys. 81(1), p. 109, 2009].
ed, however, the emergence of additional plateaus of IQHE for the fillings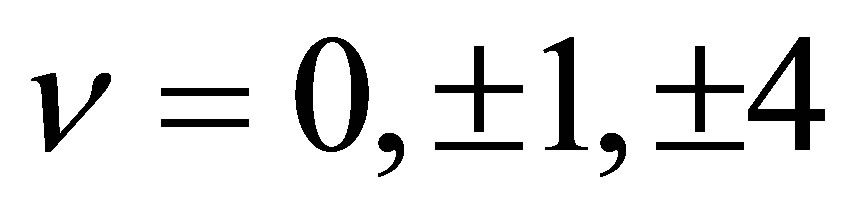 , indicating the elimination of spin-pseudospin degeneration (related to sublattices), as a result of increasing mass of Dirac fermions [18]. Only after mastering the novel technique of the so-called suspended ultrasmall graphene scrapings with extreme purity and high mobility of carriers (beyond 200,000 cm2∙V−1∙s−1; note that high mobility is necessary also to observe the FQHE in the case of semiconductor 2D hetero-structures), it was possible to observe the FQHE in graphene at fillings
, indicating the elimination of spin-pseudospin degeneration (related to sublattices), as a result of increasing mass of Dirac fermions [18]. Only after mastering the novel technique of the so-called suspended ultrasmall graphene scrapings with extreme purity and high mobility of carriers (beyond 200,000 cm2∙V−1∙s−1; note that high mobility is necessary also to observe the FQHE in the case of semiconductor 2D hetero-structures), it was possible to observe the FQHE in graphene at fillings 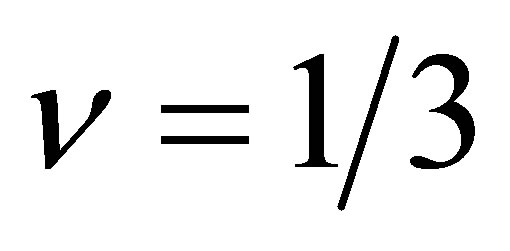 and
and 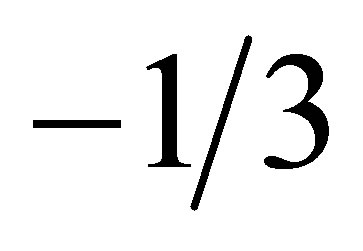 (the latter for holes, with opposite polarization of the gate voltage, which determines position of the Fermi level, either in the conduction band, or in the valence band) [9,10]. Both papers report the observation of the FQHE in graphene for strong magnetic fields. In the paper [10] in a field of 14 T, for electron concentration of 1011 cm2 and in the paper [9] in a field of 2 T, but for smaller concentration by one order Figure 3.
(the latter for holes, with opposite polarization of the gate voltage, which determines position of the Fermi level, either in the conduction band, or in the valence band) [9,10]. Both papers report the observation of the FQHE in graphene for strong magnetic fields. In the paper [10] in a field of 14 T, for electron concentration of 1011 cm2 and in the paper [9] in a field of 2 T, but for smaller concentration by one order Figure 3.
The FQHE in suspended graphene has been observed at the temperatures around 10 K [19] and even at higher temperature (up to 20 K) [20]. Authors have argued that the critical temperature elevation is related to the stronger electric interaction caused by the lack of a dielectric substrate (with a relatively high dielectric constant of solid substrate, $\sim 10$) in the case of suspended samples. However, some other aspects that are likely more important here would be the higher mobility of carriers in the suspended sample (with suppressed acoustic phonon interaction in the ideal 2D system in comparison to influence of 3D solid substrate) and, on the other hand, with very high cyclotron energy in graphene (i.e., the large energy gap between the incompressible states).
In the papers [16,17] the competition between the FQHE state with the insulator state near the Dirac point has also been demonstrated by decreasing carrier concentration—Figure 4. The most intriguing observation is that one [9] indicating an influence of annealing—in Figure 4(b) it is shown that FQHE occurs in the same sample originally insulating but after the annealing process enhancing mobility of carriers due to the pollution reducing. This experiment directly demonstrates the triggering role of carriers mobility in FQHE state arrangement.
3. Quasiclassical Quantization of the Magnetic Field Flux for Composite Fermions
The topological argumentation related to 2D charged multiparticle systems at the presence of strong magnetic field was developed earlier in [21,22]. The main points are as follows:
Ÿ For fractional fillings of the LLL classical cyclotron orbits are too short for particle exchanges (as in the 2D case the long range helical motion is impossible);
Ÿ Nevertheless, the exchanges are necessary to create a collective state such as for FQHE—thus the cyclotron radius must be enhanced (in the model of Jain’s CFs [6] this enhancement is achieved by the artificial addition of flux tubes directed oppositely to the external field; in the model of Read’s vortices [23], reduction of the cyclotron radius is attained by the depletion of the local charge density);
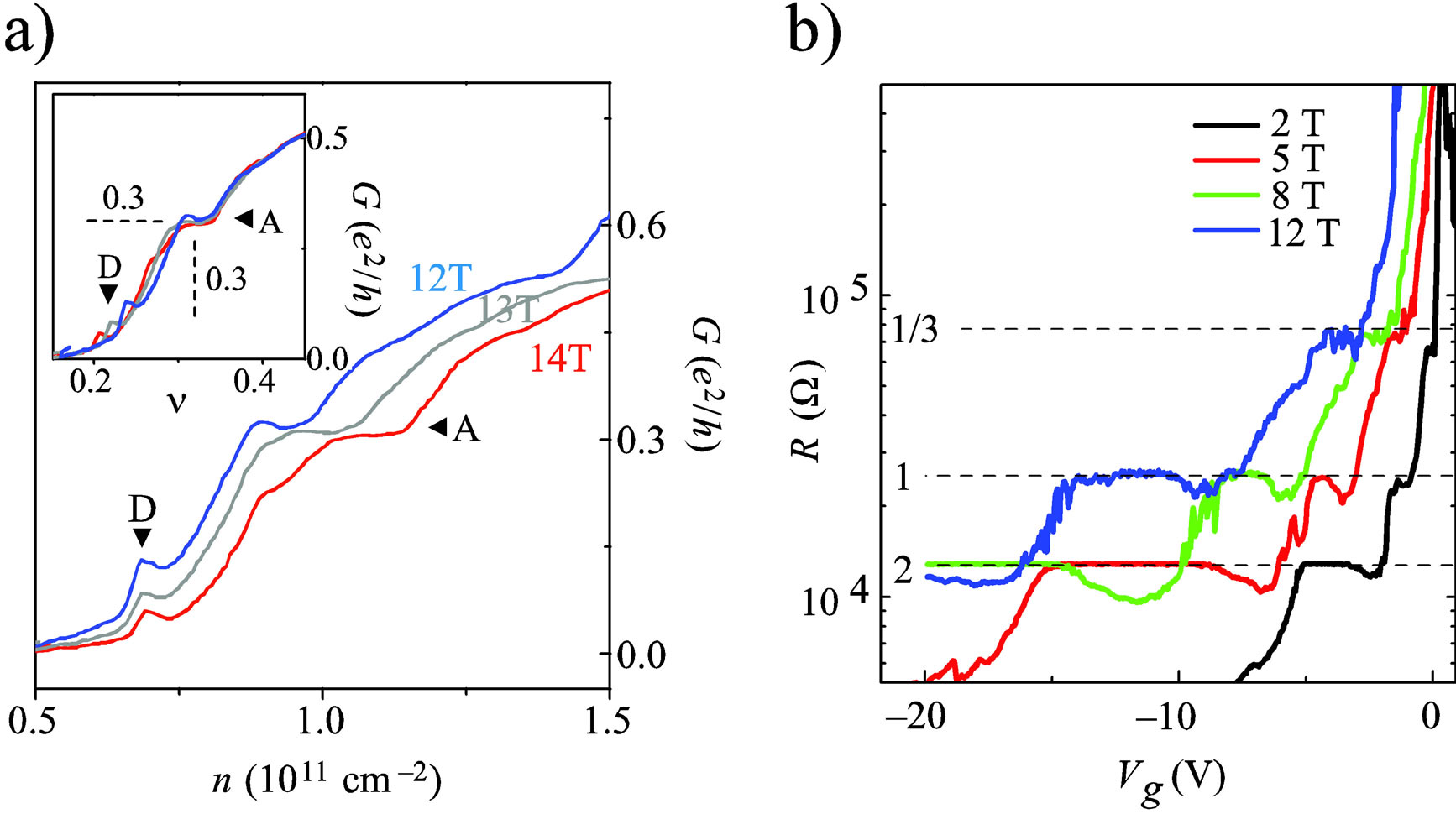
Figure 3. (a) FQHE observed in suspended graphene for the filling 0.3 (1/3) in a field of 12 - 14 T with the concentration of 1011 cm−2 and the mobility of 250,000 cm2∙V−1∙s−1; (b) FQHE singularities in suspended graphene for the filling 1/3 in a field of 2 - 12 T with the concentration of 1010cm-2 and the mobility of 200,000 cm2∙V−1∙s−1 [Source: (a) X. Du, I. Skachko, F. Duerr, A. Liucan, and E. Y. Andrei, “Fractional quantum Hall effect and insulating phase of Dirac electrons in graphene,” Nature 462, p. 192, 2009; (b) K. I. Bolotin, F. Ghahari, M. D. Shulman, H. L. Störmer, and P. Kim, “Observation of the fractional quantum Hall effect in graphene,” Nature 462, p. 196, 2009].
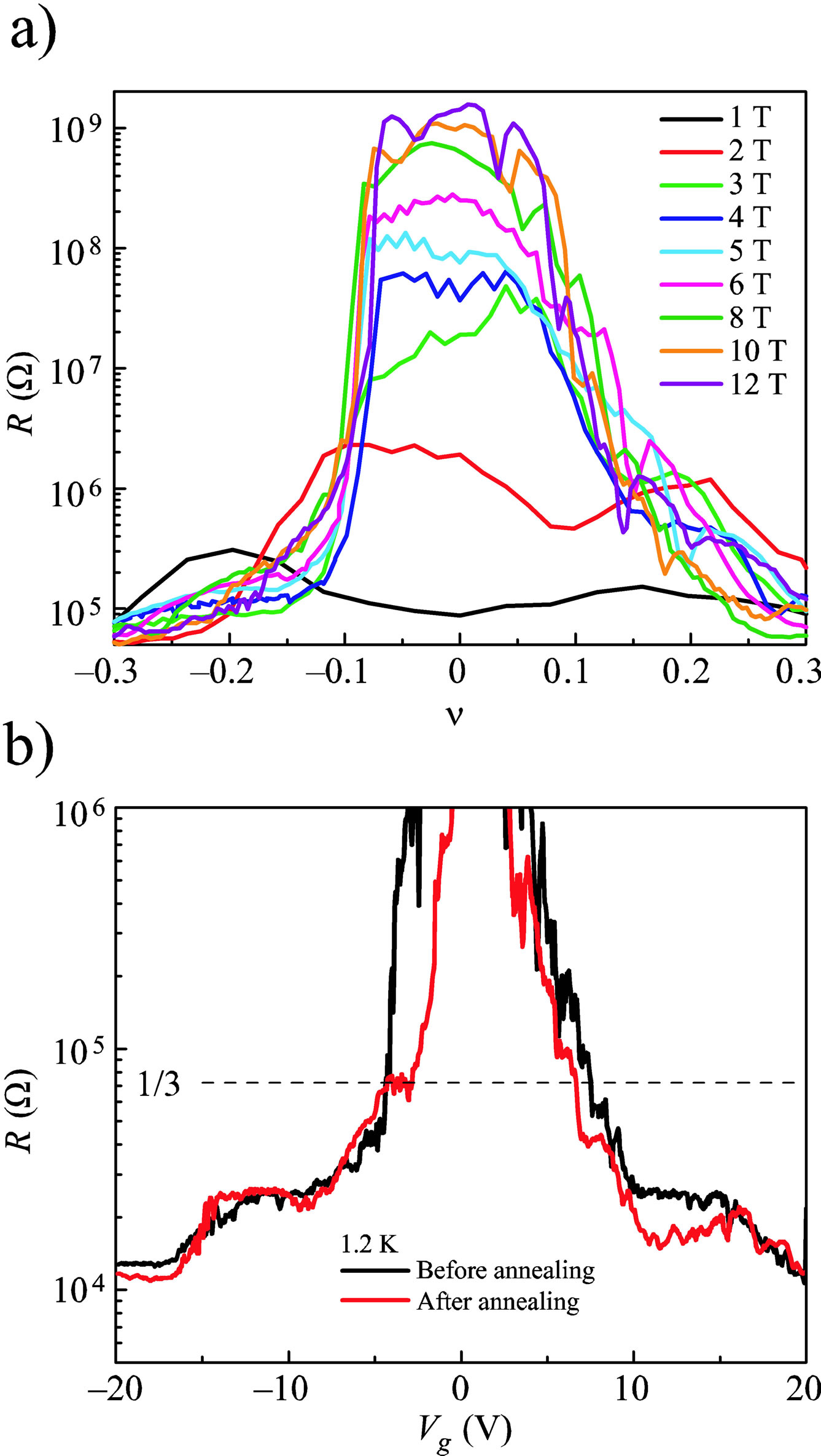
Figure 4. (a) The emergence of an insulator state accompanying the increase in the strength of a magnetic field around the Dirac point; (b) Competition between the FQHE and the insulator state for the filling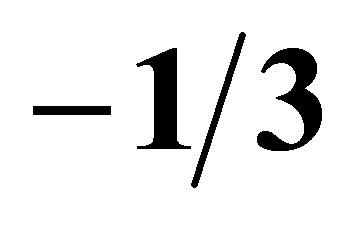 : annealing removes pollution which enhances the mobility and provides conditions for the emergence of a plateau for the FQHE. [Source: K. I. Bolotin, F. Ghahari, M. D. Shulman, H. L. Störmer, and P. Kim, “Observation of the fractional quantum Hall effect in graphene,” Nature 462, p. 196, 2009].
: annealing removes pollution which enhances the mobility and provides conditions for the emergence of a plateau for the FQHE. [Source: K. I. Bolotin, F. Ghahari, M. D. Shulman, H. L. Störmer, and P. Kim, “Observation of the fractional quantum Hall effect in graphene,” Nature 462, p. 196, 2009].
Ÿ The topologically justified way to enhance cyclotron radius consists in the utilizing of multi-looped cyclotron trajectories related to multi-looped braids that describe elementary particle exchanges in terms of braid groups in the case when single-looped exchanges are too short (the resulting cyclotron braid subgroup is generated by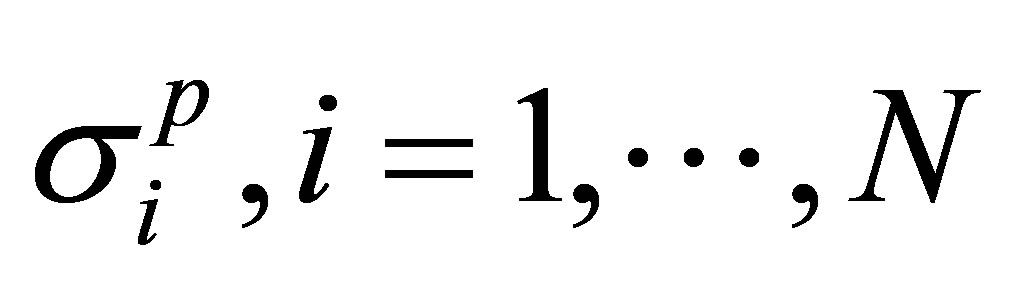 ,
, 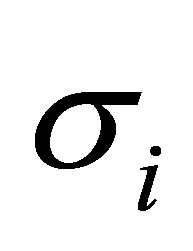 are generators of the full braid group [21,22])—in 2D all loops of multi-looped trajectory must share together the same total external magnetic field flux, in contrast to the 3D case, and this is a reason of enhancement of all loops dimensions effectively fitting to particle separation at LLL fillings
are generators of the full braid group [21,22])—in 2D all loops of multi-looped trajectory must share together the same total external magnetic field flux, in contrast to the 3D case, and this is a reason of enhancement of all loops dimensions effectively fitting to particle separation at LLL fillings , (
, (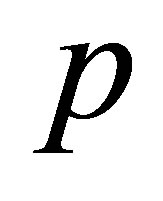 —odd);
—odd);
Ÿ In accordance with the rules of path integration for non-simply-connected configuration spaces [24], one dimensional unitary representations (1DURs) of a corresponding braid group define the statistics of the system—in the case of multi-looped braids, naturally assembled into the cyclotron subgroup [22,25], one arrives in this way at the statistical properties required by the Laughlin correlations (these 1DURs are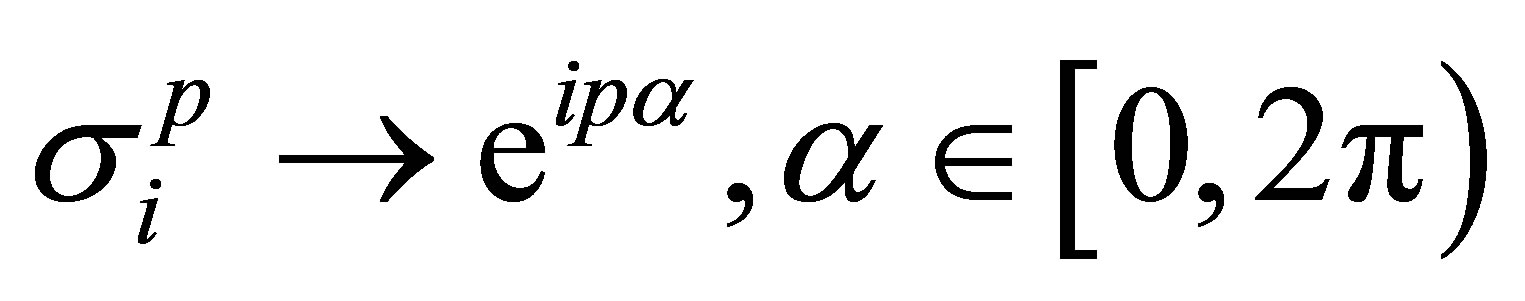 , CFs correspond to
, CFs correspond to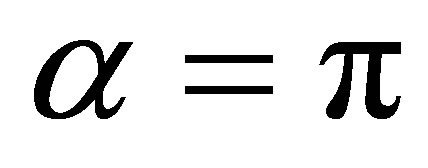 );
);
Ÿ The interaction is crucial for proper determination of the cyclotron braid structure because its short range part prevents the particles from approaching one another closer than the distance given by the density.
This topological argumentation for FQHE statistics does not need to model it by auxiliary elements like flux tubes in CF concept and indicates that CFs are not quasiparticle-type complexes with local fluxes, but are rather quantum 2D particles assigned with Laughlin statistics determined by 1DURs of the appropriate cyclotron braid subgroup.
Even though the auxiliary field flux-tubes fixed to CFs do not exist and only mimic the cyclotron braid structure, they are very useful because of the simplicity of the model and of exploitation of the Chern-Simons field to efficient calculation scheme. Numerical results have indicated the high accuracy of this model, at least for LLL fractional states, but also its convenience in higher LLs. Since the model of CFs with attached rigid flux quanta works so well (as evidenced by the exact diagonalizations), the multi-lopped classical braid structure must be repeated by quasiclassical wave-packet trajectories (and then with quantized fluxes, which was not, however, a rule for classical trajectories). Note that the flux quantization is the quasiclassical property as it needs a trajectory definition and, on the other hand, the carries mobility also has the similar quasiclassical background.
The wave packets corresponding to the quasiclassical dynamics are related to the collective character of a multiparticle system. For LLL of noninteracting system the group velocity of any packet is zero due to degeneration of states (called as ideal band flattening and treated as important prerequisite for FQHE). Interaction removes, however, this degeneracy and provides packet dynamics but the sufficient level of band flattening is still maintained. In general, the collective movement minimizes kinetic energy, whereas the interaction favors localization (localization causes increase in kinetic energy). Therefore, the collective dynamics seems to prefer the quasi-classical movement of packets along periodic closed trajectories (as a rule at the magnetic field presence [26]), which then must, however, embrace quantized external magnetic field fluxes. This emphasizes a significant role for collectivization in the energetic preference of wave packets traversing closed trajectories in correspondence with the classical cyclotron description, including in this way the multi-looped braid picture [22].
These arguments appear to be in accordance with the FQHE observations in graphene (described above), which are found at a low carrier density resulting in some reduction of interaction. This indicates that the interaction is not the sole factor initiating the FQHE formation, as was expected in view of the standard model of composite fermions treating the dressing of fermions with localized flux tubes as a result of just the interaction itself [7,8]. Note that the carrier mobility refers to semiclassical wave packet dynamics in terms of the drift velocity in an electric field and reflects various channels of scattering phenomena beyond the model that includes only Coulomb interaction to free particles in the magnetic field. Impurities and other imperfections of the structure must be included to describe mobility effects. Without going into details of scattering phenomena one can use, however, the topology arguments in the 2D case. High mobility seems to be required for wave packets traversing multi-looped trajectories. Semiclassical wave packets even at presence of interaction and scattering, manifest periodic dynamics [26] and in the case of the multilooped trajectory structure with enhanced radii, a higher mean free path and thus a higher mobility is required, as has been experimentally demonstrated.
4. Cyclotron Braid Group Approach to FQHE in Graphene
From the cyclotron group pont of view, experimental results on FQHE in graphene [9,10,19,20,27] seem to be compliant with the expectations of the braid description. In the case of graphene the control of lateral gate voltage (within the range up to 10 V [10]) allows the regulating of the density of carriers at a constant magnetic field. One should therefore expect that at relatively small densities of carriers (electrons, or symmetrical holes at reverse voltage polarization), the cyclotron orbits will be too short to prevent braid exchanges of particles at a sufficiently strong magnetic field—although weaker for smaller concentrations—and experimental observations have supported this prediction [9,10]. For low concentration, while closing on the Dirac point, one may expect that too strong fields would exceed the stability threshold of the FQHE state in competition with the Wigner crystal (taking into account also a specific character of this competition in the case of massless Dirac fermions in comparison to traditional semiconductor 2D structures, cf. Ref. [28]) and that corresponds to the emergence of the insulating state near the Dirac point in a moderately strong magnetic fields [29]. In the case of the hexagonal structure of graphene, electron (or hole) Wigner crystallization may exhibit interference between the triangular crystal sublattices, and inclusion of the resonance (hopping) between these two sublattices may cause blurring of the sharp transition to the insulator state, which seems to be compliant with observations (Figure 4).
5. Comments
Although the real dynamics of quasiclassical wave packets including and scattering on structure imperfections is beyond the description ability in the framework of a simplified 2D multiparticle charge system upon magnetic field within standard theory of FQHE, some general qualitative conclusions of topological character can be drawn out. In the case of the fractional filling of the LLL, when classical cyclotron orbits are too short for braid exchanges, the multi-looped trajectories occur. Via linkage of this classical cyclotron dynamics in terms of braid group approach with quasiclassical wave packet trajectories, one can expect also multi-looped structure of real quasiclassical wave packet dynamics. With larger radii these multi-looped orbits require longer mean free path and thus favor higher mobility of carriers, and this has been confirmed experimentally in suspended graphene. This suggests that the mobility is of high significance for FQHE formation in competition with localized electron states like insulating Wigner-crystal-type-state. Experiments with graphene have indicated that not only interaction influences stability of FQHE state, which agrees with the topological explanation of CFs properties, thereby demonstrating the triggering role of carrier mobility for Laughlin correlations organization in the multiparticle system.
6. Acknowledgements
Supported by Polish National Center of Science Project no: DEC-2011/02/A/ST3/001.
REFERENCES
- R. B. Laughlin, Physical Review B, Vol. 23, 1981, pp. 5632-5633. http://dx.doi.org/10.1103/PhysRevB.23.5632
- K. von Klitzing, G. Dorda and M. Pepper, Physical Review Letters, Vol. 45, 1980, pp. 494-497. http://dx.doi.org/10.1103/PhysRevLett.45.494
- R. B. Laughlin, Physical Review Letters, Vol. 50, 1983, pp. 1395-1398. http://dx.doi.org/10.1103/PhysRevLett.50.1395
- F. D. M. Haldane, Physical Review Letters, Vol. 51, 1983, pp. 605-608. http://dx.doi.org/10.1103/PhysRevLett.51.605
- R. E. Prange and S. M. Girvin, “The Quantum Hall Effect,” Springer Verlag, New York, 1990. http://dx.doi.org/10.1007/978-1-4612-3350-3
- J. K. Jain, Physical Review Letters, Vol. 63, 1990, pp. 199-202. http://dx.doi.org/10.1103/PhysRevLett.63.199
- O. Heinonen, “Composite Fermions,” World Sc., Singapore, 1998.
- J. K. Jain, “Composite Fermions,” Cambridge UP, Cambridge, 2007. http://dx.doi.org/10.1017/CBO9780511607561
- K. I. Bolotin, F. Ghahari, M. D. Shulman, H. L. Störmer and P. Kim, Nature, Vol. 462, 2009, pp. 196-199. http://dx.doi.org/10.1038/nature08582
- X. Du, I. Skachko, F. Duerr, A. Luican and E. Y. Andrei, Nature, Vol. 462, 2009, pp. 192-195. http://dx.doi.org/10.1038/nature08522
- P. R. Wallace, Physical Review, Vol. 71, 1947, pp. 622- 634. http://dx.doi.org/10.1103/PhysRev.71.622
- A. H. Castro Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov and A. K. Geim, Reviews of Modern Physics, Vol. 81, 2009, pp. 109-162. http://dx.doi.org/10.1103/RevModPhys.81.109
- K. Yang, Solid State Communications, Vol. 143, 2007, pp. 27-32. http://dx.doi.org/10.1016/j.ssc.2007.03.051
- A. K. Geim and A. H. MacDonald, Physics Today, Vol. 8, 2007, p. 35. http://dx.doi.org/10.1063/1.2774096
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, M. I. Katsnelson, I. V. Grigorieva, S. V. Dubonos and A. A. Firsov, Nature, Vol. 438, 2005, pp. 197-200. http://dx.doi.org/10.1038/nature04233
- Y. Zhang, Y-W. Tan, H. L. Störmer and F. Kim, Nature, Vol. 438, 2005, pp. 201-204. http://dx.doi.org/10.1038/nature04235
- J. W. MacClure, Physical Review, Vol. 104, 1956, pp. 666-671. http://dx.doi.org/10.1103/PhysRev.104.666
- Y. Zhang, Z. Jiang, J. P. Small, M. S. Purewal, Y.-W. Tan, M. Fazlollahi, J. D. Chudov, J. A. Jaszczak, H. L. Stormer and P. Kim, Physical Review Letters, Vol. 96, 2006, Article ID: 136806. http://dx.doi.org/10.1103/PhysRevLett.96.136806
- D. A. Abanin, I. Skachko, X. Du, E. Y. Andrei and L. S. Levitov, Physical Review B, Vol. 81, 2010, Article ID: 115410. http://dx.doi.org/10.1103/PhysRevB.81.115410
- I. Skachko, X. Du, F. Duerr, A. Luican, D. A. Abanin, L. S. Levitov and E. Y. Andrei, Philosophical Transactions of the Royal Society A, Vol. 368, 2010, pp. 5403-5416. http://dx.doi.org/10.1098/rsta.2010.0226
- J. Jacak, I. Jóźwiak, and L. Jacak, Physics Letters A, Vol. 374, 2009, pp. 346-350. http://dx.doi.org/10.1016/j.physleta.2009.10.075
- J. Jacak, I. Jóźwiak, L. Jacak and K. Wieczorek, Journal of Physics: Condensed Matter, Vol. 22, 2010, Article ID: 355602. http://dx.doi.org/10.1088/0953-8984/22/35/355602
- N. Read, Semiconductor Science and Technology, Vol. 9, 1994, p. 1859. http://dx.doi.org/10.1088/0268-1242/9/11S/002
- M. G. Laidlaw and C. M DeWitt, Physical Review D, Vol. 3, 1971, pp. 1375-1378. http://dx.doi.org/10.1103/PhysRevD.3.1375
- J. Jacak and L. Jacak, Europhysics Letters, Vol. 92, 2010, Article ID: 60002. http://dx.doi.org/10.1209/0295-5075/92/60002
- P. W. Eliutin and W. D Krivchenkov, “Quantum Mechanics,” Nauka, Moscov, 1976.
- Z. Papić, M. O. Goerbig and N. Regnault, Physical Review Letters, Vol. 105, 2010, Article ID: 176802. http://dx.doi.org/10.1103/PhysRevLett.105.176802
- H. P. Dahal, Y. N. Joglekar, K. S. Bedell and A. V. Balatsky, Physical Review B, Vol. 74, 2006, Article ID: 233405. http://dx.doi.org/10.1103/PhysRevB.74.233405
- C. Yannouleas, I. Romanovsky and U. Landman, Physical Review B, Vol. 82, 2010, Article ID: 125419. http://dx.doi.org/10.1103/PhysRevB.82.125419

