Journal of Modern Physics
Vol. 4 No. 10 (2013) , Article ID: 38872 , 12 pages DOI:10.4236/jmp.2013.410170
Nash Embedding of Witten’s M-Theory and the Hawking-Hartle Quantum Wave of Dark Energy
Department of Physics, Alexandria University, Alexandria, Egypt
Email: Chaossf@aol.com
Copyright © 2013 Mohamed S. El Naschie. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received June 26, 2013; revised July 28, 2013; accepted September 27, 2013
Keywords: Nash Euclidean embedding; quantum entanglement; dark energy of the quantum wave; quantum gravity; ordinary energy of the quantum particle; Hawking-Hartle wave of the cosmos; quantum wave non-demolition; Witten’s M-theory
ABSTRACT
Euclidean embedding of the 11-dimensional M-theory turned out to require a very large space leaving lavish amounts of 242 dimensional pseudo truly empty “regions” devoid of space and time and consequently of anything resembling ordinary physical energy density. It is shown here using Nash embedding that the ratio of “solid” M-theory spacetime to its required embedding “non-spacetime” is  for a classical theory and
for a classical theory and 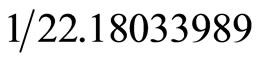 for an analogous fractal theory. This then leads to a maximal ordinary energy density equation equal to that of Einstein’s famous formula
for an analogous fractal theory. This then leads to a maximal ordinary energy density equation equal to that of Einstein’s famous formula  but multiplied with
but multiplied with 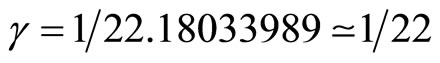 in full agreement with previous results obtained using relatively more conventional methods including running the electromagnetic fine structure constant in the exact solution of the hydrogen atom. Consequently, the new equation corresponds to a quantum relativity theory which unlike Einstein’s original equation gives quantitative predictions which agree perfectly with the cosmological measurements of WMAP and the analysis of certain supernova events. Never the less in our view dark energy also exists being the energy of the quantum wave amounting to 95.5 present of the total Einstein theoretical energy which is blind to any distinction between ordinary energy of the quantum particle and the dark energy of the quantum wave. However, since measurement leads to the collapse of the Hawking-Hartle quantum wave, dark energy being a quantum wave non-ordinary energy could not possibly be measured in the usual way unless highly refined quantum wave non-demolition technology is developed if possible. It is a further reason that dark energy having a different sign to ordinary energy is the cause behind the anti gravity force which is pushing the universe apart and accelerating cosmic expansion. Consequently it can be seen as the result of anticlastic Cartan-like curvature caused by extra compactified dimensions of spacetime. A simple toy model demonstration of the effect of curvature in a “material” space is briefly discussed.
in full agreement with previous results obtained using relatively more conventional methods including running the electromagnetic fine structure constant in the exact solution of the hydrogen atom. Consequently, the new equation corresponds to a quantum relativity theory which unlike Einstein’s original equation gives quantitative predictions which agree perfectly with the cosmological measurements of WMAP and the analysis of certain supernova events. Never the less in our view dark energy also exists being the energy of the quantum wave amounting to 95.5 present of the total Einstein theoretical energy which is blind to any distinction between ordinary energy of the quantum particle and the dark energy of the quantum wave. However, since measurement leads to the collapse of the Hawking-Hartle quantum wave, dark energy being a quantum wave non-ordinary energy could not possibly be measured in the usual way unless highly refined quantum wave non-demolition technology is developed if possible. It is a further reason that dark energy having a different sign to ordinary energy is the cause behind the anti gravity force which is pushing the universe apart and accelerating cosmic expansion. Consequently it can be seen as the result of anticlastic Cartan-like curvature caused by extra compactified dimensions of spacetime. A simple toy model demonstration of the effect of curvature in a “material” space is briefly discussed.
1. Introduction
Nash embedding which is a powerful topological method in the theory of Riemannian manifolds [1-4] is brought to bear on a fundamental and major cutting edge research problem in relativistic quantum cosmology, namely the dark energy of the cosmos [4-8].
The objective of the present work is to gain, using Nash embedding, a better understanding of the deep meaning of two new quantum relativity energy-mass equations [9-18] related to the said subject of the missing dark energy of the cosmos presented in various recent publications [19-25]. The Euclidean embedding space of a manifold, stated in simplistic informal terms, is the space needed to embed a “crumpled” manifold to make it smooth without cusps, discontinuities or overlapping and of course in the simple situation of local embedding makes it Ricci flat [1-3]. Nash embedding [1,2] is a powerful tool based on traditional mathematical methods which gives the exact dimension D(Nash) for an n dimensional manifold to be embedded Euclideanly (see overviews 1 and 2 for a mini introduction to Nash embedding). For a compact manifold this is given by [1,3]
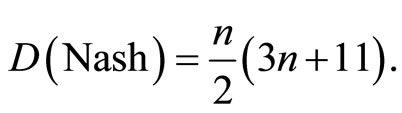 (1)
(1)
As indicated above in the present work we use this formula to gain a deeper insight from a different angle

Overview 1. Missing dark energy resolution via J. Nash Euclidean embedding of compact manifolds.

Overview 2. Deriving E of quantum relativity using isotropy and isomorphic length applied to the geometry and topology of quantum spacetime.
not observed before into two recently derived modified quantum relativity energy formulas extending Einstein’s  [6-18] to:
[6-18] to:
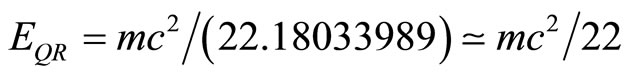 (2a)
(2a)
and
 (2b)
(2b)
where 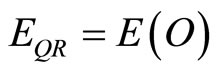 is the ordinary energy which we can measure,
is the ordinary energy which we can measure, 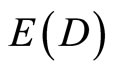 is the dark energy density which we cannot measure directly, m is the mass and c is the speed of light [6,19,20]. Consequently the energy density calculated using EQR is only
is the dark energy density which we cannot measure directly, m is the mass and c is the speed of light [6,19,20]. Consequently the energy density calculated using EQR is only 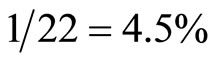 of that calculated using Einstein’s original famous formula [4-6]. This squares perfectly with the data found from numerous accurate cosmological measurements which were rewarded with the 2011 Nobel Prize in Physics [6-8]. On the other hand we know that while the 4.5% measured ordinary energy is the energy of the quantum particle, the rest, i.e. this 95.5% missing dark energy is in fact the energy of the quantum wave given by
of that calculated using Einstein’s original famous formula [4-6]. This squares perfectly with the data found from numerous accurate cosmological measurements which were rewarded with the 2011 Nobel Prize in Physics [6-8]. On the other hand we know that while the 4.5% measured ordinary energy is the energy of the quantum particle, the rest, i.e. this 95.5% missing dark energy is in fact the energy of the quantum wave given by
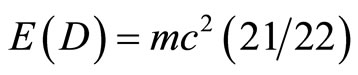 .
.
On the other hand quantum measurement leads to wave collapse [19-23] and consequently the dark energy of the wave cannot be measured by any of present day instruments save for any future progress in quantum wave nondemolition technology [18,23]. Never the less there are many cosmological observations such as the increased rate in cosmic expansion which leads us to believe that dark energy really exists [7,8].
We start here by giving first some relevant applications of Nash’s embedding formula [1,2] and proceed from there to derive the above mentioned quantum relativity formula as well as the quantum relativistic formula for dark energy. We conclude by discussing the relation between dark energy and the measurement problem of quantum mechanics as well as the experimental status of the subject. The Results are conveniently summarized in Figures 1, 2 as well as Table 1 and Overviews 1-3.
2. Nash Embedding Formula and Its Transfinite (Fractal) Extension
To demonstrate the extreme usefulness of Nash’s embedding formula as applied to spacetime physics [1-3] we look at an unconventional application to a generic 3D-like fractal manifold namely the Menger sponge [9,10]. The Hausdorff dimension of this fractal is well known to be [11]
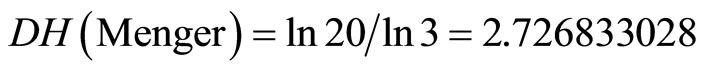 . (3)
. (3)
Taking n to be DH and inserting in Nash formula we find [10,11]
 (4)
(4)
Notice how close this value is to the dimensionality of bosonic strings of the Veneziano-Nambu model for strong interaction [4,12]. The next example is even more interesting as it can be used to make the fundamentality of the four dimensionality of spacetime and its intimate connection to Cantor sets plausible [15]. To do this however we need to extend Nash’s formula by replacing the factor 11 by the self similar eleven [13,14]
 (5)
(5)
where
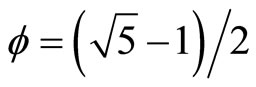 .
.
That way the fractal Nash formula becomes [15]
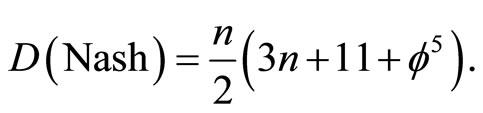 (6)
(6)
Setting 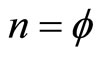 which is the Hausdorff dimension of a Mauldin-Williams random triadic Cantor set [9-11] one finds [15]
which is the Hausdorff dimension of a Mauldin-Williams random triadic Cantor set [9-11] one finds [15]
 (7)
(7)
This is the exact topological dimension of Einstein’s spacetime. In the next section we will apply the original and the modified and extended fractal Nash formula [15] to the eleven spacetime manifold of Witten’s M-theory as well as its fractal counterpart [13,14].
3. Embedding the Spacetime Manifold of M-Theory Euclideanly (See Also Overview 1)
Since Witten’s M-theory [13,14,16] was able in one stroke to unify all the five known superstring theories [13,14,16], it is highly interesting to calculate the dimensionality of the manifold which is required to embed the eleven dimensional manifold of this theory. Setting n = 11 in Nash’s original formula one finds
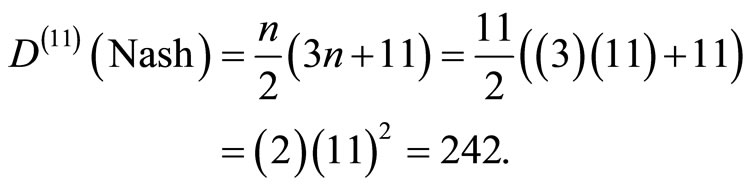 (8)
(8)
Thus a lavishly spacious 242 dimensional manifold is what Nash’s formula grants Witten’s 11 dimensional spacetime [16]. In the case of fractal M-theory D (Nash)
 (a)
(a)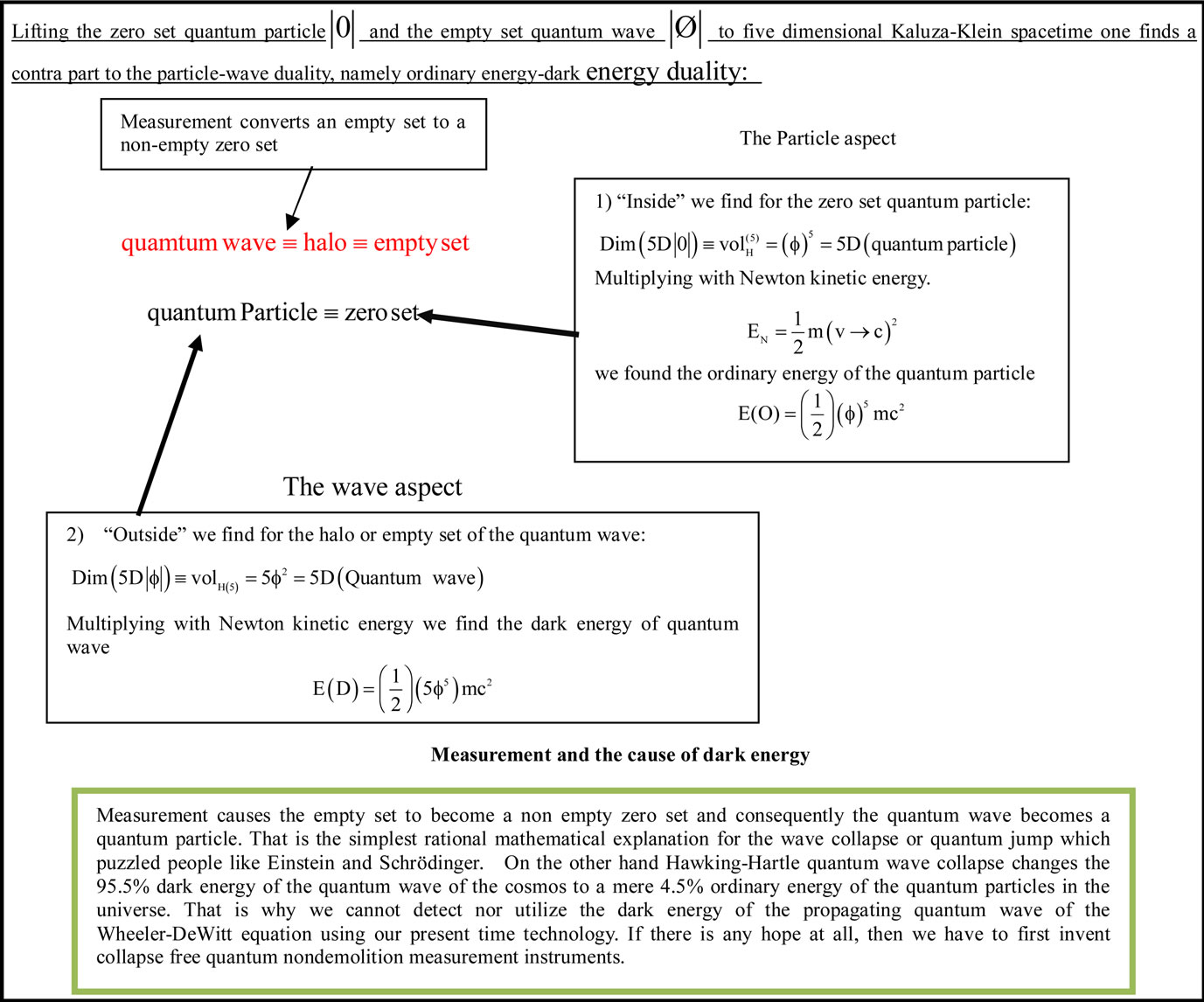 (b)
(b)
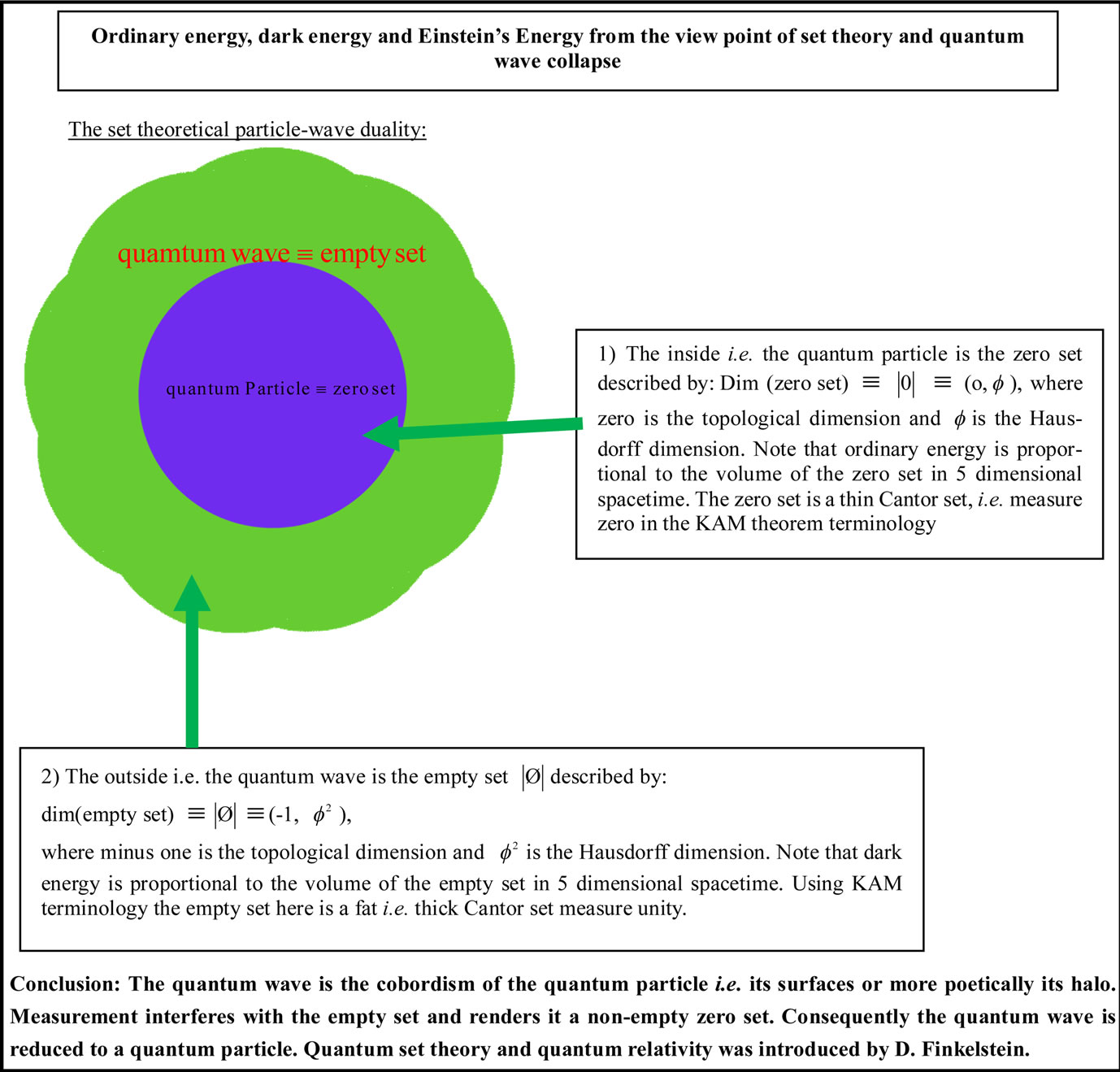
Figure 1. (a) Transfinite set theoretical formulation of particle-wave duality of quantum physics; (b) Quantum entanglement, measurement and the energy of the quantum wave.

Table 1. The reader is reminded again of the basic similarity between compactified extra dimensions and Nash embedding dimensions and halo pseudo energy and negative gravity.
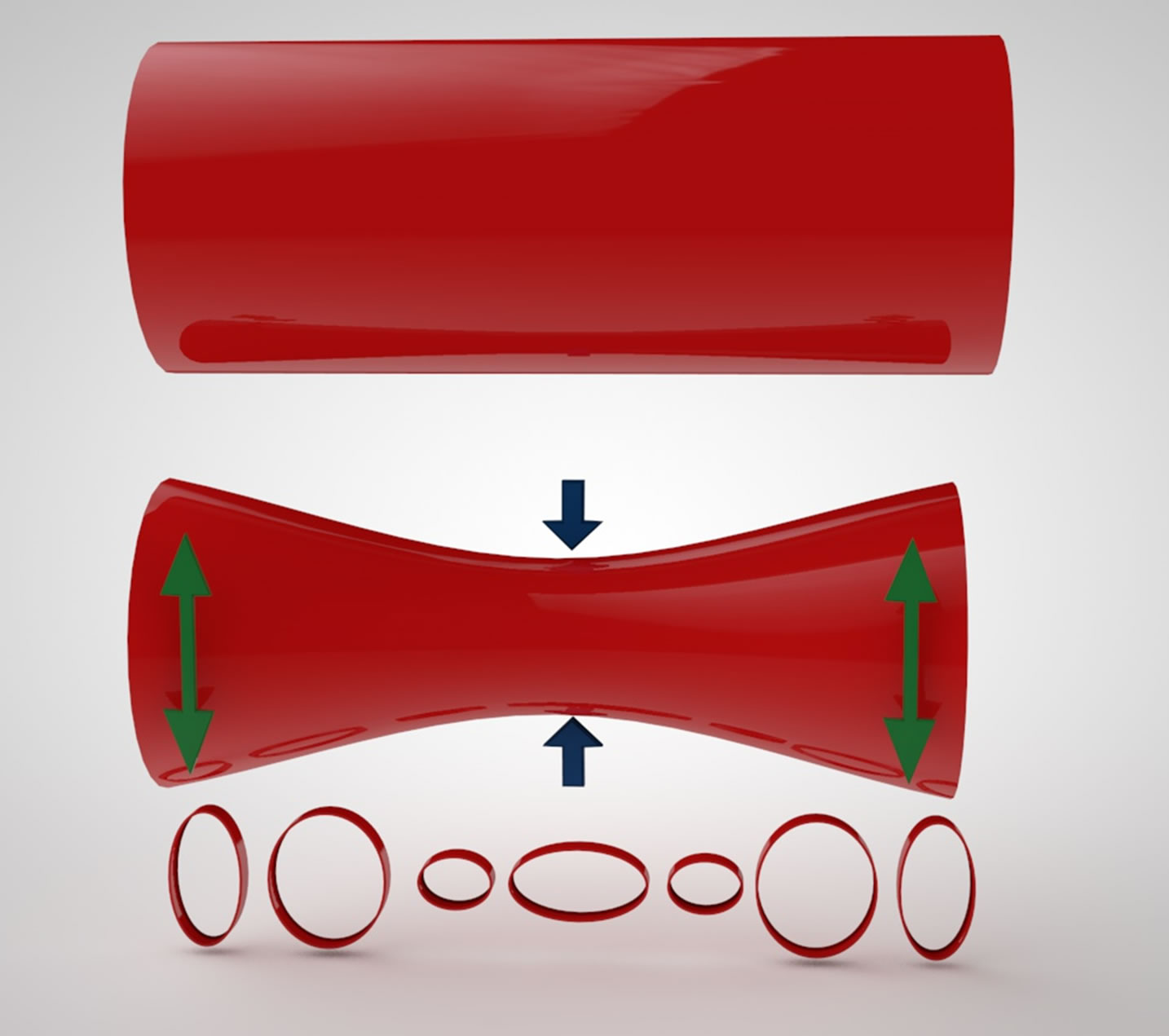
Figure 2. A simple demonstration indicating an analogy to negative curvature and anti gravity. By squeezing a real material space in the form of a long elastic cylindrical tube in the middle, the circular cross-section becomes oval shaped. However this is only in the middle but as we move towards the far end of the cylinder, the oval cross-section rotates and takes a perpendicular position at the edge (see explanation in the main text, paragraph 7).
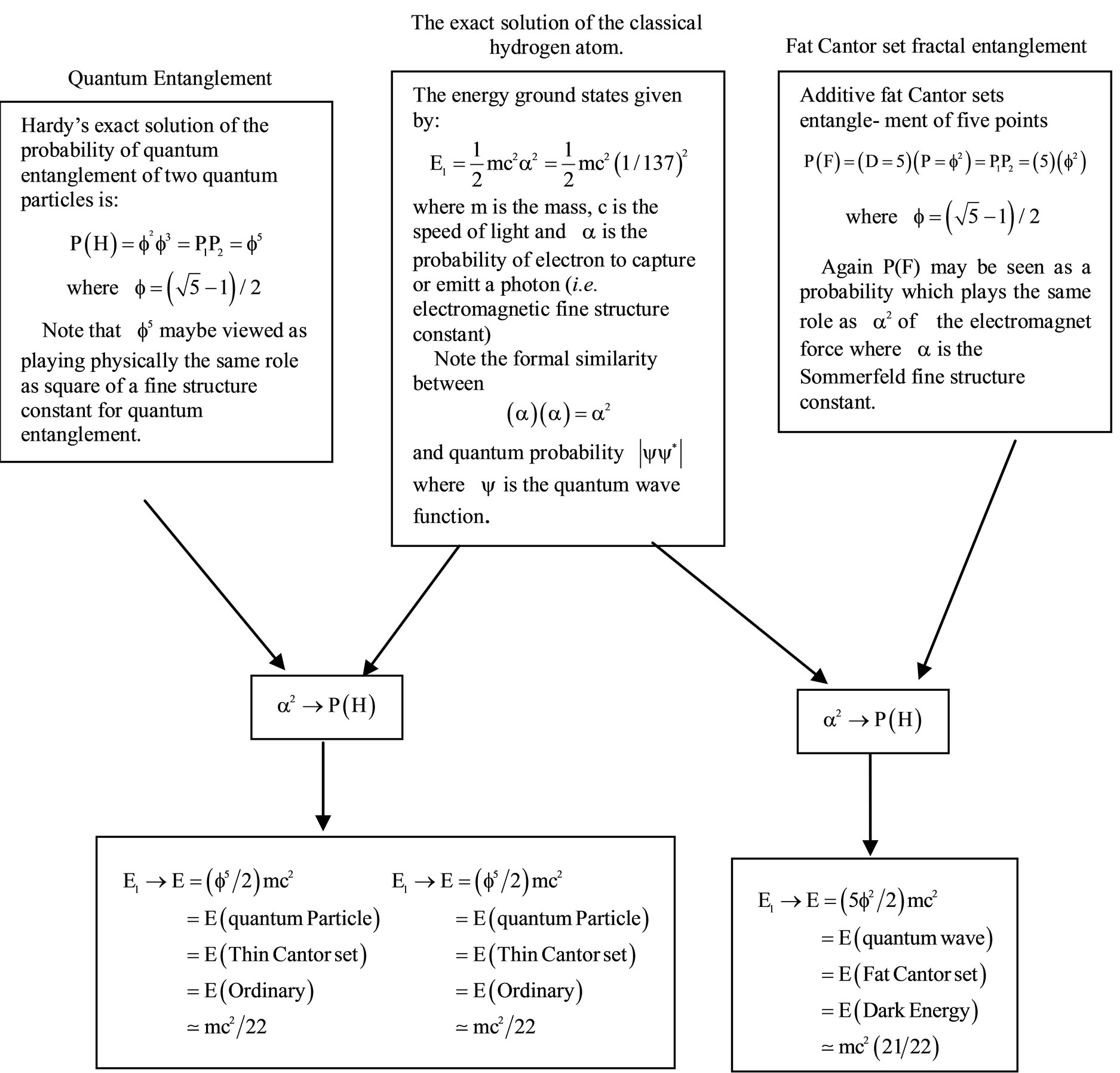
Overview 3. Deriving ordinary energy and dark energy from the ground state energy of the hydrogen atom.
obviously becomes
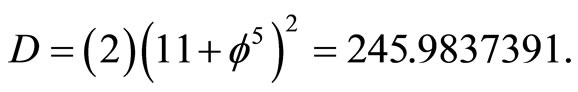 (9)
(9)
We notice that
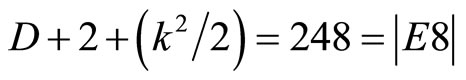 (10)
(10)
where
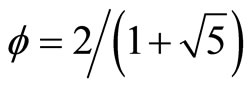

and E8 is the exceptional Lie symmetry group of rank 8 [9,11,12]. (More interesting relations in condensed form are given in Table 1 and Overviews 1, 2). In the next section we will examine the great relevance of the preceding embedding of the eleven dimensional M-theory for quantum relativity and the true meaning of dark energy [6-8].
4. Quantum Relativity EQR and Dark Energy from Nash Embedding of M-Theory
From the preceding section we note that the 11 dimensions of Witten’s M-theory required a 242 dimensions embedding manifold. Consequently the sparseness ratio is easily found as
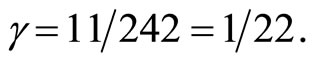 (11)
(11)
This sparseness is what is needed to convert Einstein’s smooth and continuous spacetime to a spacetime invested with voids which contain neither space nor time (see Table 1). Thus looking at 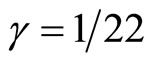 not only as a sparseness factor but also as a Weyl-Nottale scaling exponent we can use
not only as a sparseness factor but also as a Weyl-Nottale scaling exponent we can use 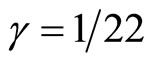 to scale Einstein’s original equation
to scale Einstein’s original equation 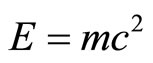 to a relatively new equation [6,19,20]
to a relatively new equation [6,19,20]
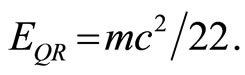 (12)
(12)
Noting that
 (13)
(13)
it becomes evident that dark energy is a consequence of the spacetime voids mentioned above and
 (14)
(14)
which agrees excellently with cosmological data [6,19,20,23]. We note that the same result may be obtained using isotropy and isomorphic length as discussed in Overview 2. In the next paragraph we show that 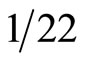 may be viewed as accounting for the effects of quantum entanglement which Einstein rejected and labelled spooky action at distance and therefore did not include it in his derivation even after knowing about it [4,15-19]. A validation of the preceding result is easily obtained using the more conventional method of running the electromagnetic fine structure constant
may be viewed as accounting for the effects of quantum entanglement which Einstein rejected and labelled spooky action at distance and therefore did not include it in his derivation even after knowing about it [4,15-19]. A validation of the preceding result is easily obtained using the more conventional method of running the electromagnetic fine structure constant  in the exact solution of the hydrogen atom and replacing
in the exact solution of the hydrogen atom and replacing  by
by 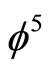 [3] as given in a concise form in Overview 3.
[3] as given in a concise form in Overview 3.
5. The Quantum Entanglement behind Dark Energy
We recall that for the 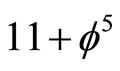 fractal M-theory, D(Nash) was found to be
fractal M-theory, D(Nash) was found to be 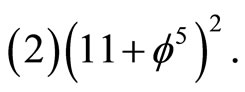 Consequently our sparseness or scaling factor is now
Consequently our sparseness or scaling factor is now
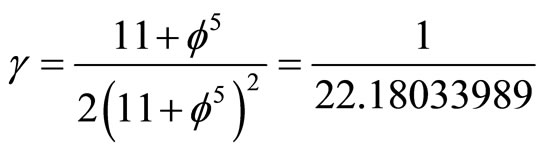 (15)
(15)
and the corresponding energy density is [6]
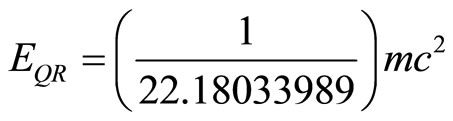 . (16)
. (16)
Noting that
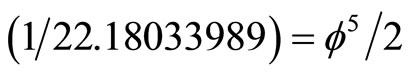 (17)
(17)
where
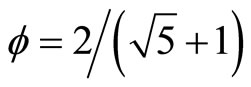 while
while 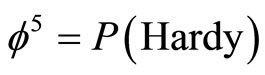
is the well known exact Hardy probability of the quantum entanglement of two quantum particles [17], we see that 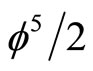 must be the same type of quantum entanglement for a single quantum particle. It follows then that [6,23]
must be the same type of quantum entanglement for a single quantum particle. It follows then that [6,23]
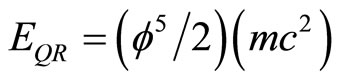 (18)
(18)
is the intersection of relativity and quantum mechanics and we are fully justified in calling this relatively new formula a quantum relativity formula which is expected to hold true for extremely small as well as extremely large distances because there is no meaning for space separation in quantum entanglement [4,6-8]. The agreement with cosmological measurement [6-8] reconfirms this expectation beyond any reasonable doubt [7,8,19].
6. Wave-Particle Duality, Measurement and Dark Energy
We have established in previous work that 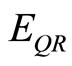 s the energy density of the quantum particle modelled by the zero set
s the energy density of the quantum particle modelled by the zero set 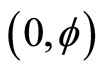 in five dimensional Kaluza-Klein spacetime [24-26]
in five dimensional Kaluza-Klein spacetime [24-26]
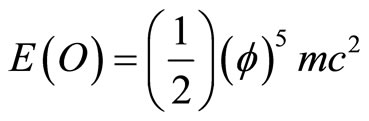 (see Figure 1).
(see Figure 1).
The complementary energy of  is the dark energy density
is the dark energy density 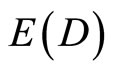 as modelled by the empty set
as modelled by the empty set 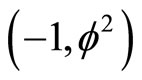 in the same K-K five dimensional spacetime and corresponding to the energy of the quantum wave which amounts to
in the same K-K five dimensional spacetime and corresponding to the energy of the quantum wave which amounts to
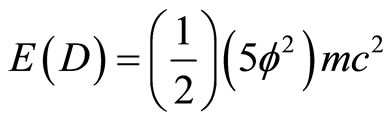
as shown in Figures 1(a) and 1(b). Three extremely important conclusions with far reaching consequences for science and technology are reconfirmed from the above.
The first is that
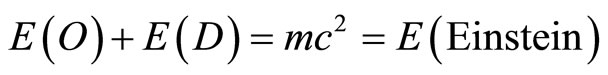
and therefore we can say that Einstein’s formula is basically exact with the only drawback that it does not distinguish between the ordinary energy of the quantum particle and the dark energy of the quantum wave which cannot be measured [18-21,23].
The second conclusion is that our inability to measure the dark energy of the Hawking-Hartle quantum wave of the universe using our present technology is clearly connected to the quantum measurement problem and the well documented quantum wave collapse. In other words dark energy could be in principle detected and even utilized nuclear in reactors if we could develop collapse free nondemolition measurement instruments [22]. Only future technological developments could settle this problem which seems at present to be out of reach [18]. The third and final conclusion is that dark energy is related to negative curvature of spacetime and its most outer edges. Such negative curvature which gives rise to negative gravity arises naturally in granular spacetime geometry as in our case [27-29]. To show that we recall the result of Heterotic string theory with 504 particle-like states [30] compared to the 528 five dimensional Brans in 11 dimensions [29]. The ratio is exactly that of the dark energy factor 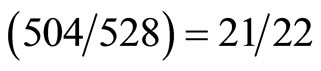 which is approximately
which is approximately 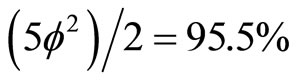 as reasoned earlier on. Thus like electromagnetism, strong-weak force gravity is positive and negative. In this connection we stress the importance of what P. Wesson named five dimensional physics [26]. The view point expressed here as well as in [26] were developed without any knowledge of [26] but never the less is remarkably pointing in the same direction.
as reasoned earlier on. Thus like electromagnetism, strong-weak force gravity is positive and negative. In this connection we stress the importance of what P. Wesson named five dimensional physics [26]. The view point expressed here as well as in [26] were developed without any knowledge of [26] but never the less is remarkably pointing in the same direction.
7. Antigravity Toy Model Demonstrating the Action-Reaction Nature of Curvature-Anti-Curvature via a Simple Long Quasi Elastic Paper Tube Equations
There is a charmingly simple toy model to mimic antigravity which is easily made by rolling a sheet of high quality writing paper into a long tube. In Figure 2 it is demonstrated that squeezing the tube in the middle deforms its circular cross-section into an oval form which results, with increasing distance towards the edges, in a rotation of the oval cross-section with the maximal oval deformation at the two ends and the two axes of the elliptic crosssection perpendicular to the oval in the middle. The point is that the differential geometry of the real paper cylinder, i.e. a material space with a Poisson’s ratio [27] is fundamentally different from the simple rudimentary differential geometry of “mathematical” Euclidean space of Newton and the theoretical idealized continuous spacetime of Einstein’s relativity whether curved as in general relativity or flat as in special relativity. Looking forward to generalize from this admittedly simple model we can see that we have the possibility for a more realistic geometry of a granule-like quantized atom spacetime or a spacetime with very large dimensionality like for instance the Lie manifold with 496 dimensions corresponding to E8E8 exceptional Lie symmetry groups of superstrings [12] in which we have Cartan-like torsion and Cosserat-like rotation of a micro polar media, i.e. a kind of non-Boltzmannian theory of elasticity [27,28]. In such “more realistic” geometry and topology we see that a local action causing a curvature can provoke a remote reaction as far as at the end of the universe producing anti-curvature and thus antigravity prompting the observed increased rate of cosmic expansion. That way we bring gravity in line with the rest of the fundamental forces, i.e. attracting and repelling form of each force. Now we could give a very simple formula for determining the effect of curvature on antigravity and thus dark energy using a heuristic methodology.
We start with a maximally symmetric manifold, namely that of Witten-Duff five Brans in eleven dimensions [29,30]. The number of dimensions of the manifold is equivalent to the number of killing vector fields. This is given by the same well known formula of dim SO(n), namely [4]
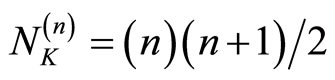 . (19)
. (19)
For 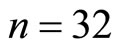 one finds the famous 528 [24]
one finds the famous 528 [24]
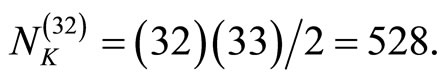 (20)
(20)
From these 528 we have the Heterotic superstrings theory 504 particle-like states running in one direction [30] leaving 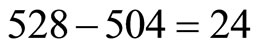 running in the opposite direction. Thus the percentage of the 24 from the 528 total is exactly
running in the opposite direction. Thus the percentage of the 24 from the 528 total is exactly
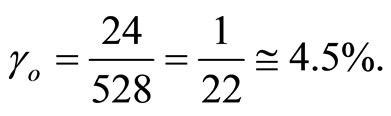 (21)
(21)
which is the density of ordinary energy of the quantum particle previously obtained using various other methods [20,24,25,28]. The other energy as we will see is the dark energy and is clearly given by
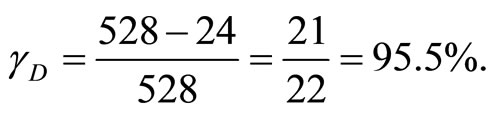 (22)
(22)
exactly as expected. Our Lorentz-like parameter of antigravity  is consequently the ratio between Cartanlike curvature components constituting non-Boltzmannian shear or nonclassical curvature components similar to that appearing in non-Boltzmannian elasticity or in the deformation of our simple paper toy model (Figure 2). It follows then that our understanding of
is consequently the ratio between Cartanlike curvature components constituting non-Boltzmannian shear or nonclassical curvature components similar to that appearing in non-Boltzmannian elasticity or in the deformation of our simple paper toy model (Figure 2). It follows then that our understanding of 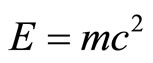 should be revised to being the sum of two different energies [20]. The first is the ordinary energy of the quantum particle given by [23,25]
should be revised to being the sum of two different energies [20]. The first is the ordinary energy of the quantum particle given by [23,25]
 (23)
(23)
while the second is the dark energy of the quantum wave [23,25]
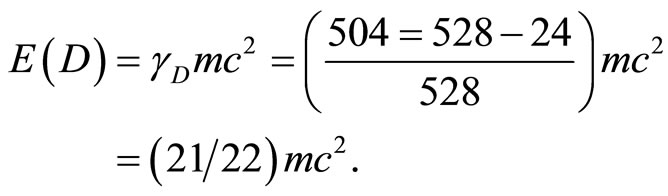 (24)
(24)
Consequently we have
 (25)
(25)
Furthermore we must note and initially also heuristically, that 21 is 26 – 5 where 26 are the bosonic string dimensions of theoretical Veneziano’s model of strong interactions while 5 is the dimensionality of KaluzaKlein unification spacetime of gravity and electromagnetism [26] and 4 is the spacetime dimensionality of Einstein’s gravity. Consequently 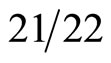 could be interpreted as a parameter for dark energy density of the quantum wave
could be interpreted as a parameter for dark energy density of the quantum wave
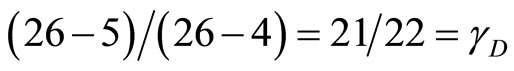
while

is the corresponding parameter for the quantum particle.
Let us give for 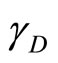 of dark energy a more general derivation which we feel some readers may find more profound and convincing. We start with the Bulk according to all superstring theories [12] which is given by
of dark energy a more general derivation which we feel some readers may find more profound and convincing. We start with the Bulk according to all superstring theories [12] which is given by
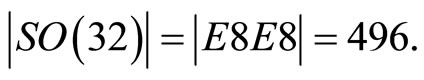
Now we are definitely right to think that 12 of these massless gauge bosons of the first point of departure were used in deriving the ordinary energy related to 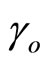 and consequently for dark energy we have
and consequently for dark energy we have
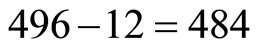
massless gauge bosons still left at our disposal. On the other hand what neither the 4 dimensional Einstein theory nor any modification of it has taken into account is definitely the five dimensional Branes particle-like states of Duff, Witten and Randal [4,16,29]. From the total of 528 killing vector fields equal to the total number of states in Witten-Duff model we have 11 one dimensional objects, 55 two dimensional particle-like states and thus 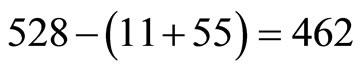 five dimensional Branes. The ratio between these 462 and the total left from 496, i.e. the 484 gauge bosons is what gives us the density of the dark energy factor
five dimensional Branes. The ratio between these 462 and the total left from 496, i.e. the 484 gauge bosons is what gives us the density of the dark energy factor 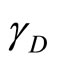 which is sure enough the expected value [20,23]
which is sure enough the expected value [20,23]
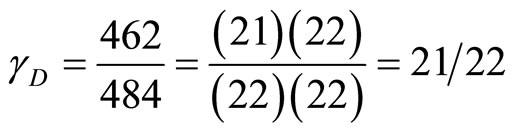 . (26)
. (26)
The preceding analysis could be made transfinitely exact by noting the following transfinite replacements which were explained in detail elsewhere [9,10]
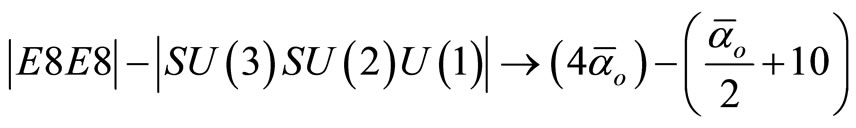 (27)
(27)
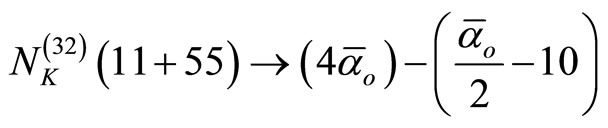 (28)
(28)
where 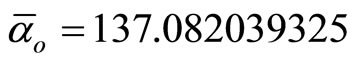 is the theoretical Cantorian value of the inverse electromagnetic fine structure constant and
is the theoretical Cantorian value of the inverse electromagnetic fine structure constant and 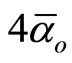 is the exact sum of all the exceptional Lie symmetry groups of Ei-line:
is the exact sum of all the exceptional Lie symmetry groups of Ei-line:
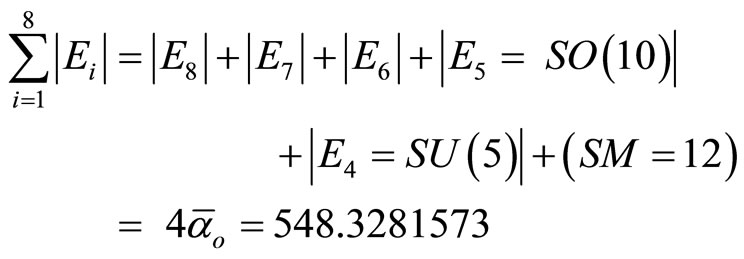 (29)
(29)
where
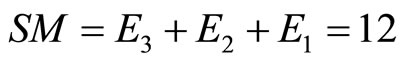
are the 12 massless bosons of the standard model [9-11]. Note that we used in all the above Ei the transfinite exact values. For instance │E8│= 248 is corrected to
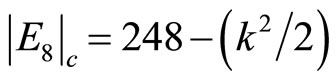
where
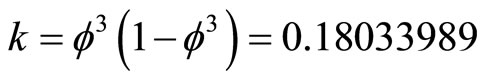 and
and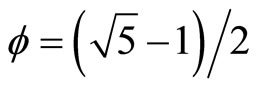 .
.
8. The Current Experimental Status of E = mc2 and Its Quantum Relativity Revision to E(O) = mc2/22 and E(D) = mc2(21/22)
Having made substantial modification to E = mc 2 a few words on the experimental situation are definitely in order at this point. There is a widespread misconception that 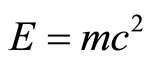 (where E is the maximal energy, m is the rest mass and c is the speed of light) was tested to a very high degree of accuracy and is thus beyond revision. This is far from being an accurate description of the state of affairs regarding this arguably most famous of all equations [4]. In fact the opposite is true and with the benefit of hindsight we can say that it should have been clear from the beginning that most of the experiments conducted purporting to prove that
(where E is the maximal energy, m is the rest mass and c is the speed of light) was tested to a very high degree of accuracy and is thus beyond revision. This is far from being an accurate description of the state of affairs regarding this arguably most famous of all equations [4]. In fact the opposite is true and with the benefit of hindsight we can say that it should have been clear from the beginning that most of the experiments conducted purporting to prove that  are quantum experiments performed under classical and semi-classical assumptions as well as interpretations. A correct interpretation of classical experiments related to the validity of the correspondence principle would long ago have revealed that
are quantum experiments performed under classical and semi-classical assumptions as well as interpretations. A correct interpretation of classical experiments related to the validity of the correspondence principle would long ago have revealed that 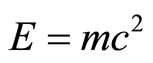 is not the complete story and would have prepared us for the relatively recent results of the COBE, MAP and supernova measurements and analysis and the ensuing introduction of the new concept of dark energy which took all of us with a huge surprise [7,8]. In what follows we list the most obvious experiments which strongly hint at the afore mentioned misconception:
is not the complete story and would have prepared us for the relatively recent results of the COBE, MAP and supernova measurements and analysis and the ensuing introduction of the new concept of dark energy which took all of us with a huge surprise [7,8]. In what follows we list the most obvious experiments which strongly hint at the afore mentioned misconception:
1) The correct interpretation of the famous COW experiment [31] as well as several refined versions of it all indicate a violation of the correspondence principle. Consequently there is no energy formula which can be exact and accurate without involving quantum theory, i.e. without quantum gravity or an effective quantum gravity theory [20].
2) Gravitational quanta were experimentally found, probably for the first time, by a Russian group led by V.V. Nesrizhevsky [32]. This is totally incompatible with a smooth continuous spacetime such as that of relativity and particularly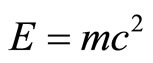 .
.
3) Quantum particles have no path. By contrast all experiments used in verifying E = mc 2 discuss the set up and result in terms of a particle with a path which is a contradiction for an experiment which is aimed at solving a contradiction [9,10].
4) The cosmological measurements which led to the 2011 Nobel Prize in Physics all indicated that at a minimum something is amiss in standard relativity when probing extreme situations such as distances in the order of the Hubble radius [7,8,33].
5) The work of F. Zwiky as well as that of Magueijo, Moffat [34], Milgrom and Beckenstein apart of the flight of the Galileo probe as well as pioneer 10 and pioneer 11 [4,7,8] all show that something is not entirely right in the state of Denmark and as Shakespeare advises us in Hamlet: “There are more things in heaven and earth”. These things we hope we showed to be basically quantum spacetime itself or said a little more conservatively, it is the dark energy of a quantum wave which is devoid not only of matter and momentum but also of ordinary energy which is the privilege of the quantum particle only [20,21,23,25].
9. Discussion and Conclusions
To embed Witten’s eleven dimensional M-theory we require 242 dimensions. The eleven dimensional spacetime of M-theory, if regarded as solid spacetime is thus puffed up to a 242 fractal-like spacetime. It is intuitively obvious that as a measure of the sparseness of this space, the ratio of 11 to 242 equals 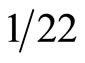 is an excellent characterization of the amount of voids containing no space and no time and which is merely there to simulate Euclidean continuity and smoothness. We conjectured previously that
is an excellent characterization of the amount of voids containing no space and no time and which is merely there to simulate Euclidean continuity and smoothness. We conjectured previously that 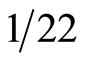 may be regarded as a Weyl-Nottale scaling exponent [6,19] which accounts for the fractal nature of cotton candy-like quantum spacetime and converts the relativistic equation
may be regarded as a Weyl-Nottale scaling exponent [6,19] which accounts for the fractal nature of cotton candy-like quantum spacetime and converts the relativistic equation  into a quantum relativity equation
into a quantum relativity equation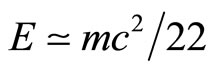 . This new confirmation of a relatively also new equation gives results which agree completely with the cosmological measurement of the cosmic hypothetical dark energy [6-8]. Seen in this way, the missing dark energy of the cosmos is more likely to be not only a missing
. This new confirmation of a relatively also new equation gives results which agree completely with the cosmological measurement of the cosmic hypothetical dark energy [6-8]. Seen in this way, the missing dark energy of the cosmos is more likely to be not only a missing  factor in Einstein’s famous equation [6] but also a fundamental problem of quantum measurement and quantum wave collapse which puzzled people like Einstein and Schrödinger [4,18].
factor in Einstein’s famous equation [6] but also a fundamental problem of quantum measurement and quantum wave collapse which puzzled people like Einstein and Schrödinger [4,18].
We chose in the present work to tackle this problem and argue our case using John Nash’s celebrated formula for Euclidean embedding [1-3]. However there are many other less mathematical ways to convincingly argue the case for 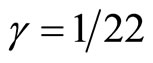 [23]. Here we mention three such simple arguments:
[23]. Here we mention three such simple arguments:
1) It is generally accepted that at least within the theory of strong interaction the bosonic string model reflects a substantial part of physical reality [4]. This model supposes that spacetime is 26 dimensions [4,12]. Consequently Einstein used only 4 of these 26 dimensions. The remaining 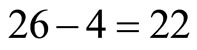 dimensions could be thought of as compactified or dark dimensions [6]. It follows then that if fractal similarity rules the problem and obviously it does rule it, then
dimensions could be thought of as compactified or dark dimensions [6]. It follows then that if fractal similarity rules the problem and obviously it does rule it, then 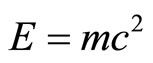 must be multiplied by the scaling exponent
must be multiplied by the scaling exponent 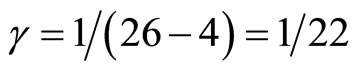 and E becomes
and E becomes 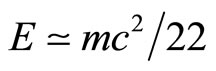 [23].
[23].
2) From a particle physics view point, Einstein’s special relativity may be regarded as a one degree of freedom theory [6]. The photon is that degree of freedom. However the situation changed completely since 1905. We know today that our standard model functions only when 12 photon-like messenger particles are taken into account [4,6]. All these 12 elementary particles were experimentally confirmed and are represented mathematically via the dimensions of the Lie symmetry groups of the standard model [10]:
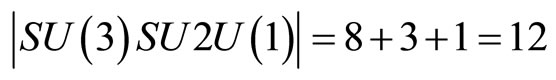 .
.
Consequently special relativity did not take 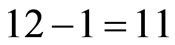 photon-like particles into account. Adding the hypothetical super partners we have (11)(12) = 22 “hidden” particles as far as special relativity is concerned. The Weyl-Nottale scaling factor is yet again our previous one, namely
photon-like particles into account. Adding the hypothetical super partners we have (11)(12) = 22 “hidden” particles as far as special relativity is concerned. The Weyl-Nottale scaling factor is yet again our previous one, namely 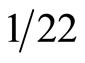 and E is again
and E is again 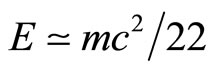 [18-21]. This problem was solved in [24] using a simple Lagrangian and a multiplier.
[18-21]. This problem was solved in [24] using a simple Lagrangian and a multiplier.
3) Running the electromagnetic coupling 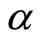 in the ground state of the exact solution of the hydrogen atom by exchanging
in the ground state of the exact solution of the hydrogen atom by exchanging 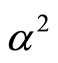 for Hardy’s
for Hardy’s 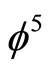 we find
we find  as explained in Overview 3 [33].
as explained in Overview 3 [33].
From the above we clearly see that all methods lead to the same 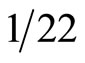 showing that it is a robust result and fairly independent from the fine details of the method or the theory used as long as it is a fairly reasonable theory [6,7]. Never the less this is not nearly the end of the story. Further analysis and digging deeper into the transfinite set theoretical origin of the fabric of spacetime reveals the following startling results [24]:
showing that it is a robust result and fairly independent from the fine details of the method or the theory used as long as it is a fairly reasonable theory [6,7]. Never the less this is not nearly the end of the story. Further analysis and digging deeper into the transfinite set theoretical origin of the fabric of spacetime reveals the following startling results [24]:
4) Ordinary energy and dark energy are but an important facet of the particle wave-duality. The ordinary energy is found to be the energy of the quantum particle in 5 dimensions while the absolute value of dark energy is the opposite sign energy of the quantum wave also in five dimensions [25,26]
5) The sum of the ordinary energy and dark energy density turns out to be exactly equal to Einstein’s energy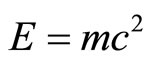 . Consequently Einstein’s theory is exact but it is blind to distinguishing between the ordinary measurable 4.5 percent energy and the 95.5 percent dark energy which we cannot measure directly.
. Consequently Einstein’s theory is exact but it is blind to distinguishing between the ordinary measurable 4.5 percent energy and the 95.5 percent dark energy which we cannot measure directly.
6) Since measurement collapses the quantum wave by turning an empty set into non empty zero set i.e. a zero set quantum particle [20,23], we could not possibly measure the dark energy of that wave until we invent measurements which do not collapse the quantum wave [18]. Such instruments maybe related in one way or another to the ideas of quantum nondemolition measurement pioneered by V. Braginsky [22].
From the preceding points one could speculate on the possibility of a nuclear propagating dark energy reactor which would in theory be at least 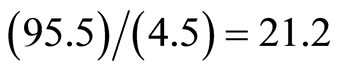 times more efficient than conventional ordinary energy reactors in addition to being possibly safer and harmful radiation free. These are of course exciting possibilities which maybe at present on the demarcation line between science fact and science fiction. We are of course aware of an entire school of research on the foundations of quantum mechanics which may be labelled “Against Measurement”. However we think that there is more reality to measurement and dark energy than we initially thought [23]. For instance it is conceivable from the identity of the mathematical formalism of the quantum wave and that of quantum spacetime itself that these are different labels for what is essentially the same. Seen in this way the Feynmann propagator and the HawkingHartle wave are essentially a multi-fractal quantum spacetime. In such multi fractal real plethora of empty sets modelling spacetime, the speed of light is a variable ranging from zero to infinity while the constant C is only an average expectation value. Consequently our theory is essentially a fractal version of the theories of variable speed of light [23-26,34,35].
times more efficient than conventional ordinary energy reactors in addition to being possibly safer and harmful radiation free. These are of course exciting possibilities which maybe at present on the demarcation line between science fact and science fiction. We are of course aware of an entire school of research on the foundations of quantum mechanics which may be labelled “Against Measurement”. However we think that there is more reality to measurement and dark energy than we initially thought [23]. For instance it is conceivable from the identity of the mathematical formalism of the quantum wave and that of quantum spacetime itself that these are different labels for what is essentially the same. Seen in this way the Feynmann propagator and the HawkingHartle wave are essentially a multi-fractal quantum spacetime. In such multi fractal real plethora of empty sets modelling spacetime, the speed of light is a variable ranging from zero to infinity while the constant C is only an average expectation value. Consequently our theory is essentially a fractal version of the theories of variable speed of light [23-26,34,35].
REFERENCES
- J. Nash, Annals of Mathematics, Vol. 63, 1956, p. 20. http://dx.doi.org/10.2307/1969989
- J. Nash, Koninklijke Nederlandse Akademie van Wetenschappen, Vol. 58, 1955, p. 545.
- M. S. El Naschie, Chaos, Solitons & Fractals, Vol. 18, 2003, pp. 635-641. http://dx.doi.org/10.1016/S0960-0779(03)00007-9
- R. Penrose, “The Road to Reality. A Complete Guide to the Laws of the Universe,” Jonathan Cape, London, 2004.
- W. Rindler, “Relativity,” Oxford Science Publications, Oxford, 2004.
- M. S. El Naschie and L. Marek-Crnjac, International Journal of Modern Nonlinear Theory and Application, Vol. 1, 2012, pp. 118-124. http://dx.doi.org/10.4236/ijmnta.2012.14018
- E. J. Copeland, M. Sami and S. Tsujikawa, “Dynamics of Dark Energy,” 2006. arXiv: hep-th/0603057
- L. Amendola and S. Tsujikawa, “Dark Energy: Theory and Observations,” Cambridge University Press, Cambridge, 2010. http://dx.doi.org/10.1017/CBO9780511750823
- M. S. El Naschie, Chaos, Solitons & Fractals, Vol. 41, 2009, p. 2635. http://dx.doi.org/10.1016/j.chaos.2008.09.059
- M. S. El Naschie, M. S. El Naschie, Chaos, Solitons & Fractals, Vol. 19, 2004, p. 209. http://dx.doi.org/10.1016/S0960-0779(03)00278-9
- M. S. El Naschie, Chaos, Solitons & Fractals, Vol. 30, 2006, p. 579. http://dx.doi.org/10.1016/j.chaos.2006.03.030
- J. Polchinski, “String Theory,” Cambridge University Press, Cambridge, 1998.
- M. S. El Naschie, International Journal of Nonlinear Sciences and Numerical Simulation, Vol. 7, 2006, p. 477.
- M. S. El Naschie, International Journal of Nonlinear Sciences and Numerical Simulation, Vol. 7, 2006, p. 407.
- M. S. El Naschie, L. Marek-Crnjac and J.-H. He, Fractal Spacetime & Noncommutative Geometry in Quantum & High Energy Physics, Vol. 2, 2012, p. 107.
- M. Duff, International Journal of Modern Physics A, Vol. 11, 1996, p. 5623. http://dx.doi.org/10.1142/S0217751X96002583
- L. Marek-Crnjac, J.-H. He and M. S. El Naschie, Fractal Spacetime & Noncommutative Geometry in Quantum & High Energy Physics, Vol. 2, 2012, p. 118.
- S. Nakajima, et al., “Foundations of Quantum Mechanics in The Light of New Technologies,” World Scientific, Singapore City, 1996.
- L. Marek-Crnjac, et al., International Journal of Modern Nonlinear Theory and Application, Vol. 2, 2013, p. 78.
- M.S. El Naschie, Journal of Quantum Information Science, Vol. 3, 2013, p. 23. http://dx.doi.org/10.4236/jqis.2013.31006
- L. Marek-Crnjac and J.-H. He, Fractal Spacetime and Noncommutative Geometry in Quantum and High Energy Physics, Vol. 2, 2012, p. 66.
- V Braginsky and S. P. Vyatchanin, Doklady Akademii Nauk SSSR, Vol. 259, 1981, p. 570. [Soviet Physics— Doklady, Vol. 27, 1982, p. 478].
- M. S. El Naschie, Journal of Modern Physics, Vol. 4, 2013, p. 591. http://dx.doi.org/10.4236/jmp.2013.45084
- M. S. El Naschie, International Journal of Modern Nonlinear Theory and Application, Vol. 2, 2013, p. 43. http://dx.doi.org/10.4236/ijmnta.2013.21005
- M.S. El Naschie, Journal of Quantum Information Science, Vol. 3, 2013, p. 57. http://dx.doi.org/10.4236/jqis.2013.32011
- P. S. Wesson, “Five Dimensional Physics,” World Scientific, Singapore City, 2006.
- M. S. El Naschie, “Stress, Stability and Chaos in Structural Engineering,” McGraw Hill, London, 1990.
- M. S. El Naschie, International Journal of Modern Nonlinear Theory and Application, Vol. 2, 2013, pp. 107-121. http://dx.doi.org/10.4236/ijmnta.2013.22014
- M. S. El Naschie, Chaos, Solitons & Fractals, Vol. 23, 2005, pp. 1511-1514. http://dx.doi.org/10.1016/j.chaos.2004.08.008
- M. S. El Naschie, Chaos, Solitons & Fractals, Vol. 23, 2005, pp. 1931-1933. http://dx.doi.org/10.1016/j.chaos.2004.08.004
- R. Calella, A. W. Overhauser and S. A. Werner, Physical Review Letters, Vol. 34, 1975, pp. 1472-1474. http://dx.doi.org/10.1103/PhysRevLett.34.1472
- V. V. Nesvizhevky and A. K. Petukhov, The European Physical Journal C, Vol. 40, 2005, pp. 479-491. http://dx.doi.org/10.1140/epjc/s2005-02135-y
- M. Reza Pahlavani, H. Rahbar and M. Ghezelbash, Open Journal of Microphysics, Vol. 3, 2013, pp. 1-7. http://dx.doi.org/10.4236/ojm.2013.31001
- J. Magueijo and J. W. Moffat, “Comments on ‘Note on Varying Speed of Light Theories’,” 2007. arXiv: 0705.4507
- J. Magueijo, “Faster Than the Speed of Light,” Arrow Books, The Random House, London, 2003.

