Journal of Modern Physics
Vol. 4 No. 8A (2013) , Article ID: 36087 , 11 pages DOI:10.4236/jmp.2013.48A006
Conservation of Gravitational Energy-Momentum and Inner Diffeomorphism Group Gauge Invariance
Aurorastr. 24, CH-8032, Zurich, Switzerland
Email: christian.wiesendanger@ubs.com
Copyright © 2013 Christian Wiesendanger. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received May 22, 2013; revised June 27, 2013; accepted July 31, 2013
Keywords: Gauge Field Theory; Volume-Preserving Diffeomorphism Group; Inner Minkowski Space
ABSTRACT
Viewing gravitational energy momentum 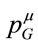 as equal by observation, but different in essence from inertial energy-momentum
as equal by observation, but different in essence from inertial energy-momentum 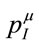 requires two different symmetries to account for their independent conservations—spacetime and inner translation invariance. Gauging the latter a generalization of non-Abelian gauge theories of compact Lie groups is developed resulting in the gauge theory of the non-compact group of volume-preserving diffeomorphisms of an inner Minkowski space M4. As usual the gauging requires the introduction of a covariant derivative, a gauge field and a field strength operator. An invariant and minimal gauge field Lagrangian is derived. The classical field dynamics and the conservation laws for the new gauge theory are developed. Finally, the theory’s Hamiltonian in the axial gauge is expressed by two times six unconstrained independent canonical variables obeying the usual Poisson brackets and the positivity of the Hamiltonian is related to a condition on the support of the gauge fields.
requires two different symmetries to account for their independent conservations—spacetime and inner translation invariance. Gauging the latter a generalization of non-Abelian gauge theories of compact Lie groups is developed resulting in the gauge theory of the non-compact group of volume-preserving diffeomorphisms of an inner Minkowski space M4. As usual the gauging requires the introduction of a covariant derivative, a gauge field and a field strength operator. An invariant and minimal gauge field Lagrangian is derived. The classical field dynamics and the conservation laws for the new gauge theory are developed. Finally, the theory’s Hamiltonian in the axial gauge is expressed by two times six unconstrained independent canonical variables obeying the usual Poisson brackets and the positivity of the Hamiltonian is related to a condition on the support of the gauge fields.
1. Introduction
Field theory provides a powerful way to represent fundamental conservation laws of Nature in a mathematically consistent framework through Noether’s theorem which relates any global invariance of the underlying field theory under a continous symmetry group to a number of conserved currents and charges. Conservation of electric charge and 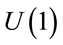 -invariance, conservation of Color and
-invariance, conservation of Color and  -invariance or conservation of inertial energy-momentum and translation invariance in spacetime are but three key examples.
-invariance or conservation of inertial energy-momentum and translation invariance in spacetime are but three key examples.
Moreover, through the gauge principle the field theory framework allows to construct new fields together with their dynamics and through minimal coupling it allows to fix the coupling to other fields obeying a given global symmetry in a way which extends it to a local invariance of the thus completed field theory [1]. The new fields transmit the physical interactions between the various minimally coupled fields (and between themselves in all cases with a non-Abelian underlying symmetry). The dynamics of the Standard Model (SM) has been modelled along this way starting with Electrodynamics, extending it to electro-weak interactions and finally adding Chromodynamics which models the strong interaction [2,3].
And General Relativity (GR) can be constructed along this way as well [4].
There is, however, a crucial difference between the SM and GR when attempting to quantize the respective classical gauge field theories. The quantized SM is a perfectly consistent quantum field theory (QFT) related to its renormalizability—at least at the perturbation theory level. Any attempt to consistently quantize GR or extensions thereof have failed so far already at the perturbation theory level due to the intrinsic non-renormalizability of the theory [5,6].
Whereas in the SM spacetime and its Minkowskian geometry are an A Priori which serves as the arena within which the dynamics of the various matter and gauge fields unfolds GR declares spacetime itself a dynamical element whose geometry evolves alongside the changing energy-momentum distribution of the matter and gauge fields present. Not only does this dynamization of spacetime render GR non-renormalizable, but it also destroys basic concepts such as the energy-momentum density of the gravitational field or the relation between a quantized field and its corresponding particle which both rely on global translation invariance in spacetime and are crucial for the physical interpretation of a QFT [5,6].
To map out an alternative route to a viable field theory of gravitation let us go back to the very fundament— namely the two experimental observations that (1) the inertial and gravitational masses of a physical body are numerically equal, 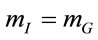 , and (2) the inertial energymomentum of a closed physical system is conserved,
, and (2) the inertial energymomentum of a closed physical system is conserved,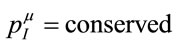 . Taking both together we then can write in the rest frame of the body
. Taking both together we then can write in the rest frame of the body
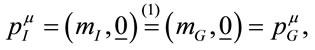 (1)
(1)
where we have tentatively introduced the gravitational energy-momentum 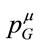 which we keep as an entity a priorily different from
which we keep as an entity a priorily different from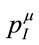 . Note that
. Note that 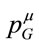 is conserved due to Equation (1).
is conserved due to Equation (1).
In GR 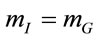 is interpreted as an essential identity which leads to the aforementioned geometrical description of gravitation.
is interpreted as an essential identity which leads to the aforementioned geometrical description of gravitation.
In this paper we propose to follow a different route and investigate the consequences of viewing 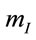 and
and 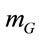 or
or 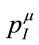 and
and 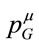 as different by their very natures— the prevailing view before Einstein which comes at the price of accepting the observed numerical equality
as different by their very natures— the prevailing view before Einstein which comes at the price of accepting the observed numerical equality 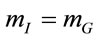 as accidential.
as accidential.
Both 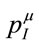 and
and 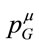 are four-vectors then which are conserved, but through two different mechanisms. Obviously the conservation of
are four-vectors then which are conserved, but through two different mechanisms. Obviously the conservation of 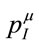 is related to translation invariance in spacetime. Let us use Noether’s theorem to separately derive the conservation of a new four-vector in a field theoretical framework relating it to a continous symmetry of the theory which we will call inner translation invariance. That four-vector is then interpreted as the gravitational energy-momentum
is related to translation invariance in spacetime. Let us use Noether’s theorem to separately derive the conservation of a new four-vector in a field theoretical framework relating it to a continous symmetry of the theory which we will call inner translation invariance. That four-vector is then interpreted as the gravitational energy-momentum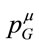 .
.
This will be the first step in developing an alternative route to describe gravity. The second will be to gauge the inner translation group and to develop the gauge field theory of inner diffeomorphisms technically leveraging earlier work on generalizing Yang-Mills theories to gauge groups with infinitely many degrees of freedom [7, 8]. The resulting Lagrangian and Hamiltonian dynamics are the basis to interpret the theory as a theory of gravitation [9] and to show its renormalizability at the QFT level [10] in two forthcoming papers.
The notations and conventions used follow closely to those of Steven Weinberg in his classic account on the quantum theory of fields [2,3]. They are presented in the Appendix.
2. Global Diffeomorphism Invariance and Conservation of Gravitational Energy-Momentum
In this section, we introduce the concept of global diffeomorphism invariance in inner space for a generic field theory in order to generate a new conserved four-vector through Noether’s theorem which will serve as gravitational energy-momentum.
Let us start with a four-dimensional real vector space 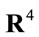 with elements labelled
with elements labelled 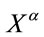 without a metric structure at this point which we will call inner space in the following. Volume-preserving diffeomorphisms
without a metric structure at this point which we will call inner space in the following. Volume-preserving diffeomorphisms
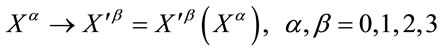 (2)
(2)
act as a group  under composition on this space.
under composition on this space. 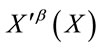 denotes an invertible and differentiable coordinate transformation of
denotes an invertible and differentiable coordinate transformation of 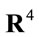 with unimodular Jacobian
with unimodular Jacobian
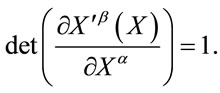 (3)
(3)
The restriction to volume-preserving transformations will automatically ensure global gauge invariance of the theories we look at in the sequel and will prove crucial for the consistency of our approach.
To represent this group in field space we have to add additional degrees of freedom in complete analogy to the Yang-Mills case where fields become vectors on which representations of a finite-dimensional symmetry group act.
Hence we consider fields 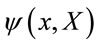 defined on the product of the four-dimensional Minkowski spacetime
defined on the product of the four-dimensional Minkowski spacetime 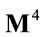 and the four-dimensional inner space
and the four-dimensional inner space 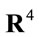 introduced above. The fields
introduced above. The fields 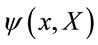 are assumed to be infinitely differentiable in both
are assumed to be infinitely differentiable in both 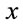 and X and to vanish at infinity. They form a linear space endowed with the scalar product
and X and to vanish at infinity. They form a linear space endowed with the scalar product
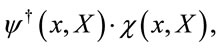
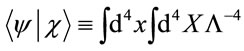 (4)
(4)
where we introduce a parameter  of dimension length,
of dimension length,  , so as to define a dimensionless scalar product.
, so as to define a dimensionless scalar product.  will play an important role in the definition of the gauge field action later.
will play an important role in the definition of the gauge field action later.
Note that the fields 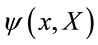 might live in non-trivial representation spaces of both the Lorentz group with spin
might live in non-trivial representation spaces of both the Lorentz group with spin 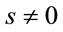 and of other inner symmetry groups such as
and of other inner symmetry groups such as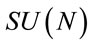 . All these scalar, spinor and gauge vector fields —apart from the gauge field related to diffeomorphism invariance to be introduced below—are called “matter” fields in the following. These representations factorize w.r.t the diffeomorphism group representations we introduce below which is consistent with the Coleman-Mandula theorem.
. All these scalar, spinor and gauge vector fields —apart from the gauge field related to diffeomorphism invariance to be introduced below—are called “matter” fields in the following. These representations factorize w.r.t the diffeomorphism group representations we introduce below which is consistent with the Coleman-Mandula theorem.
Let us assume in the sequel that the dynamics of the field 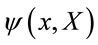 is specified by a Lagrangian of the form
is specified by a Lagrangian of the form
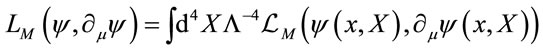 (5)
(5)
with a real Lagrangian density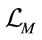 . The integration measure in inner space comes along with a factor of
. The integration measure in inner space comes along with a factor of 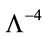 to keep inner integrals dimensionless. The subscript
to keep inner integrals dimensionless. The subscript 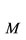 denotes generic fermionic and bosonic matter in this context.
denotes generic fermionic and bosonic matter in this context.
Turning to the transformation behaviour of the Lagrangian Equation (5) under infinitesimal diffeomorphism transformations we start with the passive representation of 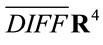 in field space for infinitesimal transformations
in field space for infinitesimal transformations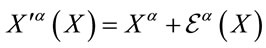
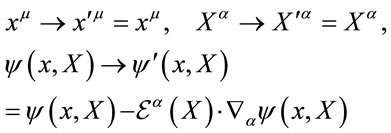 (6)
(6)
transforming the fields only.
The unimodularity condition Equation (3) translates into the infinitesimal gauge parameter 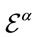 being divergence-free
being divergence-free
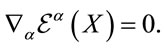 (7)
(7)
Note the crucial fact that the algebra  of the divergence-free
of the divergence-free 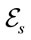 closes under commutation. For
closes under commutation. For 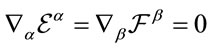 we have
we have
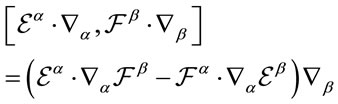 (8)
(8)
with
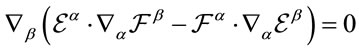 (9)
(9)
as required by the finite transformations  forming a group under composition.
forming a group under composition.
As a result we can write infinitesimal transformations in field space
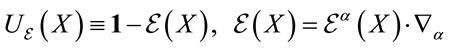 (10)
(10)
as anti-unitary operators w.r.t. the scalar product Equation (4). Both the 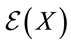 and the
and the 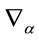 are anti-hermitean w.r.t. the scalar product Equation (4).
are anti-hermitean w.r.t. the scalar product Equation (4).
The decomposability of 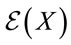 w.r.t. to the operators
w.r.t. to the operators 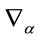 will be crucial for the further development of the theory, especially for identifying the gauge field variables of the theory.
will be crucial for the further development of the theory, especially for identifying the gauge field variables of the theory.
Introducing the variation 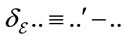 of an expression under a gauge transformation we can write
of an expression under a gauge transformation we can write
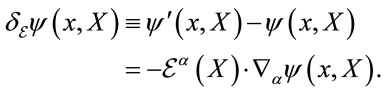 (11)
(11)
The variation of the Lagrangian density 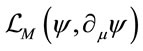 —depending on
—depending on  and
and  only through the fields
only through the fields 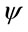 and their
and their 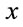 -derivatives
-derivatives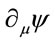 —becomes
—becomes
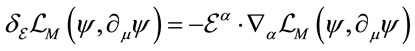 (12)
(12)
implying the global invariance of the corresponding Lagrangian
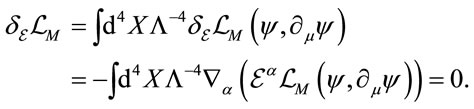 (13)
(13)
Here we have used the unimodularity condition 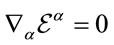 so that the
so that the  -integration yields zero for fields
-integration yields zero for fields  and gauge parameters
and gauge parameters  vanishing at infinity in X-space. As a result any matter Lagrangian is automatically globally gauge invariant under volume-preserving diffeomorphisms.
vanishing at infinity in X-space. As a result any matter Lagrangian is automatically globally gauge invariant under volume-preserving diffeomorphisms.
The invariance Equation (13) implies the existence of four conserved Noether currents
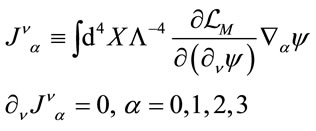 (14)
(14)
and the four time-independent charges
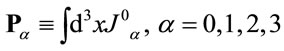 (15)
(15)
which generate the inner global coordinate transformations in field space. It is these currents and charges which will be interpreted in terms of gravitational energy-momentum and become the sources of  gauge fields.
gauge fields.
3. Local Diffeomorphism Invariance, Covariant Derivatives and Gauge Fields
In this section we introduce local gauge transformations and—to make globally invariant Lagrangians locally invariant—the corresponding covariant derivatives, gauge field and covariant field strength operators. We also define global inner scale transformations under which the covariant derivative, gauge field and covariant field strength operators are invariant.
Let us extend the global volume-preserving diffeomorphism group represented in field space to a group of local transformations by allowing 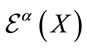 to vary with
to vary with 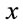 as well, i.e. allowing for
as well, i.e. allowing for 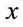 -dependent volume-preserving general coordinate transformations
-dependent volume-preserving general coordinate transformations 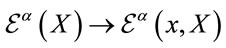 in inner space. In other words the group we gauge is the group of all isometric diffeomorphisms preserving the volume in inner space.
in inner space. In other words the group we gauge is the group of all isometric diffeomorphisms preserving the volume in inner space.
In generalization of Equation (9) we thus consider
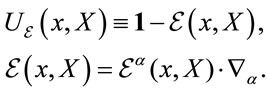 (16)
(16)
The formulae Equations (6) together with Equation (7) still define the representation of the volume-preserving diffeomorphism group in field space.
To assure local gauge covariance for globally diffeomorphism covariant Lagrangian densities as in Equation (11) we must introduce a covariant derivative 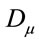 which is defined by the transformation requirement
which is defined by the transformation requirement
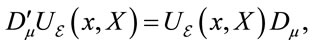 (17)
(17)
where 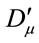 denotes the gauge-transformed covariant derivative.
denotes the gauge-transformed covariant derivative.
By construction the Lagrangian density in Equation (5) with covariant derivatives replacing the ordinary ones 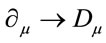 transforms covariantly under local infinitesimal transformations
transforms covariantly under local infinitesimal transformations
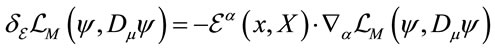 (18)
(18)
and the corresponding Lagrangian is locally gauge invariant
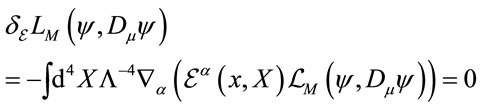 (19)
(19)
again due to the unimodularity condition 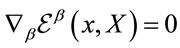 .
.
Next, to fulfil Equation (16) we make the usual ansatz
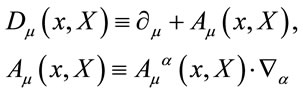 (20)
(20)
decomposing 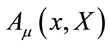 w.r.t the generators
w.r.t the generators 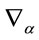 of the diffeomorphism algebra in field space. In order to have the gauge fields in the algebra
of the diffeomorphism algebra in field space. In order to have the gauge fields in the algebra  we impose in addition
we impose in addition
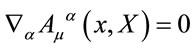 (21)
(21)
consistent with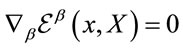 . As a consequence the usual ordering problem for
. As a consequence the usual ordering problem for 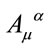 and
and 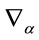 in the definition of
in the definition of 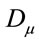 does not arise and
does not arise and 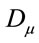 is anti-hermitean w.r.t to the scalar product defined above.
is anti-hermitean w.r.t to the scalar product defined above.
The requirement Equation (16) translates into the transformation law for the gauge field
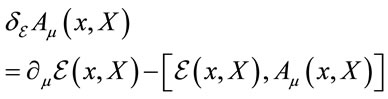 (22)
(22)
which reads in components
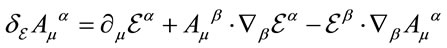 (23)
(23)
respecting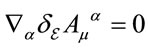 . The inhomogenous term
. The inhomogenous term 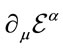 assures the desired transformation behaviour of the
assures the desired transformation behaviour of the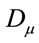 , the term
, the term 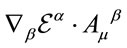 rotates the inner space vector
rotates the inner space vector 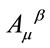 and the term
and the term 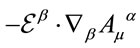 shifts the coordinates
shifts the coordinates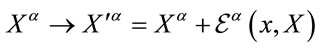 .
.
Note that the consistent decomposition of both 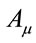 and
and 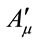 w.r.t. the generators
w.r.t. the generators 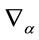 is crucial for the theory’s viability. It is ensured by the closure of the algebra Equation (7) and the gauge invariance of
is crucial for the theory’s viability. It is ensured by the closure of the algebra Equation (7) and the gauge invariance of 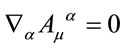 for gauge parameters fulfilling
for gauge parameters fulfilling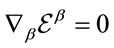 .
.
Let us next define the field strength operator 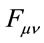 in the usual way
in the usual way
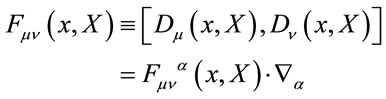 (24)
(24)
which again can be decomposed consistently w.r.t.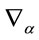 . The field strength components
. The field strength components 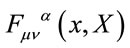 are calculated to be
are calculated to be
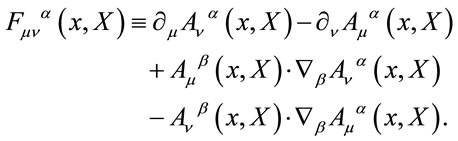 (25)
(25)
Under a local gauge transformation the field strength and its components transform covariantly
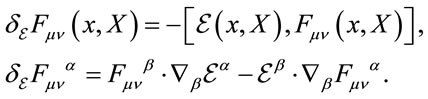 (26)
(26)
As required for algebra elements 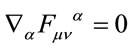 and
and 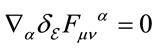 for gauge fields fulfilling
for gauge fields fulfilling 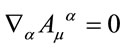 and gauge parameters fulfilling
and gauge parameters fulfilling .
.
Besides the global and local invariance under inner coordinate transformations Equations (6) the theory features another global invariance in inner space—namely scale invariance. Let us give the respective transformation law for a rescaling with scale parameter 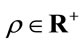
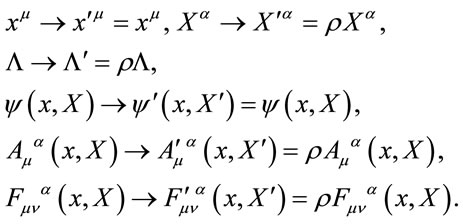 (27)
(27)
Under Equation (27) matter Lagrangians and the operators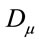 ,
, 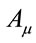 and
and 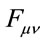 are invariant which will prove crucial to consistently define the theory below.
are invariant which will prove crucial to consistently define the theory below.
4. The Lagrangian
In this section we introduce a metric in the inner space and derive the gauge field Lagrangian minimal in the sense of being gauge-invariant and of lowest possible dimension in the fields.
As heuristically motivated by analogy to the YangMills case we propose the local gauge field Lagrangian to be proportional to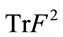 —ensuring gauge invariance and at most second order dependence on the first derivatives of the
—ensuring gauge invariance and at most second order dependence on the first derivatives of the 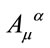 -fields which is crucial for a quantization leading to a unitary and renormalizable theory.
-fields which is crucial for a quantization leading to a unitary and renormalizable theory.
To make sense of the formal operation 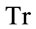 and to define
and to define 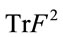 properly let us start with the evaluation of the differential operator product
properly let us start with the evaluation of the differential operator product
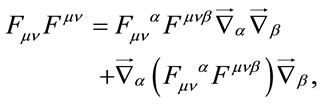 (28)
(28)
where 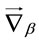 acts on all fields to its right.
acts on all fields to its right.
To be able to evaluate the trace in a coordinate system we would like to insert complete systems of 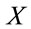 - and
- and 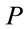 -vectors
-vectors
 (29)
(29)
under the 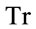 -operation and using
-operation and using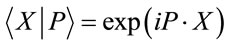 . This assumes, however, the existence of Cartesian coordinates and a metric in inner space and the existence of both coand contravariant vectors w.r.t. that metric.
. This assumes, however, the existence of Cartesian coordinates and a metric in inner space and the existence of both coand contravariant vectors w.r.t. that metric.
So let us endow the inner four-dimensional real vector space 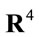 with a metric
with a metric 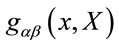 of Minkowskian signature and require that its geometry—which we take as an a priori—is flat,
of Minkowskian signature and require that its geometry—which we take as an a priori—is flat,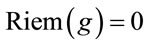 . This means that it is always possible to choose global Cartesian coordinates with the metric
. This means that it is always possible to choose global Cartesian coordinates with the metric 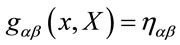 collapsing to the global Minkowski metric. Such choices of coordinates amount to partially fixing a gauge and we will call them Minkowskian gauges in the following.
collapsing to the global Minkowski metric. Such choices of coordinates amount to partially fixing a gauge and we will call them Minkowskian gauges in the following.
Note that under inner coordinate transformations the metric transforms as a contravariant tensor
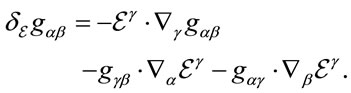 (30)
(30)
Working in Cartesian coordinates we can now insert complete systems of 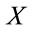 - and
- and 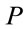 -vectors and formally take the trace over the inner space
-vectors and formally take the trace over the inner space
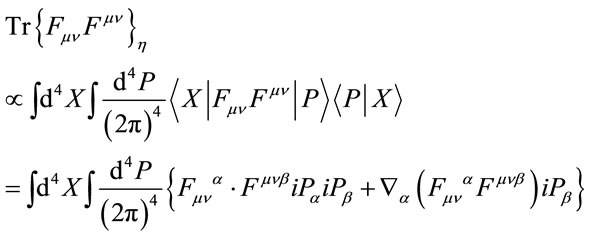 (31)
(31)
which has still to be properly defined. Above we have made use of 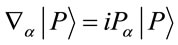 and the subscript
and the subscript 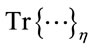 denotes evaluation in a given coordinate system and for a given metric, in this case Cartesian coordinates and the Minkowski metric. Note that beeing a total divergence in
denotes evaluation in a given coordinate system and for a given metric, in this case Cartesian coordinates and the Minkowski metric. Note that beeing a total divergence in  -space and odd in
-space and odd in  the second term in Equation (31) vanishes.
the second term in Equation (31) vanishes.
The definition of the remaining P-integral requires care in order to covariantly deal with the infinities resulting from the non-compactness of the gauge group. Noting that the regularization will restrict 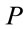 to the forward and backward light cones, i.e.
to the forward and backward light cones, i.e. 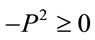 we extract the tensor structure
we extract the tensor structure
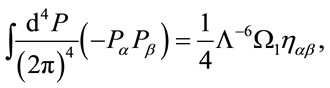 (32)
(32)
and isolate the infinity into a dimensionless Lorentzinvariant integral of the type
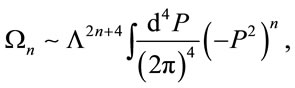 (33)
(33)
where the subscript counts powers of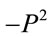 . Slicing the inner Minkowski space into light-like, time-like and spacelike shells of invariant lengths
. Slicing the inner Minkowski space into light-like, time-like and spacelike shells of invariant lengths 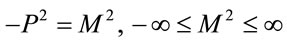 which are invariant under proper Lorentz transformations we can identically rewrite
which are invariant under proper Lorentz transformations we can identically rewrite
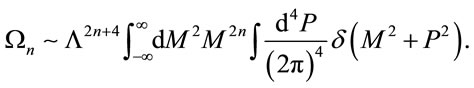 (34)
(34)
To regularize 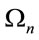 in a Lorentz-invariant way we first cut off the space-like shells with negative lengths
in a Lorentz-invariant way we first cut off the space-like shells with negative lengths 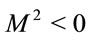 and split
and split 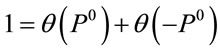 so that
so that
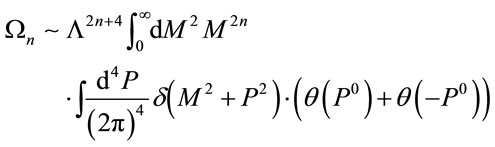 (35)
(35)
which is a Lorentz-invariant procedure. As we will see in the section on Hamiltonian field dynamics this cutoff arises naturally from the condition of positivity for the Hamiltonian which will restrict all fields Fourier-transformed over inner space to have support on the set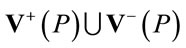 , where
, where
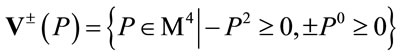 (36)
(36)
denote the forward and backward light cones.
Second, there is always a Lorentz frame with a timelike vector 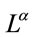 which has
which has 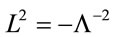 as its invariant length so that
as its invariant length so that 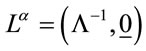 in this frame. Third,
in this frame. Third,
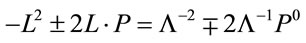 (37)
(37)
are Lorentz scalars.
This allows us to define 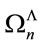 as an integral over of the forward cone
as an integral over of the forward cone 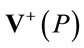 with a cutoff for
with a cutoff for
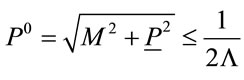 and the backward cone
and the backward cone 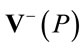 with a cutoff for
with a cutoff for 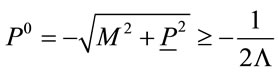 for fixed
for fixed 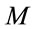 first and then summing over all
first and then summing over all 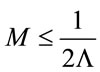
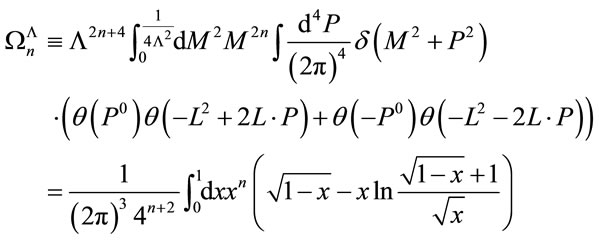 (38)
(38)
which is a positive and finite Lorentz scalar for all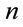 .
.
Explicitly we find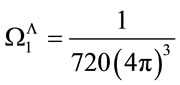 . As
. As 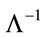 is the only a priori mass scale in the theory any other Lorentzinvariant regularization procedure just changes the numerical values of
is the only a priori mass scale in the theory any other Lorentzinvariant regularization procedure just changes the numerical values of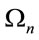 .
.
Note that regularized in this way any inner 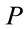 -integral over polynomials in P reduces to products of the metric in inner space and
-integral over polynomials in P reduces to products of the metric in inner space and 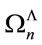 and is as well behaved as the usual sums over structure constants of a compact Lie group are in a Yang-Mills theory.
and is as well behaved as the usual sums over structure constants of a compact Lie group are in a Yang-Mills theory.
Using Equations (32) and (38) to evaluate Equation (31) we now define a 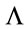 -dependent trace in Minkowskian gauges by
-dependent trace in Minkowskian gauges by
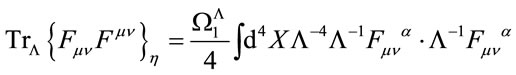 (39)
(39)
which is easily generalized to arbitrary coordinates in inner space
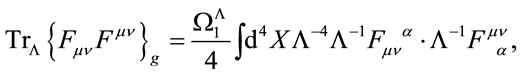 (40)
(40)
where we have to contract the inner indices with 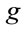 now. The expression above is obviously well defined in any coordinate system and gauge-invariant under the combined transformations of field strength components Equations (26) and the metric Equation (30).
now. The expression above is obviously well defined in any coordinate system and gauge-invariant under the combined transformations of field strength components Equations (26) and the metric Equation (30).
Finally this allows us to write down the Lagrangian for the gauge fields
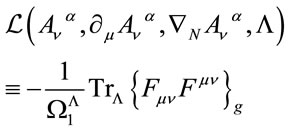 (41)
(41)
and the corresponding Lagrangian density
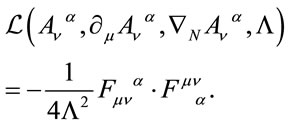 (42)
(42)
Both are dimensionless in inner space—the Lagrangian density due to the factors of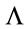 . Note that the factor of
. Note that the factor of 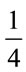 above leads to the usual normalization of the quadratic part of the Lagrangian density and the overall minus sign will yield a positive Hamiltonian as we will show in the section on Hamiltonian field dynamics.
above leads to the usual normalization of the quadratic part of the Lagrangian density and the overall minus sign will yield a positive Hamiltonian as we will show in the section on Hamiltonian field dynamics.
Note that the Lagrangian for 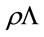 is related to the Lagrangian for a given
is related to the Lagrangian for a given 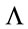 by
by
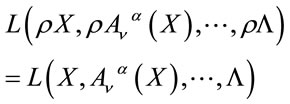 (43)
(43)
with a similar relation holding for the matter Lagrangian Equation (5)—the dependence of the theory on 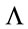 is controlled by the scale transformation Equation (27). In other words theories for different
is controlled by the scale transformation Equation (27). In other words theories for different 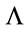 are equivalent up to inner rescalings.
are equivalent up to inner rescalings.
This is a crucial point which will allow us to rescale 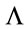 always to the Planck length, a fact we will use when extracting the physics of the theory at hands.
always to the Planck length, a fact we will use when extracting the physics of the theory at hands.
Why have we not simply written down Equation (41)? First, the calculation starting with the 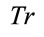 -operation shows that the dimensionful parameter
-operation shows that the dimensionful parameter 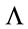 automatically emerges in the definition of the Lagrangian and that the theory at
automatically emerges in the definition of the Lagrangian and that the theory at 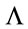 is related in a simple way to the one at
is related in a simple way to the one at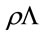 . We would not have uncovered this somewhat hidden, but crucial fact in simply writing down the Lagrangian. Second, we will have to show in the quantized version of the theory that the kinematic integrals generalizing the kinematic sums over gauge degrees of freedom in the Yang-Mills case can be consistently defined. The definition of
. We would not have uncovered this somewhat hidden, but crucial fact in simply writing down the Lagrangian. Second, we will have to show in the quantized version of the theory that the kinematic integrals generalizing the kinematic sums over gauge degrees of freedom in the Yang-Mills case can be consistently defined. The definition of 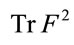 is a first example of how this will be achieved.
is a first example of how this will be achieved.
5. Lagrangian Field Dynamics
In this section we develop the Lagrangian field dynamics determining the field equations which will not depend on the metric g and derive the most important conservation laws for the theory.
Note that by definition we always work with fields living in the algebra 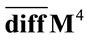 from now on. We start with the action
from now on. We start with the action
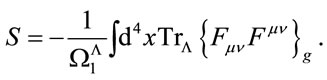 (44)
(44)
Variation of Equation (44) w.r.t. 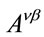 to get a stationary point
to get a stationary point
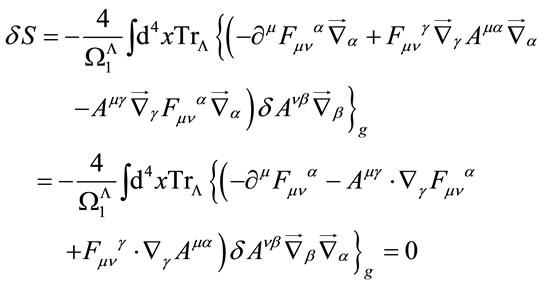 (45)
(45)
yields the field equations
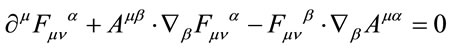 (46)
(46)
which by inspection do not depend on the metric. This means that the metric g is not an independent dynamical field and irrelevant for the dynamics of the gauge fields. Above we have used the cyclicality of the trace, partially integrated and brought all the  to the right. Note that under the trace all terms with an odd number of
to the right. Note that under the trace all terms with an odd number of 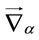 vanish.
vanish.
The equations of motion can be brought into a covariant form
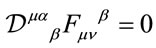 (47)
(47)
introducing the covariant derivative 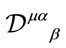 acting on vectors in inner space
acting on vectors in inner space
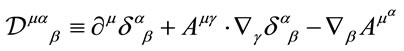 (48)
(48)
By inspection the covariant derivative Equation (48) respects the gauge algebra and is an endomorphism of  because
because
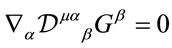 (49)
(49)
for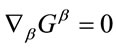 .
.
Finally we can recast the field equations in coordinateindependent and manifestly covariant form
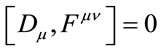 (50)
(50)
underlining the formal similarity of the present theory to Yang-Mills theories of compact Lie groups.
The  field equations Equations (46) clearly display the self coupling of the
field equations Equations (46) clearly display the self coupling of the 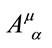 -fields to the four conserved Noether current densities
-fields to the four conserved Noether current densities
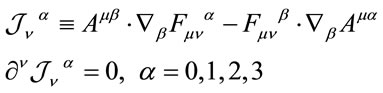 (51)
(51)
which obey the restrictions on algebra elements 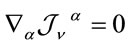 as expected.
as expected.
Next we analyze the invariance of the action Equation (44) under spacetime translations and derive the conserved energy-momentum tensor. In the usual way we obtain the canonical energy-momentum tensor
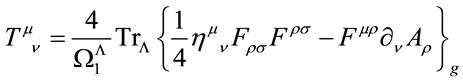 (52)
(52)
which is conserved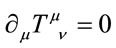 . As in other gauge field theories this tensor is, however, not gauge invariant. Using the field equations Equations (50) and the cyclicality of the trace we find
. As in other gauge field theories this tensor is, however, not gauge invariant. Using the field equations Equations (50) and the cyclicality of the trace we find
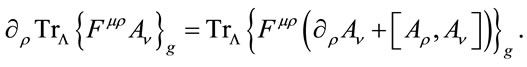 (53)
(53)
Adding this total divergence we finally get an improved, conserved and gauge-invariant energy-momentum tensor
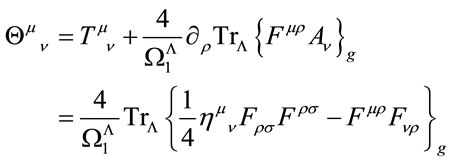 (54)
(54)
which reads in components
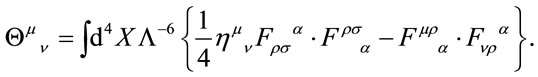 (55)
(55)
The corresponding time-independent momentum fourvector reads
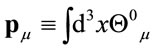 (56)
(56)
and generates the translations in spacetime.
In addition, the theory is obviously Lorentz and—at the classical level—scale invariant under the corresponding spacetime and field transformations. We do not display the corresponding conserved currents and charges here.
Let us finally write down the Bianchi identities
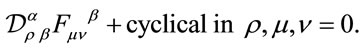 (57)
(57)
The equations above define a perfectly consistent classical dynamical system within the Lagrangian framework. Note that for physical observables such as the energy-momentum tensor the inner degrees of freedom are integrated over.
As we ultimately aim at quantizing the theory we next turn to develop the Hamiltonian field theory.
6. Hamiltonian Field Dynamics
In this section we develop the Hamiltonian field dynamics closely following [3]. We fix a gauge first choosing Cartesian coordinates along with the Minkowski metric in inner space and second eliminating the first class constraints related to the remaining gauge degrees of freedom by imposing the axial gauge condition. We then explicitely solve the remaining constraints and find the unconstrained canonical variables for the theory. Finally we re-express the gauge-fixed Hamiltonian H of the theory in these variables displaying its positivity explicitly. This will serve in [10] as the starting point for quantization.
Let us start using the gauge freedom of the theory to choose Cartesian coordinates along with the Minkowski metric in inner space, i.e. fixing a gauge up to coordinate transformations Equations (16) which leave the Minkowski metric invariant. The remaining gauge group is just the Poincaré group acting on the inner Minkowski space with infinitesimal parameters
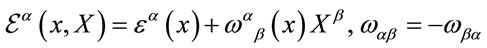 .
.
Hence, we start with the Lagrangian density Equation (42)
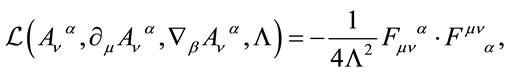 (58)
(58)
where the 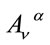 are the gauge fields,
are the gauge fields, 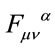 are given by Equation (25) and where the
are given by Equation (25) and where the 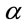 -indices are raised and lowered with
-indices are raised and lowered with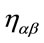 .
.
Next we define the variables 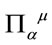 conjugate to
conjugate to 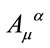 by
by
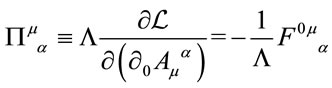 (59)
(59)
which are dimensionless in inner space. By definition they are elements of the gauge algebra  and fulfil
and fulfil
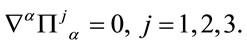 (60)
(60)
As usual we find the two sets of four constraints
 (61)
(61)
and
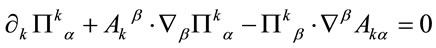 (62)
(62)
which are the field equations Equation (46) for 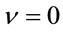 and
and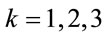 .
.
The Poisson brackets of the two constraints Equations (61) and (62) w.r.t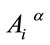 ,
, 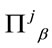 vanish because Equation (62) is independent of
vanish because Equation (62) is independent of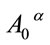 . Hence, they are first class. To properly deal with them we fully fix the remaining gauge degrees of freedom—Poincaré transformations which leave the Minkowski metric invariant—by imposing the axial gauge condition
. Hence, they are first class. To properly deal with them we fully fix the remaining gauge degrees of freedom—Poincaré transformations which leave the Minkowski metric invariant—by imposing the axial gauge condition
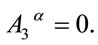 (63)
(63)
The canonical variables of the theory reduce to 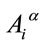 and their conjugates
and their conjugates 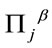
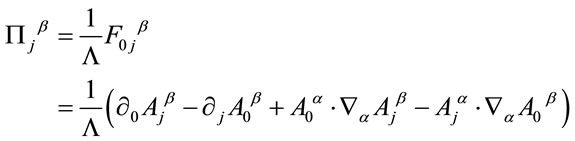 (64)
(64)
for 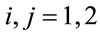 only.
only.
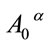 is not an independent variable, but can be expressed in terms of the canonical variables above by solving the constraint Equation (62)
is not an independent variable, but can be expressed in terms of the canonical variables above by solving the constraint Equation (62)
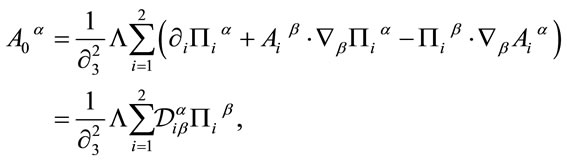 (65)
(65)
where we have used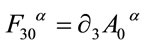 .
.
Finally we solve the unimodularity constraints on 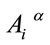
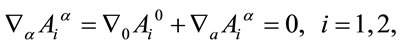 (66)
(66)
where 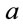 runs over
runs over 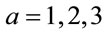 to obtain
to obtain
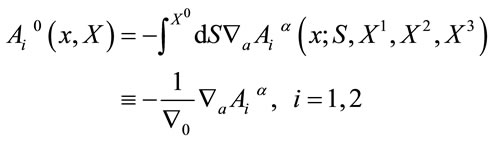 (67)
(67)
and analogously for 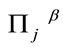
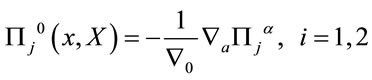 (68)
(68)
further reducing the independent variables to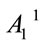 ,
, 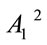 ,
, 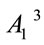 ,
, 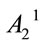 ,
, 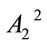 ,
, 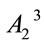 and the respective
and the respective 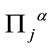 s.
s.
The Hamiltonian in the original gauge field variables
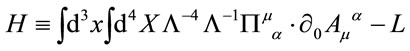 (69)
(69)
reduces in the axial gauge to
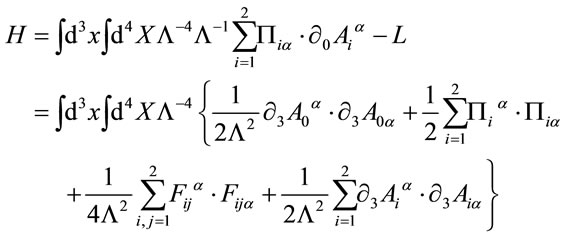 (70)
(70)
where we have made use of Equations (62) and (64) to rearrange terms and where 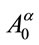 is given by Equation (65). Note that
is given by Equation (65). Note that 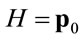 as expected.
as expected.
The use of Equation (67) allows us next to rewrite
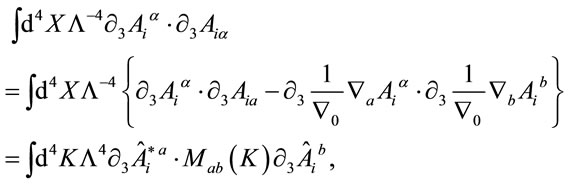 (71)
(71)
where we have Fourier-transformed 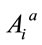 in inner space
in inner space
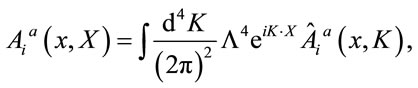 (72)
(72)
used the reality condition on 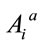
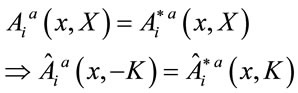 (73)
(73)
and introduced the matrix
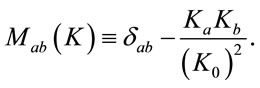 (74)
(74)
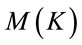 is real, symmetric with eigenvalues
is real, symmetric with eigenvalues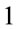 ,
, 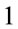 and
and
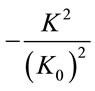 . Hence, there exists an orthogonal
. Hence, there exists an orthogonal 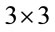 -matrix
-matrix
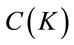 ,
, 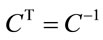 which diagonalizes
which diagonalizes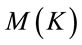 :
:
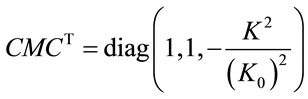 . Rotating
. Rotating
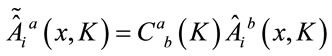 (75)
(75)
and using analogous expressions for all the terms appearing in Equation (70) we finally get 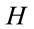 in terms of the unconstrained independent variables
in terms of the unconstrained independent variables ,
,  ,
, 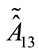 ,
, 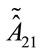 ,
, 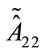 ,
, 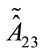 and the respective
and the respective 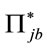 s
s
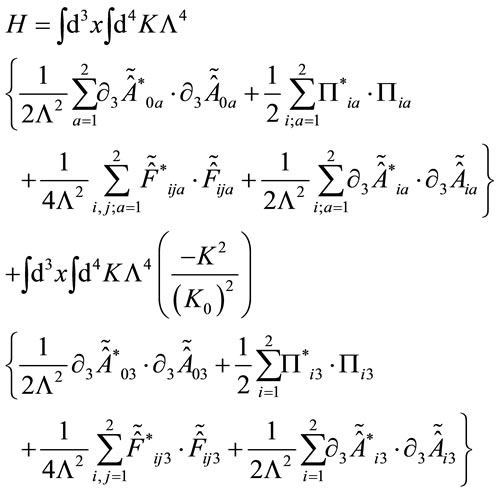 (76)
(76)
We immediately recognize that positivity of 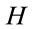 is ensured by the independent field variables of the theory vanishing outside the set
is ensured by the independent field variables of the theory vanishing outside the set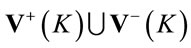 , i.e.
, i.e.
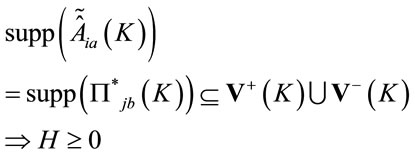 (77)
(77)
which is obviously a Lorentz-invariant requirement. Hence we restrict all fields in inner 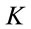 -space to have positive mass-squared support in
-space to have positive mass-squared support in 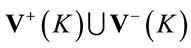 which defines in turn the class of admissible functional spaces for the fields of the theory. Note that the Fourier-transformed fields constant in
which defines in turn the class of admissible functional spaces for the fields of the theory. Note that the Fourier-transformed fields constant in  -space have support
-space have support 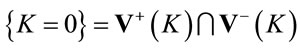 and hence positive
and hence positive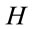 .
.
To specify the dynamics we finally write down the equal-time Poisson brackets for the unconstrained independent field variables 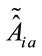 and
and 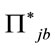 with positive mass-squared support
with positive mass-squared support
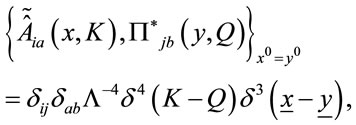 (78)
(78)
where 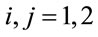 and
and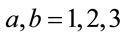 . The time evolution of observables in the theory is then given by the Poisson bracket of the Hamiltonian with a local observable
. The time evolution of observables in the theory is then given by the Poisson bracket of the Hamiltonian with a local observable 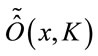 expressed in terms of the unconstrained independent field variables
expressed in terms of the unconstrained independent field variables 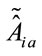 and
and 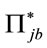 with positive mass-squared support
with positive mass-squared support
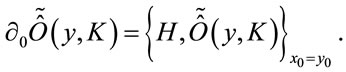 (79)
(79)
The time evolution is compatible with the support condition Equation (71). Together, Equations (76) and (79) constitute a perfectly consistent classical Hamiltonian field theory for the 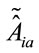 -fields and their conjugates
-fields and their conjugates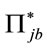 .
.
Note finally that both transformations (1) the inverse of Equation (75) rotating the fields with orthogonal matrices in field space and (2) the inverse Fourier transformation back to 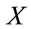 -space of fields with positive mass-squared support in
-space of fields with positive mass-squared support in 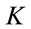 -space are canonical, hence allowing us equally well to start with the Hamiltonian given by Equation (70) where
-space are canonical, hence allowing us equally well to start with the Hamiltonian given by Equation (70) where 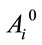 and
and 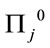 are expressed in terms of the independent variables
are expressed in terms of the independent variables 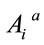 and
and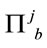 . The positivity of the Hamiltonian is again assured by the restriction to fields whose Fourier-transformed live in the functional spaces of fields with positive masssquared support in
. The positivity of the Hamiltonian is again assured by the restriction to fields whose Fourier-transformed live in the functional spaces of fields with positive masssquared support in 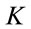 -space, a fact which is hidden working in the original
-space, a fact which is hidden working in the original 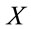 -variables. The Poisson brackets though get replaced by the appropriate Dirac brackets [2].
-variables. The Poisson brackets though get replaced by the appropriate Dirac brackets [2].
7. Inclusion of Matter Fields
Let us finally comment on the inclusion of matter fields. The minimal coupling prescription suggests to couple matter by (1) allowing fields to live on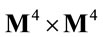 — adding the necessary additional inner degrees of freedom —and by (2) replacing ordinary derivatives through covariant ones
— adding the necessary additional inner degrees of freedom —and by (2) replacing ordinary derivatives through covariant ones 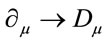 in matter Lagrangians as usual. As this prescription involves scalars in inner space only and as the volume element
in matter Lagrangians as usual. As this prescription involves scalars in inner space only and as the volume element 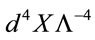 is locally invariant, the metric
is locally invariant, the metric 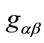 does not appear in minimally coupled matter actions.
does not appear in minimally coupled matter actions.
Note that this prescription allows for a universal coupling of any matter field to the gauge fields of the theory treating them as scalars in inner space.
Technically no fundamentally new difficulties arise and the relevant matter terms are simply added to the formulae for both the Lagrangian and Hamiltonian gauge field theories of the group of volume-preserving diffeomorphisms of 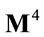 [3].
[3].
8. Conclusions
In this paper we have started to explore the consequences of viewing the gravitational energy momentum 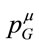 as different by its very nature from the inertial energymomentum
as different by its very nature from the inertial energymomentum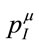 , accepting their observed numerical equality as accidential.
, accepting their observed numerical equality as accidential.
This view has motivated us to add new field degrees of freedom allowing to represent an inner translation group in field space in order to generate a new conserved fourvector through Noether’s theorem which we interpret as gravitational energy momentum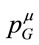 .
.
Gauging this inner translation group has naturally led to the gauge field theory of the group of volume-preserving diffeomorphisms of 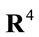 with unimodular Jacobian, at the classical level, thereby generalizing nonAbelian gauge field theories with a finite number of gauge fields. In contrast to that case, in order to gauge coordinate transformations of an inner
with unimodular Jacobian, at the classical level, thereby generalizing nonAbelian gauge field theories with a finite number of gauge fields. In contrast to that case, in order to gauge coordinate transformations of an inner 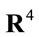 we had to introduce an uncountably infinite number of gauge fields labeled by
we had to introduce an uncountably infinite number of gauge fields labeled by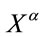 , the inner coordinates of the fields on which we represent the global and local gauge groups.
, the inner coordinates of the fields on which we represent the global and local gauge groups.
This has not brought along fundamental difficulties as far as the definitions of the covariant derivative, the gauge field and the field strength operators are concerned. As the components of these operators are vectors in inner space we then introduced a flat metric 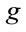 on
on 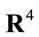 in order to allow for coordinate-invariant contractions of inner space indices, making it the inner Minkowski space
in order to allow for coordinate-invariant contractions of inner space indices, making it the inner Minkowski space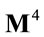 .
.
Potentially fundamental difficulties, however, have arisen in the definition of other crucial elements of the theory—such as the trace operation in the definition of the gauge field action. Tr turned out to be a potentially divergent integral over the non-compact inner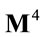 . Accordingly we had to defined the trace operation using the scale parameter
. Accordingly we had to defined the trace operation using the scale parameter 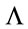 inherent to the theory as a cutoff and have shown that the theories for different
inherent to the theory as a cutoff and have shown that the theories for different 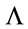 are in fact related to each other by an additional global inner scale symmetry of the theory.
are in fact related to each other by an additional global inner scale symmetry of the theory.
We then have proposed—with consistent quantization in view—a covariant, minimal gauge field Lagrangian. Next, we have derived the field equations and shown their independence of the inner metric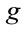 . Finally we have determined the conserved Noether currents and charges belonging to the inner and spacetime symmetries of the theory including the energy-momentum density of the gauge fields.
. Finally we have determined the conserved Noether currents and charges belonging to the inner and spacetime symmetries of the theory including the energy-momentum density of the gauge fields.
The natural framework to consistently deal with gauge fixing, to implement the constraints and to both define a classical field theory and prepare its path integral quantization is the Hamiltonian formalism for which we have derived the theory’s Hamiltonian and the corresponding Hamiltonian dynamics through choosing Cartesian coordinates with a Minkowski metric in inner space—partially fixing a gauge—and imposing on top the axial gauge condition to fully fix the gauge.
A key condition for the viability of the theory is the positivity of the Hamiltonian. A careful analysis relates 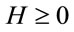 to a quite natural restriction for the support of the Fourier-transformed gauge fields being limited to the forward and backward light cones in inner
to a quite natural restriction for the support of the Fourier-transformed gauge fields being limited to the forward and backward light cones in inner 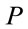 -space. In addition, this analysis uncovers a set of two times six unconstrained independent canonical variables obeying the usual Poisson brackets with which the theory can be formulated and which will serve as the starting point for quantization [10].
-space. In addition, this analysis uncovers a set of two times six unconstrained independent canonical variables obeying the usual Poisson brackets with which the theory can be formulated and which will serve as the starting point for quantization [10].
The result is a classical field theory formulated on flat four-dimensional Minkowski spacetime which is invariant under local 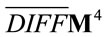 gauge transformations and at most quartic in the fields—a perfect candidate for a renormalizable, asymptotically free quantum field theory.
gauge transformations and at most quartic in the fields—a perfect candidate for a renormalizable, asymptotically free quantum field theory.
In two separate papers we show that the present theory encompasses classical gravitation at the Newtonian level in a natural way [9] and that the quantized gauge theory of volume-preserving diffeomorphisms of 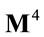 is re-normalizable and asymptotically free at one-loop [10].
is re-normalizable and asymptotically free at one-loop [10].
REFERENCES
- L. O’Raifeartaigh, “Group Structure of Gauge Theories,” Cambridge University Press, Cambridge, 1986.
- S. Weinberg, “The Quantum Theory of Fields I,” Cambridge University Press, Cambridge, 1995. doi:10.1017/CBO9781139644167
- S. Weinberg, “The Quantum Theory of Fields II,” Cambridge University Press, Cambridge, 1996. doi:10.1017/CBO9781139644174
- C. Wiesendanger, Classical and Quantum Gravity, Vol. 12, 1995, p. 585; C. Wiesendanger, Classical and Quantum Gravity, Vol. 13, 1996, p. 681 and references therein. doi:10.1088/0264-9381/13/4/008
- C. Rovelli, “Quantum Gravity,” Cambridge University Press, Cambridge, 2004.
- C. Kiefer, “Quantum Gravity,” Oxford University Press, Oxford, 2007. doi:10.1093/acprof:oso/9780199212521.001.0001
- C. Wiesendanger, Physical Review D, Vol. 80, 2009, Article ID: 025018. doi:10.1103/PhysRevD.80.025018
- C. Wiesendanger, Physical Review D, Vol. 80, 2009, Article ID: 025019. doi:10.1103/PhysRevD.80.025019
- C. Wiesendanger, “II—Conservation of Gravitational Energy Momentum and Poincaré-Covariant Classical Theory of Gravitation,” arXiv:1103.0349 [math-ph].
- C. Wiesendanger, “III—Conservation of Gravitational Energy Momentum and Renormalizable Quantum Theory of Gravitation,” arXiv:1103.1012 [math-ph].
Appendix
Notations and Conventions
Generally, 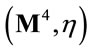 denotes the four-dimensional Minkowski space with metric
denotes the four-dimensional Minkowski space with metric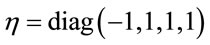 , small letters denote spacetime coordinates and parameters and capital letters denote coordinates and parameters in inner space.
, small letters denote spacetime coordinates and parameters and capital letters denote coordinates and parameters in inner space.
Specifically, 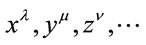 denote Cartesian spacetime coordinates. The small Greek indices
denote Cartesian spacetime coordinates. The small Greek indices 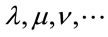 from the middle of the Greek alphabet run over 0, 1, 2, 3. They are raised and lowered with
from the middle of the Greek alphabet run over 0, 1, 2, 3. They are raised and lowered with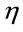 , i.e.
, i.e. 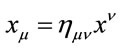 etc. and transformed covariantly w.r.t. the Lorentz group
etc. and transformed covariantly w.r.t. the Lorentz group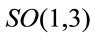 . Partial differentiation w.r.t to
. Partial differentiation w.r.t to 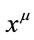 is denoted by
is denoted by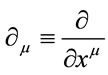 . Small Latin indices
. Small Latin indices 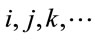 generally run over the three spatial coordinates 1, 2, 3 [2].
generally run over the three spatial coordinates 1, 2, 3 [2].
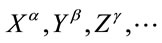 denote inner coordinates and
denote inner coordinates and 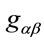 the flat metric in inner space with signature
the flat metric in inner space with signature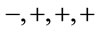 . The metric transforms as a contravariant tensor of Rank 2 w.r.t.
. The metric transforms as a contravariant tensor of Rank 2 w.r.t.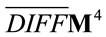 . Because
. Because 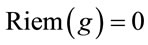 we can always globally choose Cartesian coordinates and the Minkowski metric
we can always globally choose Cartesian coordinates and the Minkowski metric 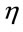 which amounts to a partial gauge fixing to Minkowskian gauges. The small Greek indices
which amounts to a partial gauge fixing to Minkowskian gauges. The small Greek indices 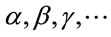 from the beginning of the Greek alphabet run again over 0, 1, 2, 3. They are raised and lowered with
from the beginning of the Greek alphabet run again over 0, 1, 2, 3. They are raised and lowered with
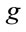 , i.e.
, i.e. 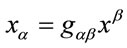 etc. and transformed as vector indices w.r.t.
etc. and transformed as vector indices w.r.t.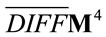 . Partial differentiation w.r.t to
. Partial differentiation w.r.t to 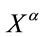 is denoted by
is denoted by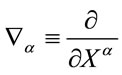 .
.
The same lower and upper indices are summed unless indicated otherwise.

