Journal of Modern Physics
Vol.4 No.6(2013), Article ID:32956,3 pages DOI:10.4236/jmp.2013.46102
Study of Effective Edge Safety Factor Using Analytical Solution of Grad-Shafranov Equation for Circular Cross Section Tokamak
Department of Physics, COMSATS Institute of Information Technology, Lahore, Pakistan
Email: dr.muha.asif@gmail.com
Copyright © 2013 M. Asif. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received April 5, 2013; revised May 7, 2013; accepted June 2, 2013
Keywords: Horizontal Displacement; Tokamak
ABSTRACT
In this work, we present effective edge safety factor using analytical solution of the Grad-Shafranov equation based on expansion of free functions of first order and magnetic probes for circular cross section HT-7 tokamak.
1. Introduction
The majority of research efforts in the area of controlled nuclear fusion, especially in tokamak research, are focused on confinement of hot plasmas by means of strong magnetic fields. Control of plasma position plays an important role in plasma confinement [1-16], and the achievement of optimized tokamak plasma operation. Therefore, plasma equilibrium study is one of the fundamental problems in magnetically confined plasmas. In tokamak equilibrium studies, there are many available experimental methods, and analytical solutions [1-15] for the steady state magnetohydrodynamic (MHD) equations, in particular, the Grad-Shafranov equation [17-19]. In this work, we present effective edge safety factor using analytical solutions [17-19] of the Grad-Shafranov equation [17] based on expansion of free functions of first order and magnetic probes for circular cross section HT-7 tokamak [16] (see Table 1).
2. Extended Grad-Shafranov Equation
Maxwell’s equations together with the force balance equation from MHD equations, in the cylindrical coordinates (R, Z) reduce to the two-dimensional, nonlinear, elliptic partial differential equation, or Grad-Shafranov equation [4]: As in the linear case, the procedure to derive the Grad-Shafranov equation can be followed obtaining an extended Grad-Shafranov equation [17-25]
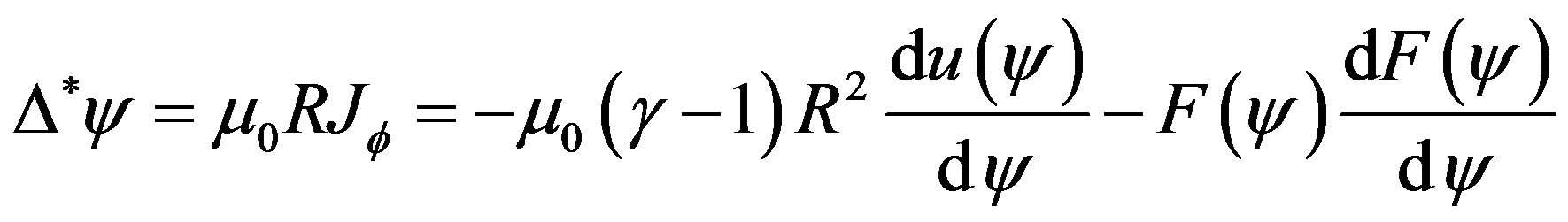 (1)
(1)
where  is
is
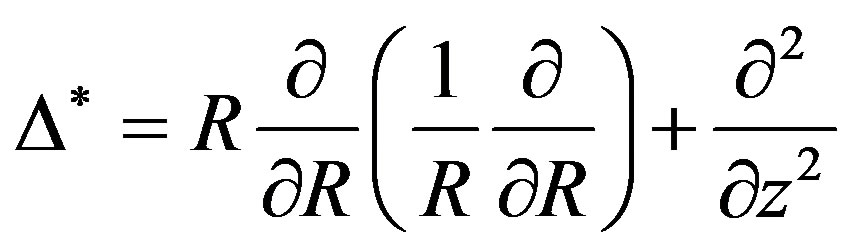 (2)
(2)
The internal energy in this extended Grad-Shafranov equation is a function of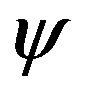 . The
. The 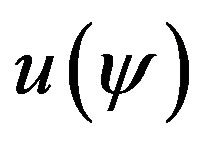 and
and 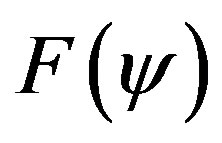 are two free functions, and where
are two free functions, and where 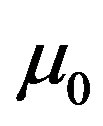 and
and  are the vacuum permeability and plasma current density respectively.
are the vacuum permeability and plasma current density respectively.
3. Effective Edge Safety Factor by Solution of GSE
For circular cross section HT-7 Tokamak [16,26] (see Table 1), which is the ohmically heated tokamak, the Grad-Shafranov equation [17,27-28], is solved by formally expanding as follows [4,29]:
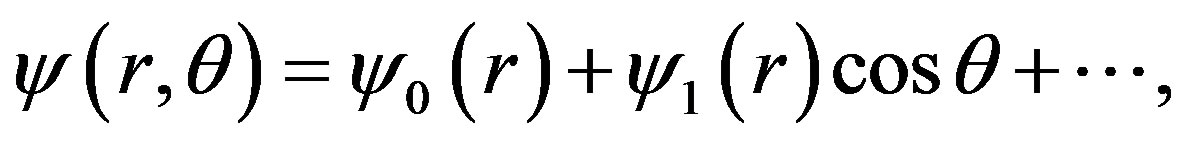 (3)
(3)
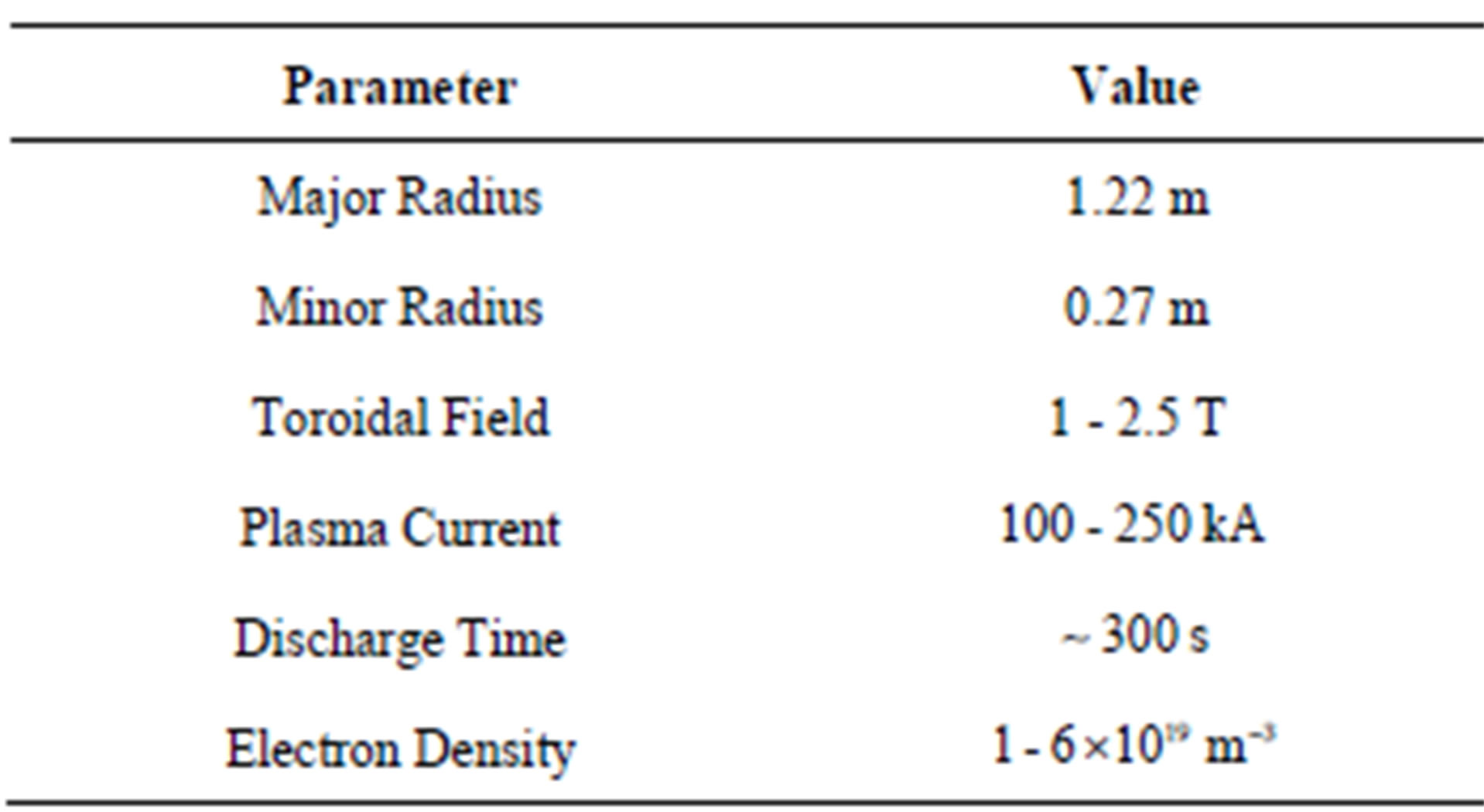
Table 1. Parameter of the HT-7 tokamak.
 (4)
(4)
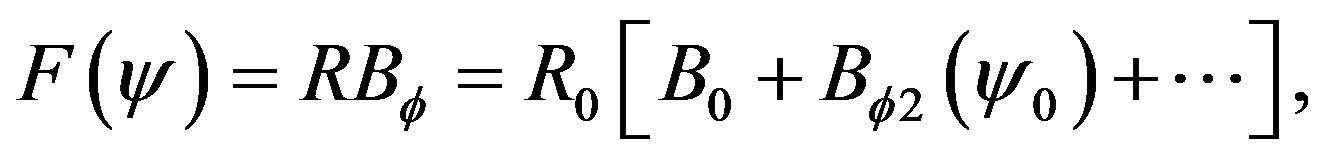 (5)
(5)
where 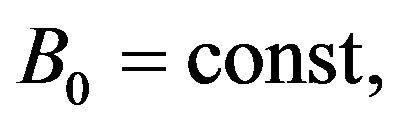 is the vacuum toroidal field at
is the vacuum toroidal field at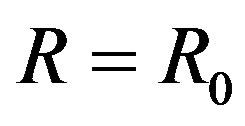 ,
, 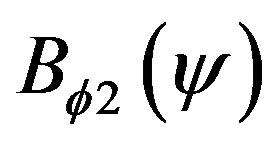 is a new free function replacing
is a new free function replacing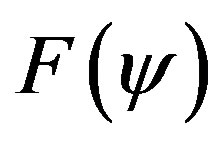 . In the first order solution or toroidal force balance approximation and if plasma were surrounded by a perfectly conducting shell located at
. In the first order solution or toroidal force balance approximation and if plasma were surrounded by a perfectly conducting shell located at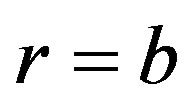 , then first order flux function [29] is:
, then first order flux function [29] is:
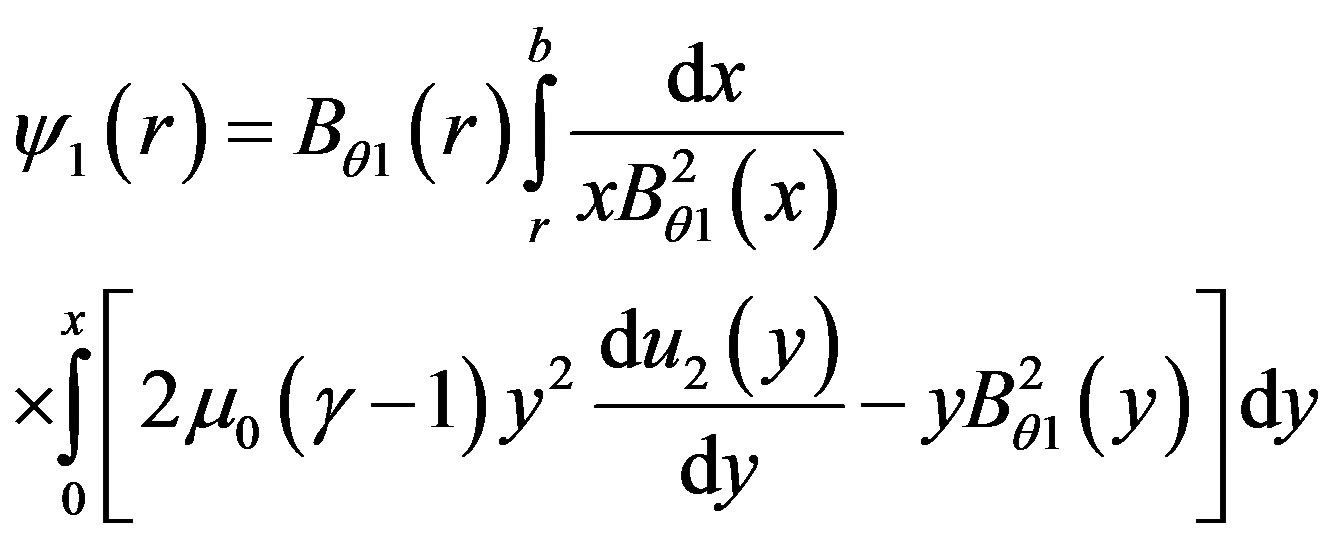 (6)
(6)
If there are external coils to produce vertical magnetic field, the boundary condition on the flux function is modified so that we have:
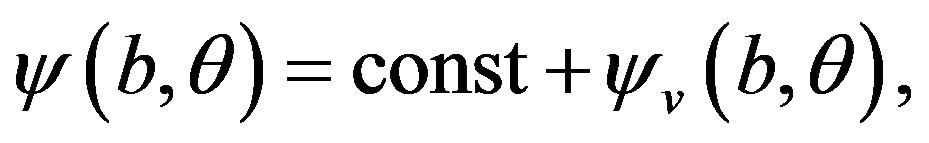 (7)
(7)
where 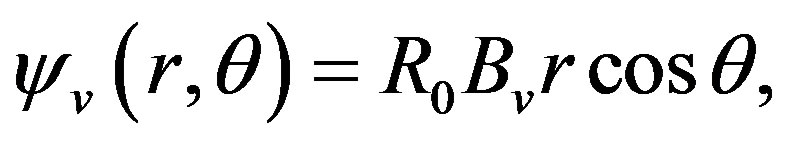 is the flux function due to external vertical field coils and therefore the full toroidal correction to
is the flux function due to external vertical field coils and therefore the full toroidal correction to 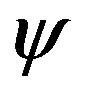 is:
is:
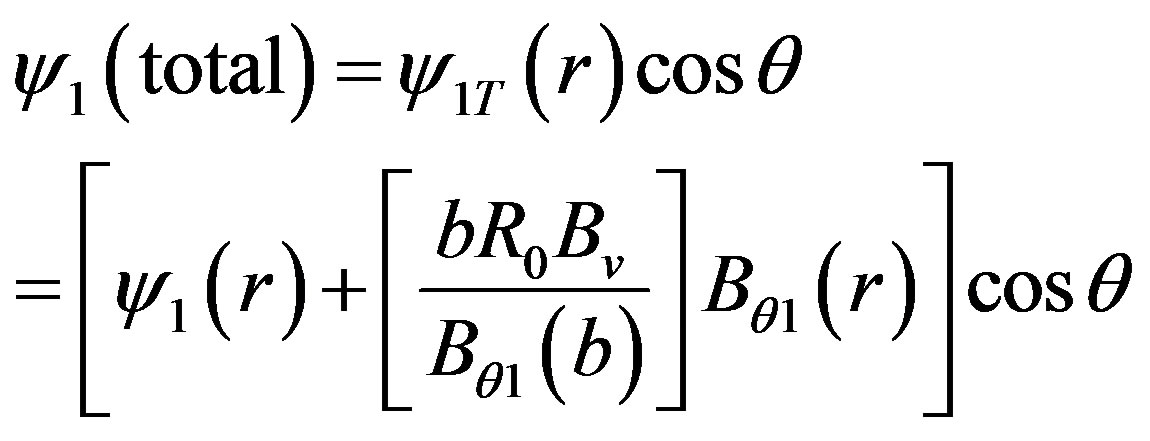 (8)
(8)
The shift of the plasma column center from the geometrical center of vacuum chamber is given by [29]:
 (9)
(9)
where .
.
Therefore, the first relation for plasma position [29] is
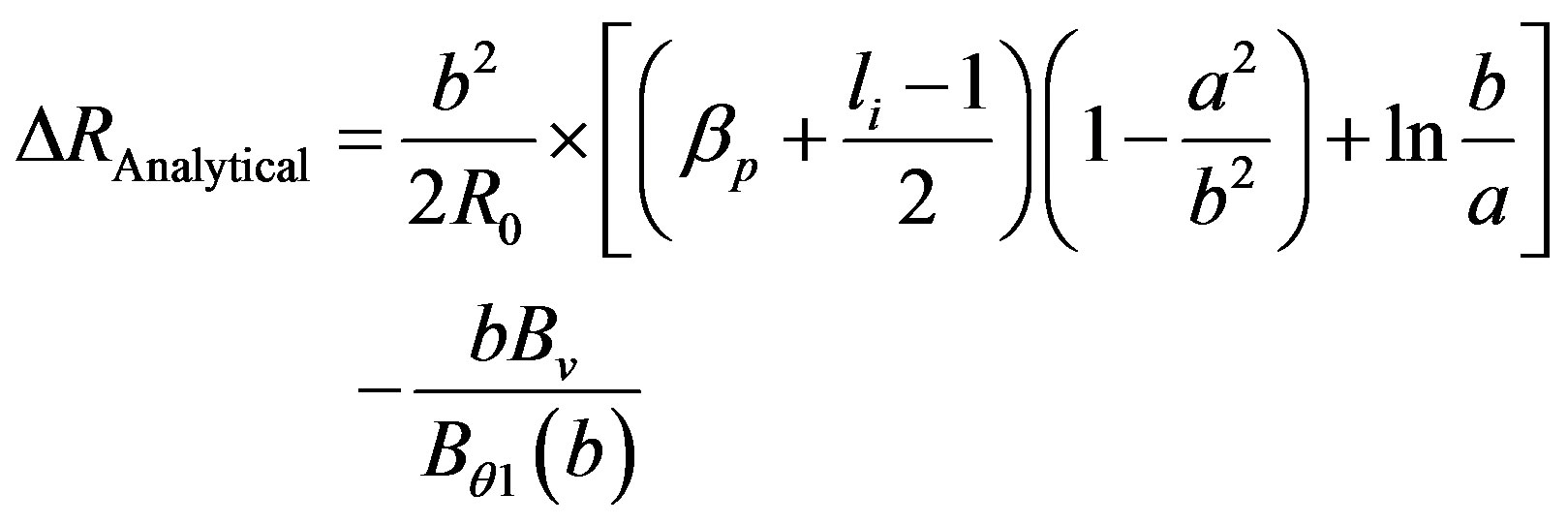 (10)
(10)
where 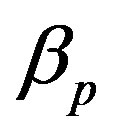 is the poloidal beta,
is the poloidal beta, 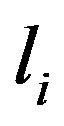 is the internal inductance of the plasma, and
is the internal inductance of the plasma, and 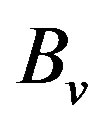 is the average vertical magnetic field over the vacuum chamber. We can find
is the average vertical magnetic field over the vacuum chamber. We can find 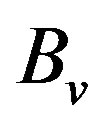 from saddle sine coil [22] and the sum of the poloidal beta and half the plasma internal inductance expression
from saddle sine coil [22] and the sum of the poloidal beta and half the plasma internal inductance expression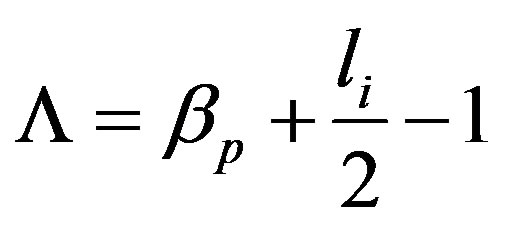 , where (
, where ( is Shafranov pa-
is Shafranov pa-
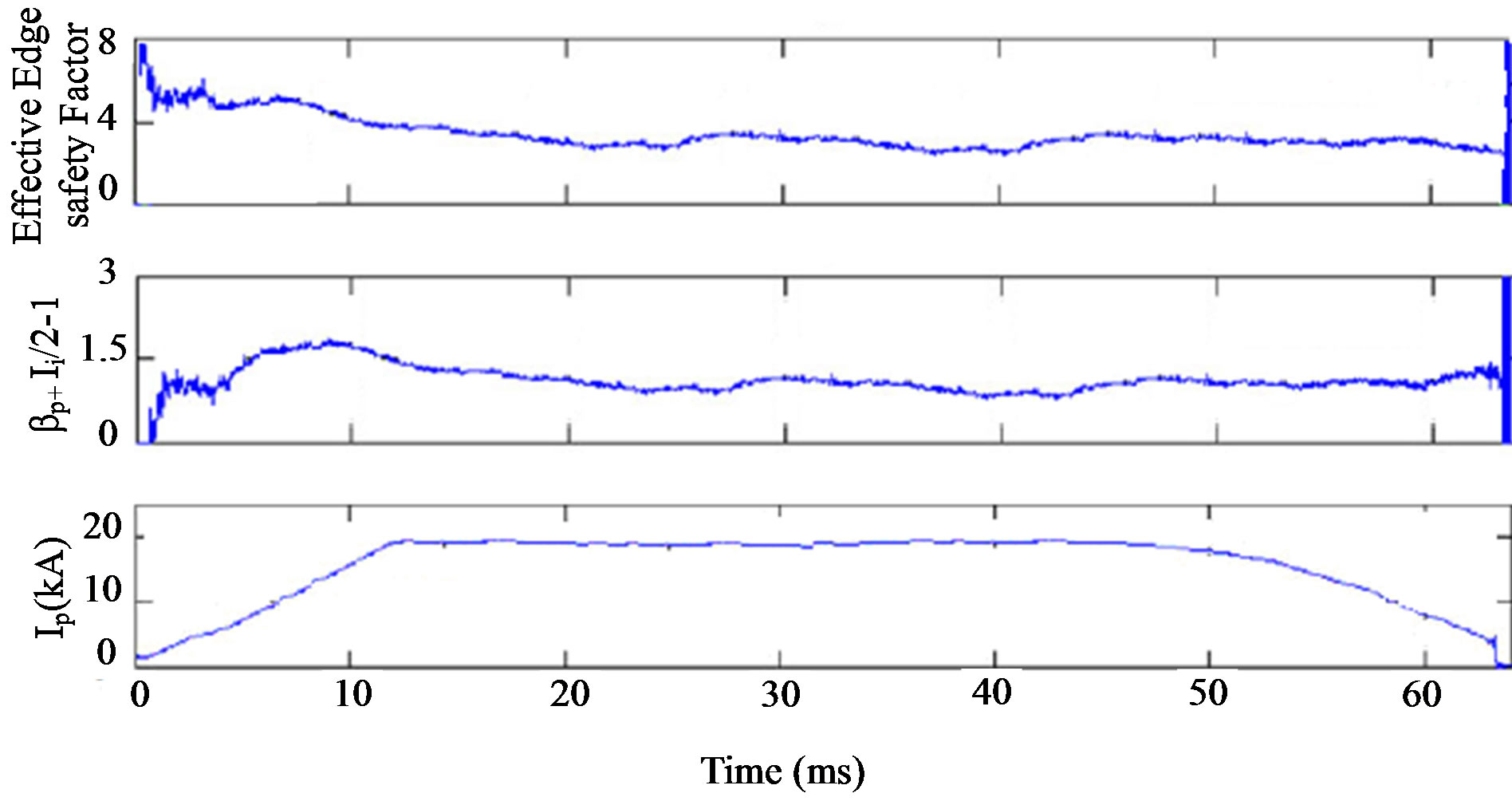
Figure 1. Edge safety factor obtained for circular cross section HT-7 tokamak by the GSE solution and magnetic probes.
rameter) from magnetic coils measurement [22-25,30] using following equations
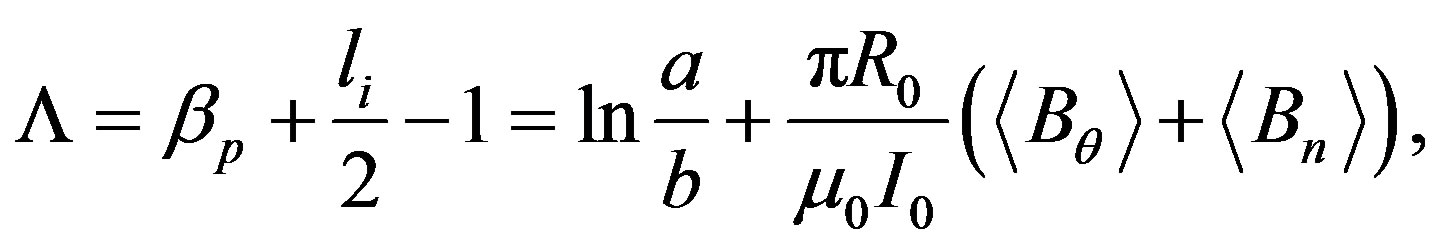 (11)
(11)
where
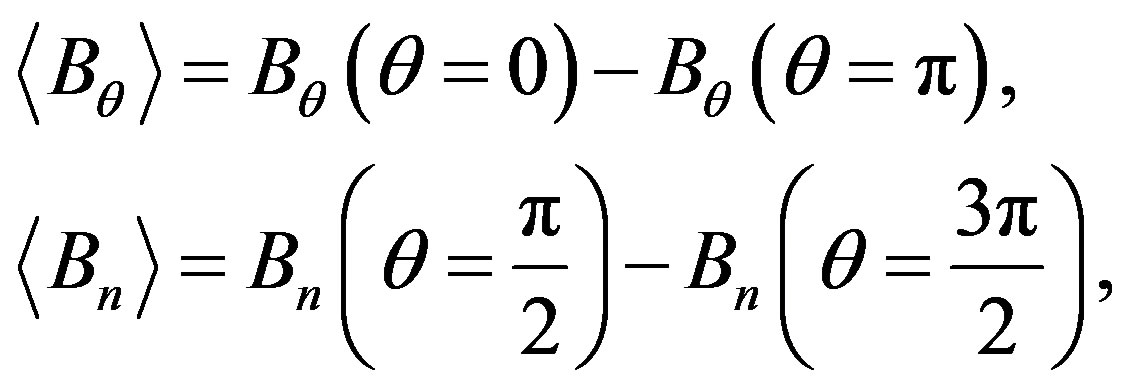 (12)
(12)
We measured these local magnetic fields with magnetic probes [22] at above angles.
Therefore the effective edge safety factor at the plasma edge is given by [31]:
 (13)
(13)
According to this relation, and also the value of Shafranov parameter which measured with magnetic probe we plotted time history of the effective edge safety factor in target shot for circular cross section HT-7 tokamak, as shown in Figure 1.
4. Conclusion
We have determined the effective edge safety factor using analytical solution of the Grad-Shafranov equation based on expansion of free functions of first order and magnetic probes for circular cross section HT-7 tokamak.
REFERENCES
- A. S. Elahi and M. Ghoranneviss, Physica Scripta, Vol. 80, 2009, Article ID: 0555024.
- A. R. Rad and M. Ghoranneviss, Physica Scripta, Vol. 81, 2010, Article ID: 045502.
- A. S. Elahi and M. Ghoranneviss, Physica Scripta, Vol. 82, 2010, Article ID: 025502.
- J. P. Freidberg, “Ideal MHD,” Clarendon, Oxford, 1987.
- L. Guazzotto and J. P. Freidberg, Physics Plasmas, Vol. 14, 2007, Article ID: 112508.
- M. Shimada, et al., Nuclear Fusion, Vol. 47, 2007, pp. S1-S17. doi:10.1088/0029-5515/47/6/S01
- C. V. Atanasiu, S. Günter, K. Lackner and I. G. Miron, Physics Plasmas, Vol. 14, 2004, p. 3510.
- G. S. Lee, et al., Nuclear Fusion, Vol. 41, 2001, pp. 1515-1523. doi:10.1088/0029-5515/41/10/318
- S.-H. Seo, Physics Plasmas, Vol. 16, 2009, Article ID: 032501.
- S. G. Lee, J. G. Bak, E. M. Ka, J. H. Kim and S. H. Hahn, Review of Scientific Instruments, Vol. 79, 2008, Article ID: 10F117.
- A. J. H. Donné, et al., Nuclear Fusion, Vol. 47, 2007, pp. S337-S384. doi:10.1088/0029-5515/47/6/S07
- F. Najmabadi and the ARIES Team, Fusion Engineering and Design, Vol. 65, 2003, pp. 143-164. doi:10.1016/S0920-3796(02)00302-2
- L. Guazzotto, R. Betti, J. Manickam and S. Kaye, Physics Plasmas, Vol. 11, 2004, p. 604.
- A. S. Elahi, M. Ghoranneviss, M. Emami and A. R. Rad, Journal of Fusion Energy, Vol. 28, 2009, pp. 346-349. doi:10.1007/s10894-009-9198-x
- C. V. Atanasiu, Proceedings of 30th EPS Conference on Controlled Fusion and Plasma Physics, Vol. 27A, ECA, St Petersburg, 2003, p. 2104.
- M. Asif, X. Gao, J. G. Li and B.N. Wan, Physics Letters A, Vol. 336, 2005, pp. 61-65. doi:10.1016/j.physleta.2005.01.004
- M. Asif, Magnetohydrodynamics, Vol. 47, 2011, pp. 11- 16.
- M. Asif, Magnetohydrodynamics, Vol. 48, 2012, pp. 485- 492.
- M. Asif, Modern Physics Letters B, Vol. 26, 2012, pp. Article ID: 1250117.
- S. B. Zheng, A. J. Wootton and E. R. Solano, Physics Plasmas, Vol. 3, 1996, pp. 1176-1178. doi:10.1063/1.871772
- A. R. Rad, M. Emami, M. Ghoranneviss and A. S. Elahi, Journal of Fusion Energy, Vol. 28, 2010, pp. 73-75. doi:10.1007/s10894-009-9236-8
- B. Shen, Y. W. Sun, B. N. Wan and J. P. Qian, Review of Scientific Instruments, Vol. 78, 2007, Article ID: 093501.
- V. S. Mukhovatov and V. D. Shafranov, Nuclear Fusion, Vol. 11, 1971, pp. 605-634. doi:10.1088/0029-5515/11/6/005
- H. Ninomiya and N. Suzuki, Japanese Journal of Applied Physics, Vol. 21, 1982, pp. 1323-1327. doi:10.1143/JJAP.21.1323
- M. Asif, X. Gao, J. G. Li and B. N. Wan, Physics Letters A, Vol. 342, 2005, pp. 175-180. doi:10.1016/j.physleta.2005.05.032
- M. Asif, et al., Physics Plasmas, Vol. 12, 2005, Article ID: 082502.
- L. S. Solovyev, Journal of Experimental and Theoretical Physics, Vol. 26, 1968, p. 400.
- A. R. Rad and M. Ghoranneviss, Journal of Fusion Energy, Vol. 32, 2013, pp. 405-409. doi:10.1007/s10894-012-9583-8
- S. Elahi, et al., Journal of Fusion Energy, Vol. 28, 2009, pp. 385-389. doi:10.1007/s10894-009-9207-0
- M. Asif and X. Gao, Brazilian Journal of Physics, Vol. 36, 2006, pp. 190-193. doi:10.1590/S0103-97332006000200011
- T. N. Todd, Proceedings of the 2nd European Tokamak Programme Workshop, European Physical Society, SaultLes-Chartreux, 1983, p. 123.

