ABSTRACT

It is shown that the criterion of incompressibility applicable to any medium, contradicts to the real meaning of this term. On the basis of expression of speed of sound in inhomogeneous medium and generalized equation of continuity of mass obtained in papers [1,2] respectively, it is proved that so called internal gravitation waves do not exist in nature. This concept appeared as a result of incorrect interpretation of incompressibility of medium. Correct understanding of criteria of compressibility or incompressibility leads to qualitatively new understanding of homogeneity or heterogeneity of medium, in particular—only strongly inhomogeneous medium can be incompressible while weakly inhomogeneous medium is always compressible. Besides, it is shown that in inhomogeneous media additional terms are added to known hydrodynamic (gas dynamic) correlations applicable to any medium which disappear at transfer to homogeneous model of medium.

1. Introduction

It is common knowledge that all researches that have been carried out in the sphere of gas and hydrodynamics so far were based on the assumption that the speed of sound in the medium is the speed of distribution of perturbation of density which occurs as a result of change of the mass of the given volume of liquid at constant entropy and is determined by the formula

.

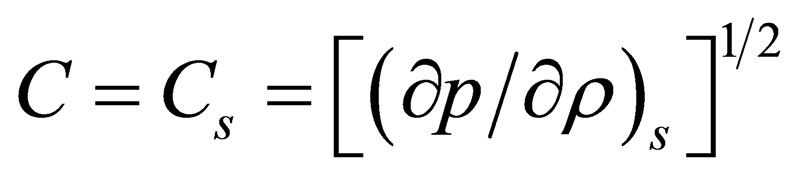The medium is considered incompressible 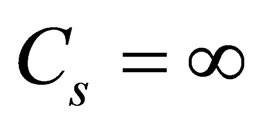if or if, where is a characteristic speed of liquid motion. From this it follows that in the course of investigation of wave processes (except sound one), any stationary medium can be considered incompressible. Such approach leads to falling of the equation of state of medium connecting perturbed values of density and pressure from the system of hydrodynamic equations. Significance of this equation is also that it contains thermodynamic parameters of medium and in case of its absence it is unclear, which medium is considered. Besides, it is obvious that in this case perturbation of density does not occur and distribution of wave is impossible. That is why many gas and hydrodynamic tasks like the tasks of surface gravity wave and internal wave are solved incorrectly [3].

The above determination of the speed of sound is fair only for homogeneous medium, when 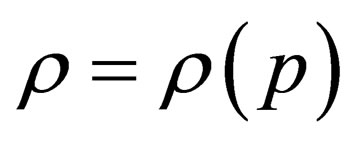and bears no relation to reality. In fact, any medium in gravitational field is inhomogeneous to a greater or lesser extent and therefore 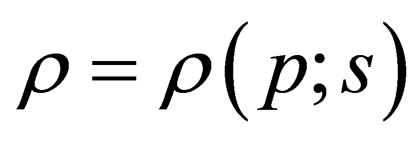[4], where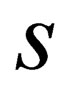—entropy. In inhomogeneous medium, the speed of sound is determined by the formula 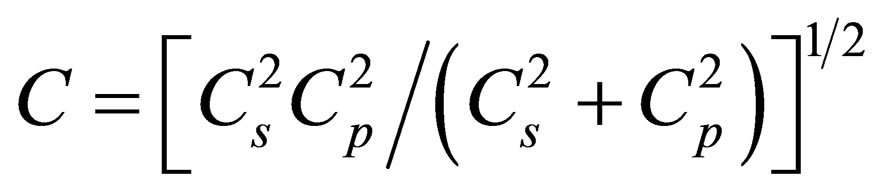[1]where 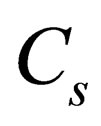is adiabatic speed of sound, while is isobaric speed of sound which in homogeneous medium equals to infinity and therefore 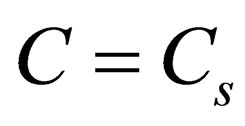i.e. homogeneous medium, or to be more exact—weakly inhomogeneous medium is always compressible. If conversely, when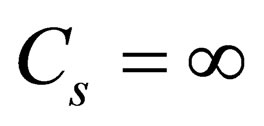, , 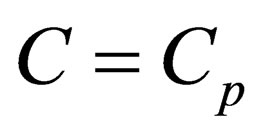and the strongly inhomogeneous medium is always incompressible. In this approach the equation of condition of medium in the system of hydrodynamic (gas dynamic) equations presents in any case which provides opportunity to take account of its hydrodynamic parameters in disperse equation. Thus, compressibility or incompressibility of medium should be determined from correlation of speeds and.

In the first section of the paper, based on recently published calculations [2] we demonstrate that the equation of mass continuity, which was considered universal, needs to be developed in inhomogeneous medium, which drastically changes the criterion of his compressibility or incompressibility. Having applied new interpretation of these criteria, in the second section we show that nature is not acquainted with the commonly known inner gravity waves in their existing understanding. In truth these waves are sound waves in strongly inhomogeneous liquid. In the third section of the paper we exemplify how the known gas and hydrodynamic correlations change when the effect of inhomogeneous medium is taken into consideration.

2. Equation of Mass Continuity and Criterion of Compressibility (Incompressibility) of Medium

From determination of density it follows that its change in time is calculated according to the formula [2]

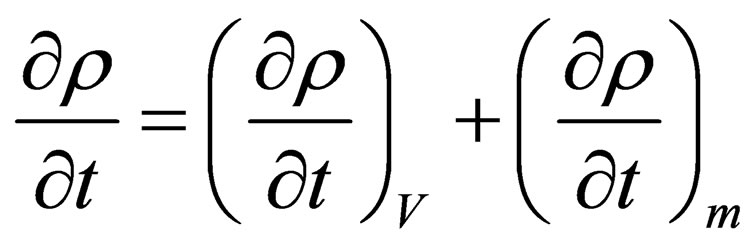(1.1)

The first summand in the right part (1.1) determines change of density at constant volume, which may occur only at constant entropy at the expense of difference of liquid flows through the surface limiting this volume. Therefore

(1.2)

where is speed of fluid. On the other hand

(1.3)

Expression, connecting perturbation of density and pressure at constant volume, has the dimension contrary to the dimension of square of speed, and as it turned out, its reciprocal value complies with the equation of sound wave in homogeneous medium when [3-5]. Therefore, the expression

(1.4)

is called speed of sound in medium. Curiously enough, in this connection it is not mentioned that the medium is homogeneous and it is assumed that such determination of speed of sound is fair for any medium, which leads to paradoxical results. We will demonstrate it by the example of the Earths’ atmosphere. Considering the air as ideal gas, (J/К—Boltzmann’s constant,—concentration of molecules of air,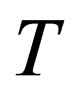— absolute temperature) in which dependence between pressure and density in adiabatic process is defined by the following correlation

(1.5)

where 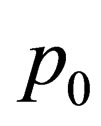and 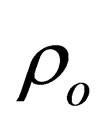are initial values of pressure and density, and an adiabatic index is ratio of thermal capacities (specific heath), for air in presence of constant pressure and volume respectively, from (1.5) for speed of sound following expression is derived:

(1.6)

Here J/mol∙K is a gas constant, is mass of one air molecule and kg/mol—mass of one mol air. Speed of sound in the whole atmosphere is calculated according to formula (1.6) [5], from which it follows that it depends only on the temperature and does not depend on altitude i.e. on density. It means that at sea level and at altitude, where density of atmosphere falls 10⁷ times, under the same temperature sound speeds must have similar meanings, which is impossible. In paper [1] it is demonstrated that sound speed in the Earth atmosphere with account of its heterogeneity should be determined by the formula

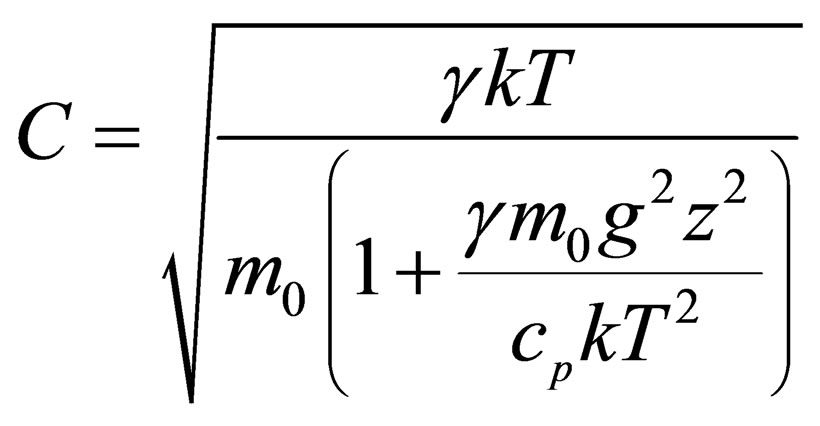(1.7)

which succeeds to be a substitution to the mentioned in introduction formula of values 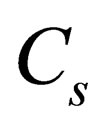from (1.6) and, physical meaning of which will be determined below. We see that sound speed in the Earth atmosphere is obviously dependent on altitude (density) and when, i.e. on the assumption of homogeneity of atmosphere, formula (1.7) transfers into formula (1.6).

The second summand in the right part of (1.1) describes change of density of the substance of constant mass as a result of change of volume which, in turn, in absence of heat source, is possible only under change of entropy, which certainly occurs at mechanic oscillation of inhomogeneous media, i.e.

(1.8)

Having expressed 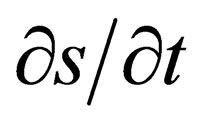from the adiabatic equation

(1.9)

we will obtain

(1.10)

The expression 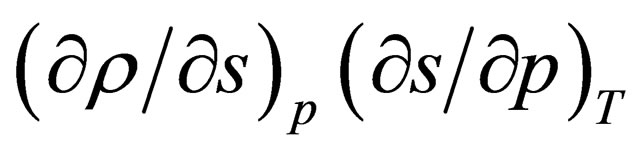has the dimension contrary to dimension of square of speed, therefore we can introduce expression

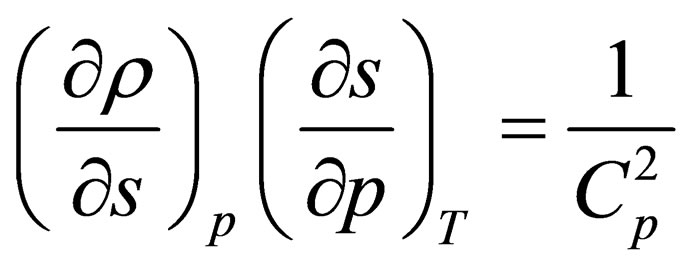(1.11)

where 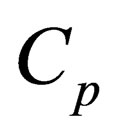may be called isobaric speed of sound. This value is the measure of inhomogenuity of medium and is characteristic for the speed of distribution of density perturbation related to isobaric change of volume of the given mass of substance. Applying (1.2), (1.10) and (1.11), from (1.1) we will ultimately obtain

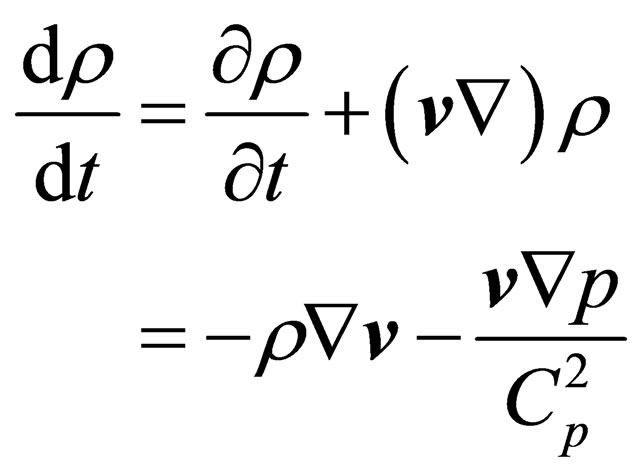(1.12)

Exactly this is the generalized equation of mass continuity which for homogeneous medium grades into the equation applied in the contemporary theory which was considered universal. Thus, compressibility of homogeneous medium cannot be ignored since from (1.12.) it follows that in such case change of density is impossible and consequently generation of wave processes is impossible.

Equation (1.12) can be written down as follows:

(1.13)

Integrating the Equation (1.13) on the given volume and applying Gauss-Ostrogradsky theorem on transformation of volume integral into superficial, from (1.13) we will obtain

(1.14)

where 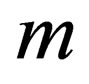is the liquid mass in the given volume and is the vector in magnitude equal to area of the element of surface limiting given volume and directed along outer normal.

The first summand in the right part of the Equation (1.14) determines change of mass in stagnant volume of liquid conditioned by difference of density flows through the surface limiting this volume while the second summand determines change of mass conditioned by motion of liquid within the volume itself due to natural pressure drop in inhomogeneous medium.

3. Sound Wave in Incompressible (Strongly Heterogeneous) Medium

As mentioned in the introduction, incorrect interpretation of significant concepts like compressibility or incompressibility leads to erroneous solution of many tasks of gas and hydro dynamics. As an example tasks of surface gravity wave and internal wave were cited. The first task was considered in paper [6] and it was shown that it was solved erroneously by Kelvin back in 1871. We admit that this paper is not deprived of shortcomings since by the time of its publication enough experience and knowledge of this problem had not yet been accumulated; however, appropriateness of criticism of Kelvin’s solution is doubtless. Here we will show that solution of the second task referred to in monograph [3] is also incorrect.

The authors call gravity waves within incompressible liquid located in the Earth’s gravitational field the internal wave. With respect to incompressibility they neglect change of density related to change of pressure and assume that change of density can only be isobaric, at the expense of change of entropy under mechanic oscillation of inhomogeneous medium, i.e.

(2.1)

It can easily be noticed that these are the waves we were talking about in the first section and the Equation (2.1) is identical to the Equation (1.8). Thereafter they write down linearized equations of motion and mass discontinuity in the form

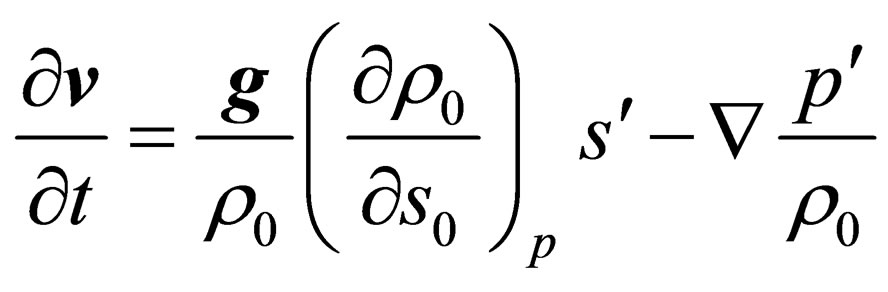(2.2)

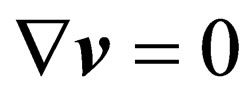(2.3)

Having presented all perturbed values of variable values in the form, from Equations (1.9), (2.2) and (2.3) they obtain

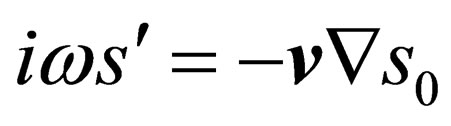(2.4)

(2.5)

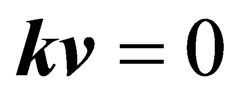(2.6)

Multiplying the Equation (2.5) by vector they receive

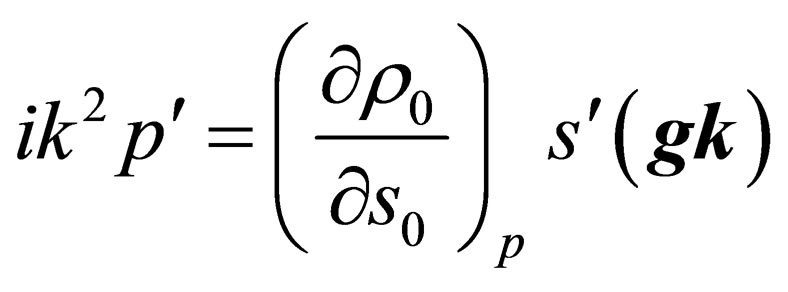(2.7)

From Equations (2.4), (2.5) and (2.7) can easily be obtained dispersive equation in the form

(2.8)

where

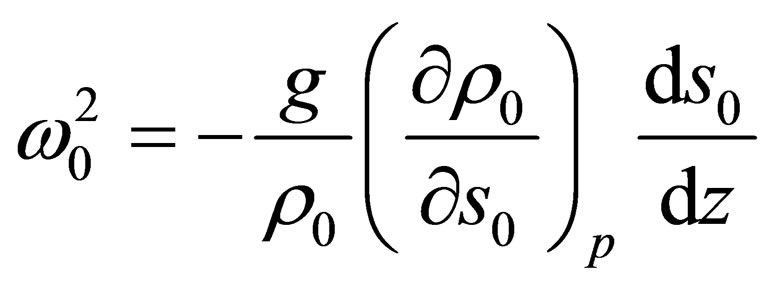(2.9)

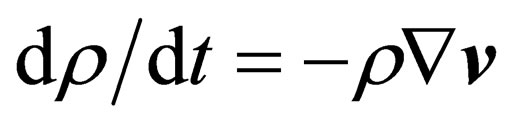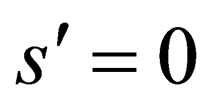and is angle between vector and axis. Thus, we get some kind of strange transverse wave, frequency of which depends only on direction of wave vector and it can be of any length. The reason of this paradox is that if in the equation of mass continuity the second summand related to heterogeneity of medium is not taken into consideration, then the condition means or following (2.1) and then all equations from which dispersive Equation (2.8) is obtained are nulling.

Thus, no special internal gravity wave exists. This is an ordinary sound wave in strongly inhomogeneous liquid which can be considered incompressible. Indeed, the system of linearized hydrodynamic equations in inhomogeneous medium takes the form [2]

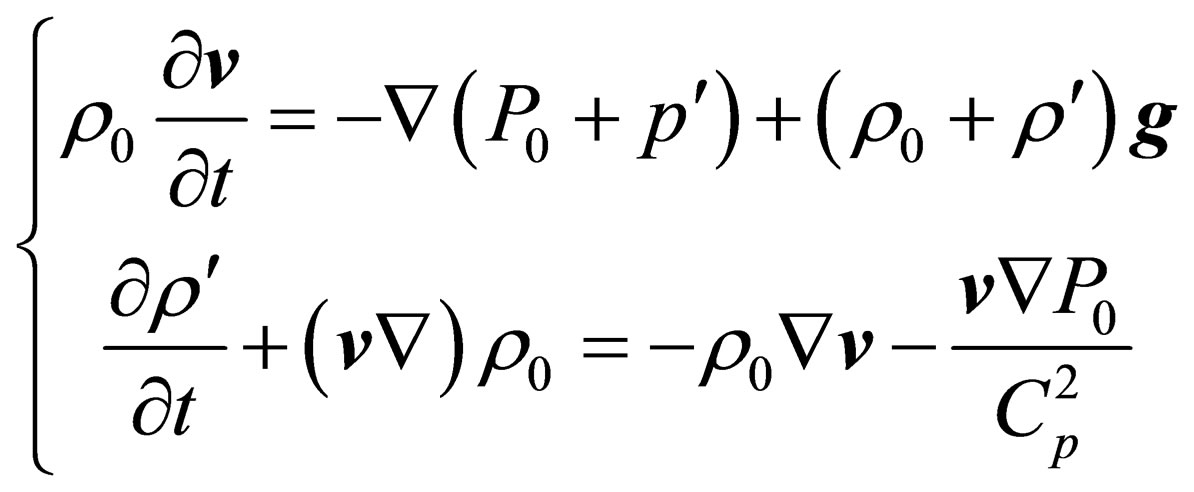(2.10)

Having applied medium balance equation in gravity filed 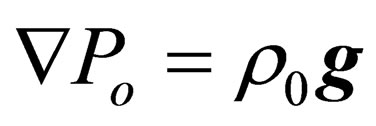and medium condition equation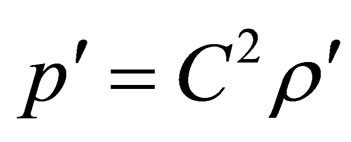, where, and also applying operator to the first equation of the system (2.10) and operator to the second one, it can easily be reduced to generalized equation of gravity waves (see [2])

(2.11)

Having assumed that the medium is strongly inhomogeneous 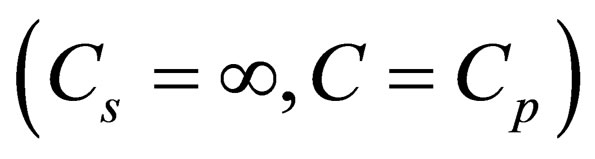and having neglected the third summands in respect to its smallness as compared to other summands, we will get

(2.12)

This equation is nothing else but equation of sound wave in strongly inhomogeneous liquid which is transverse with respect to oscillations of speed and longitudinal with respect to oscillations of density. It can be obtained directly from (2.10) having laid and.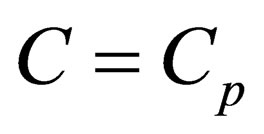

4. Calculation of Change of Densities of Energy and Impulse Inhomogeneous Liquid

Let us consider change of density of energy of immovable volume of liquid, i.e. calculate integral

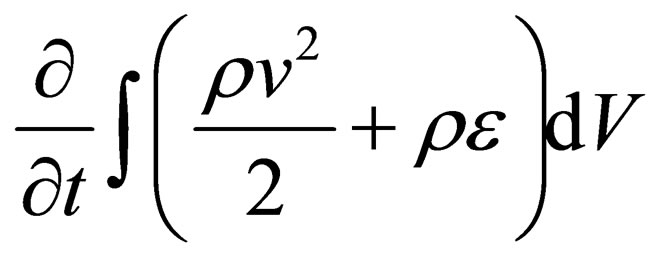(3.1)

where is inner energy of unit mass of liquid. First let’s calculate the first summand of (3.1)

(3.2)

Having applied the generalized equation of mass continuity (1.12) and the motion equation of Euler

(3.3)

from (3.2) we will obtain

(3.4)

Here the correlation is used. From the definition of differential of thermal function of mass unit of liquid 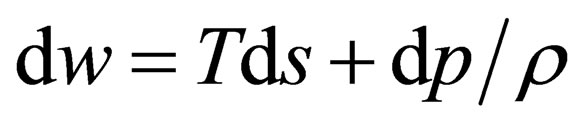we can write

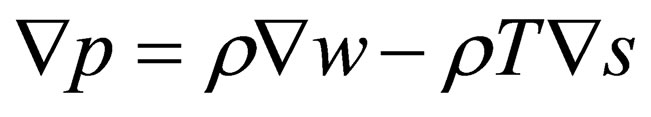(3.5)

Following which from (3.5) we will obtain

(3.6)

Having applied correlation, and Equation (1.9) from the second summand of (3.1) we will find out

(3.7)

Having considered (3.6) and (3.7) for (3.1) we will obtain

(3.8)

Having reconstructed the first volume integral in the right part of Equation (3.8) into superficial, we will ultimately obtain

(3.9)

Change of density of impulse in immovable volume of liquid is described by derivative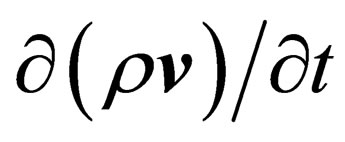. Let us consider this derivative in components, i.e.

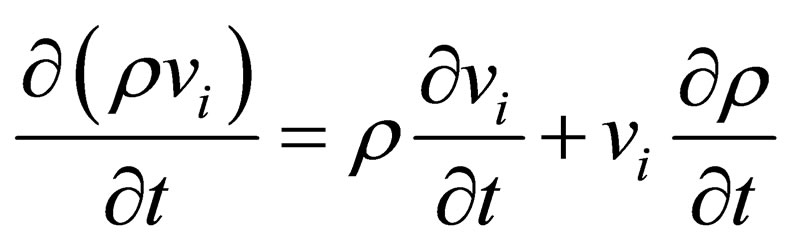(3.10)

and write Equations (1.12) and (3.3) in the form

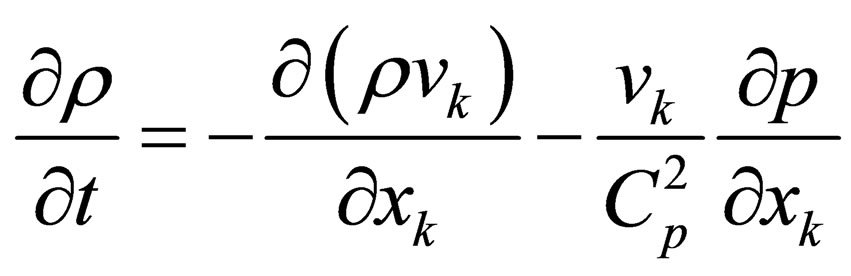(3.11)

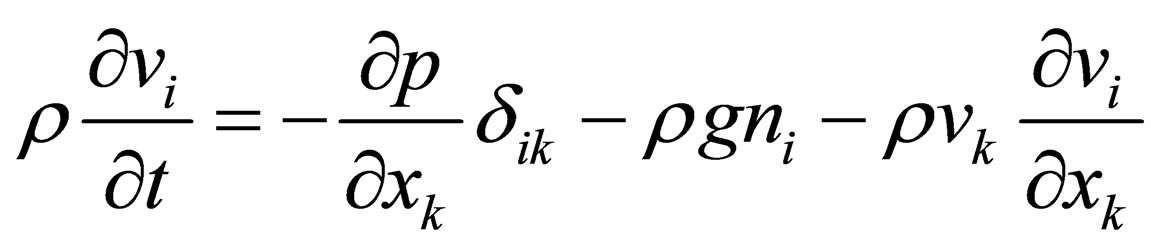(3.12)

where indexes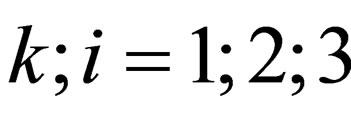, moreover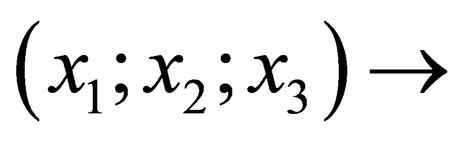 and—the components of unit vector directed along the axis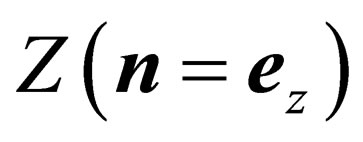. Having substituted (3.11) and (3.12) in (3.10) we will obtain

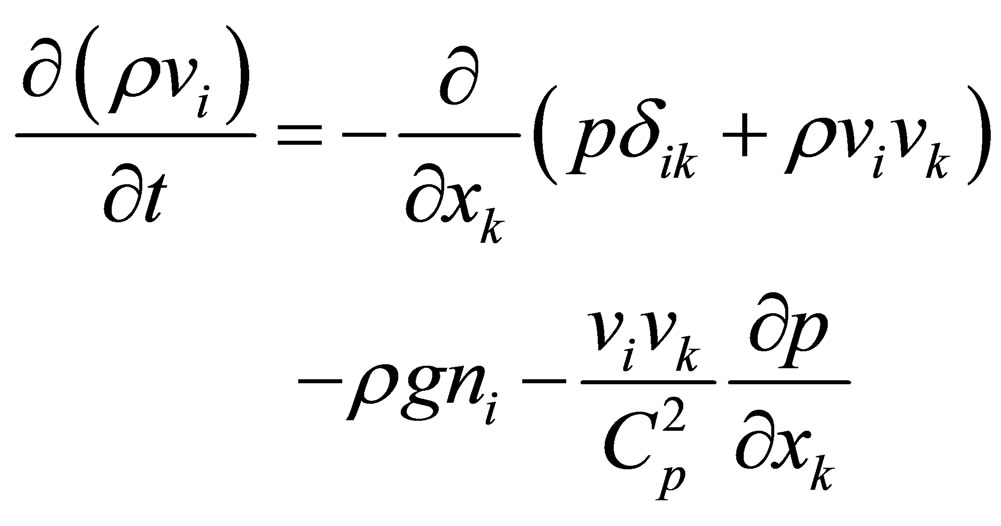(3.13)

Integration of Equation (3.13) according to volume gives

(3.14)

Correlations (3.9) and (3.14) for homogeneous liquids are obtained in the monograph [3], where only superficial integrals are presented. Consequently, change of density of energy and impulse in homogeneous liquids is influenced only by superficial processes. In inhomogeneous media speeds of change of densities of energy and impulse also depend on voluminous processes conditioned by work of external force and natural pressure fall inside the given volume.

5. Conclusion

Our reasoning conclusively proves that there are no ideally homogeneous media in nature. Any medium is inhomogeneous to a greater or lesser degree depending on correlation and. Moreover, homogeneity of medium does not mean that it is not influenced by external field of force. For instance, in the Earth atmosphere isobaric speed of sound is determined by formula

[1], from which it follows that at sea level 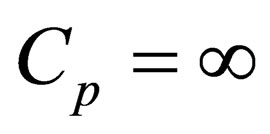, which is the criterion of ideally homogeneous medium, however, the formula includes acceleration of gravity. From our analysis it follows that, only strongly inhomogeneous medium when, can be incompressible, while weakly inhomogeneous medium when 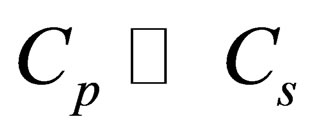can be compressible. Thus, the criterion of compressibility or incompressibility is determined not from correlation of and, but from correlation of and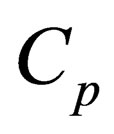, and the widespread opinion that compressibility (incompressibility) and homogeneity (heterogeneity) are independent concepts is erroneous. The reason of incorrectness discovered by us in the existing theory of internal gravity waves is that in the course of determination of criterion of incompressibility of medium it is insufficient to assume or which is the same. It is also necessary to take into consideration existence of isobaric sound speed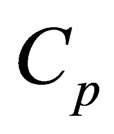, which represents the measure of heterogeneity of medium and is present in the equation of mass discontinuity. This approach evidences that in inhomogeneous media addition terms are added to known hydrodynamic (gas dynamic) correlations applicable to any medium which disappear at transfer to homogeneous model of medium.

REFERENCES