Journal of Modern Physics
Vol.4 No.3(2013), Article ID:28598,6 pages DOI:10.4236/jmp.2013.43045
Temperature Dependence of Density and Thermal Expansion of Wrought Aluminum Alloys 7041, 7075 and 7095 by Gamma Ray Attenuation Method
1Department of Physics, Kakatiya University, Warangal, India
2Varadha Reddy College of Engineering, Warangal, India
3CIC, Kakatiya University, Warangal, India
Email: ngopikrishna2012@yahoo.com
Received December 22, 2012; revised January 25, 2013; accepted February 4, 2013
Keywords: Density; Thermal Expansion; Linear Attenuation Coefficient; Mass Attenuation Coefficient
ABSTRACT
The gamma quanta attenuation studies have been carried out to determine mass attenuation coefficients of 7041, 7075 and 7095 wrought aluminum alloys. The temperature dependence of linear attenuation coefficient, density and thermal expansion of these wrought aluminum alloys in the temperature range 300 K - 850 K have been reported. The measurements were done by using a gamma ray densitometer designed and fabricated in our laboratory. The data on variation of density and linear thermal expansion with temperature have been represented by linear equations. Volume thermal expansion coefficients have been reported.
1. Introduction
Number of methods [1-13] have evolved for the determination of density and thermal expansion of solids at high temperature like Archimedean method, pycnometry, dilatometry, electromagnetic levitation, Method of maximal pressure in a gas bubble, method of sessile drop, hydrostatic weighing, high temperature electrostatic levitation and gamma ray densitometry. Thermal expansion studies on isotropic solids have been reported by several workers using X-ray diffraction [1,2], dilatometry [3,4], FabreyPerot interference method [6] and by other theoretical models [6-13]. Density and Thermal expansion are fundamental thermo physical properties of solids. The study of temperature dependence of these properties is very important in understanding the temperature variation of other properties like elastic constants, refractive indices, dielectric constants, thermal conductivity, diffusion coefficients and other heat transfer dimensionless numbers. Thermal expansion of solids is of technical importance as it determines the thermal stability and thermal shock resistance of the material. In general the thermal expansion characteristics decide the choice of material for the construction of metrological instruments and in the choice of container material in nuclear fuel technology.
Aluminum alloys are very important and extremely useful engineering materials with very good physical properties and finds many applications in modern technology. 7041, 7075 and 7095 aluminum alloys have wide range of applications in aerospace, military and nuclear industry. The gamma radiation attenuation technique for the determination of thermo physical properties in the condensed state offers several advantages over other methods at high temperatures. This is possible because the gamma ray is not in any kind of physical or thermal contact with the material and hence the thermal losses are also reduced and this condition eliminates sample and probe compatibility problem. Using this technique Drotning [14] measured thermal expansion of isotropic solid materials at high temperatures. He studied thermal expansion of Aluminum and type 303 stainless steel at high temperatures and such studies have been extended by him to study the thermal expansion of metals and glasses in the condensed state [14,15]. Recently the gamma radiation attenuation technique has been used to measure the temperature dependence of density of metals [16-19], alloys [20-27] at high temperatures. It is desirable to study the thermophysical properties of new materials at high temperatures for their use in practical applications. There is no study on the temperature variation of thermo physical properties of 7041, 7075 and 7095 aluminum alloys and as such, in the present article, we report the data on the density and thermal expansion of these alloys in the temperature range 300 K to 850 K determined from gamma ray attenuation technique.
2. Theory
The technique of γ-ray attenuation method is based on the fundamental equation
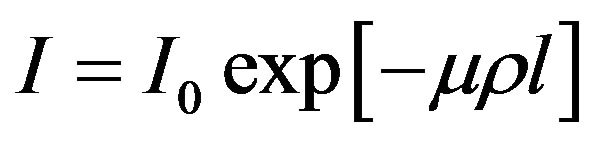 (1)
(1)
where I0, the intensity of γ-ray before passing through the sample, I, the intensity of γ-ray after passing through the sample, µ, the mass attenuation coefficient of the sample, ρ, the density of the sample and l, the thickness of the sample. It is clear from Equation (1) that any change in the temperature of the solid is accompanied by change in it’s density causing a change in the measured intensity. The density and thermal expansion of the materials studied in the present work have been determined following the method suggested by Drotning [28]. The relation between coefficient of volumetric thermal expansion 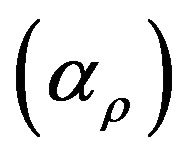 and coefficient of linear thermal expansion
and coefficient of linear thermal expansion  is given by
is given by
 (2)
(2)
where αρ and αl are mean values over a temperature interval. 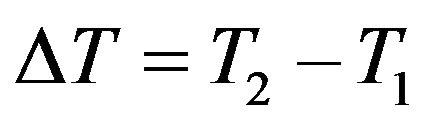 such that
such that

where  etc.
etc.
Rewriting Equation (2) as
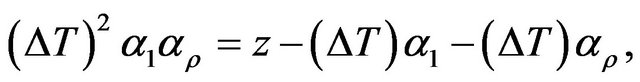 (3)
(3)
where z is defined by
 (4)
(4)
Substituting for αρ from Equation (2) gives
 (5)
(5)
which can be rewritten as
 (6)
(6)
where
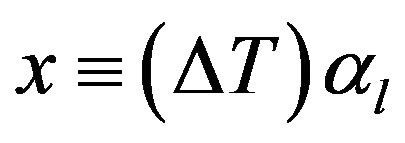 (7)
(7)
The intensities of γ-radiation with sample I and without sample I0 are recorded at every temperature. At room temperature T1, thickness of the sample l1 is measured and using Equation (1) µ is determined. Further measurements of I and I0 at different temperatures enable the determination of z by Equation (4) and hence x can be found from the solution of Equation (6). From the value of x, mean linear thermal expansion (αl) can be determined as a function of temperature.
3. Experimental
Density of a material can be determined by measured attenuation which is produced in a collimated mono energetic beam of gamma radiation. The thermal expansion of the material, change in density for a change in temperature can be determined by gamma ray densitometer. In order to carry out this work, we have designed and fabricated a gamma ray densitometer and a programmable temperature controlled furnace (PTC) which can reach up to a temperature of 1300 K in our laboratory. The experimental set up of gamma ray densitometer in our laboratory is shown in Figure 1. The gamma radiation detector used in our study is a Sodium iodide-thallium activated detector. The 3 inch diameter and 3 inch thick crystal is integrally coupled to a 3 inch diameter photo multiplier tube (PMT). The PMT has a 14 pin base and can be mounted on two types of PMT preamplifier units. The one used in our study is a coaxial in-line pre-amplifier. The detector has a resolution of 8.5% for 137Cs. The alloys studied in the present work were prepared by ingot metallurgy route. The alloys were melted in the air, in the induction furnace and cast iron moulds were used to obtain ingots. These ingots were subsequently homogenized


Figure 1. Gamma ray densitometer set up in our laboratory.
at about 813 K and hot rolled to obtain 0.5 mm - 15 mm thick plates. These alloy plates were precipitation strengthened by heat treatment (aging). The chemical composition of 7041, 7075 and 7095 alloys are given in Table 1. The alloy sample was machined into a perfect cuboid with all the faces finely ground and polished.
The sample was firmly mounted on the flat stainless steel sample holder. The temperature of the sample was measured using a thermocouple sensor. A diffusion pump was then connected to the sample holder tube for evacuation. For inert atmosphere, argon gas was introduced into the quartz tube through the sample holder tube. Then the quartz tube assembly along with the sample was slid into the programmable temperature controlled (PTC) furnace and fixed at appropriate position ensuring a perfect alignment of sample with collimation on either sides. The PTC furnace was programmed in such a way that the furnace temperature is increased by 50 K in every step starting from 300 K above room temperature, and stabilizes there for a certain length of time. Measurement of gamma count rate from a 137Cs through the sample (I) and without sample (Io) were made at a series of equilibrium temperatures and recorded using a multichannel analyzer. Measurement of γ-ray attenuation counts at every step of temperature was repeated a minimum of nine times. The γ-ray counts were recorded while heating and cooling the sample. This procedure was repeated in the temperature range 300 K to 850 K for all the alloy samples.
4. Results and Discussion
The X-ray diffraction (XRD) patterns of these alloys are shown in Figure 2. These XRD patterns confirm that the alloys are in the fcc phase.
The results obtained for the temperature dependence of the linear attenuation coefficient, density and the coefficient of linear thermal expansion of 7041, 7075 and 7095 are summarized in Table 2. All the measurements are confined to solid phase only and the experimental data obtained in the present work have been fit to a linear equation of the form
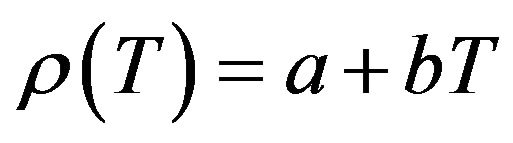 (8)
(8)
Since the measurements have been made in the limited temperature range the coefficient of volumetric thermal expansion (CVTE) of all alloys was calculated using the equation
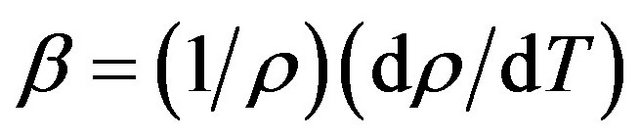 (9)
(9)
Table 1. Chemical composition of 7041, 7075 and 7095.

Table 2. Linear attenuation coefficient, density and the coefficient of linear thermal expansion of 7041, 7075 and 7095 alloys at different temperatures.

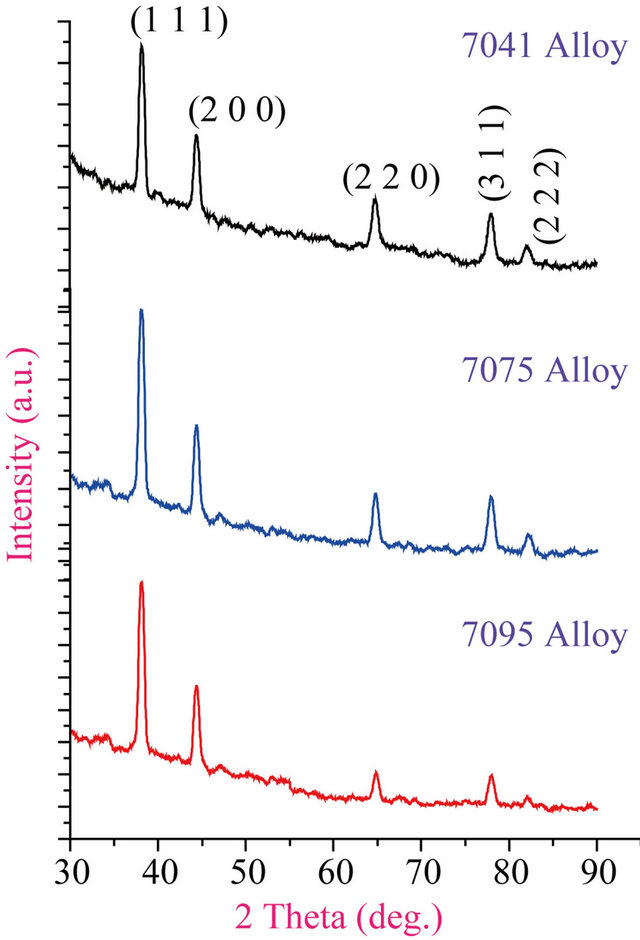
Figure 2. X-ray diffraction patterns of alloys 7041, 7075 and 7095.
where 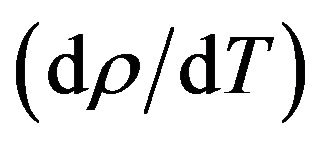 is the first derivative of density with respect to the absolute temperature which is determined from Equation (8). The variation of linear attenuation coefficient with temperature, the temperature dependence of the density and the temperature dependence of linear thermal expansion of 7041, 7075 and 7095 alloys have been shown in Figures 3-5 respectively.
is the first derivative of density with respect to the absolute temperature which is determined from Equation (8). The variation of linear attenuation coefficient with temperature, the temperature dependence of the density and the temperature dependence of linear thermal expansion of 7041, 7075 and 7095 alloys have been shown in Figures 3-5 respectively.
4.1. 7041 Aluminum Alloy
The density of 7041 alloy decreases from a value of 2800 kg∙m−3 at 300 K to a value of 2589 kg∙m−3 at 850 K a decrease of about 7.54%. The temperature dependence is a negative linear function of temperature. For 7041 alloy the temperature dependence of density is represented by linear equation
 (10)
(10)
The coefficient of temperature dependence of density is −0.38364 kg∙m−3∙K−1 and the coefficient of volume thermal expansion is 14 × 10−5 K−1. The thermal expansion increases linearly with temperature and the results on thermal expansion in the temperature range from 300 K to 850 K have been analyzed by least square method and is represented by the linear equation
 (11)
(11)
4.2. 7075 Aluminum Alloy
The density of alloy 7075 at 300 K is 2810 kg∙m−3 its value decreases to a value of 2274 kg∙m−3 at 850 K a decrease of about 19.08% the temperature dependence of

Figure 3. Variation of density of alloy with temperature.
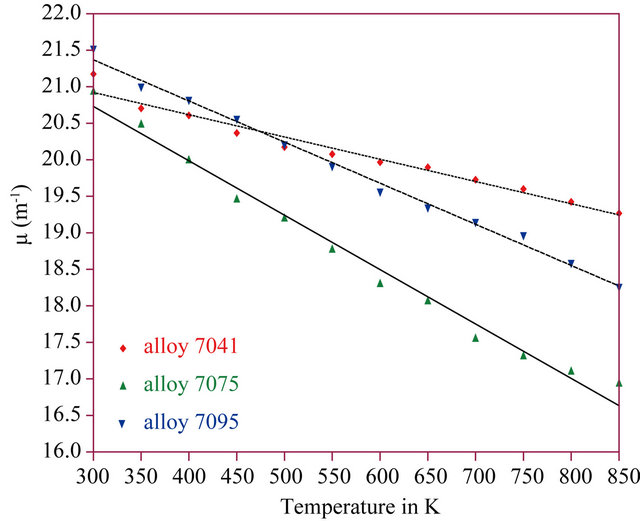
Figure 4. Variation of linear attenuation coefficient with temperature.
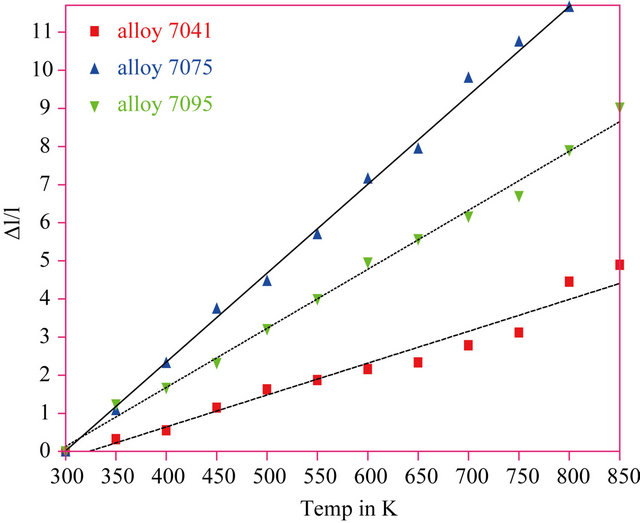
Figure 5. Variation of linear thermal expansion of alloys with temp.
density is a negative linear function of temperature. The temperature dependence of density for 7075 alloy is represented by linear equation
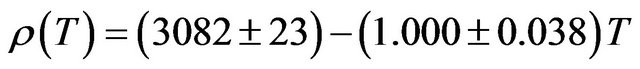 (12)
(12)
The coefficient of temperature dependence of density is −0.9746 kg∙m−3∙K−1 and the coefficient of volume thermal expansion is 35 × 10−5 K−1. The thermal expansion increases linearly with temperature and the results on thermal expansion in the temperature range from 300 K to 850 K have been analyzed and is represented by the linear equation
 (13)
(13)
4.3. 7095 Aluminum Alloy
The density of 7095 alloy decreases from a value of 2890 kg∙m−3 at 300 K to a value of 2452 kg∙m−3 at 850 K, a decrease of about 15.16%. The temperature dependence of density is a negative linear function of temperature. For 7095 alloy the temperature dependence of density is represented by linear equation
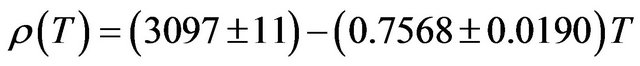 (14)
(14)
The coefficient of temperature dependence of density is −0.7964 kg∙m−3∙K−1 and the coefficient of volume thermal expansion is 28 × 10−5 K−1. The thermal expansion of 7095 alloy increases linearly with temperature and the results on thermal expansion in the temperature range from 300 K to 850 K, have been analyzed and is represented by the linear equation
 (15)
(15)
5. Conclusion
There is no experimental data available on the linear attenuation coefficient as a function of temperature for these alloys. The density and thermal expansion of 7041, 7075 and 7095 aluminum alloys have been reported for the first time. Temperature dependence of density of these alloys does not have anomalous behavior and those values are analyzed with linear equations. The temperature dependence of density shows a negative linear tendency. The linear thermal expansions of these alloys are represented with linear equations.
6. Acknowledgements
The authors thank University Grants Commission (UGC), New Delhi for the financial assistance through Special Assistance Programme (SAP) No. F.530/8/DRS/2009 (SAP-1). Authors also thank the Director, Defense Metallurgical Research Laboratories—DMRL, Hyderabad for providing the facilities for the preparation of alloys.
REFERENCES
- K. K. Srivastava and H. D. Merchant, “Thermal Expansion of Alkali Hallides above 300 K,” Journal of Physics and Chemistry of Solids, Vol. 34, No. 12, 1973, pp. 2069- 2073. doi:10.1016/S0022-3697(73)80055-1
- V. T. Deshpande, “Thermal Expansion of Sodium Flouride and Sodium Bromide,” Acta Crystallographica, Vol. 14, 1961, p. 794. doi:10.1107/S0365110X61002357
- G. K. White, “The Thermal Expansion of Alkali Hallides at Low Temperatures,” Proceedings of the Royal Society London, Vol. A286, No. 1405, 1965, pp. 204-217. doi:10.1098/rspa.1965.0139
- G. K. White and J. G. Collins, “The Thermal Expansion of Alkali Halides at Low Temperatures. II. Sodium, Rubidium and Caesium Halides,” Proceedings of the Royal Society London, Vol. A333, No. 1593, 1973, pp. 237-259. doi:10.1098/rspa.1973.0060
- P. P. M. Meincke and G. M. Graham, “The Thermal Expansion of Alkali Halides,” Canadian Journal of Physics, Vol. 43, No. 10, 1965, pp. 1853-1866.
- A. M. Sherry and M. Kumar, “Analysis of Thermal Expansion for Alkalihalide Crystals Using the Isobaric Equation of State,” Journal of Physics and Chemistry of Solids, Vol. 52, No. 9, 1991, pp. 1145-1148. doi:10.1016/0022-3697(91)90047-4
- M. Kumar and S. P. Upadhyay, “Analysis of the Thermal Expansion Coefficient and It’s Temperature Dependence for Alkali Halides,” Physical Status Solidi, Vol. 181, No. 1, 1994, pp. 55-61.
- K. Wang and R. R. Reeber, “Thermal Expansion of Alkali Halides at High Pressure: NaCl as an Example,” Physics and Chemistry of Minerals, Vol. 23, No. 6, 1996, pp. 254-360. doi:10.1007/BF00199501
- M. Kumar and S. P. Upadhyay, “Pressure Dependence of Thermal Expansivity for Alkali Halides,” Journal of Physics and Chemistry of Solids, Vol. 54, No. 6, 1993, pp. 773-777. doi:10.1016/0022-3697(93)90140-M
- J. F. Vetelino, K. V. Namjoshi and S. S. Mitra, “Mode- Gruneisen Parameters and Thermalexpansion Coefficient of NaCl, CsCl, and Zinc-Blende-Type Crystals,” Journal of Applied Physics, Vol. 1, 1973.
- L. M. Thomas and J. Shanker, “Temperature Dependence of Elastic Constants and Thermal Expansion Coefficient for NaCl Crystals,” Physica Status Solidi, Vol. 195, No. 2, 2006, pp. 361-366.
- Z.-H. Fang, “Temperature Dependence of Inter Atomic Separation for Alkali Halides,” Physica Status Solidi, Vol. 241, No. 13, 2004.
- C. H. Nie, S. Y. Huang and W. Huang, “Temperature Dependence of Anderson Gruneisen Parameter for NaCl,” Applied Physics Research, Vol. 2, No. 1, 2010.
- W. D. Drotning, “Liquid Metals Zinc, Cadmium and Mercury,” Journal of the Less-Common Metals, Vol. 96, 1984, pp. 223-227. doi:10.1016/0022-5088(84)90198-X
- W. D. Drotning, “Thermal Expansion Glasses in the Solid and Liquid Phases,” International Journal of Thermophysics, Vol. 6, No. 6, 1985, pp. 705-714. doi:10.1007/BF00500341
- L. W. Wang, Q. Wang, A. P. Xian and K. Q. Lu, “Precise Measurement of the Densities of Liquid Bi, Sn, Pb and Sb,” Journal of Physics: Condensed Matter, Vol. 15, No. 6, 2003, pp. 777-783. doi:10.1088/0953-8984/15/6/304
- S. V. Stankus, R. A. Khairulin, A. G. Mozgovoy, V. V. Roshchupkin and M. A. Pokrasin, “An Experimental Investigation of the Density of Bismuth in the Condensed State in a Wide Temperature Range,” High Temperature, Vol. 43, No. 3, 2005, pp. 368-378. doi:10.1007/s10740-005-0075-7
- S. V. Stankus and P. V. Tyagel’skii, “Density of High Purity Dysprosium in the Solid and Liquid States,” High Temperature, Vol. 38, No. 4, 2000, pp. 579-583.
- S. V. Stankus, R. A. Khairulin and A. G. Mozgovoy, “Experimental Study of Density and Thermal Expansion of the Advanced Materials and Heat Transfer Agents for Liquid Metal Systems of Thermonuclear Reactor: Lithium,” High Temperature, Vol. 49, No. 2, 2011, pp. 187- 192. doi:10.1134/S0018151X11010214
- S. V. Stankus, R. A. Khairulin and A. G. Mozgovoy, V. V. Roshchupkin and M. A. Pokrasin, “The Density and Thermal Expansion of Eutectic Alloys of Lead with Bismuth and Lithium in Condensed State,” Journal of Physics: Conference Series, Vol. 98, No. 6, 2008, Article ID: 062017. doi:10.1088/1742-6596/98/6/062017
- R. A. Khairulin, S. V. Stankus, R. N. Abdullaev, Yu. A. Plevachuk and K. Yu. Shunyaev, “The Density of the Binary Diffusion Coefficients of Sliver-Tin Melts,” Thermophysics Aeromechanics, Vol. 17, No. 3, 2010, pp. 391- 396.
- R. A. Khairulin and S. V. Stankus, “The Density of Alloys of Tin-Lead System in the Solid and Liquid States,” High Temperature, Vol. 44, 2006, pp. 389-395. doi:10.1007/s10740-006-0048-5
- S. V. Stankus, R. A. Khairulin and A. S. Kosheleva, “Thermal Properties of Liquid Alloys of Magnesium-Lead System,” Thermophysics Aeromechanics, Vol. 14, No. 1, 2007, pp. 75-80.
- T Hupf, C. Cagran, E. Kachnitz and G. Pottlacher, “Thermophysical Properties of Ni80Cr20,” Thermochimica Acta, Vol. 494, No. 1-2, 2009, pp. 40-43. doi:10.1016/j.tca.2009.04.015
- D. E. Burkes, C. A. Papesh, A. P. Maddison, T. Hartmann and F. J. Rice, “Thermo Physical Properties of DU-10 wt% Mo Alloys,” Journal of Nuclear Materials, Vol. 403, No. 1-3, 2010, pp. 160-166.
- S. V. Stankus and R. A. Khairulin, “Density and Phase Diagram of Magnesium-Lead System in the Region of Mg2 Pb Intermetallic Compound,” Thermochimica Acta, Vol. 474, No. 1-2, 2008, pp. 52-56. doi:10.1016/j.tca.2008.05.011
- X. M. Chen, Q. Wang and K. Q. Lu, “Temperature and Time Dependence of Density of Molten Indium Antimonide Measured by Improved Archimedean Method,” Journal of Physics: Condensed Matter, Vol. 11, No. 50, 1999, pp. 10335-10341. doi:10.1088/0953-8984/11/50/325
- W. D. Drotning, “Thermal Expansion of Solid at High Temperature by the Gamma Attenuation Technique,” Review of Scientific Instruments, Vol. 50, No. 12, 1979, pp. 12, Article ID: 121567.

