Journal of Modern Physics
Vol.4 No.2(2013), Article ID:27723,6 pages DOI:10.4236/jmp.2013.42026
Simulation Mechanical Properties of Lead Sulfur Selenium under Pressure
Department of General Science, Faculty of Education, Soran University, Soran-Erbil, Iraq
Email: mazin.sh@soranu.com
Received November 17, 2012; revised December 19, 2012; accepted December 28, 2012
Keywords: PbSSe; Elastic Properties; Pressure
ABSTRACT
The elastic properties of lead sulfur selenium are studied using first-principles calculations. The geometry optimized structural parameters for PbS0.5Se0.5 under different pressures are listed. The lattice parameter increase with increasing pressure, but enthalpy is constant. However, parameter B and Y decrease and parameter S increase with increasing pressure. The elastic constants satisfy the traditional mechanical stability conditions for these ternary mixed crystals. The elastic modulus as two functions of pressure from 0 - 10 GPa are obtained. The calculated elastic constants Cij decrease but with different rates under increasing pressure.
1. Introduction
In both the fundamental physics and high-pressure technique, the study of the mechanical properties of materials is of crucial importance. The determination, by both experimental and theoretical simulations, of the mechanical properties under pressure is a highly challenging task. These properties are closely related to the shear rigidity of materials and correspondingly, to their elastic moduli [1]. The lead salts semiconductors PbS and PbSe have been subject of many experimental and theoretical works. They has been largely used in infrared detectors, as infrared lasers in fiber optics, as thermoelectric materials, in solar energy panels, and in window coatings [2,3]. One of their interesting properties is their narrow fundamental energy band gap [4,5]; that is why, these IV-VI semiconductors are useful in optoelectronic devices such as lasers and detectors [6-8].
There are also many experimental studies for the mixture of these materials, for example, Lebedev and Sluchinskaya have found the appearance of ferroelectricity in these IV-VI semiconductors [9]; and investigated the samples of PbSxSeyTe1−x−y quaternary solid solutions at low temperatures using electrical and X ray methods [10]; ab initio study of cubic PbSxSe1−x alloys by Kacimi et al. [11]; Structure, electronic and optical properties of PbS1-xSex by Labidi et al. [12]; the vacuum evaporated PbS1−xSex thin films were examined by Kumar et al., [13]; and multi-spectral PbSxSe1−x photovoltaic infrared detectors [14] were realized by Schoolar et al.
This study was carried out to shed light on the future studies of scientists who experimentally prepare and test these alloys in laboratories, to help them in determining the change in amounts of additives in alloys, and to determine the accordance of theoretical studies with experiments and other theoretical works. The elastic properties of PbS0.5Se0.5 will change under pressure, which directly influences various applications of PbS-based devices under different working conditions. Taking into account of different application conditions, the elastic properties of lead sulfide at 0 - 10 GPa are studied using first-principles calculations in our work.
2. Computational Method
The first-principles calculations presented here were performed by the CASTEP program on the platform of Materials Studio, which is based on density functional theory using a plane-wave basis set for the expansion of the wave functions [15-17]. Non-local ultra-soft pseudo-potentials were used to describe the valence electrons. Generalized gradient approximation (GGA) with PBE Scheme was adopted to evaluate exchange-correlation energy. Monkhorse-pack mesh was used to select 56 k-points for bulk calculation. A plane-wave cutoff energy of 340 eV was employed throughout. It was shown that the results are well converged at this cutoff. The Pb (5d 6s 6p), S (3s 3p) and Se (3d 4s 4p) were treated as valence state. The geometries for all the systems are optimized. The minimum total energy of the structure is achieved by relaxing the internal coordinates using the Broyden-Fletcher-Goldfarb-Shanno (BFGS) algorithm. The following thresholds for converged structures are employed: energy change per atom <2 × 106 eV, residual force 0.5 eV/nm, stress below 0.05 GPa and the displacement of atoms during the geometry optimization 0.001 nm. The GGA method maybe underestimates the band gap energy in both semiconductors and insulators. We can estimate a multiplicative correction factor to the calculated results in order to adjust the band gap to the experimental results. However, our relative results do not include the correction factor in this paper for convenience.
The elastic constants were calculated by the finite strain method. In this method, the ground state structure is strained according to symmetry-dependent strain patterns with varying amplitudes and a subsequent calculation of the stress tensor after a re-optimization of the internal structure parameters. Further-more, the bulk modulus B and the shear modulus S were calculated from the elastic constants. Young’s modulus was then computed from these values.
3. Results and Discussion
In mechanical properties, element thereof which is acted on by external forces is in a state of stress. Moreover, if the body is in equilibrium, the external stress must be exactly balanced by internal forces. In general, stress is a second rank tensor with nine components as follows [18- 21]:
 (1)
(1)
In an atomistic calculation, the internal stress tensor can be obtained using the so-called virile expression
 (2)
(2)
where index i runs over all particles 1 through N, mi, vi and fi denote the mass, velocity and force acting on particle i, and V0 denotes the (undeformed) system volume.
Application of a stress to a body results in a change in the relative positions of particles within the body, expressed quantitatively via the strain tensor:
 (3)
(3)
For a parallelepiped (e.g., a periodic simulation cell) characterized in some reference state by the three column vectors a0, b0, c0, and by the vectors a, b, c in the deformed state, the strain tensor is given by:
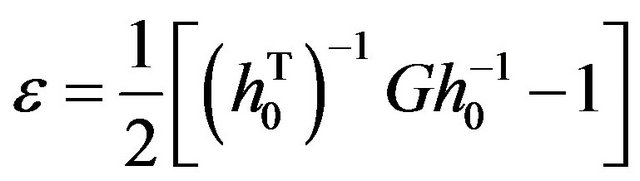 (4)
(4)
where h0 denotes the matrix formed from the three column vectors a0, b0, c0, h denotes the corresponding matrix formed from a, b, c, T denotes the matrix transpose, and G denotes the metric tensor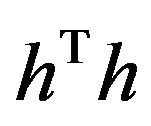 .
.
The elastic stiffness coefficients, relating the various components of stress and strain are defined by:
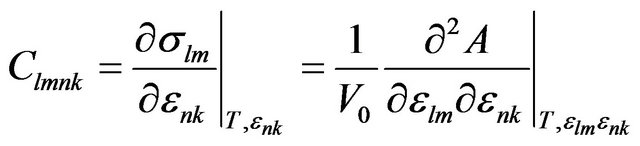 (5)
(5)
where A denotes the Helmholtz free energy.
For small deformations, the relationship between the stresses and strains may be expressed in terms of a generalized Hooke’s law:
 (6)
(6)
or
 (7)
(7)
where Slmnk denote the compliance components. Note that in both Equations (6) and (7), the summation convention is implied. For example, s21 is given in full as:

In view of the fact that both the stress and strain tensors are symmetric, it is often convenient to simplify these expressions by making use of the Voigt vector notation. Stress is represented as:
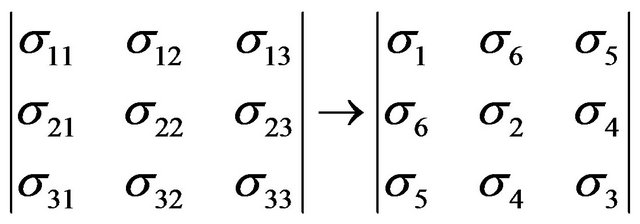 (8)
(8)
For Example
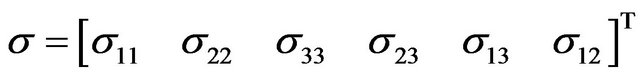
while strain is represented as:
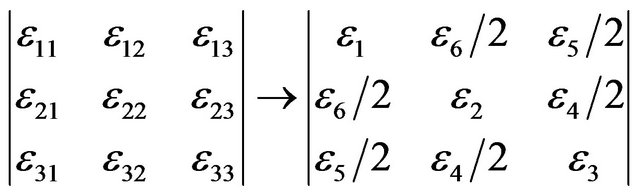 (9)
(9)
For Example: 
The generalized Hooke’s law is thus often written as:
 (10)
(10)
Note that the 6 × 6 stiffness matrix C is also symmetric, and hence a maximum of 21 coefficients is required to fully describe the stress-strain behavior of an arbitrary material. Note also that C is no longer a tensor, since it does not obey the required transformation rules.
For an isotropic material, the stress-strain behavior can be fully described by specifying only two independent coefficients. The resulting stiffness matrix may be written:
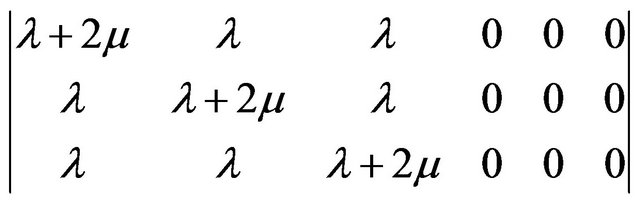 (11)
(11)
where λ and µ are referred to as the Lamé coefficients. For the isotropic case, Expressions used for the Young modulus Y, bulk modulus B and Shear modulus S are given as follows [16,18]:
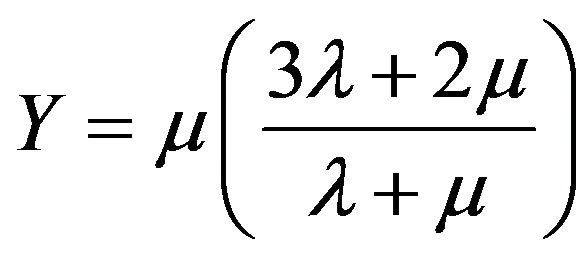 (12)
(12)
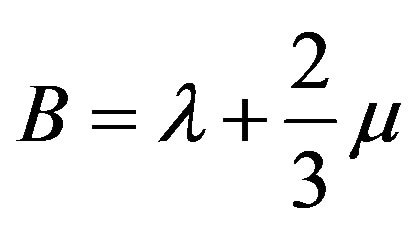 (13)
(13)
 (14)
(14)
As in the first step in calculations, the lattice constants of alloys at equilibrium are calculated by minimizing the lattice parameter of the crystal, i.e. the ratio of total energy of the crystal to its volume. The tested optimization setup convergence is shown in Figure 1 only for Pressure = 5 GPa to save space in journal. The geometry optimized structural parameters for PbS0.5Se0.5 alloys under different pressure are shown in Table 1. Here, E is the enthalpy of the system, B is the bulk modulus, S is the shear modulus and Y is the young’s modulus. These properties, which are the most interesting elastic properties for applications, are often measured for polycrystalline materials when investigating their hardness.
In Table 1, we can find that lattice parameter a and enthalpy E both constant with increasing pressure and S is the increase with increase pressure, However, parameter Y and B decrease with pressure. To our knowledge, many materials usually become metallic with increasing pressure. So, the atoms get closer, lattice parameter decreases, and thus all modulus become larger. But in the PbS0.5Se0.5 alloys lattice parameter increase. So, the atoms get farther and thus modulus becomes larger, these materials become non-metallic with increasing pressure. Figure 2 shows the increase lattice parameters with increasing pressure.
Figure 3 shows elastic modulus of PbS0.5Se0.5 alloys under different pressure, S is the shear modulus, and Y is the Young’s modulus, Parameter Y smaller decrease with pressure and S is the increase with increase pressure. In
Figure 1. The optimization setup convergence of PbS0.5Se0.5 alloys.
Table 1. Geometry optimized structural of PbS0.5Se0.5.
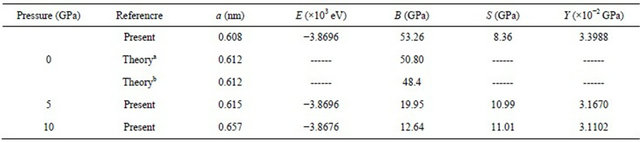
E is the enthapy of the system, Β is bulk modulus, S is the shear modulus and Y is the young’s modulus. Refa. [11], Refb. [12].
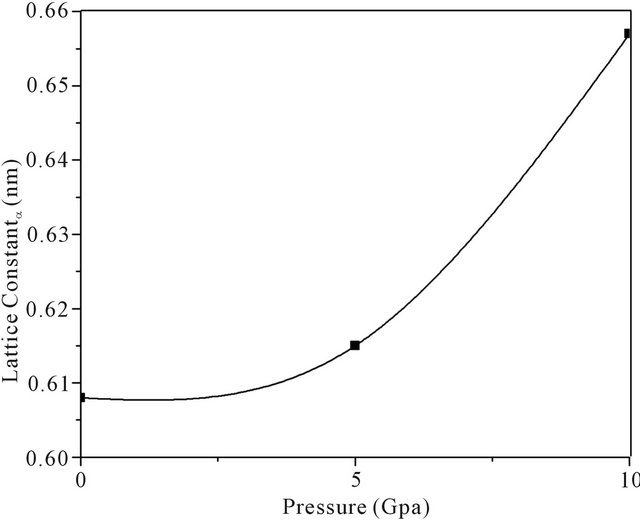
Figure 2. Lattice parameters a of PbS0.5Se0.5 with different pressure.
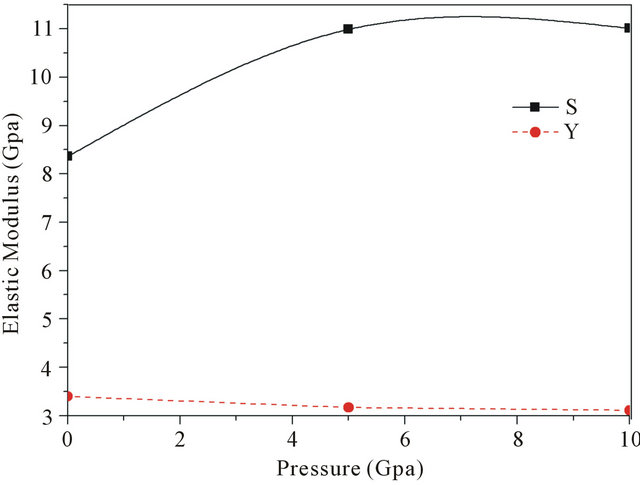
Figure 3. The elastic modulus S and Y versus the pressure.
the present case the bulk modulus B of PbS0.5Se0.5 alloys were studied under different pressure (P = 0.5 and 10 GPa). It is seen that the compressibility, according to the decreasing value of different pressure (see Figure 4).
The elastic constants of solids provide a link between the mechanical and dynamical behavior of crystals, and give important information concerning the nature of the

Figure 4. The compressibility of PbS0.5Se0.5 versus the pressure.
forces operating in solids. In particular, they provide information on the stability and stiffness of materials, and their ab initio calculation requires precise methods. Since the forces and the elastic constants are functions of the first-order and second-order derivatives of the potentials, their calculation will provide a further check on the accuracy of the calculation of forces in solids. The second-order Elastic constants (Cij) are calculated by using the “volume-conserving” technique [22,23] and the findings are given in Table 2.
For a stable tetragonal structure, the six independent elastic constants Cij (C11, C12, C13, C33, C44 and C66) should satisfy the well known Born-Huang criteria for stability [24],
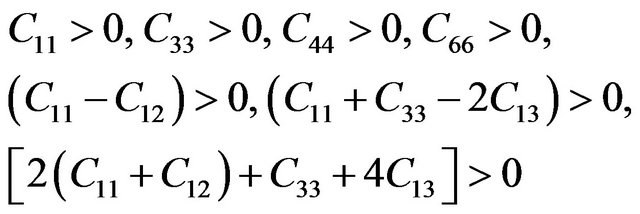
while for cubic crystals, the three independent elastic constants 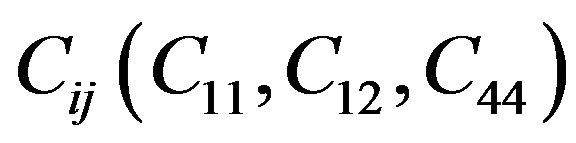 satisfy inequalities,
satisfy inequalities, 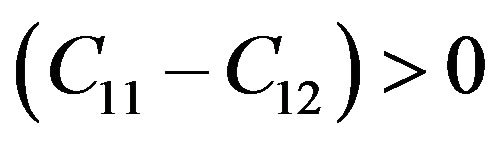 ,
,  ,
, 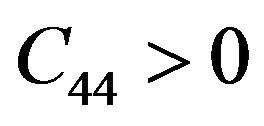 ,
, .
.
Our results for elastic constants in Table 2 obey these stability conditions for PbS0.5Se0.5 alloys.
Table 2. The elastic contants Cij of PbS0.5Se0.5 under different pressure.

The elastic constants Cij are very important for some mechanical properties of PbS0.5Se0.5 especially in some special application conditions such as internal strain and thermo-elastic stress. The calculated results of Cij of PbS0.5Se0.5 as a function of pressure from 0 to 10 GPa are presented in Table 2. For these alloys, no experimental data are available. From this table, we find that C11, C12 and C13 decrease under increasing pressure. However, C33, C44 and C66 decrease but with different rates under increasing pressure.
4. Conclusions
In present work, the elastic properties of lead sulfur selenium are investigated using first-principles calculations. The results are obtained by a first-principles method based on the GGA using plane-wave pseudo potentials. The geometry optimized structural parameters for PbS0.5Se0.5 under different pressures are listed. The elastic constants satisfy the traditional mechanical stability conditions for these ternary mixed crystals. The lattice parameters increase with increasing pressure. However, parameter S is the increase with increase pressure but parameter Y and B decrease with pressure. The calculated results of Cij of PbS0.5Se0.5 as a function of pressure from 0 to 10 GPa are listed. C33, C44 and C66 decrease with different rates under increasing pressure. However C11, C12 and C33 decrease under increasing pressure.
5. Acknowledgements
The authors would like to thank Assistant Researcher Murad Sherzad for some helpful suggestions. This work is supported by Gazi University Research Project under Project No. 05/2008/42.
REFERENCES
- K. S. Badu, C. Vijayan and R. Devanathan, “Strong Quantum Confinement Effects in Polymer-Based PbS Nanostructures Prepared by Ion-Exchange Method,” Materials Letters, Vol. 58, No. 7-8, 2004, pp. 1223-1226. doi:10.1016/j.matlet.2003.09.012
- E. G. See, G. P. Agrawal and N. K. Dutta, “Semiconductors Lazers,” Van Nostrand Reinhold, New York, 1993.
- P. K. Nair, M. Ocampo and A. Fernandez, “Solar Control Characteristics of Chemically Deposited Lead Sulfide Coatings,” Solar Energy Materials, Vol. 20, No. 3, 1990, pp. 235-243. doi:10.1016/0165-1633(90)90008-O
- R. Dalven, H. Ehrenreich, F. Seitz and D. Turnbull, “Electronic Structure of PbS, PbSe, and PbTe,” Solid State Physics, Vol. 28, 1974, pp. 179-224. doi:10.1016/S0081-1947(08)60203-9
- K. Murase, “Anomalous Viscosity in Turbulent Plasma Due to Electromagnetic Instability. II,” Journal of the Physical Society of Japan, Vol. 49, 1980, pp. 725-729. doi:10.1143/JPSJ.49.725
- G. Springholz, V. Holy, M. Pinczolits and G. Bauer, “Self-Organized Growth of Three-Dimensional QuantumDot Crystals with fcc-Like Stacking and a Tunable Lattice Constant,” Science, Vol. 282, No. 5389, 1998, pp. 734-737. doi:10.1126/science.282.5389.734
- H. Zogg, C. Maissen, J. Masek, T. Hoshino, S. Blunier and A. N. Tiwari, “Photovoltaic Infrared Sensor Arrays in Monolithic Lead Chalcogenides on Silicon,” Semiconductor Science and Technology, Vol. 6, No. 12C, 1994, pp. C36-C41. doi:10.1088/0268-1242/6/12C/008
- T. Seetawan and H. Wattanasarn, “First Principle Simulation Mechanical Properties of PbS, PbSe, CdTe and PbTe by Molecular Dynamics,” Procedia Engineering, Vol. 32, 2012, pp. 609-613. doi:10.1016/j.proeng.2012.01.1316
- A. I. Lebedev and I. A. Sluchinskaya, “Ferroelectric Phase Transitions in IV-VI Semiconductors Associated with Off-Center Ions,” Ferroelectrics, Vol. 157, No. 1, 1994, pp. 275-280. doi:10.1080/00150199408229518
- A. I. Lebedev and I. A. Sluchinskaya. “Low-Temperature Phase Transitions in Some Quaternary Solid Solutions of IV-VI Semiconductors,” Journal of Alloys and Compounds, Vol. 203, No. 1, 1994, pp. 51-54. doi:10.1016/0925-8388(94)90713-7
- S. Kacimi, A. Zaoui, B. Abbar and B. Bouhafs, “Ab Initio Study of Cubic PbSxSe1−x Alloys,” Journal of Alloys and Compounds, Vol. 462, No. 1-2, 2008, pp. 135-141. doi:10.1016/j.jallcom.2007.07.068
- M. Labidi, H. Meradji, S. Ghemid and S. Labidi, “Structural, Electronic, Optical and Thermodynamic Properties of PbS, PbSe and Their Ternary Alloy PbS1−xSex,” Modern Physics Letters B, Vol. 25, No. 7, 2011, p. 473. doi:10.1142/S0217984911025729
- S. Kumar, M. A. M. Khan, A. S. Khan and M. Husain, “Studies on Vacuum Evaporated PbS1−xSex Thin Films,” Optical Materials, Vol. 25, No. 1, 2004, pp. 25-32. doi:10.1016/S0925-3467(03)00211-8
- R. B. Schoolar, J. D. Jensen, G. M. Black, S. Foti and A. C. Bouley, “Multispectral PbSxSe1−x and PbySn1−ySe Photovoltaic Infrared Detectors,” Infrared Physics, Vol. 20, No. 4, 1980, pp. 271-275. doi:10.1016/0020-0891(80)90037-8
- P. Hohenberg and W. Kohn, “Inhomogeneous Electron Gas,” Physical Review B, Vol. 136, 1964, pp. B864- B871.
- W. J. Zhao, X. L. Lei, Y. L. Yan, Z. Yang and Y. H. Luo, “The Structural, Electronic and Optical Properties of InxGa1_xP Alloys,” Physica B: Physics of Condensed Matter, Vol. 405, No. 10, 2010, pp. 2357-2361.
- W. Li and J.-F. Chen, “Electronic and Elastic Properties of PbS under Pressure,” Physica B: Condensed Matter, Vol. 405, No. 5, 2010, pp. 1279-1282. doi:10.1016/j.physb.2009.11.067
- M. D. Segall, P. J. D. Lindan, M. J. Probert, C. J. Pickard and P. J. Hasnip, “First-Principles Simulation: Ideas, Illustrations and the CASTEP Code,” Journal of Physics: Condensed Matter, Vol. 14, No. 11, 2002, p. 2717. doi:10.1088/0953-8984/14/11/301
- W. Kohn and L. J. Sham, “Self-Consistent Equations Including Exchange and Correlation Effects,” Physical Review, Vol. 140, No. 4A, 1965, pp. A1133-A1138. doi:10.1103/PhysRev.140.A1133
- M. Othman and E. Kasap, “Ab Initio Investigation of Structural, Electronic and Optical Properties of InxGa1−xAs, GaAs1−yPy Ternary and InxGa1−xAs1−yPy Quaternary Semiconductor Alloys,” Journal of Alloys and Compounds, Vol. 496, No. 1-2, 2010, pp. 226-233. doi:10.1016/j.jallcom.2009.12.109
- B.-T. Liou, C.-Y. Lin, S.-H. Yen and Y.-K. Kuo, “FirstPrinciples Calculation for Bowing Parameter of Wurtzite InxGa1−xN,” Optics Communications, Vol. 249, No. 1-3, 2005, pp. 217-223. doi:10.1016/j.optcom.2005.01.013
- A. D. Milns and D. L. Feucht, “Heterojunctions and Metal-Semiconductor Junctions,” Academic Press, New York and London, 1972.
- N. H. Abrikosov, V. F. Bankina, L. V. Poretskaya, et al., “Semiconductor Compounds, Their Preparation and Properties. Chalcogenides of II, IV and V Group Elements of the Periodic System,” Science, Moscow, 1967.
- B. K. Agrawal and S. Agrawal, “Ab Initio Calculation of the Electronic, Structural, and Dynamical Properties of AlAs and CdTe,” Physical Review B, Vol. 45, No. 15, 1992, pp. 8321-8327. doi:10.1103/PhysRevB.45.8321

