Journal of Modern Physics
Vol.4 No.1(2013), Article ID:26868,5 pages DOI:10.4236/jmp.2013.41006
Wormholes Supported by a Combination of Normal and Quintessential Matter in Einstein and Einstein-Maxwell Gravity
Department of Mathematics, Milwaukee School of Engineering, Milwaukee, USA
Email: kuhfitti@msoe.edu
Received October 27, 2012; revised November 26, 2012; accepted December 4, 2012
Keywords: Wormholes; Quintessential Matter; Einstein-Maxwell Gravity
ABSTRACT
It is shown in the first part of this paper that a combined model comprising ordinary and quintessential matter can support a traversable wormhole in Einstein-Maxwell gravity. Since the solution allows zero tidal forces, the wormhole is suitable for a humanoid traveler. The second part of the paper shows that the electric field can be eliminated (Einstein gravity), but only by tolerating enormous tidal forces. Such a wormhole would still be capable of transmitting signals.
1. Introduction
Traversable wormholes, first conjectured by Morris and Thorne [1], are handles or tunnels in the spacetime topology connecting different regions of our Universe or of different universes altogether. Interest in traversable wormholes has increased in recent years due to an unexpected development, the discovery that our Universe is undergoing an accelerated expansion [2,3]. This acceleration is due to the presence of dark energy, a kind of negative pressure, implying that 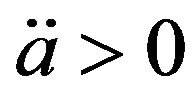 in the Friedmann equation
in the Friedmann equation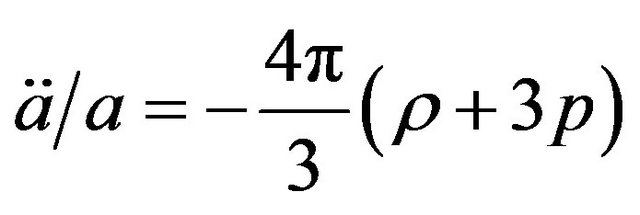 . In the equation of state
. In the equation of state
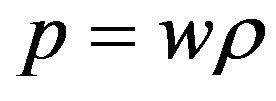 , the range of values
, the range of values  results in
results in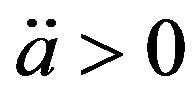 . This range is referred to as quintessence dark energy. Smaller values of
. This range is referred to as quintessence dark energy. Smaller values of 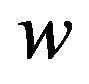 are also of interest. Thus
are also of interest. Thus  corresponds to Einstein’s cosmological constant [4]. The case
corresponds to Einstein’s cosmological constant [4]. The case 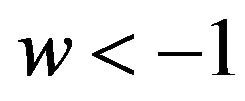 is referred to as phantom energy [5-10]. Here we have
is referred to as phantom energy [5-10]. Here we have , in violation of the null energy condition. As a result, phantom energy could, in principle, support wormholes and thereby cause them to occur naturally.
, in violation of the null energy condition. As a result, phantom energy could, in principle, support wormholes and thereby cause them to occur naturally.
Sections 2-4 discuss a combined model of quintessence matter and ordinary matter that could support a wormhole in Einstein-Maxwell gravity, once again suggesting that such wormholes could occur naturally. The theoretical construction by an advanced civilization is also an inviting prospect since the model allows the assumption of zero tidal forces. Section 4 considers the effect of eliminating the electric field. A wormhole solution can still be obtained but only by introducing a redshift function that results in enormous radial tidal forces, suggesting that some black holes may actually be wormholes fitting the conditions discussed in this paper and so may be capable of transmitting signals, a possibility that can in principle be tested.
2. The Model
Our starting point for a static spherically symmetric wormhole is the line element
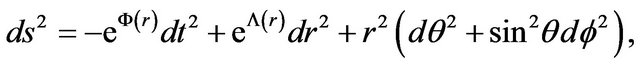 (1)
(1)
where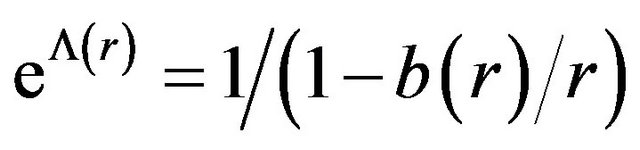 . Here
. Here 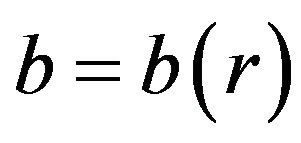 is the shape function and
is the shape function and 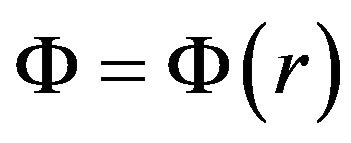 is the redshift function, which must be everywhere finite to prevent an event horizon. For the shape function,
is the redshift function, which must be everywhere finite to prevent an event horizon. For the shape function, 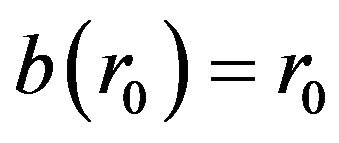 , where
, where 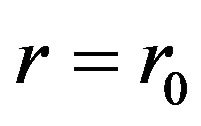 is the radius of the throat of the wormhole. Another requirement is the flare-out condition,
is the radius of the throat of the wormhole. Another requirement is the flare-out condition, 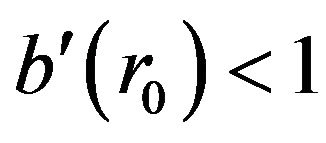 (in conjunction with
(in conjunction with ), since it indicates a violation of the weak energy condition, a primary prerequisite for the existence of wormholes [1].
), since it indicates a violation of the weak energy condition, a primary prerequisite for the existence of wormholes [1].
In this paper the model proposed for supporting the wormhole consists of a quintessence field and a second field with (possibly) anisotropic pressure representing normal matter. Here the Einstein field equations take on the following form (assuming ):
):
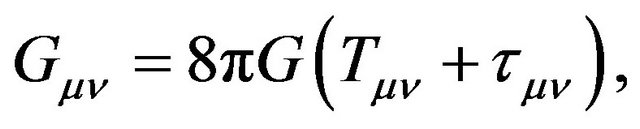 (2)
(2)
where 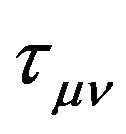 is the energy momentum tensor of the quintessence-like field, which is characterized by a free parameter
is the energy momentum tensor of the quintessence-like field, which is characterized by a free parameter 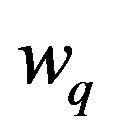 such that
such that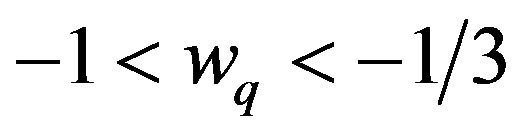 . Following Kiselev [11], the components of this tensor satisfy the following conditions:
. Following Kiselev [11], the components of this tensor satisfy the following conditions:
 (3)
(3)
 (4)
(4)
Furthermore, the most general energy momentum tensor compatible with spherically symmetry is
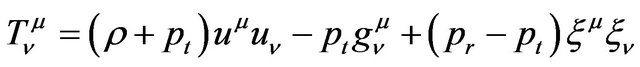 (5)
(5)
with . The Einstein-Maxwell field equations for the above metric corresponding to a field consisting of a combined model comprising ordinary and quintessential matter are stated next [12,13]. Here
. The Einstein-Maxwell field equations for the above metric corresponding to a field consisting of a combined model comprising ordinary and quintessential matter are stated next [12,13]. Here 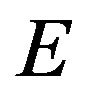 is the electric field strength,
is the electric field strength,  the electric charge density, and
the electric charge density, and  the electric charge.
the electric charge.
 (6)
(6)
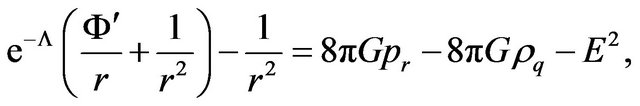 (7)
(7)
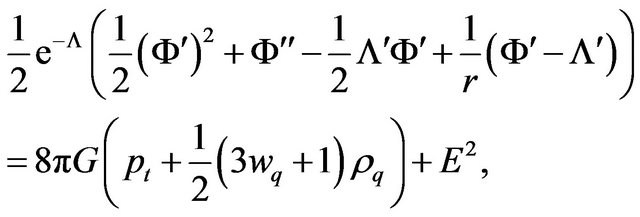 (8)
(8)
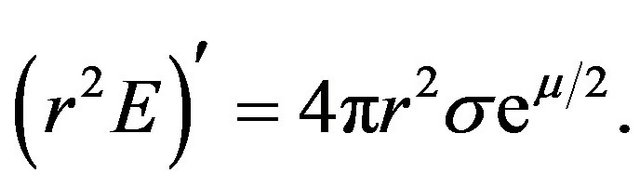 (9)
(9)
Equation (9) can also be expressed in the form
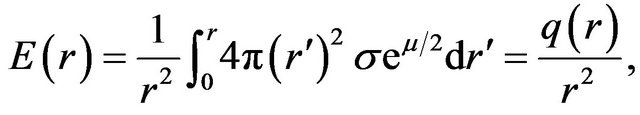 (10)
(10)
where  is the total charge on the sphere of radius
is the total charge on the sphere of radius .
.
3. Solutions
We assume that for the normal-matter field we have the following equation of state for the radial pressure [14]:
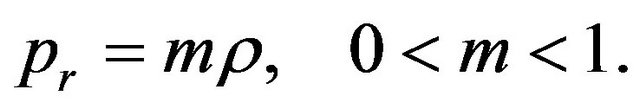 (11)
(11)
For the lateral pressure we assume the equation of state
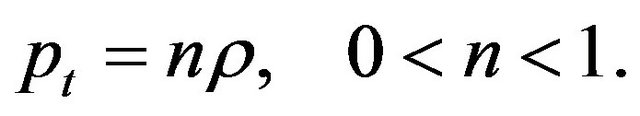 (12)
(12)
Generally,  is not equal to
is not equal to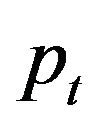 , unless, of course,
, unless, of course,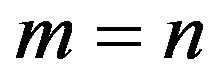 .
.
Following Ref. [14], the factor 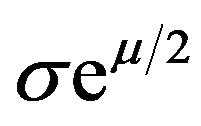 is assumed to have the form
is assumed to have the form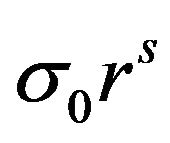 , where
, where 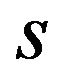 is an arbitrary constant and
is an arbitrary constant and 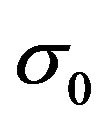 is the charge density at
is the charge density at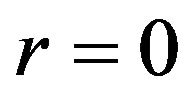 . As a result,
. As a result,
 (13)
(13)
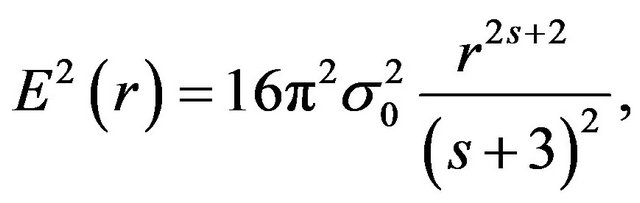 (14)
(14)
and
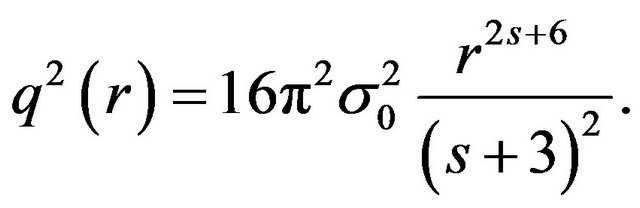 (15)
(15)
The next step is to obtain the shape function 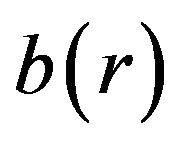 by deriving a differential equation that can be solved for
by deriving a differential equation that can be solved for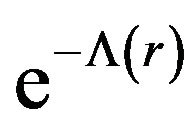 . The easiest way to accomplish this is to solve Equation (6) for
. The easiest way to accomplish this is to solve Equation (6) for 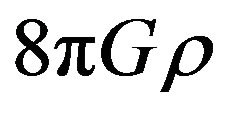 and substituting the resulting expression in Equation (7), which, in turn, is solved for
and substituting the resulting expression in Equation (7), which, in turn, is solved for . After substituting this expression in Equation (8) and making use of Equations (11) and (12), we obtain the simplified form
. After substituting this expression in Equation (8) and making use of Equations (11) and (12), we obtain the simplified form
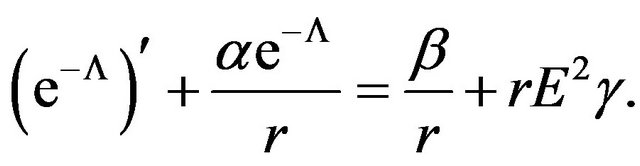 (16)
(16)
Here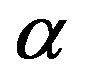 ,
,  , and
, and  are dimensionless quantities given by the following:
are dimensionless quantities given by the following:
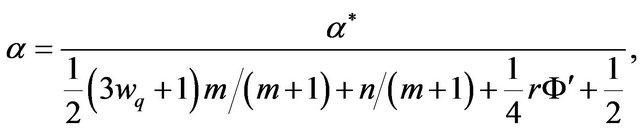 (17)
(17)
where
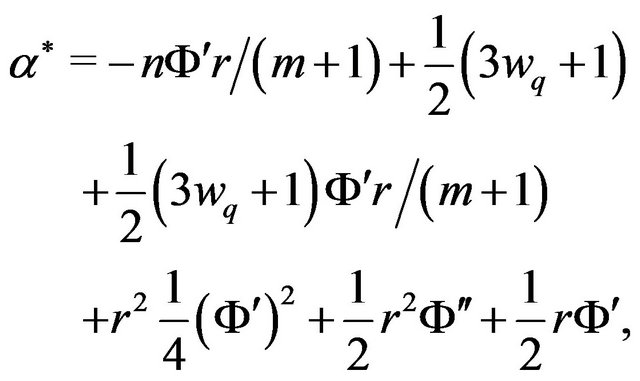
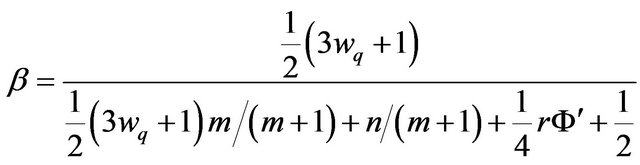 (18)
(18)
and
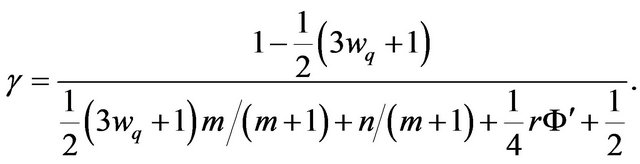 (19)
(19)
Equation (16) is linear and would readily yield an exact solution provided that 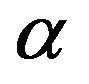 and
and  are constants. This can only happen if
are constants. This can only happen if  for some constant
for some constant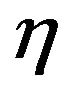 . In the first part of this paper we will assume that
. In the first part of this paper we will assume that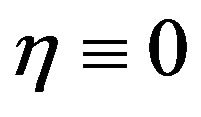 , leading to the zero-tidal-force solution [1]. Whether occurring naturally or constructed by an advanced civilization, such a wormhole would be suitable for humanoid travelers.
, leading to the zero-tidal-force solution [1]. Whether occurring naturally or constructed by an advanced civilization, such a wormhole would be suitable for humanoid travelers.
Returning to Equation (16) and using Equation (14), the integrating factor  yields the solution
yields the solution
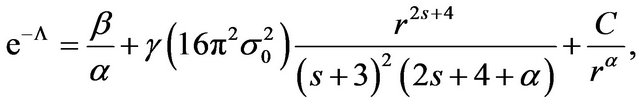 (20)
(20)
where  is an integration constant. From
is an integration constant. From  in Section 2, we obtain the shape function
in Section 2, we obtain the shape function
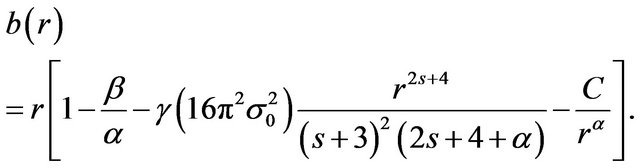 (21)
(21)
4. Wormhole Structure
In Equation (20), 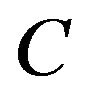 is an integration constant. So mathematically,
is an integration constant. So mathematically, 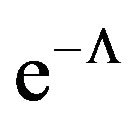 is a solution for every
is a solution for every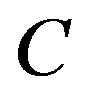 , leading to
, leading to 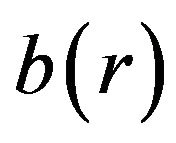 in Equation (21). Physically, however,
in Equation (21). Physically, however, 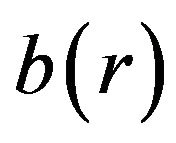 is going to satisfy the requirements of a shape function only for a range of values of
is going to satisfy the requirements of a shape function only for a range of values of . This problem can best be approached graphically by assigning some typical values to the various parameters and adjusting the value of
. This problem can best be approached graphically by assigning some typical values to the various parameters and adjusting the value of , as exemplified by Figure 1. First observe that if
, as exemplified by Figure 1. First observe that if , then
, then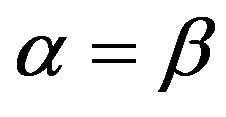 . For the given values
. For the given values ,
, 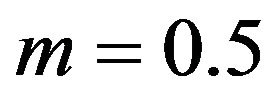 ,
, 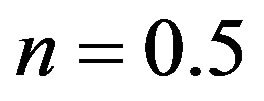 ,
, 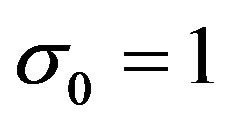 , and
, and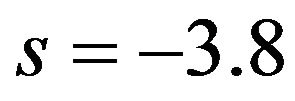 , a suitable value for
, a suitable value for 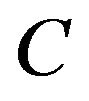 is
is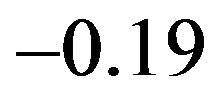 , as we will see. Substituting in Equation (21), we obtain
, as we will see. Substituting in Equation (21), we obtain
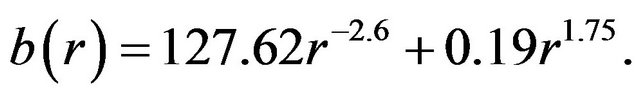 (22)
(22)
To locate the throat  of the wormhole, we define the function
of the wormhole, we define the function 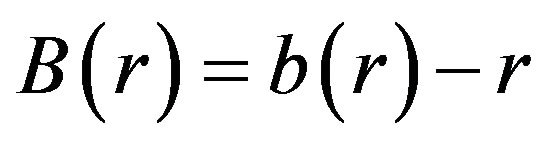 and determine where
and determine where 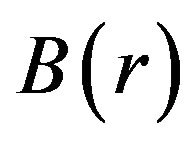 intersects the
intersects the 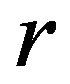 -axis, as shown in Figure 2. Observe that Figure 2 indicates that for
-axis, as shown in Figure 2. Observe that Figure 2 indicates that for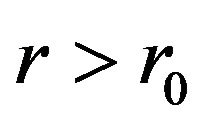 ,
, 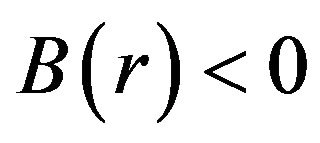 , so that
, so that 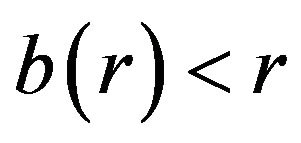 for
for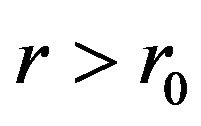 , an essential requirement for a shape function. Furthermore,
, an essential requirement for a shape function. Furthermore, 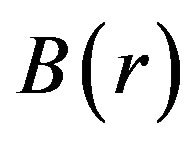 is a decreasing function near
is a decreasing function near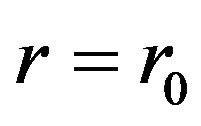 ; so
; so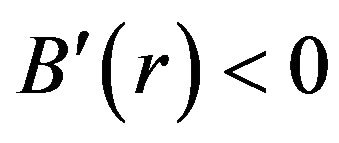 , which implies that
, which implies that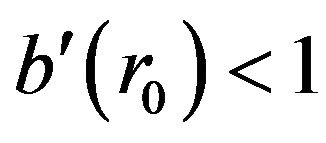 , the flare-out condition. With the flare-out condition now satisfied, the shape function has produced the desired wormhole structure. For completeness let us
, the flare-out condition. With the flare-out condition now satisfied, the shape function has produced the desired wormhole structure. For completeness let us
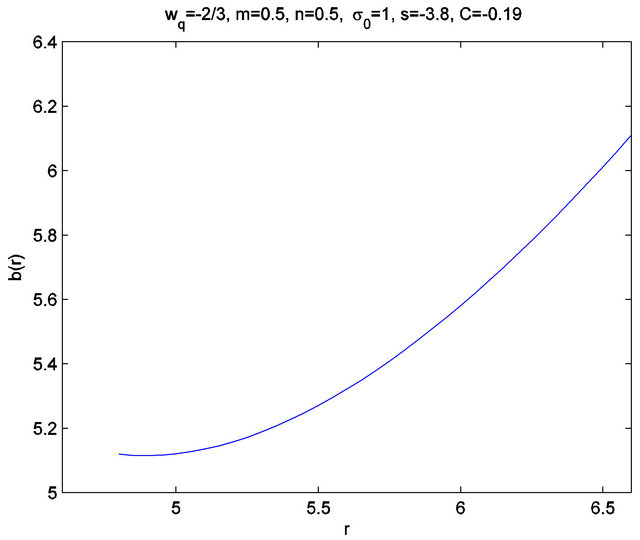
Figure 1. The shape function.
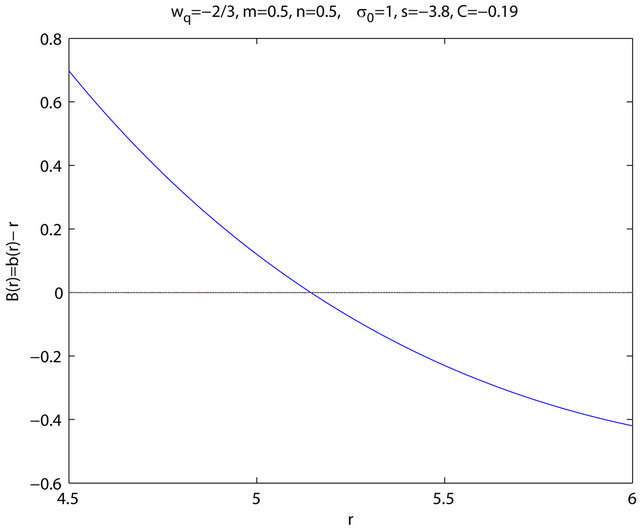
Figure 2.  intersects the
intersects the  -axis at
-axis at .
.
note that 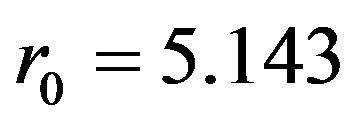 and
and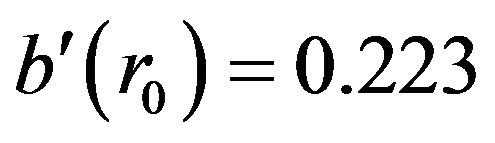 . (Suitable choices for
. (Suitable choices for  corresponding to other parameters will be discussed at the end of the section).
corresponding to other parameters will be discussed at the end of the section).
To the right of ,
,  keeps rising, but at
keeps rising, but at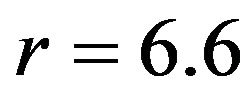 ,
, 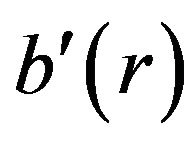 is still less than unity. So at
is still less than unity. So at , the interior shape function, Equation (22), can be joined smoothly to the exterior function
, the interior shape function, Equation (22), can be joined smoothly to the exterior function
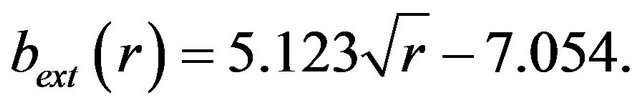
To check this statement, observe that
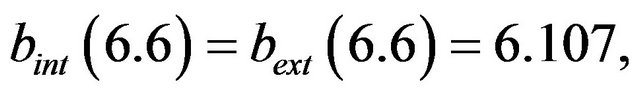
while
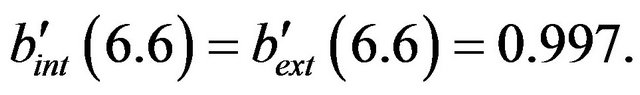
To the right of ,
, 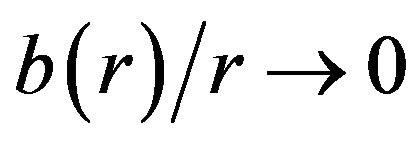 as
as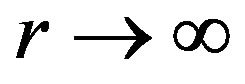 , so that after adjusting the constant redshift function, the wormhole spacetime is asymptotically flat. (The components
, so that after adjusting the constant redshift function, the wormhole spacetime is asymptotically flat. (The components  and
and 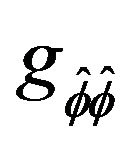 are already continuous for the exterior and interior components, respectively [15-17]).
are already continuous for the exterior and interior components, respectively [15-17]).
Returning to Equation (21), an example of an anisotropic case is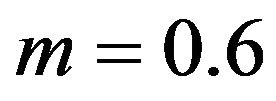 ,
,  ,
, 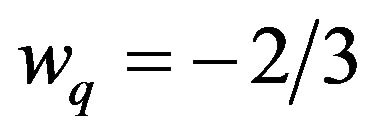 ,
, 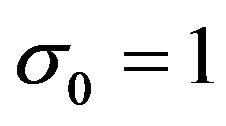 , and
, and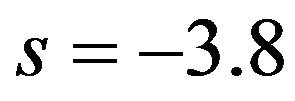 ; a suitable choice for
; a suitable choice for  is
is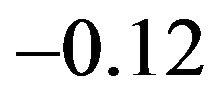 . The result is
. The result is

Here  and
and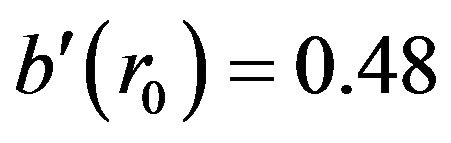 .
.
An example of a value of 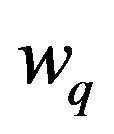 closer to −1, the lower end of the quintessence range, is the following:
closer to −1, the lower end of the quintessence range, is the following: ,
, 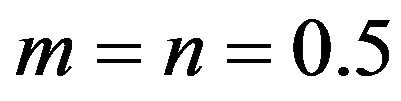 ,
, 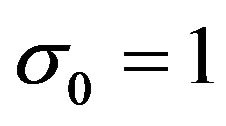 , and
, and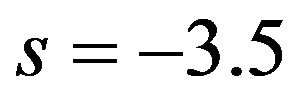 . Letting
. Letting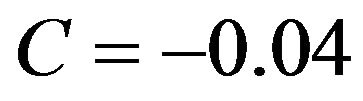 , the shape function is
, the shape function is
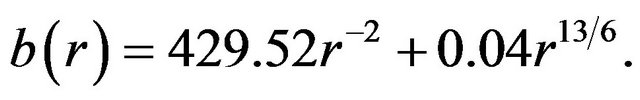
This time 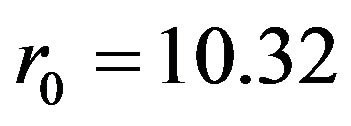 and
and .
.
5. Could the Electric Field Be Eliminated?
The purpose of this section is to study conditions under which a combined model of quintessential and ordinary matter may be sufficient without the electric field .
.
If  is eliminated, then the assumption of zero tidal forces becomes too restrictive. So we assume that
is eliminated, then the assumption of zero tidal forces becomes too restrictive. So we assume that  for some nonzero constant
for some nonzero constant . This, in turn, means that
. This, in turn, means that
 (23)
(23)
Now Equation (16) yields
 (24)
(24)
Both 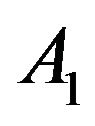 and
and 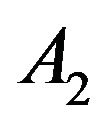 are positive integration constants. (The reason that
are positive integration constants. (The reason that  has to be positive is that
has to be positive is that  is close to zero whenever
is close to zero whenever 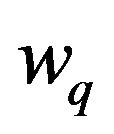 is close to
is close to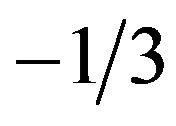 );
);  and
and  now become (for
now become (for )
)
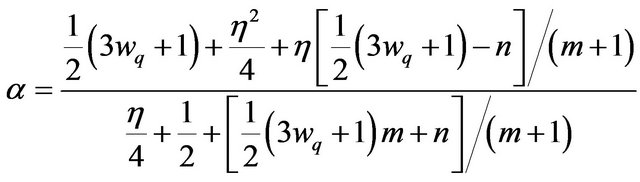 (25)
(25)
and
 (26)
(26)
The last two equations are similar to those in Ref. [12], which deals with galactic rotation curves.
As noted in Section 2, the shape function  is obtained from
is obtained from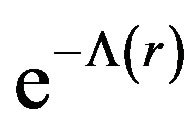 , so that
, so that
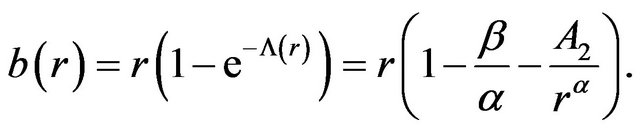 (27)
(27)
To meet the condition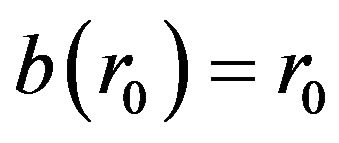 , we must have
, we must have
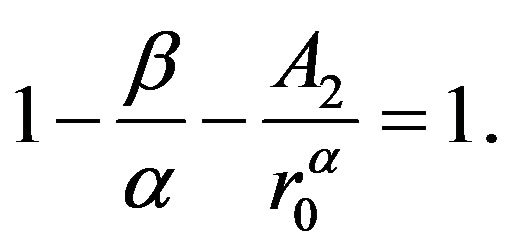
Solving for , we obtain the radius of the throat:
, we obtain the radius of the throat:
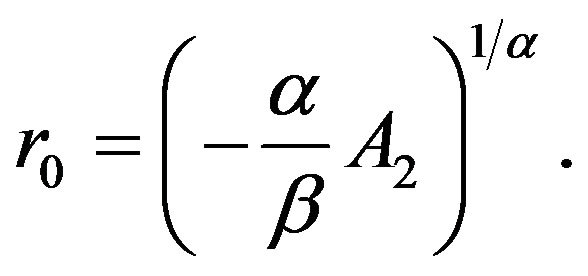 (28)
(28)
Since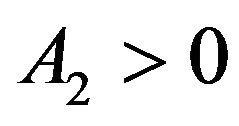 ,
,  and
and  must have opposite signs. From
must have opposite signs. From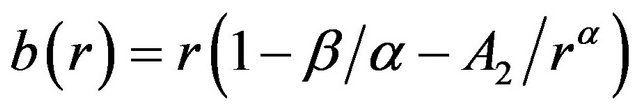 , we have
, we have
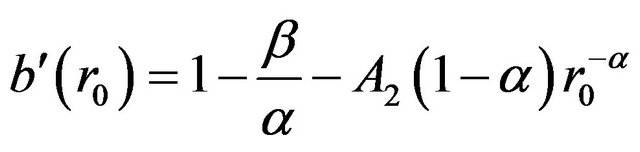
and, after substituting Equation (28),

which simplifies to . It follows immediately that if
. It follows immediately that if , then
, then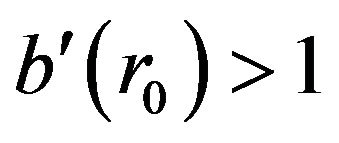 , so that the flare-out condition cannot be met. To get a value for
, so that the flare-out condition cannot be met. To get a value for  between 0 and 1, the exponent
between 0 and 1, the exponent 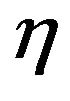 in the redshift function, Equation (23), has to be negative and sufficiently large in absolute value. Such a value will cause
in the redshift function, Equation (23), has to be negative and sufficiently large in absolute value. Such a value will cause  to be negative, which can best be seen from a simple numerical example: for convenience, let us choose
to be negative, which can best be seen from a simple numerical example: for convenience, let us choose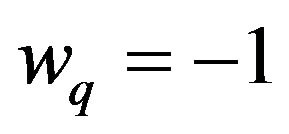 , the lower end of the quintessence range, and
, the lower end of the quintessence range, and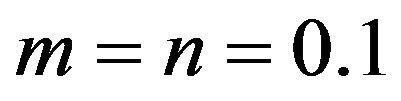 . Then we must have
. Then we must have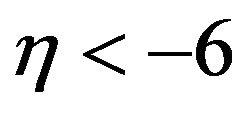 . The result is a large positive numerator in Equation (25) because the last term is positive and
. The result is a large positive numerator in Equation (25) because the last term is positive and 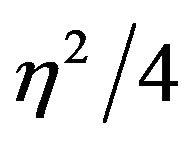 is large. So
is large. So 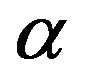 and
and  have opposite signs, as expected. (Observe that for the isotropic case, if
have opposite signs, as expected. (Observe that for the isotropic case, if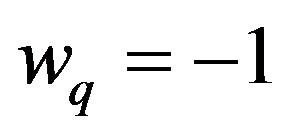 , then the values of
, then the values of 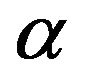 and
and  are independent of
are independent of 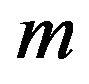 and
and ).
).
Continuing the numerical example, if we let 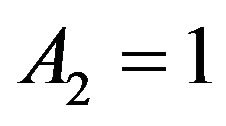 and
and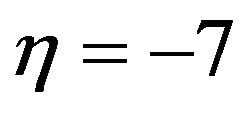 , then
, then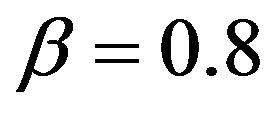 ,
, 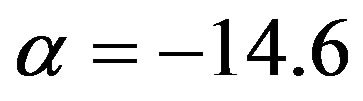 , and
, and
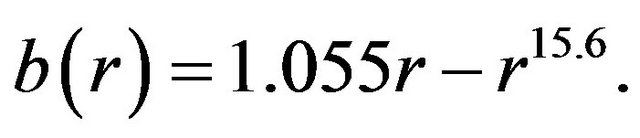
From Equation (28), 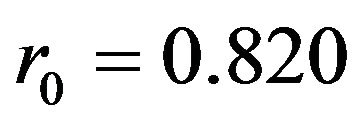 , while
, while
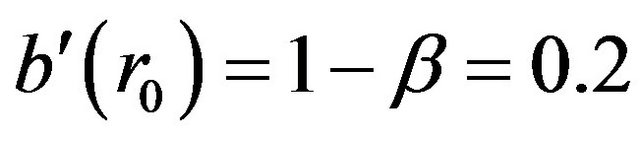 .
.
As we have seen,  is independent of
is independent of . So we are free to choose a smaller value in Equation (28) to obtain a larger throat size.
. So we are free to choose a smaller value in Equation (28) to obtain a larger throat size.
We conclude that we can readily find an interior wormhole solution around 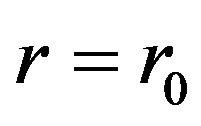 without
without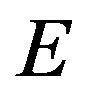 , provided that we are willing to choose a sufficiently large (and negative) value for
, provided that we are willing to choose a sufficiently large (and negative) value for , resulting in what may be called an unpalatable shape function:
, resulting in what may be called an unpalatable shape function: . At the throat,
. At the throat,  , which indicates the presence of an enormous radial tidal force, even for large throat sizes. (Recall that from Ref. [1], to meet the tidal constraint, we must have roughly
, which indicates the presence of an enormous radial tidal force, even for large throat sizes. (Recall that from Ref. [1], to meet the tidal constraint, we must have roughly . Such a wormhole would not be suitable for a humanoid traveler, but it may still be useful for sending probes or for transmitting signals.
. Such a wormhole would not be suitable for a humanoid traveler, but it may still be useful for sending probes or for transmitting signals.
The enormous tidal force is actually comparable to that of a solar-mass black hole of radius 2.9 km near the event horizon, making the solution physically plausible: since we have complete control over 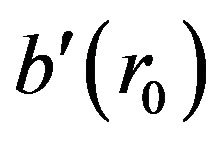 and
and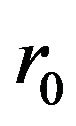 , we are not only able to satisfy the flare-out condition but we can place the throat wherever we wish. Moreover, the assumption
, we are not only able to satisfy the flare-out condition but we can place the throat wherever we wish. Moreover, the assumption  is equivalent to Einstein’s cosmological constant, the best model for dark energy [18]. Also physically desirable is the assumption of isotropic pressure, i.e.,
is equivalent to Einstein’s cosmological constant, the best model for dark energy [18]. Also physically desirable is the assumption of isotropic pressure, i.e., 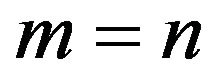 in the respective equations of state. As we have seen, in the isotropic case our conclusions are independent of
in the respective equations of state. As we have seen, in the isotropic case our conclusions are independent of  and
and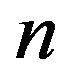 . So by placing the throat just outside the event horizon of a suitable black hole, it is possible in principle to construct a “transmission station” for transmitting signals to a distant advanced civilization and, conversely, receiving them. If such a wormhole were to exist, it would be indistinguishable from a black hole at a distance. This suggests a possibility in the opposite direction: A black hole could conceivably be a wormhole fitting our description. The easiest way to test this hypothesis is to listen for signals, artificial or natural, emanating from a (presumptive) black hole.
. So by placing the throat just outside the event horizon of a suitable black hole, it is possible in principle to construct a “transmission station” for transmitting signals to a distant advanced civilization and, conversely, receiving them. If such a wormhole were to exist, it would be indistinguishable from a black hole at a distance. This suggests a possibility in the opposite direction: A black hole could conceivably be a wormhole fitting our description. The easiest way to test this hypothesis is to listen for signals, artificial or natural, emanating from a (presumptive) black hole.
6. Conclusions
This paper discusses a class of wormholes supported by a combined model consisting of quintessential matter and ordinary matter, first in Einstein-Maxwell gravity and then in Einstein gravity, that is, in the absence of an electric field. To obtain an exact solution, it was necessary to assume that the redshift function has the form 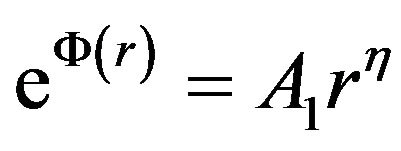 for some constant
for some constant . In the Einstein-Maxwell case, this constant could be taken as zero, thereby producing a zero-tidal-force solution, which, in turn, would make the wormhole traversable for humanoid travelers. Without the electric field
. In the Einstein-Maxwell case, this constant could be taken as zero, thereby producing a zero-tidal-force solution, which, in turn, would make the wormhole traversable for humanoid travelers. Without the electric field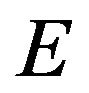 , the exponent
, the exponent 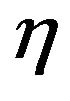 has to be nonzero and leads to a less desirable solution with large tidal forces. Concerning the exact solution, it is shown in Ref. [19] that the existence of an exact solution implies the existence of a large set of additional solutions, suggesting that wormholes of the type discussed in this paper could occur naturally.
has to be nonzero and leads to a less desirable solution with large tidal forces. Concerning the exact solution, it is shown in Ref. [19] that the existence of an exact solution implies the existence of a large set of additional solutions, suggesting that wormholes of the type discussed in this paper could occur naturally.
It is argued briefly in the Einstein case with a quintessential-dark-energy background that some black holes may actually be wormholes with enormous tidal forces, a hypothesis that may be testable.
REFERENCES
- M. S. Morris and K. S. Thorne, “Wormholes in Spacetime and Their Use for Interstellar Travel: A Tool for Teaching General Relativity,” American Journal of Physics, Vol. 56, No. 5, 1988, pp. 395-412. doi:10.1119/1.15620
- A. G. Riess, et al., “Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant,” Astronomical Journal, Vol. 116, No. 3, 1998, pp. 1009-1038. doi:10.1086/300499
- S. J. Perlmutter, et al., “Measurements of Ω and Λ from 42 High-Redshift Supernovae,” Astrophysical Journal, Vol. 517, No. 2, 1999, pp. 565-586. doi:10.1086/307221
- M. Carmeli, arXiv: astro-ph/0111259, 22 p.
- S. V. Sushkov, “Wormholes Supported by a Phantom Energy,” Physical Review D, Vol. 71, No. 4, 2005, Article ID: 043520.
- O. B. Zaslavskii, “Exactly Solvable Model of a Wormhole Supported by Phantom Energy,” Physical Review D, Vol. 72, No. 6, 2005, Article ID: 061303.
- F. S. N. Lobo, “Phantom Energy Traversable Wormholes,” Physical Review D, Vol. 71, No. 8, 2005, Article ID: 084011.
- P. K. F. Kuhfittig, “Seeking Exactly Solvable Models of Traversable Wormholes Supported by Phantom Energy,” Classical and Quantum Gravity, Vol. 23, No. 20, 2006, pp. 5853-5860. doi:10.1088/0264-9381/23/20/007
- F. Rahaman, M. Kalam, M. Sarkar and K. Gayen, “A Theoretical Construction of Wormhole Supported by Phantom Energy,” Physics Letters B, Vol. 633, No. 2-3, 2006, pp. 161-163. doi:10.1016/j.physletb.2005.11.080
- P. K. F. Kuhfittig, F. Rahaman and A. Ghosh, “Quintom Wormholes,” International Journal of Theoretical Physics, Vol. 49, No. 6, 2010, pp. 1222-1231. doi:10.1007/s10773-010-0302-9
- V. V. Kiselev, “Quintessence and Black Holes,” Classical and Quantum Gravity, Vol. 20, No. 6, 2003, pp. 1187- 1197. doi:10.1088/0264-9381/20/6/310
- F. Rahaman, P. K. F. Kuhfittig, K. Chakraborty, M. Kalam and D. Hossain, “Modeling Galactic Halos with Predominantly Quintessential Matter,” International Journal of Theoretical Physics, Vol. 50, No. 9, 2011, pp. 2655- 2665. doi:10.1007/s10773-011-0761-7
- A. A. Usmani, F. Rahaman, S. Ray, K. K. Nandi, P. K. F. Kuhfittig, Sk. A. Rakib and Z. Hasan, “Charged Gravastars Admitting Conformal Motion,” Physics Letters B, Vol. 701, No. 4, 2011, pp. 388-392. doi:10.1016/j.physletb.2011.06.001
- F. Rahaman, M. Kalam and K.A. Rahman, “Wormhole Geometry from Real Feasible Matter Sources,” International Journal of Theoretical Physics, Vol. 48, No. 2, 2009, pp. 471-475. doi:10.1007/s10773-008-9822-y
- J. P. S. Lemos, F. S. N. Lobo and S. Q. de Oliveira, “Morris-Thorne Wormholes with a Cosmological Constant,” Physical Review D, Vol. 68, No. 6, 2003, Artical ID: 064004.
- J. P. S. Lemos and F. S. N. Lobo, “Plane Symmetric Traversable Wormholes in an Anti-de Sitter Background,” Physical Review D, Vol. 69, No. 10, 2004, Article ID: 104007.
- P. K. F. Kuhfittig, “A Single Model of Traversable Wormholes Suppported by Generalized Phantom Energy or Chaplygin Gas,” General Relativity and Gravitation, Vol. 41, No. 7, 2009, pp. 1485-1496. doi:10.1007/s10714-008-0716-3
- R. Bousso, “The Cosmological Constant,” General Relativity and Gravitation, Vol. 40, No. 2-3, 2008, pp. 607- 637. doi:10.1007/s10714-007-0557-5
- P. K. F. Kuhfittig, “Some Remarks on Exact Wormhole Solutions,” Advanced Studies in Theoretical Physics, Vol. 5, No. 8, 2011, pp. 365-370.

