Journal of Modern Physics
Vol.3 No.9A(2012), Article ID:23058,10 pages DOI:10.4236/jmp.2012.329149
Phase-Space Areas of the Body Motion in the Solar System Deduced from the Bohr-Sommerfeld Atomic Theory and Approximate Invariance of Their Ratios for the Pairs of Planets and Satellites
Institute of Physical Chemistry, Polish Academy of Science, Warsaw, Poland
Email: solszewski@ichf.edu.pl
Received July 5, 2012; revised August 4, 2012; accepted August 11, 2012
Keywords: Ratios of the Phase-Space Areas and Their Invariance; Planets and Satellites; Bohr-Sommerfeld Atomic Theory
ABSTRACT
Energy-time and momentum-position phase spaces defined by the electron orbits in the hydrogen-like atom exhibit special properties of equivalence. It is demonstrated that equivalence of the same kind can be obtained for the phase-space areas defined by the orbit pairs of planets, or satellites, which compose the solar system. In the choice of the examined areas it is useful to be guided by the Bohr-Sommerfeld atomic theory.
1. Introduction
In physics, but not only in this domain, we look very often for parameters which allow us to identify the examined objects. For example a typical parameter of this kind is the mass which helps us to identify a given particle, or a system of particles collected together, say, in an atom. Also large systems of particles, especially those composed of mainly the same atoms or molecules, have some properties which are characteristic for the whole ensemble. A typical parameter is here a definite temperature associated—at special conditions—with the change of the system phase, for example the change is from a vapour to a liquid. Sometimes a combination of several parameters is required to be characteristic for a system.
In mechanics of a circular motion of a body along a specific closed orbit there are important phase integrals
 (1)
(1)
met in the Sommerfeld quantum conditions; see e.g. [1]. Here p is the body momentum and q is the body position on the orbit. The integral (1) is the phase-space area of the variables 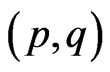 circumvented by the body in course of its motion along the orbit. The body energy E—which is conserved on the orbit—can be represented as a function of S and the frequency
circumvented by the body in course of its motion along the orbit. The body energy E—which is conserved on the orbit—can be represented as a function of S and the frequency 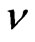 of the body motion, equal to the reciprocal value of the circulation period T, becomes
of the body motion, equal to the reciprocal value of the circulation period T, becomes
 (2)
(2)
In some special cases, however, for example for a linear oscillator, there is a linear dependence between E and S, so 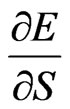 is a constant independent of E or the amplitude of oscillation. In this case we have
is a constant independent of E or the amplitude of oscillation. In this case we have
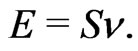 (3)
(3)
A characteristic property of (3) is that the ratio
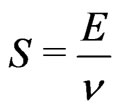 (4)
(4)
called the adiabatic invariant, remains unchanged for slow changes of the oscillator Hamiltonian [2].
But in case of the body orbital motion in the solar system the simplifications of (3) and (4) do not hold. For from the reversed Formula (2) we obtain (see e.g. [3]):
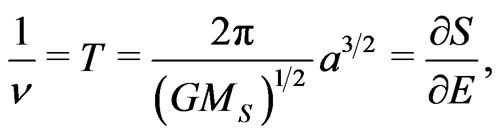 (5)
(5)
where G is the gravitational constant, a—the major semiaxis of the Kepler orbit and 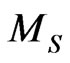 is the central mass which for the planetary orbital motion is the mass of the Sun. Since
is the central mass which for the planetary orbital motion is the mass of the Sun. Since
 (6)
(6)
where 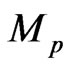 is the planetary mass, we obtain
is the planetary mass, we obtain
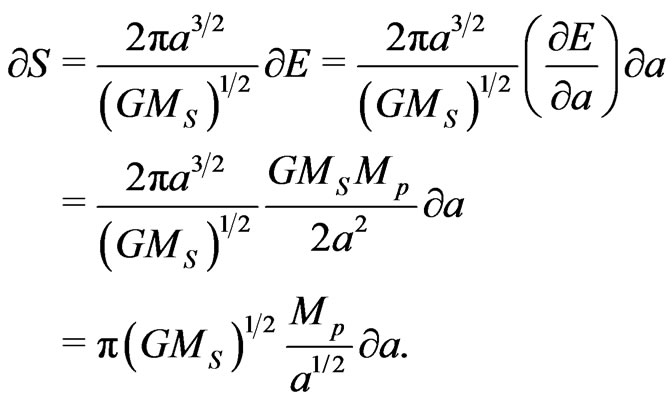 (7)
(7)
The integration performed for (7) gives, with the accuracy to a constant term,
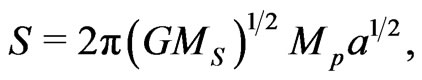 (8)
(8)
whereas the product of 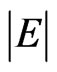 and T becomes
and T becomes
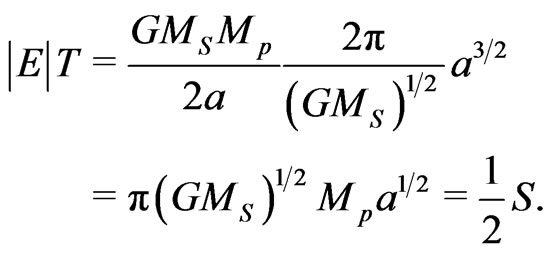 (9)
(9)
But a similar relation can be obtained for the product of the planetary momentum P and average distant R of the moving body from the Sun, if we note that for the Kepler motion of planets the eccentricity parameter e is regularly small, so
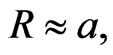 (10)
(10)
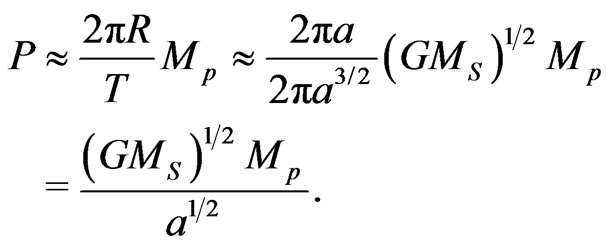 (11)
(11)
In this case
 (12)
(12)
therefore
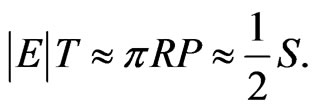 (13)
(13)
Evidently, the products entering (13) together with S in (8) represent the phase-space areas of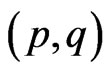 .
.
However, any of the factors E, T, R, and P entering (13) depends on a in a different way, and a separate dependence on a applies to S. A question which may arise here is as follows: if we have a pair of the planetary objects in which one of the objects has its
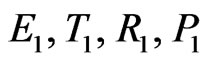 (14)
(14)
at some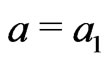 , and
, and , and the other object in this pair has its
, and the other object in this pair has its
 (15)
(15)
at some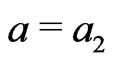 , and
, and , is it possible to combine the phase-space areas obtained in terms of parameters entering (14) and (15) in such a way that the resulted combination is approximately independent of
, is it possible to combine the phase-space areas obtained in terms of parameters entering (14) and (15) in such a way that the resulted combination is approximately independent of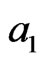 ,
,  ,
,  , and
, and ? In effect, such a combination may become approximately constant for the whole of the planetary system.
? In effect, such a combination may become approximately constant for the whole of the planetary system.
We find an affirmative answer to that question, also for the satellitary systems, and details of the corresponding formulae are given below. It should be noted, however, that a search for the required formalism is much facilitated when similarities which exist in description of the Kepler’s planetary problem and the electron motion in the framework of the Bohr-Sommerfeld atomic theory are taken into account.
2. Parameters Useful in Calculating the Phase-Space Areas of the Planetary Motion
Similarities between the planetary motion performed in the gravitational field of the Sun and the electron motion in the electrostatic field of the atomic nucleus are well known. However, any quantitative reference between parameters characteristic for both kinds of the examined motions is rather difficult to assess. This difficulty seems, in general, to be quite obvious if we note a macroscopic nature of the planetary objects and microscopic properties of an atom. Nevertheless, a geometric and mechanical similarity in the behaviour of the solar system to that of an atomic system considered in the framework of the old quantum theory is evident. This similarity may suggest a quantitative search for comparison between the macroworld of planets and the microworld connected with the electron motion in an atom. A search of this kind can materialize in definite calculations when the properties of the phase space associated with an electron circulating in the atom are compared with the phase space of the planetary, or satellitary, motion in the solar system.
In practice, the position-momentum and energy-time phase spaces can be defined both for the orbiting planets and the circulating electron. Here, for the sake of simplicity, the elliptical character of orbits can be approximately neglected equally in the macroscopic and the microscopic case. Let us begin with the action function Sn for a planet on the orbit n which satisfies the relation
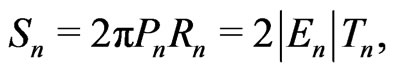 (16)
(16)
whereas a similar action function for an electron moving on a circular trajectory corresponding to the atomic state 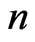 is
is
 (17)
(17)
Symbols Pn, Rn, En and Tn in (16) denote respectively the momentum, orbital radius
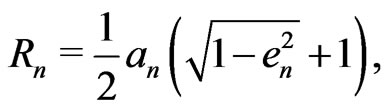 (18)
(18)
energy and time period on the planetary orbit  having the major semiaxis
having the major semiaxis 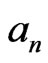 and the eccentricity
and the eccentricity 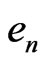 [4-6], whereas
[4-6], whereas ,
,  ,
,  and
and 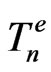 in (17) are similar parameters for an electron in its quantum state, or on an orbit, labelled also by
in (17) are similar parameters for an electron in its quantum state, or on an orbit, labelled also by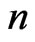 . In our calculations we are guided by the atomic properties which are given by the formulae [7]:
. In our calculations we are guided by the atomic properties which are given by the formulae [7]:
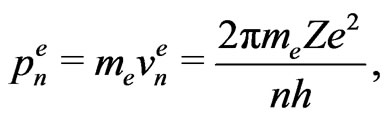 (19)
(19)
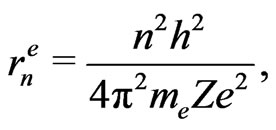 (20)
(20)
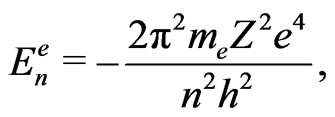 (21)
(21)
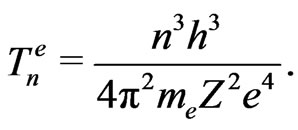 (22)
(22)
Here Ze is the nucleus charge,  the electron charge,
the electron charge, 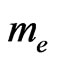 the electron mass, and h is the Planck constant.
the electron mass, and h is the Planck constant.
3. Change of the Phase-Space Area Due to the Orbit Change
When the orbit n is changed to another orbit, say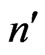 , the parts of the difference in the action function equal to
, the parts of the difference in the action function equal to
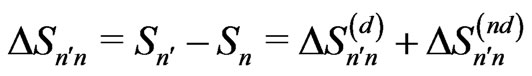 (23)
(23)
can be examined both in the planetary and the electron case. These parts can be classified as diagonal (d) changes represented by the formulae
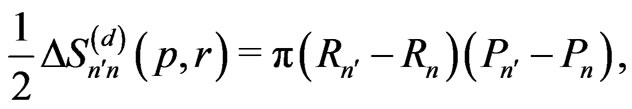 (24)
(24)
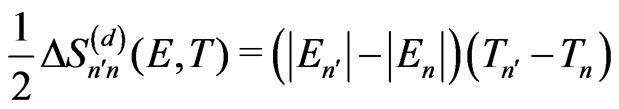 (25)
(25)
concerning respectively the momentum-position and energy-time phase-space areas entering Sn and 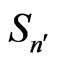 in (16). Similar non-diagonal
in (16). Similar non-diagonal 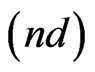 changes entering
changes entering  are
are
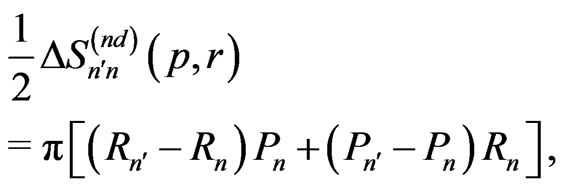 (26)
(26)
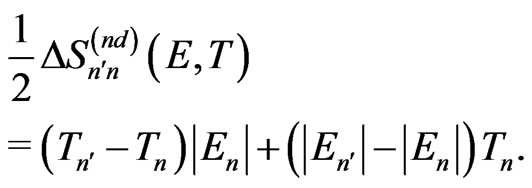 (27)
(27)
In the next step, it can be noted that relations concerning components of 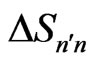 for planets defined in (24)- (27) can be calculated also for the changes
for planets defined in (24)- (27) can be calculated also for the changes 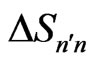 for electrons, on condition Pn, Rn, En and Tn entering the mentioned formulae are replaced by
for electrons, on condition Pn, Rn, En and Tn entering the mentioned formulae are replaced by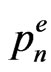 ,
,  ,
, 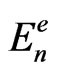 and
and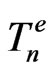 . The electron parameters give [6]:
. The electron parameters give [6]:
 (28)
(28)
 (29)
(29)
for small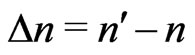 , so the ratio
, so the ratio
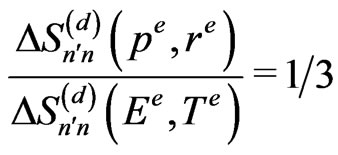 (30)
(30)
is practically a constant number independent of the orbit index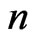 . In a further step
. In a further step
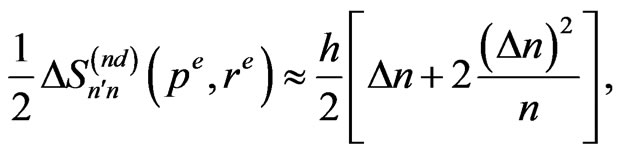 (31)
(31)
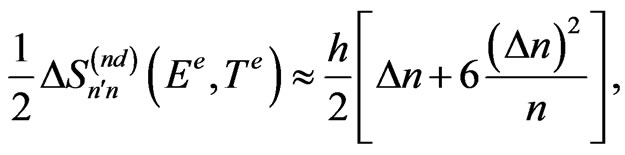 (32)
(32)
so the ratio of (31) and (32) is approximately also a constant:
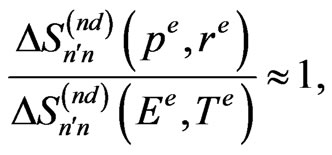 (33)
(33)
which holds especially on condition when .
.
A check of the properties of (30) and (33) for the solar system has been done on the numerical way; see [6]. An almost constant behaviour of (30) is widely confirmed, although this ratio becomes close rather to unity, especially for planets, than to 1/3 obtained in (30). On the other hand, the ratio (33) fluctuates more than (30) for different planetary, or satellitary, pairs chosen to occupy n and . This behaviour can be attributed to unequal second terms entering the square brackets in (31) and (32). In the most part of the examined planetary cases the ratio between (31) and (32) is about 2 instead of the result approximately equal to 1 obtained in (33).
. This behaviour can be attributed to unequal second terms entering the square brackets in (31) and (32). In the most part of the examined planetary cases the ratio between (31) and (32) is about 2 instead of the result approximately equal to 1 obtained in (33).
4. Phase-Space Areas Made Free from the Orbit Index and Their Comparison
A more convenient way of comparison between the phase-space areas for an electron moving in the atom and similar areas obtained for circulating planets is when these areas are made, at least approximately, free from the orbital index. This situation, in fact, can be obtained beginning with the areas for the moving electron. For example, such an area in the momentum-position space about state 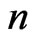 can be defined as
can be defined as
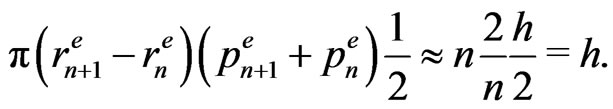 (34)
(34)
The result in (34) holds on condition  is assumed to be a large number. The area in (34) is a belt of thickness
is assumed to be a large number. The area in (34) is a belt of thickness
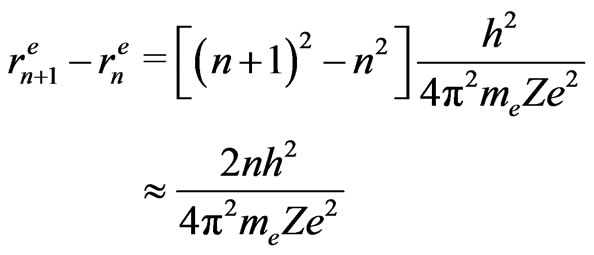 (35)
(35)
plotted in the coordinate space, and the length of the belt is proportional to
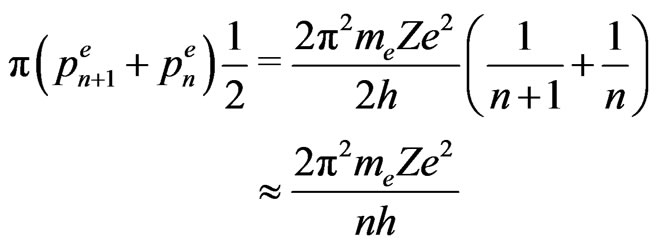 (36)
(36)
in the momentum space. A similar area can be defined when the roles of 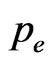 and
and  are reversed. In this case we obtain the phase-space area equal to
are reversed. In this case we obtain the phase-space area equal to
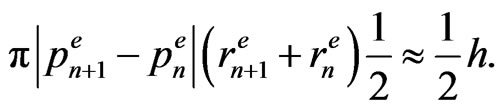 (37)
(37)
Here the thickness of the belt is
 (38)
(38)
and the belt length is proportional to
 (39)
(39)
The results obtained in (34) and (37) are: 1) close to ; 2) they differ only by a factor of 2.
; 2) they differ only by a factor of 2.
A similar evaluation can be done for the phase space areas composed of the electron energies and the time periods of the rotational motion about the nucleus; see (21) and (22). We obtain for one electron state the areas
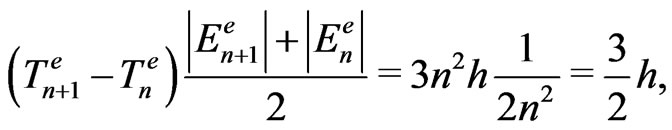 (40)
(40)
 (41)
(41)
because for a large n we find:
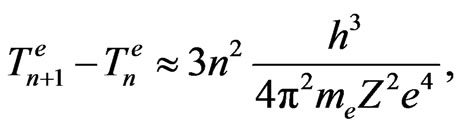 (42)
(42)
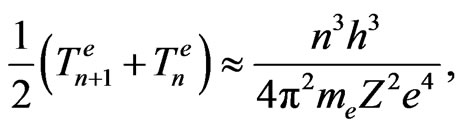 (43)
(43)
 (44)
(44)
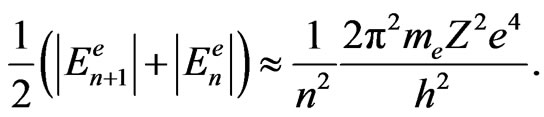 (45)
(45)
The areas calculated in (40) and (41) are: 1) close to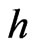 ; 2) differ only by a factor of
; 2) differ only by a factor of . Evidently, the area (40) is a kind of the belt having its length extended in the energy space and the belt thickness is in the period-oftime space, whereas (41) represents the belt of reversed shape properties.
. Evidently, the area (40) is a kind of the belt having its length extended in the energy space and the belt thickness is in the period-oftime space, whereas (41) represents the belt of reversed shape properties.
Because of a similar character of the electron motion in the Bohr-Sommerfeld atom and the planetary motion in the solar system, we expect similar phase-space properties for both kinds of the motion. An essential difference is here that the electron has the same mass on any orbit , but this does not apply to the planetary orbits. Therefore a more realistic comparison should concern the case when momenta expressions entering the examined areas are replaced by velocities, and—consequently—the energies of the moving bodies are divided by the orbiting mass. For electrons we obtain on any orbit n
, but this does not apply to the planetary orbits. Therefore a more realistic comparison should concern the case when momenta expressions entering the examined areas are replaced by velocities, and—consequently—the energies of the moving bodies are divided by the orbiting mass. For electrons we obtain on any orbit n
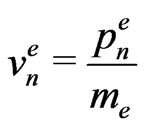 (46)
(46)
for the velocity, and
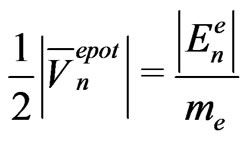 (47)
(47)
for the reduced energy. Because of the virial theorem, the expression (47) is equal to a half of the absolute average value of the potential acting on a moving electron. In effect of the substitutions (46) and (47) we obtain the following belt areas for the electron case:
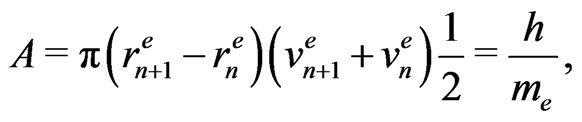 (19a)
(19a)
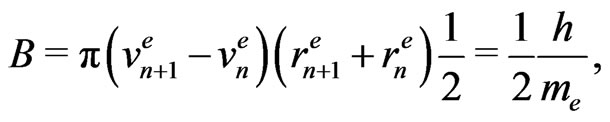 (22a)
(22a)
 (25a)
(25a)
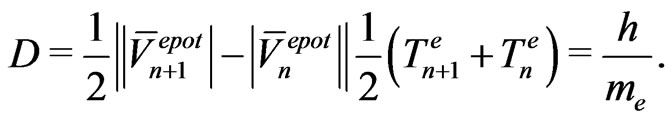 (26a)
(26a)
Section 5 examines similar expressions calculated for the planetary and satellitary orbits.
5. Belt Areas in the Phase-Space Calculated for Planets and Satellites
In the first step let us examine the equivalence of the belt areas in the position-momentum space and areas in the energy-time period space without the mass reduction for the body momentum and energy performed below [see (56) and (57)]. In this case we have
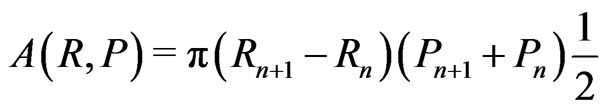 (48)
(48)
similar to (19a),
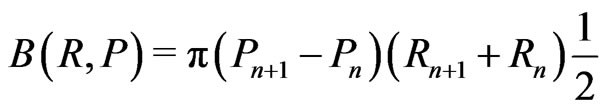 (49)
(49)
similar to (22a),
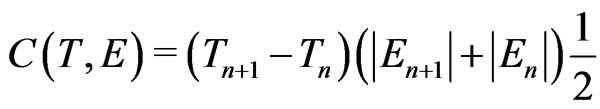 (50)
(50)
similar to (25a), and
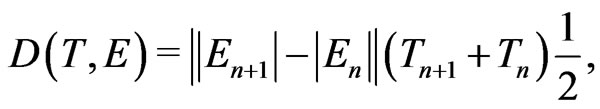 (51)
(51)
similar to (26a) calculated for an electron in the BohrSommerfeld atom. The factor of 1/2 entering the formulae (48)-(51) provides us with the arithmetical mean of the corresponding parameters defining the belt lengths. The belt areas (48)-(51) are calculated in Tables 1 and 2 together with the ratios 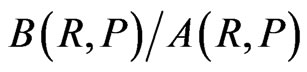 and
and 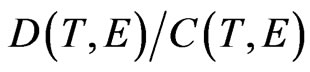 which roughly satisfy the relations:
which roughly satisfy the relations:
 (52)
(52)
The input data in Tables 1 and 2 are taken from [5,6] and Table 3. For the same planetary and satellitary pairs another ratio equal to

Table 1. Belt areas between the neighbouring planet orbits calculated (in Js) for the momentum-position and energy-time phase spaces and their ratios; for A(R,P) and B(R,P) see Equations. (48) and (49); for C(T,E) and D(T,E) see, respectively, (50) and (51). The entering data are based on [5,6].

Table 2. Belt areas between the neighbouring satellite orbits calculated (in Js) for the momentum-position and energy-time phase spaces and their ratios; for the symbols meaning see (48)-(51). The entering data are based on [5,6] and Table 3.

Table 3. Corrected data for one of the satellites of Saturn and two satelites of Uranus; see [5] and [6]. The period Tn is given in sidereal days (1 sidereal day = 86400 s); Rn is the mean distance of the satellite from planet center (in 103 m); Msn is the satellite mass (in kg); En is the satellite energy (in J); Pn is the satellite momentum (in kg·ms–1).
 (53)
(53)
is calculated in Table 4.
In the next step, we examine the relations between the phase-space areas when the mass reduction of the body momentum and energy mentioned at the end of Section 4 is done.
The planetary mass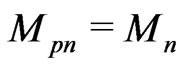 , or the satellite mass
, or the satellite mass  enter both sides of Equation (16). The reduction of this mass gives instead of (16):
enter both sides of Equation (16). The reduction of this mass gives instead of (16):
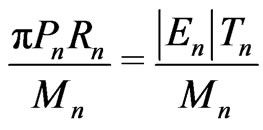 (54)
(54)
or
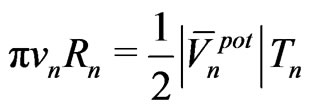 (55)
(55)
where
 (56)
(56)
is the velocity of a circulating celestial body and
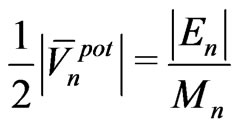 (57)
(57)
is the absolute value of the average potential of that body.
This is so because 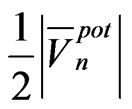 in (57) multiplied by
in (57) multiplied by  and differentiated with respect to the distance
and differentiated with respect to the distance  equals to a half of the gravitational force acting between the motion center and the orbiting body.
equals to a half of the gravitational force acting between the motion center and the orbiting body.
A substitution of (56) and (57) instead of  and
and 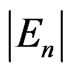 entering (48)-(53) [see a similar operation done for the atomic case in (46), (47) and the formulae (19a), (22a), (25a) and (26a)] gives:
entering (48)-(53) [see a similar operation done for the atomic case in (46), (47) and the formulae (19a), (22a), (25a) and (26a)] gives:
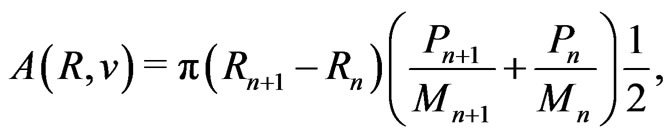 (58)
(58)
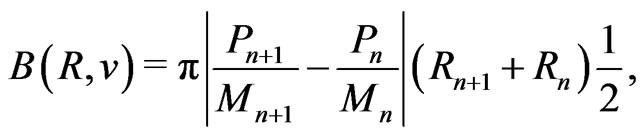 (59)
(59)
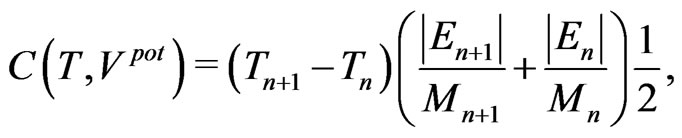 (60)
(60)
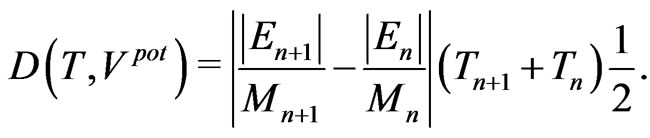 (61)
(61)
Expressions
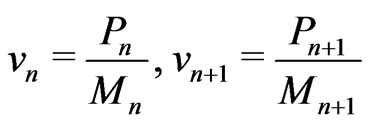 (62)
(62)
are the velocities of the bodies on the orbits n and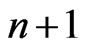 , whereas
, whereas
 (63)
(63)
represent the average body potentials on these orbits.
The ratios obtained for the hydrogen-like atom on the basis of (19a), (22a), (25a) and (26a) are:
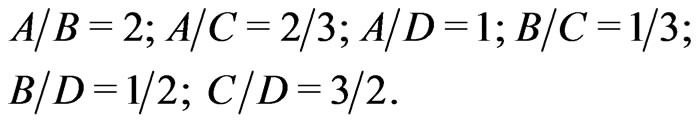 (64)
(64)
These ratios can be compared with similar ratios obtained for planets and satellites. We find (see Tables 5 and 6) that 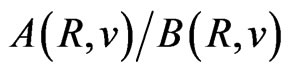 is very close to 2 and the ratio
is very close to 2 and the ratio  is very close to 3/2. The remaining ratios of (64), viz.
is very close to 3/2. The remaining ratios of (64), viz.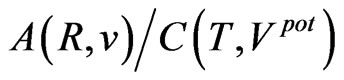 ,
,  ,
, 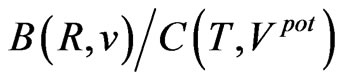 and
and 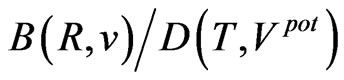 are presented in Tables 7 and 8. They are plainly close to the corresponding ratios (64). This agreement is evident especially in the case of planets; see Table 7.
are presented in Tables 7 and 8. They are plainly close to the corresponding ratios (64). This agreement is evident especially in the case of planets; see Table 7.
In the case of satellites the strongest deviations of the observed data from the ratios (64) are obtained for the pairs of Deimos-Phobos and Iapetus-Titan (see Table 8).
Another ratio, similar to that calculated in (53) for the areas (48)-(51), can be calculated for the areas (58)-(61). This is
 (65)
(65)
Its values for different planetary and satellitary pairs

Table 4. Ratios between the averaged belt areas calculated for planets and satellites. Column first: the ratios of energy-time and momentum-position phase spaces calculated according to the Formula (53). Column second: the ratios of potential-time and velocity-position phase spaces calculated according to (65). The ratios  and
and 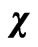 approach a similar ratio calculated for the atomic electron orbits in (66).
approach a similar ratio calculated for the atomic electron orbits in (66).
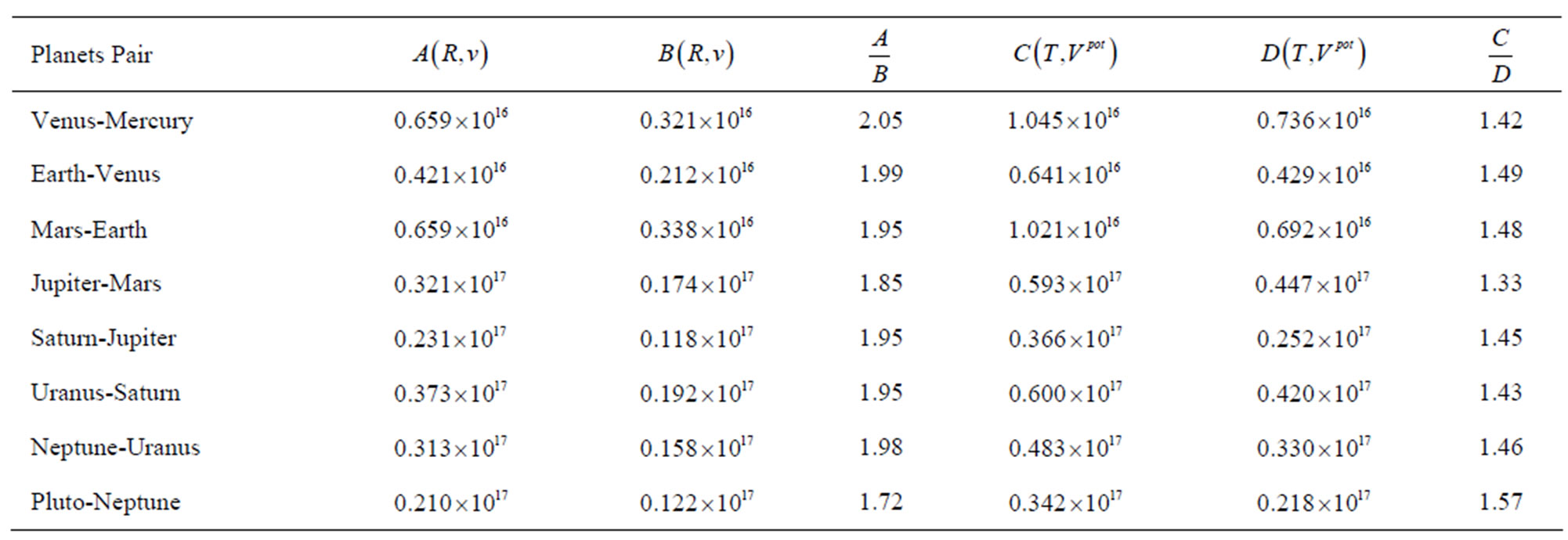
Table 5. Belt areas between the neighbouring planet orbits calculated (in Jkg–1s) for the velocity-position and potential-time phase spaces; for A(R,v) and B(R,v) see Equations (58) and (59); for C(T,Vpot) and D(T,Vpot) see, respectively, (60) and (61). The input data are equal to those applied in calculating Table 1. The ratios A/B and C/D have their counterparts in the data of the Bohr-Sommerfeld theory given in (64). These are A/B = 2 and C/D = 3/2.
are listed in Table 4. On the basis of calculations done in the Bohr-Sommerfeld theory of the hydrogen-like atom the values of 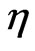 given by (53) and those of
given by (53) and those of 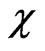 given by (65) should approach the same value
given by (65) should approach the same value
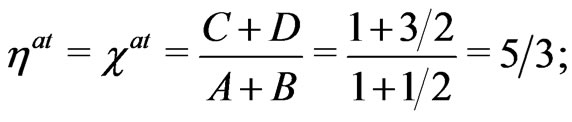 (66)
(66)
see (19a), (22a), (25a) and (26a) at the end of Section 4.
6. Discussion
The aim of the present paper was to detect, and check, some regularities which can be obtained for the fragments of the phase-space areas defined by parameters characteristic for the motion of celestial bodies in the solar system. In this search we were guided by similar phase-space properties derived for the electron motion in

Table 6. Belt areas between the neighbouring satellite orbits calculated (in Jkg–1s) for the velocity-position and potential-time phase spaces; for A(R,v) and B(R,v) see Equations (58) and (59); for C(T,Vpot) and D(T,Vpot) see, respectively, (60) and (61). The input data are equal to those applied in calculating Table 2. The ratios A/B and C/D have their counterparts in the data of the Bohr-Sommerfeld theory given in (64). These are A/B = 2 and C/D = 3/2.
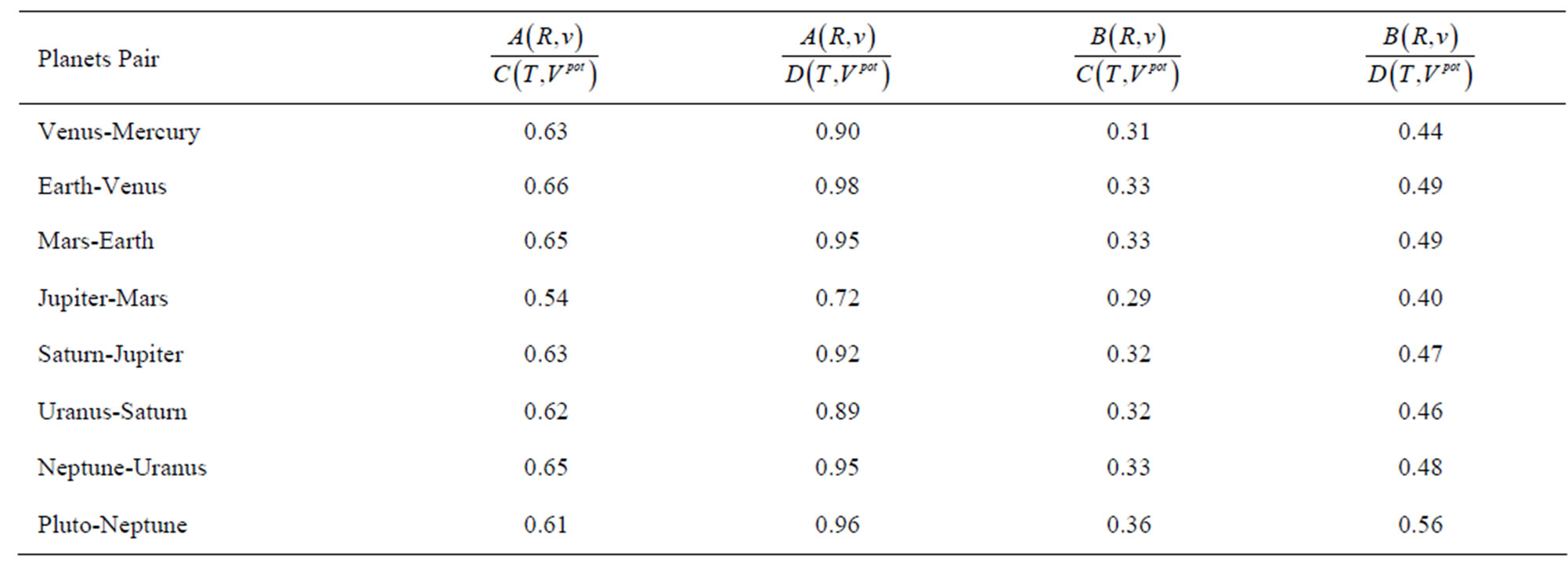
Table 7. The ratios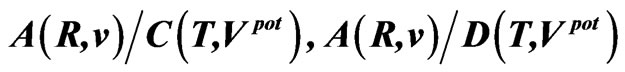 ,
,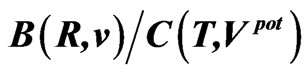 and
and 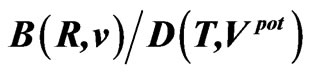 calculated for the belt areas of the velocity-position and potential-time spaces for planets. These ratios, as well as those calculated in Table 5, approach the ratios of the phase-space areas obtained from the electron orbits in the Bohr-Sommerfeld atom; see (64).
calculated for the belt areas of the velocity-position and potential-time spaces for planets. These ratios, as well as those calculated in Table 5, approach the ratios of the phase-space areas obtained from the electron orbits in the Bohr-Sommerfeld atom; see (64).
the Bohr-Sommerfeld atom. The calculations applied the data calculated from [5] and those listed in Tables 1 and 2 in [6]. However, several printing errors were discovered in Table 2 of the last reference for the data of Iapetus, the satellite of Saturn, and Titania and Oberon, the satellites of Uranus. The corrected data are given in Table 3 of the present paper.
For planets the belt areas defined in the momentumposition and energy-time phase spaces exhibit their ratios 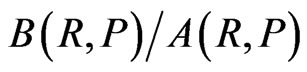 and
and 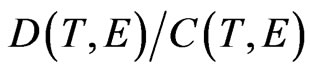 [see (48)-(51)] considerably different from unity only for Earth-Venus, Mars-Earth, Neptune-Uranus, and Pluto-Neptune pairs; see Table 1. Similar belts for the phase-space areas defined for the neighbouring orbits of the satellites (Table 2) show the ratios
[see (48)-(51)] considerably different from unity only for Earth-Venus, Mars-Earth, Neptune-Uranus, and Pluto-Neptune pairs; see Table 1. Similar belts for the phase-space areas defined for the neighbouring orbits of the satellites (Table 2) show the ratios 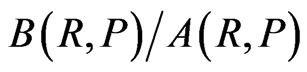 and
and  still closer to unity than in the planet
still closer to unity than in the planet

Table 8. The ratios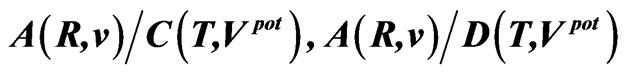 ,
, 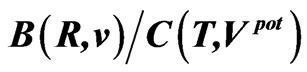 and
and 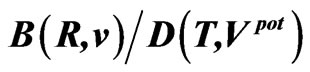 calculated for the belt areas of the velocity-position and potential-time spaces for satellites. These ratios, as well as those calculated in Table 6, approach the ratios of the phase-space areas obtained from the electron orbits in the Bohr-Sommerfeld atom; see (64).
calculated for the belt areas of the velocity-position and potential-time spaces for satellites. These ratios, as well as those calculated in Table 6, approach the ratios of the phase-space areas obtained from the electron orbits in the Bohr-Sommerfeld atom; see (64).
case. The only strong deviations from unity are exhibited for the satellite pairs of Thetys-Enceladus, Dione-Thetys and Ariel-Miranda.
Some properties concerning the belt areas in the phasespace and their ratios can be deduced in an analytic way. For example, an approximate equivalence between 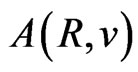 and
and  [see (58) and (60)] can be attained on condition
[see (58) and (60)] can be attained on condition 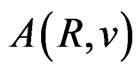 is multiplied by the factor of 3/2. For, from (58) and (62) we obtain:
is multiplied by the factor of 3/2. For, from (58) and (62) we obtain:
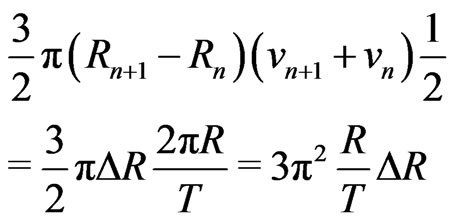 (67)
(67)
where
 (68)
(68)
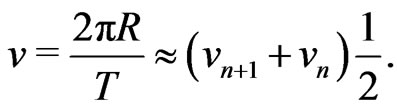 (69)
(69)
Similarly, from (60) and (63):
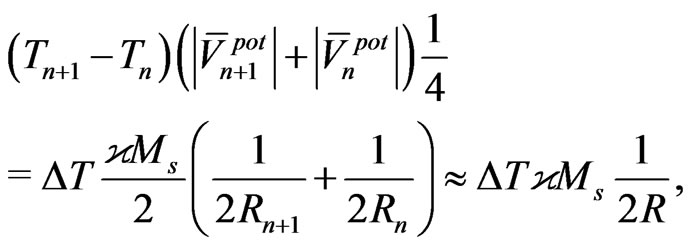 (70)
(70)
where  is the gravitational constant. Here
is the gravitational constant. Here
 (71)
(71)
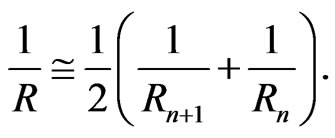 (72)
(72)
From the Kepler’s law (see e.g. [4])
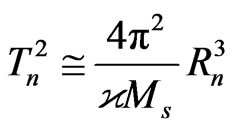 (73)
(73)
We obtain by differentiation the relation:
 (74)
(74)
valid approximately for any n. A substitution of (74) into (70) gives
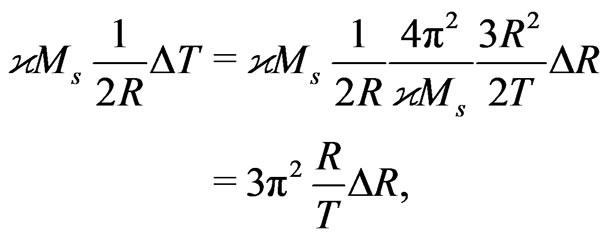 (75)
(75)
which is identical to (67). Hence, the ratio between 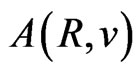 and
and 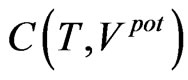 [see (58) and (60)] should be approximately equal to
[see (58) and (60)] should be approximately equal to
 (76)
(76)
which is the result obtained also for 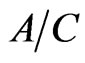 in the atom on the basis of (19a) and (25a). In calculations we took into account the fact that the average
in the atom on the basis of (19a) and (25a). In calculations we took into account the fact that the average 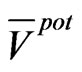 entering (63) are not much different from the actual
entering (63) are not much different from the actual 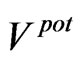 because of a quasi-circular character of the orbit possessed by a moving body.
because of a quasi-circular character of the orbit possessed by a moving body.
Other ratios than 2/3 given in (76) can be deduced between the areas (58), (59) and (60), (61). These ratios are identical to the ratios between the belt areas (34), (37), (40) and (41) [or (19a), (22a), (25a) and (26a)] obtained for the Bohr-Sommerfeld hydrogen atom; see (64). In Tables 7 and 8 we calculate these ratios for the planetary and satellitary systems.
A characteristic point is that the ratios calculated in Tables 7 and 8 are only feebly dependent on the choice of the planetary or satellitary pair. In this sense these ratios have an almost constant character similar to that postulated at the end of Section 1.
In particular, the average deviations of the ratios in Tables 7 and 8 from the ratios calculated in (64) are respectively:
 (77)
(77)
 (78)
(78)
 (79)
(79)
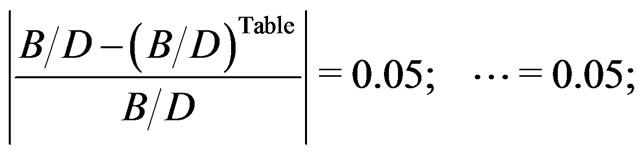 (80)
(80)
The first numbers calculated in (77)-(80) concern the data taken from Table 7, the second numbers concern the data taken from Table 8.
REFERENCES
- J. C. Slater, “Quantum Theory of Atomic Structure,” McGraw-Hill, New York, 1960.
- L. D. Landau and E. M. Lifshitz, “Mechanics,” Pergamon Press, Oxford, 1960.
- A. Sommerfeld, “Mechanik (in German),” Akademische Verlagsgesellschaft, Leipzig, 1943.
- V. M. Blanco and S. W. McCuskey, “Basic Physics of the Solar System,” Addison-Wesley, Reading, 1961.
- K. L. Lang, “Astrophysical Data: Planets and Stars,” Springer, New York, 1991.
- S. Olszewski, “Equivalence of Energy-Time and Momentum-Position Phase Spaces of the Solar System,” Earth, Moon and Planets, Vol. 74, No. 2, 1996, pp. 151-173. doi:10.1007/BF00056411
- A. Sommerfeld, “Atombau und Spektrallinien,” Vol. 1, 5th Edition, Vieweg, Braunschweig, 1931.

