Journal of Modern Physics
Vol.3 No.7(2012), Article ID:21118,7 pages DOI:10.4236/jmp.2012.37075
Theory of Zero-Resistance States Generated by Radiation in GaAs/AlGaAs
1Department of Physics, University at Buffalo, Buffalo, USA
2Research Division, National Center for University Entrance Examinations, Tokyo, Japan
3Department of Physics, Faculty of Science, Tokyo University of Science, Tokyo, Japan
Email: *asuzuki@rs.kagu.tus.ac.jp
Received May 5, 2012; revised June 10, 2012; accepted July 1, 2012
Keywords: superconducting (zero-resistance) states; composite-boson (fermion); B-linear Hall resistivity; phonon exchange
ABSTRACT
Mani observed zero-registance states similar to those quantum-Hall-effect states in GaAs/AlGaAs but without the Hall resistance plateaus upon the application of radiations [R. G. Mani, Physica E 22, 1 (2004)]. An interpretation is presented. The applied radiation excites “holes”. The condensed composite (c)-bosons formed in the excited channel create a superconducting state with an energy gap. The supercondensate suppresses the non-condensed c-bosons at the higher energy, but it cannot suppress the c-fermions in the base channel, and the small normal current accompanied by the Hall field yeilds a B-linear Hall resistivity.
1. Introduction
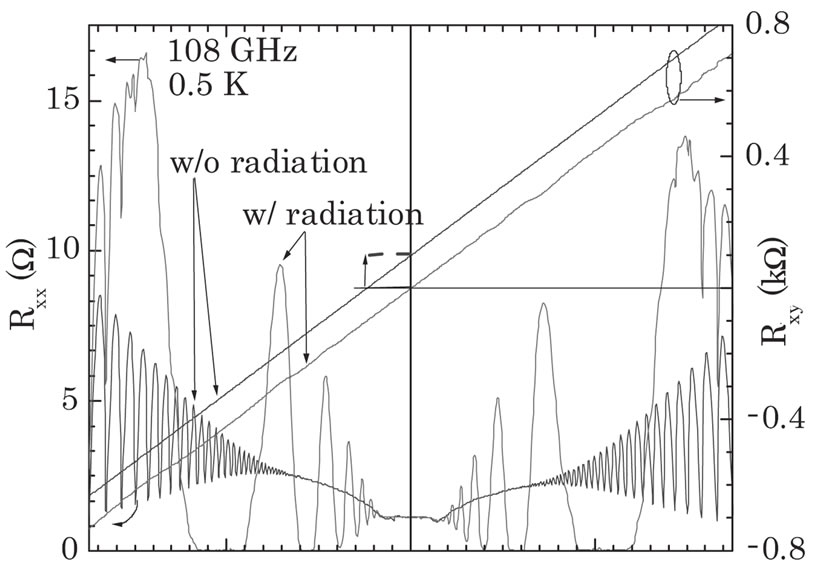
In 2002 Mani et al. [1] observed a set of zero-resistance (superconducting) states in GaAs/AlGaAs heterojunction subjected to radiations at the low temperatures (~1.5 K) and the relatively low magnetic fields (~0.2 T). Figure 1 represents the data obtained by Mani [2,3] for the Hall (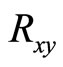 ) and diagonal (
) and diagonal (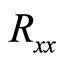 ) resistances in GaAs/AlGaAs at 50 GHz and 0.5 K. The resistance
) resistances in GaAs/AlGaAs at 50 GHz and 0.5 K. The resistance  rises exponentially and symmetrically on both sides of the fields centered at
rises exponentially and symmetrically on both sides of the fields centered at
 (1)
(1)
with ω = radiation frequency, m = effective mass, e = electron charge, indicating the superconducting state with an energy gap 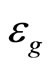 in the elementary excitation spectrum. The phenomenon is similar to that observed in the same system in the traditional quantum Hall effect (QHE) regime (T ~ 1.5 K, b ~ 10 T) [4] with the main difference that the superconducting states are not accompanied by the Hall resistivity plateaus for the system subjected to radiation, see Figures 1(a) and (b). We call the temperature below which the superconducting state appears the critical temperature
in the elementary excitation spectrum. The phenomenon is similar to that observed in the same system in the traditional quantum Hall effect (QHE) regime (T ~ 1.5 K, b ~ 10 T) [4] with the main difference that the superconducting states are not accompanied by the Hall resistivity plateaus for the system subjected to radiation, see Figures 1(a) and (b). We call the temperature below which the superconducting state appears the critical temperature . The critical temperature
. The critical temperature  (1.3 K) observed at
(1.3 K) observed at 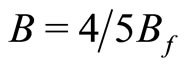 is considerably higher than the traditional QHE critical temperature (0.5 K). Zudov et al. [5] reported similar magnetotransport properties for the system subjected to radiations with slightly different experimental conditions. They suggested that the principal resistivity minima occur at
is considerably higher than the traditional QHE critical temperature (0.5 K). Zudov et al. [5] reported similar magnetotransport properties for the system subjected to radiations with slightly different experimental conditions. They suggested that the principal resistivity minima occur at
 (2)
(2)
rather than 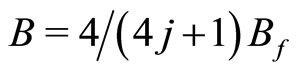 (Mani’s case). They also noted a noticeable side resistivity minimum besides the principal set of the minima.
(Mani’s case). They also noted a noticeable side resistivity minimum besides the principal set of the minima.
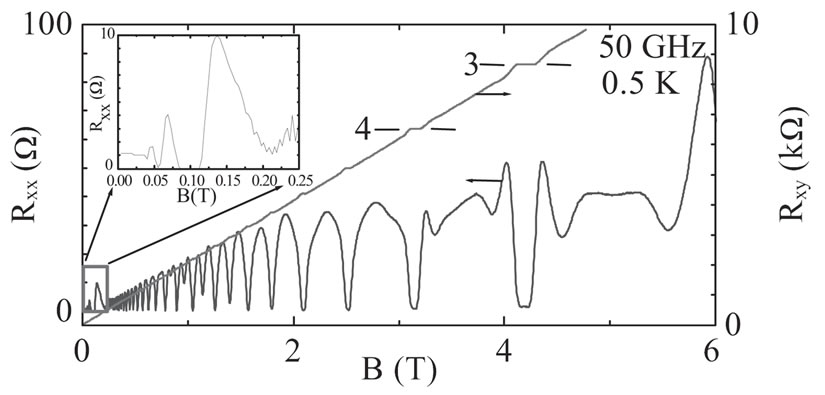
In finer analysis Mani et al. [6] observed, see Figure 2, that (a) the deviation in the Hall resistance
 (3)
(3)
correlates with the resistance 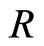 such that
such that 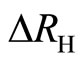 nearly vanishes when
nearly vanishes when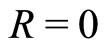 , and (b)
, and (b)  is negative, and it is antisymmetric with respect to small B-fields:
is negative, and it is antisymmetric with respect to small B-fields:
 (4)
(4)
The property (b) means that there is a current due to “hole”-like particles having the charge of the opposite sign to that of the majority (“electron”-like) current carrier. In other words the applied radiation generates the “holes”. This may be checked by applying the circularly polarized lasers, which can excite “electrons” or “holes” selectively, depending on the sense of the circular polarization. The small slope 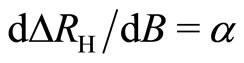 means that the “hole” density is considerable higher than the “electron”
means that the “hole” density is considerable higher than the “electron”
 (a)
(a)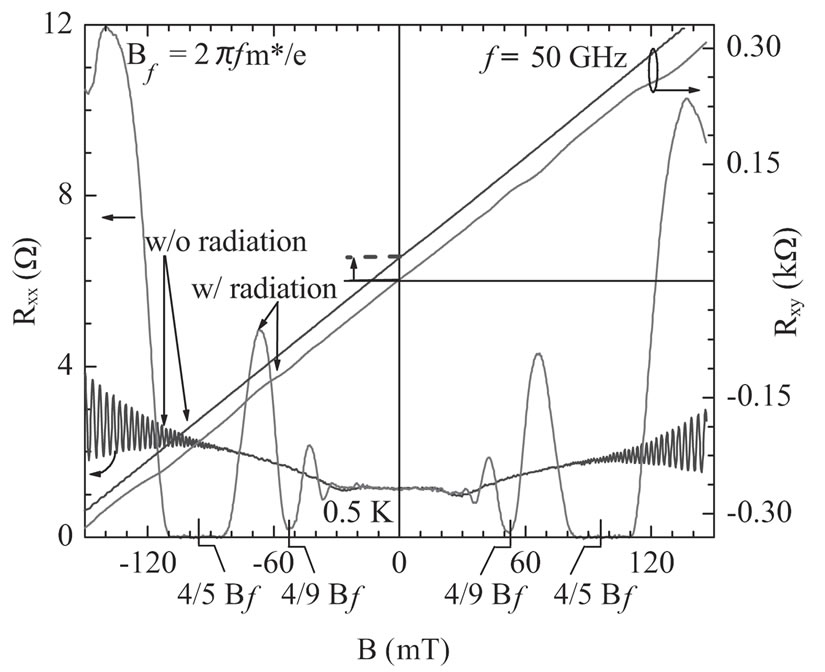 (b)
(b)
Figure 1. (a) The Hall (Rxy) and diagonal (Rxx) resistances in a GaAs/AlGaAs under radiation at 50 GHz after Mani [2]. Quantum Hall effects (QHE) occur at high b as Rxx vanishes. Inset; An expanded view of the low b data; (b) Data over low magnetic fields obtained both with (w/) and without (w/o) radiation at 50 GHz. Here, radiation induced vanishing resistance around (4/5)Bf does not induce plateaus in the Hall resistance, unlike in QHE. Yet, there are clear microwave induced oscillations in the Hall effect.
density.
Mani et al. [1] suggested for the cause of the spectral gap the electron pairing due to the excitons induced by radiation. Other mechanisms were proposed by several theoretical groups [7-11]. But none of them are conclusive. In particular no explanation is given to the question why the superconducting state can occur without the Hall resistivity plateau.
Earlier Fujita et al. [12] developed a microscopic theory of the QHE based on the electron (fluxon)-phonon interaction. In this theory the composite (c-)particles (bosons or fermions) having a conduction electron and a number of flux quanta (fluxons) are bound by the phonon-exchange attraction. The composite moves as a boson (fermion) according to whether it contains the odd (even) number of fluxons in it. At the Landau Level (LL) occupation number (filling factor) ,
, 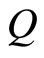 odd, the c-bosons, each with
odd, the c-bosons, each with 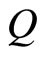 fluxons, are generated, and condense below the critical temperature
fluxons, are generated, and condense below the critical temperature . The Hall resistivity plateau is due to the Meissner effect, as explained below.
. The Hall resistivity plateau is due to the Meissner effect, as explained below.
 (a)
(a)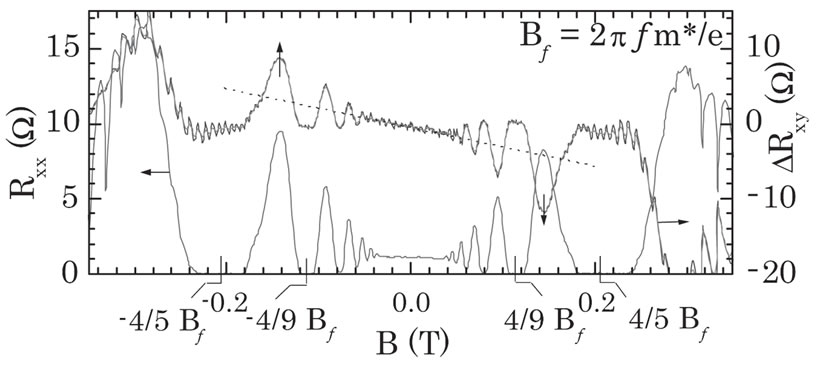 (b)
(b)
Figure 2. (a) Transport measurements with (w/) and without (w/o) microwave radiation at f = 108 GHz after Mani et al. [6]. Radiation induced vanishing Rxx is observable around (4/5)Bf and (4/9)Bf. A comparison of the w/ and w/o radiation Rxy indicates antisymmetric-in-b oscillations in Rxy under photoexcitation, which correlate with the Rxx oscillations. Here, the w/o radiation Hall data have been offset for the sake of clarity; (b) The radiation induced change in the Hall resistance, ΔRxy, is shown along with Rxx. Note the antisymmetric-in-b ΔRxy oscillations.
In the present work we shall extend our theory to Mani’s phenomena. We show that the most prominent zero-resistance states observed by Mani et al. [1] and Du et al. [3] represents the integer QHE with the 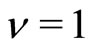 state corresponding to the superconducting state at
state corresponding to the superconducting state at 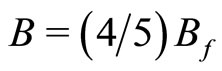 in Mani’s case (the state
in Mani’s case (the state 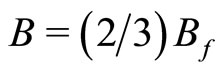 in Du’s case). If we write
in Du’s case). If we write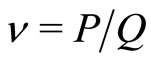 , the Mani-series 4/(4j + 1) can be recovered by setting
, the Mani-series 4/(4j + 1) can be recovered by setting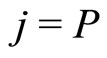 ,
, . Our model explains why the superconducting state under radiation does not accompany the Hall resistivity plateau. We predict that the fractional QHE should exist for
. Our model explains why the superconducting state under radiation does not accompany the Hall resistivity plateau. We predict that the fractional QHE should exist for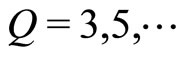 . The aformentioned side dip observed by Zudov et al. [5] should correspond to the state at
. The aformentioned side dip observed by Zudov et al. [5] should correspond to the state at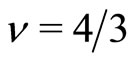 . This dip is missing in Mani et al.’s experiments. This is because the experimental temperature
. This dip is missing in Mani et al.’s experiments. This is because the experimental temperature  K is so low that the dip is overshadowed by the bosonic state at
K is so low that the dip is overshadowed by the bosonic state at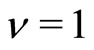 .
.
2. Theory of the Quantum Hall Effect
If the magnetic field is applied slowly, the classical electron can continuously change from the straight line motion at zero field to the curved motion at a finite B. Quantum mechanically, the change from the momentum state to the Landau state requires a perturbation. We choose for this perturebation the phonon exchange between the electron and the fluxon. Consider the cparticle with a few fluxons. If the B-field is applied slowly the energy of the electron does not change but the cyclotron motion always acts so as to reduce the magnetic fields. Hence the total energy of the c-particle is less than the electron energy plus the unperturbed field energy. In other words the c-particle is stable against the break-up, and it is in a bound (negative energy) state. In our theory a c-particle is simply a dressed electron carrying  fluxons. The c-particle moves as a boson (fermion) depending on the odd (even) number of fluxons in it. At the Landau level (LL) occupation number
fluxons. The c-particle moves as a boson (fermion) depending on the odd (even) number of fluxons in it. At the Landau level (LL) occupation number ,
,  odd, the c-bosons with
odd, the c-bosons with  fluxons are generated, and condense below certain critical temperature
fluxons are generated, and condense below certain critical temperature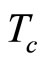 . The Hall resistivity plateau is due to the Meissner effect, see below.
. The Hall resistivity plateau is due to the Meissner effect, see below.
GaAs forms a zinc blende lattice. We assume that the interface is in the plane (001). The  ions form a square lattice with the sides directed in [110] and [1
ions form a square lattice with the sides directed in [110] and [1 0]. The “electron” (wave packet) will then move isotropically with an effective mass
0]. The “electron” (wave packet) will then move isotropically with an effective mass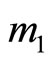 . The
. The 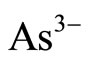 ions also form a square lattice at a different height in [001]. The “holes”, each having a positive charge, will move similarly with an effective mass
ions also form a square lattice at a different height in [001]. The “holes”, each having a positive charge, will move similarly with an effective mass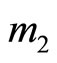 . A longitudinal phonon moving in [110] or in [1
. A longitudinal phonon moving in [110] or in [1 0] can generate a charge (current) density variations, establishing an interaction between the phonon and the electron (phonon). If one phonon exchange is considered between the electron and the fluxon, a second-order perturbation calculation establishes an effective electron-fluxon interaction [14]:
0] can generate a charge (current) density variations, establishing an interaction between the phonon and the electron (phonon). If one phonon exchange is considered between the electron and the fluxon, a second-order perturbation calculation establishes an effective electron-fluxon interaction [14]:
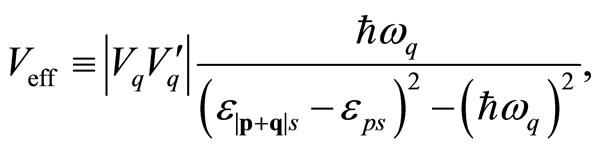 (5)
(5)
where 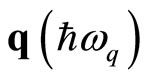 is the phonon momentum (energy);
is the phonon momentum (energy); 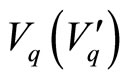 the interaction strength between the electron (fluxon) and the phonon; the Landau quantum number
the interaction strength between the electron (fluxon) and the phonon; the Landau quantum number  is omitted; the bold
is omitted; the bold 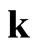 denotes the two dimensional (2D) guiding center momentum and the italic
denotes the two dimensional (2D) guiding center momentum and the italic 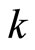 the magnitude. If the energies (
the magnitude. If the energies ( ) of the final and initial electron states are equal as in the degenerate LL, the effective interaction is attractive, i.e.,
) of the final and initial electron states are equal as in the degenerate LL, the effective interaction is attractive, i.e., 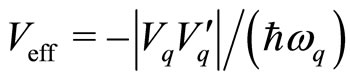 .
.
Following Bardeen, Cooper and Schrieffer (BCS) [13], we start with a Hamiltonian h with the phonon variables eliminated:
 (6)
(6)
where 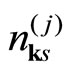 is the number operator for the “electron” (1) [“hole” (2), fluxon (3)] at momentum
is the number operator for the “electron” (1) [“hole” (2), fluxon (3)] at momentum 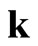 and spin
and spin  with the energy
with the energy . We represent the “electron” (“hole”) number
. We represent the “electron” (“hole”) number 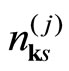 by
by  †
†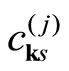 , where
, where  are annihilation (creation) operators satisfying the Fermi anticommutation rules:
are annihilation (creation) operators satisfying the Fermi anticommutation rules:
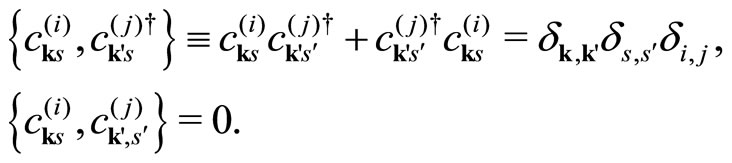 (7)
(7)
We represent the fluxon number  by
by , with
, with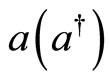 , satisfying the anticommutation rules.
, satisfying the anticommutation rules.  ,
, . The prime on the summation means the restriction:
. The prime on the summation means the restriction: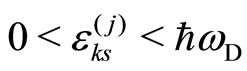 ,
, 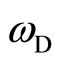 = Debye frequency. If the fluxons are replaced by the conduction electrons (“electrons”, “holes”) our Hamiltonian
= Debye frequency. If the fluxons are replaced by the conduction electrons (“electrons”, “holes”) our Hamiltonian  is reduced to the original BCS Hamiltonian, Equation (2.14) of Ref. [13]. The “electron” and “hole” are generated, depending on the energy contour curvature sign [14]. For example only “electrons” (“holes”), are generated for a circular Fermi surface with the negative (positive) curvature whose inside (outside) is filled with electrons. Since the phonon has no charge, the phonon exchange cannot change the net charge. The pairing interaction terms in Equation (2) conserve the charge. The term
is reduced to the original BCS Hamiltonian, Equation (2.14) of Ref. [13]. The “electron” and “hole” are generated, depending on the energy contour curvature sign [14]. For example only “electrons” (“holes”), are generated for a circular Fermi surface with the negative (positive) curvature whose inside (outside) is filled with electrons. Since the phonon has no charge, the phonon exchange cannot change the net charge. The pairing interaction terms in Equation (2) conserve the charge. The term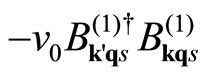 , where
, where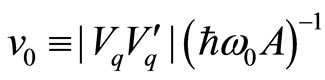 , A = sample area, is the pairing strength, generates the transition in the “electron” states. Similary, the exchange of a phonon generates a transition in the “hole” states, represented by
, A = sample area, is the pairing strength, generates the transition in the “electron” states. Similary, the exchange of a phonon generates a transition in the “hole” states, represented by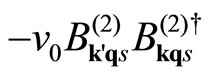 . The phonon exchange can also pair-create and pair-annihilate “electron” (“hole”)- fluxon composites, represented by
. The phonon exchange can also pair-create and pair-annihilate “electron” (“hole”)- fluxon composites, represented by ,
,  . At 0 K the system can have equal numbers of
. At 0 K the system can have equal numbers of  c-bosons, “electrons” (“holes”) composites, generated by
c-bosons, “electrons” (“holes”) composites, generated by .
.
The c-bosons, each with one fluxon, will be called the fundamental (f) c-bosons. Their energies  are obtained from [14]
are obtained from [14]
 (8)
(8)
where 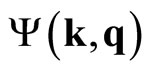 is the reduced wavefunction for the fcboson; we neglected the fluxon energy. The
is the reduced wavefunction for the fcboson; we neglected the fluxon energy. The  denotes the strength after the ladder diagram binding, see below. For small
denotes the strength after the ladder diagram binding, see below. For small , we obtain
, we obtain
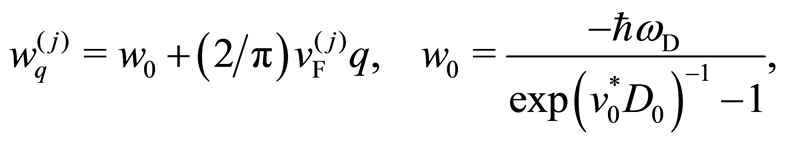 (9)
(9)
where 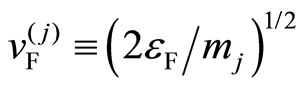 is the Fermi velocity and
is the Fermi velocity and  the density of states per spin. Note that the energy
the density of states per spin. Note that the energy 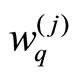 depends linearly on the momentum
depends linearly on the momentum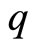 .
.
The system of free fc-bosons undergoes a Bose-Einstein condensation (BEC) in 2D at the critical temperature [13]
 (10)
(10)
The interboson distance  calculated from this expression is
calculated from this expression is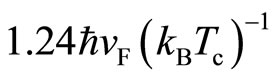 . The boson size
. The boson size 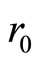 calculated from Equation (4), using the uncertainty relation
calculated from Equation (4), using the uncertainty relation  and
and , is
, is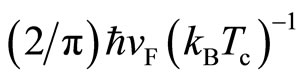 , which is a few times smaller than
, which is a few times smaller than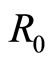 . Hence, the bosons do not overlap in space, and the model of free bosons is justified. For GaAs/AlGaAs,
. Hence, the bosons do not overlap in space, and the model of free bosons is justified. For GaAs/AlGaAs, 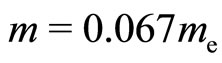 , me = electron mass. For the 2D electron density 1011 cm−2, we have
, me = electron mass. For the 2D electron density 1011 cm−2, we have 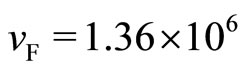 cm∙s−1. Not all electrons are bound with fluxons since the simultaneous generations of ±fc-bosons is required. The minority carrier (“hole”) density controls the fc-boson density. For
cm∙s−1. Not all electrons are bound with fluxons since the simultaneous generations of ±fc-bosons is required. The minority carrier (“hole”) density controls the fc-boson density. For  cm−2,
cm−2, 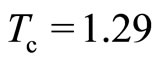 K, which is reasonable.
K, which is reasonable.
In the presence of Bose condensate below 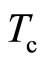 the unfluxed electron carries the energy
the unfluxed electron carries the energy , where the quasi-electron energy gap
, where the quasi-electron energy gap  is the solution of
is the solution of
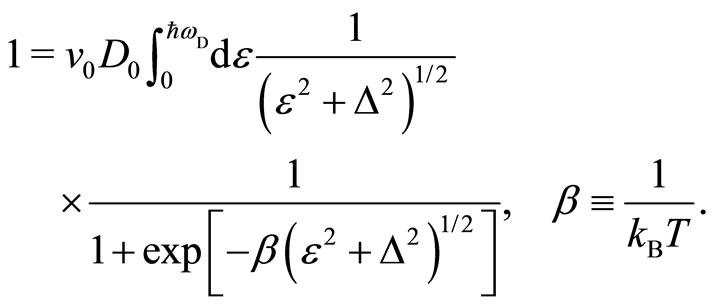 (11)
(11)
Note that the gap  depends on
depends on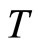 . At
. At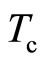 , there is no condensate and hence
, there is no condensate and hence  vanishes.
vanishes.
Now the moving fc-boson below 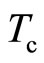 has the energy
has the energy 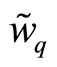 obtained from
obtained from
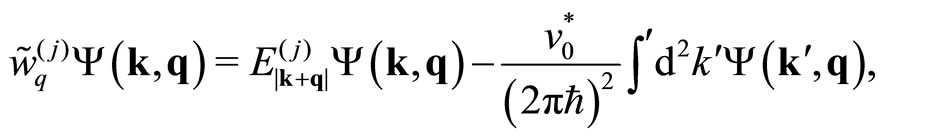 (12)
(12)
where 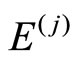 replaced
replaced 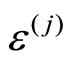 in Equation (3). We obtain
in Equation (3). We obtain
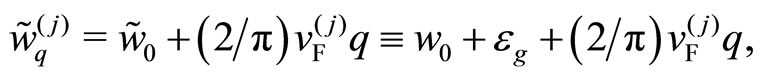 (13)
(13)
where 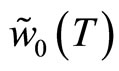 is determined from
is determined from
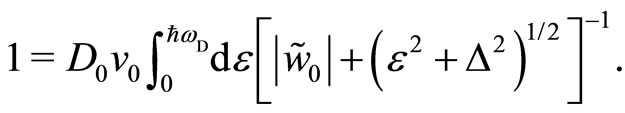 (14)
(14)
The energy difference:
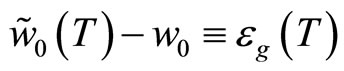 (15)
(15)
represents the T-dependent energy gap. The energy 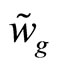 is negative. Otherwise, the fc-boson should break up. This limits
is negative. Otherwise, the fc-boson should break up. This limits 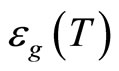 to be
to be 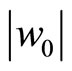 at 0 K. The
at 0 K. The 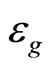 declines to zero as the temperature approaches
declines to zero as the temperature approaches  from below.
from below.
The fc-boson, having the linear dispersion (12), can move in all directions in the plane with the constant speed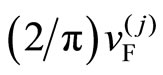 . The supercurrent is generated by the
. The supercurrent is generated by the  fc-bosons condensed monochromatically at the momentum directed along the sample length. The supercurrent density (magnitude)
fc-bosons condensed monochromatically at the momentum directed along the sample length. The supercurrent density (magnitude)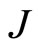 , calculated by the rule:
, calculated by the rule: , is
, is
 (16)
(16)
The induced Hall field (magnitude) 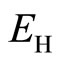 equals
equals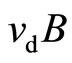 . The magnetic flux is quantized
. The magnetic flux is quantized ,
, 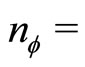 fluxon density. Hence we obtain
fluxon density. Hence we obtain
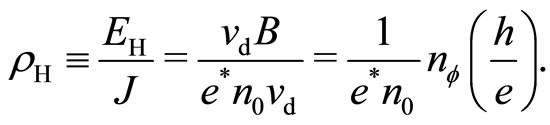 (17)
(17)
If ,
, 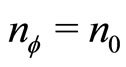 , we obtain
, we obtain  in agreement with the plateau value observed.
in agreement with the plateau value observed.
The model can be extended to the integer QHE at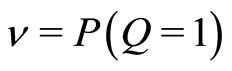 . The field magnitude is less. The LL degeneracy
. The field magnitude is less. The LL degeneracy  is linear in
is linear in , and hence the lowest
, and hence the lowest  LL’s must be considered. The fc-boson density
LL’s must be considered. The fc-boson density  per LL is the electron density
per LL is the electron density 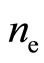 over
over  and the fluxon density
and the fluxon density 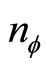 is the boson density
is the boson density 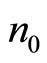 over
over :
:
 (18)
(18)
At  there are c-bosons, each with two fluxons. The c-fermions have a Fermi energy. The
there are c-bosons, each with two fluxons. The c-fermions have a Fermi energy. The  c-fermions have effective masses. The Hall resistivity
c-fermions have effective masses. The Hall resistivity 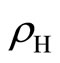 has a b-linear behavior while the resistivity
has a b-linear behavior while the resistivity 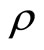 is finite.
is finite.
Let us now take a general case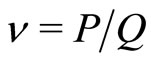 , odd
, odd . Assume that there are
. Assume that there are  sets of c-fermions with
sets of c-fermions with 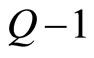 fluxons, which occupy the lowest
fluxons, which occupy the lowest  LL’s. The cfermions subject to the available B-field form c-bosons with
LL’s. The cfermions subject to the available B-field form c-bosons with 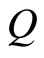 fluxons. In this configuration the c-boson density
fluxons. In this configuration the c-boson density 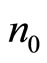 and the fluxon density
and the fluxon density 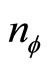 are given by Equations (18). Using Equations (17) and (18) and assuming the fractional charge [15,16]
are given by Equations (18). Using Equations (17) and (18) and assuming the fractional charge [15,16]
 (19)
(19)
we obtain
 (20)
(20)
as observed. In our theory the integer  denotes the number of fluxons in the c-boson and the integer
denotes the number of fluxons in the c-boson and the integer  the number of the LL’s occupied by the parental c-fermions, each with
the number of the LL’s occupied by the parental c-fermions, each with 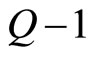 fluxons.
fluxons.
Our Hamiltonian in Equation (6) can generate and stabilize the c-particles with an arbitrary number of fluxons. For example a c-fermion with two fluxons is generated by two sets of the ladder diagram bindings, each between the electron and the fluxon. The ladder diagram binding arises as follows. Consider a hydrogen atom. The Hamiltonian contains kinetic energies of the electron and the proton, and the attractive Coulomb interaction. If we regard the Coulomb interaction as a perturbation and use a perturbation theory, we can represent the interaction process by an infinite set of ladder diagrams, each ladder step connecting the electron and the proton. The energy eigenvalues of this system is not obtained by using the perturbation theory but they are obtained by solving the Schrödinger equation directly. This example indicates that a two-body bound state is represented by an infinite set of ladder diagrams and that the binding energy (the negative of the ground-state energy) is calculated by a non-perturbative method.
Jain introduced the effective magnetic field [17-19]
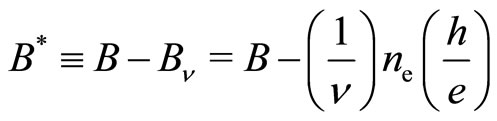 (21)
(21)
relative to the standard field for the composite (c-) fermion at the even-denominator fraction. We extend this to the bosonic (odd-denominator) fraction. This means that the c-particle moves field-free at the exact fraction. The c-particle is viewd as the quasiparticle containing an electron circulating around 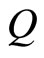 fluxons. The jumping of the guiding centers (the CM of the c-particle) can occur as if they are subject to no B-field at the exact fraction. The excess (or deficit) of the magnetic field is simply the effective magnetic field B. The plateau in
fluxons. The jumping of the guiding centers (the CM of the c-particle) can occur as if they are subject to no B-field at the exact fraction. The excess (or deficit) of the magnetic field is simply the effective magnetic field B. The plateau in 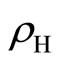 is formed due to the Meissner effect. Consider the case of zero temperature near
is formed due to the Meissner effect. Consider the case of zero temperature near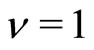 . Only the energy
. Only the energy  matters. The fc-bosons are condensed with the ground-state energy
matters. The fc-bosons are condensed with the ground-state energy , and hence the system energy
, and hence the system energy 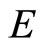 at
at  is
is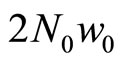 , where
, where 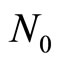 is the number of –fc-bosons (or
is the number of –fc-bosons (or 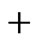 fc-bosons). The factor 2 arises since there are ±fcbosons. Away from
fc-bosons). The factor 2 arises since there are ±fcbosons. Away from 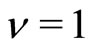 we must add the magnetic field energy
we must add the magnetic field energy , so that
, so that
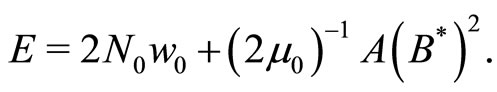 (22)
(22)
When the field is reduced, the system tries to keep the same number 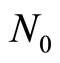 by sucking in the flux lines. Thus the magnetic field becomes inhomogeneous outside the sample, generating the magnetic field energy
by sucking in the flux lines. Thus the magnetic field becomes inhomogeneous outside the sample, generating the magnetic field energy  . If the field is raised, the system tries to keep the same number
. If the field is raised, the system tries to keep the same number 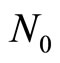 by expeling out the flux lines. The inhomogeneous fields outside raise the field energy as well. There is a critical field
by expeling out the flux lines. The inhomogeneous fields outside raise the field energy as well. There is a critical field . Beyond this value, the superconducting state is destroyed, generating a symmetric exponential rise in
. Beyond this value, the superconducting state is destroyed, generating a symmetric exponential rise in . In our discussion of the Hall resistivity plateau we used the fact that the ground-state energy
. In our discussion of the Hall resistivity plateau we used the fact that the ground-state energy  of the fc-boson is negative, that is, the c-boson is bound. Only then the critical field
of the fc-boson is negative, that is, the c-boson is bound. Only then the critical field  can be defined. Here the phonon exchange attraction played an important role. The repulsive Coulomb interaction, which is the departure point of the prevalent theories [12], cannot generate a bound state.
can be defined. Here the phonon exchange attraction played an important role. The repulsive Coulomb interaction, which is the departure point of the prevalent theories [12], cannot generate a bound state.
In the presence of the supercondensate the noncondensed c-boson has an energy gap . Hence the noncondensed c-boson density has the activation energy type exponential temperature-dependence:
. Hence the noncondensed c-boson density has the activation energy type exponential temperature-dependence:
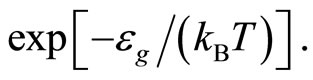 (23)
(23)
In the prevalent theories the energy gap for the fractional QHE is identified as the sum of the creation energies of a quasi-electron and a quasi-hole [20-23]. With this view it is difficult to explain why the activationenergy type temperature dependence shows up in the steady-state quantum transport. Some authors argue that the energy gap 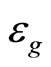 for the integer QHE is due to the LL separation =
for the integer QHE is due to the LL separation =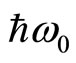 . But the separation
. But the separation 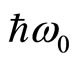 is much greater than the observed
is much greater than the observed . Besides from this view one cannot obtain the activation-type energy dependence.
. Besides from this view one cannot obtain the activation-type energy dependence.
The BEC occurs at each LL, and therefore the c-boson density  is less for high
is less for high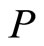 , see Equation (18), and the strengths become weaker as
, see Equation (18), and the strengths become weaker as 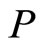 increases.
increases.
3. Quantum Hall Effect under Radiation
The experiments by Mani et al. [6] indicate that the applied radiation excites a large number of “holes” in the system. Using these “holes” and the preexisting “electrons” the phonon exchange can pair-create ±c-bosons, which condense below 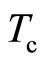 in the excited channel. The c-bosons condensed with the momentum along the sample length are responsible for the supercurrent. In the presence of the condensed c-bosons, the non-condensed c-bosons have an energy gap
in the excited channel. The c-bosons condensed with the momentum along the sample length are responsible for the supercurrent. In the presence of the condensed c-bosons, the non-condensed c-bosons have an energy gap , and therefore they are absent at 0 K. The c-fermions in the base channel have the energies
, and therefore they are absent at 0 K. The c-fermions in the base channel have the energies 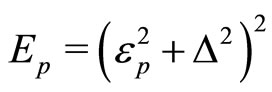 but their energy spectra have no gap. Hence they are not completely suppressed at the lowest temperatures. They contribute a small normal current. They are subject to the Lorentz force:
but their energy spectra have no gap. Hence they are not completely suppressed at the lowest temperatures. They contribute a small normal current. They are subject to the Lorentz force: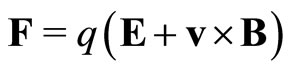 , and they generate a Hall field
, and they generate a Hall field 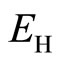 proportional to the field
proportional to the field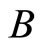 . Figure 2 show that the deviation in the Hall resistance,
. Figure 2 show that the deviation in the Hall resistance,  , is closely correlated to the resistance
, is closely correlated to the resistance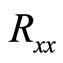 . We shall demonstrate this behavior based on the two channel (carriers) model.
. We shall demonstrate this behavior based on the two channel (carriers) model.
In the neighbarhood of the principal QHE at 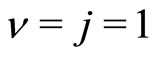 the carriers in the base and excited channels are respectively c-fermions and c-bosons condensed. The currents are additive. We write down the total current density
the carriers in the base and excited channels are respectively c-fermions and c-bosons condensed. The currents are additive. We write down the total current density  as the sum of the fermionic current density
as the sum of the fermionic current density 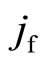 and the bosonic
and the bosonic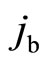 :
:
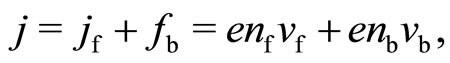 (24)
(24)
where 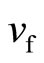 and
and 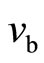 are the drift velocities of the fermions and bosons. The Hall fields
are the drift velocities of the fermions and bosons. The Hall fields  are additive, too. Hence we have
are additive, too. Hence we have
 (25)
(25)
We note that the Hall effect condition (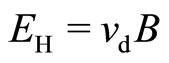 ) applies for the fermions and bosons. We therefore obtain
) applies for the fermions and bosons. We therefore obtain
 (26)
(26)
Far away from the midpoint of the zero-resistance stretch the c-bosons are absent and hence the Hall resistivity 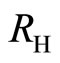 becomes
becomes 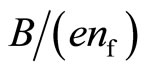 after the cancellation of
after the cancellation of . At the midpoint the c-bosons are dominant. Then, the Hall resistivity
. At the midpoint the c-bosons are dominant. Then, the Hall resistivity  is approximately
is approximately 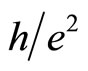 since
since
 (27)
(27)
where we used the flux quantization [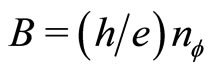 ], and the fact that the flux density
], and the fact that the flux density 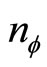 equals the c-boson density
equals the c-boson density . The Hall resistivity
. The Hall resistivity 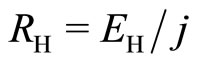 is not exactly equal to
is not exactly equal to 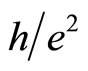 since the c-fermion current density
since the c-fermion current density  is much smaller than the supercurrent density
is much smaller than the supercurrent density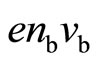 , but it does not vanish. In the horizontal stretch the system is superconducting, and hence the supercurrent dominates the normal current:
, but it does not vanish. In the horizontal stretch the system is superconducting, and hence the supercurrent dominates the normal current: . The deviation
. The deviation 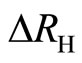 is, using Equation (26),
is, using Equation (26),
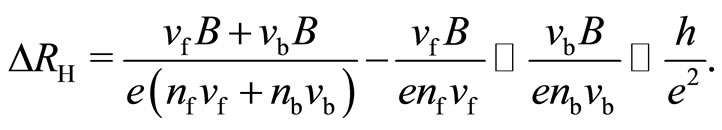 (28)
(28)
If the field  is raised (or lowered) a little from the midpoint,
is raised (or lowered) a little from the midpoint, 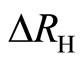 is a constant (
is a constant (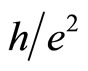 ) due to the Meissner effect. If the field is raised high enough, the superconducting state is destroyed and the normal current sets in, generating a finite resistance and a vanishing
) due to the Meissner effect. If the field is raised high enough, the superconducting state is destroyed and the normal current sets in, generating a finite resistance and a vanishing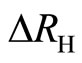 . Hence the deviation
. Hence the deviation 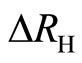 and the diagonal resistance
and the diagonal resistance  are closely correlated.
are closely correlated.
In Figure 2 we observe that in the range where the Shubnikov-de Haas (ShdH) oscilations are observed for the resistance without radiation, the signature of oscillations also appear for the resistance  with radiation. The ShdH oscillation arise only for the fermion carriers. The fermionic currents cannot be suppressed by the supercurrents. This ShdH signature in
with radiation. The ShdH oscillation arise only for the fermion carriers. The fermionic currents cannot be suppressed by the supercurrents. This ShdH signature in  should remain. Hence our two-channel model is supported.
should remain. Hence our two-channel model is supported.
Mani et al.’s experiments, Figure 2 of Ref. [1], show that the strength of the superconducting state does not change much for the radiation frequency 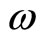 in the range (47, 110) GHz. This feature may come as follows. The 2D density of states for the conduction electrons associated with the circular Fermi surface is independent of the electron energy, and hence the number of the excited electrons is roughly independent of the radiation energy (frequency). The “hole”-like excitations are absent with no radiation. We suspect that the “hole”-band edge is a distance
in the range (47, 110) GHz. This feature may come as follows. The 2D density of states for the conduction electrons associated with the circular Fermi surface is independent of the electron energy, and hence the number of the excited electrons is roughly independent of the radiation energy (frequency). The “hole”-like excitations are absent with no radiation. We suspect that the “hole”-band edge is a distance  away from the system’s Fermi level. This means that if the radiation energy
away from the system’s Fermi level. This means that if the radiation energy 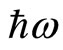 is less than
is less than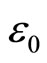 , the radiation can generate no superconducting state. This feature can be checked by applying radiation of frequencies lower than 47 GHz. Mani’s experiments on the simultaneous radiation excitations suggest that the critical frequency is between 15 and 47 GHz.
, the radiation can generate no superconducting state. This feature can be checked by applying radiation of frequencies lower than 47 GHz. Mani’s experiments on the simultaneous radiation excitations suggest that the critical frequency is between 15 and 47 GHz.
In summary the QHE under radiation is the QHE at the upper channel. The condensed c-bosons generate a superconducting state with a gap 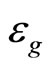 in the c-boson energy spectrum. The supercondensate changes the c-fermion energy from
in the c-boson energy spectrum. The supercondensate changes the c-fermion energy from 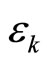 to
to  in the base channel. This energy spectrum has no gap, and hence the cfermions cannot be suppressed completely at the lowest temperatures, and generate a finite resistive current accompanied by the Hall field. This explains the b-linear Hall resistivity. Our microscopic theory can be tested experimentally by examining 1) the “hole”-like excitations by a circularly polarized laser; 2) the bosonic state at
in the base channel. This energy spectrum has no gap, and hence the cfermions cannot be suppressed completely at the lowest temperatures, and generate a finite resistive current accompanied by the Hall field. This explains the b-linear Hall resistivity. Our microscopic theory can be tested experimentally by examining 1) the “hole”-like excitations by a circularly polarized laser; 2) the bosonic state at  and
and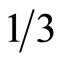 ; 3) the “hole” band edge.
; 3) the “hole” band edge.
REFERENCES
- R. G. Mani, J. H. Smet, K. von Klitzing, V. Narayanamurti, W. B. Johnson and V. Umansky, “Zero-Resistance States Induced by Electromagnetic-Wave Excitation in GaAs/AlGaAs Heterostructures,” Nature, Vol. 420, 2004, pp. 646-650. doi:10.1038/nature01277
- R. G. Mani, “Zero-Resistance States Induced by Electromagnetic-Wave Excitation in GaAs/AlGaAs Heterostructures,” Physica E, Vol. 22, 2004, pp. 1-6. doi:10.1016/j.physe.2003.11.204
- R. R. Du, M. A. Zudov, C. L. Yang, Z. Q. Yuan, L. N. Pfeiffer and K. W. West, “Oscillatory and Vanishing Resistance States in Microwave Irradiated 2D Electron Systems,” In: Y. Wang, L. Engel and N. Bonesteel, Eds., High Magnetic Fields in Semiconductor Physics, World Scientific, Singapore, 2005, pp. 11-18. doi:10.1142/9789812701923_0001
- D. C. Tsui, H. L. Störmer and A. C. Gossard, “TwoDimensional Magnetotransport in the Extreme Quantum Limit,” Physical Review Letters, Vol. 48, 1982, pp. 1559- 1562. doi:10.1103/PhysRevLett.48.1559
- M. A. Zudov, R. R. Du, L. N. Pfeiffer and K. W. West, “Evidence for a New Dissipationless Effect in 2D Electronic Transport,” Physical Review Letters, Vol. 90, 2003, Article ID: 046807. doi:10.1103/PhysRevLett.90.046807
- R. G. Mani, V. Narayanamurti, K. von Klitzing, J. H. Smet, W. B. Johnson and V. Umansky, “Radiation-Induced Oscillatory Hall Effect in Highmobility GaAs/ AlxGa1 xAs Devices,” Physical Review B, Vol. 69, 2004, Article ID: 161306. doi:10.1103/PhysRevB.69.161306
- J. C. Phillips, “Microscopic Origin of Collective Exponentially Small Resistance States,” Solid State Communications, Vol. 127, No. 3, 2003, pp. 233-236. doi:10.1016/S0038-1098(03)00350-8
- A. V. Andreev, I. L. Aleiner and A. J. Millis, “Dynamical Symmetry Breaking as the Origin of the Zero-dc-Resistance State in an ac-Driven System,” Physical Review Letters, Vol. 91, No. 5, 2003, Article ID: 056803. doi:10.1103/PhysRevLett.91.056803
- A. C. Durst, S. Sachdev, N. Read and S. M. Girvin, “Radiation-Induced Magnetoresistance Oscillations in a 2D Electron Gas,” Physical Review Letters, Vol. 91, No. 8, 2003, Article ID: 086803. doi:10.1103/PhysRevLett.91.086803
- J. Shi and X. C. Xie, “Radiation-Induced Zero-Resistance State and the Photon-Assisted Transport,” Physical Review Letters, Vol. 91, No. 8, 2003, Article ID: 086801. doi:10.1103/PhysRevLett.91.086801
- F. S. Bergeret, B. Huckestein and A. F. Volkov, “CurrentVoltage Characteristics and the Zero-Resistance State in a Two-Dimensional Electron Gas,” Physical Review B, Vol. 67, 2003, Article ID: 241303. doi:10.1103/PhysRevB.67.241303
- S. Fujita, S. Godoy and D. Nguyen, “Bloch Electron Dynamics,” Foundation of Physics, Vol. 25, No. 8, 1995, pp. 1209-1220. doi:10.1007/BF02055258
- J. Bardeen, L. N. Cooper and J. R. Schrieffer, “Theory of Superconductivity,” Physical Review, Vol. 108, No. 5, 1957, pp. 1175-1204. doi:10.1103/PhysRev.108.1175
- S. Fujita, Y. Tamura and A. Suzuki, “Microscopic Theory of the Quantum Hall Effect,” Modern Physics Letters B, Vol. 15, No. 20, 2001, pp. 817-825. doi:10.1142/S0217984901002610
- R. B. Laughlin, “Anomalous Quantum Hall Effect: An Incompressible Quantum Fluid with Fractionally Charged Excitations,” Physical Review Letters, Vol. 50, No. 18, 1983, pp. 1395-1398. doi:10.1103/PhysRevLett.50.1395
- F. D. M. Haldane, “Fractional Quantization of the Hall Effect: A Hierarchy of Incompressible Quantum Fluid States,” Physical Review Letters, Vol. 51, No. 7, 1983, pp. 605-608. doi:10.1103/PhysRevLett.51.605
- J. K. Jain, “Composite-Fermion Approach for the Fractional Quantum Hall Effect,” Physical Review Letters, Vol. 63, No. 2, 1989, pp. 199-202. doi:10.1103/PhysRevLett.63.199
- J. K. Jain, “Incompressible Quantum Hall States,” Physical Review B, Vol. 40, No. 11, 1989, pp. 8079-8082. doi:10.1103/PhysRevB.40.8079
- J. K. Jain, “Theory of the Fractional Quantum Hall effect,” Physical Review B, Vol. 41, No. 11, 1990, pp. 7653- 7665. doi:10.1103/PhysRevB.41.7653
- R. E. Prange and S. M. Girvin, “The Quantum Hall Effect,” 2nd Edition, Springer-Verlag, New York, 1990.
- Z. F. Ezawa, “Quantum Hall Effects,” World Scientific, Singapore, 2000.
- M. Stone, “Quantum Hall Effect,” World Scientific, Singapore, 1992.
- T. Chakraborty and P. Pietilainen, “Quantum Hall Effects,” 2nd Edition, Springer-Verlag, Berlin, 1995. doi:10.1007/978-3-642-79319-6
NOTES
*Corresponding author.

