Journal of Modern Physics
Vol.3 No.1(2012), Article ID:17103,5 pages DOI:10.4236/jmp.2012.31006
Symmetry Violation of Time Reversal in Third Order Vertex Angle Renormalization Process of Electromagnetic Interaction
Department of Physics, Institute of Innovative Physics, Fuzhou University, Fuzhou, China
Email: ycwlyjs@yeah.net
Received November 11, 2011; revised December 18, 2011; accepted December 29, 2011
Keywords: Quantum theory of field; Symmetry; Time reversal; T Violations; Normalization; Vertex Angle Process
ABSTRACT
According to the current understanding, electromagnetic interaction is invariable under time reversal. However, the proof of time reversal symmetry in quantum theory of field has not considered the effects of high order perturbation normalizations. It is proved in the paper that when the renormalization effect of third order vertex angles process is taken into account, the symmetry of time reversal will be violated in electromagnetic interaction process. Because the magnitude order of symmetry violation is about 10–5, but the precision of current experiments on time reversal in particle physics is about 10–3, this kind of symmetry violation can not be found. The result reveals the micro-origin of asymmetry of time reversal and can be used to solve the famous irreversibility paradox in the evolution processes of macromaterial systems.
1. Introduction
According to the current understanding, the electromagnetic interaction processes of micro-particles are symmetric under time reversal, for the motion equation of quantum mechanics and the interaction Hamiltonian of electromagnetic interaction are considered invariable under time reversal. On the other hand, as we know that the evolution processes of macro-material systems which obey the second law of thermodynamics always violate time reversal symmetry. Therefore, there exists a famous and unsolved contradiction, i.e., the so-called irreversibility paradox. Because macro-systems are composed of atoms and molecules, and atoms and molecules are composed of charged particles. By logical deductions, electromagnetic interaction between micro-particles should contain certain asymmetry under time reversal. We had to ask whether or not our current understanding on electromagnetic interaction has some basic mistake.
In fact, dissipation and irreversibility exist commonly in practical electromagnetic phenomenon. A most typical example is the heat effect of resistance in circuitry. Another example is laser, related to electromagnetic interaction, which is strong non-equilibrium process with high irreversibility. In addition, most non-linear optical processes, just as the optical sum frequency, double frequency and different frequency, double stable states, selffocusing and self-defocusing, echo phenomena, as well as optical self-transparence and self observations and so on [1], are obviously violate time reversal symmetry. The problem is that the current theory of electromagnetic interaction is considered symmetrical under time reversal, so that though physicists look at these phenomena, they can not see symmetry violations at present.
The affirmation that electromagnetic interaction is symmetric under time reversal has seriously hampered our correct understanding on the character of microcosm. The experiment is the first in physics. The theory should obey experiments and facts. Because symmetry violation of time reversal exists practically in the processes of electromagnetic interaction, we should tray to explain it in theory, in stead of evading it.
In fact, the author has completed a series of works in this field. It is proved that when the electromagnetic retarded interaction is taken into account in quantum mechanics, the light’s high order stimulated radiation and absorption processes violate time reversal symmetry [2], though the total interaction Hamiltonian is still unchanged under time reversal in the processes. Based on it, the basic theory of laser physics and the polarization formula of non-linear optics are revised so that they become irreversibility under time reversal [3]. In this way, a more rational foundation is established for the theories.
In this paper, we discuss symmetry violation of time reversal in quantum theory of field further. The experiments show that there is no symmetry violation of time reversal in the low order processes of electromagnetic interaction. We will prove that when renormalization effect is considered, the third order vertex angles processes of electromagnetic interaction violate time reversal symmetry. The situation is similar to that the regularizations of some high order processes cause chirality’s anomalies and violates gauge invariability in the gauge theory of field [4]. Because symmetry violation is very small with the magnitude order about 10–5, but the experiment precision to test time reversal symmetry in current particle physics was about 10–3, the experiments could not find them.
The results indicate that no matter in quantum mechanics or in quantum theory of field, electromagnetic interactions violate time reversal symmetry generally. The difference is that in quantum mechanics, we discuss electromagnetic interactions between charged particles of bounding states in atoms and molecules. Symmetry violation of time reversal occurs in the second processes with big magnitude order. But in quantum theory of field, we discuss electromagnetic interactions between charged particles of non-bounding states and photons. Symmetry violations occur in the third order processes with mall magnitude order.
The results reveal the common existence of time reversal asymmetry in microcosm which can be used to solve the famous irreversibility paradox in the evolution processes of macro-material systems. That is to say, the irreversibility of macro-processes originates from the irreversibility of micro-processes in essence.
2. Time Reversals of Physical Quantities in Momentum Space
In quantum theory of field, the time reversals of electromagnetic field 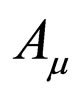 and spinor field
and spinor field 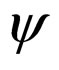 in the coordinate space are defined as individually [5]
in the coordinate space are defined as individually [5]
 (1)
(1)
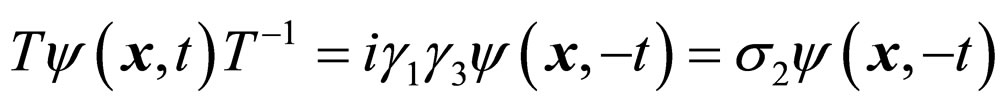 (2)
(2)
 . (3)
. (3)
Here T is time reversal operator and 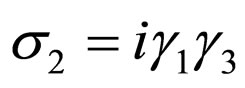 is the Pauli matrix. The Hamiltonian of electromagnetic interaction is defined as
is the Pauli matrix. The Hamiltonian of electromagnetic interaction is defined as
ℋ
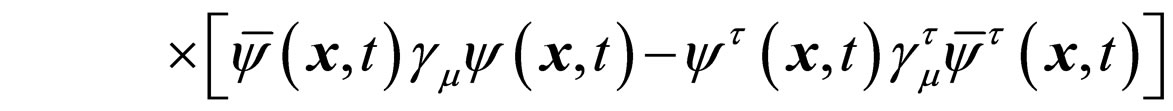 (4)
(4)
The time reversal of (4) is carried out according to following procedure. Because T is anti-unitary operator, we have 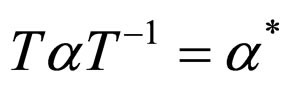 and
and . By considering relations
. By considering relations 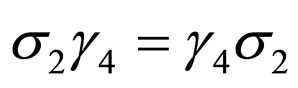 and
and 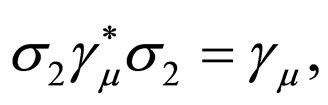 we have [5]
we have [5]
Tℋ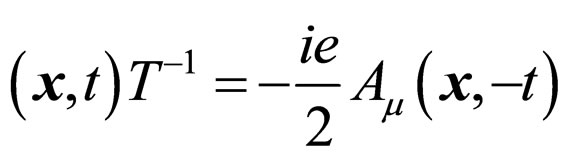
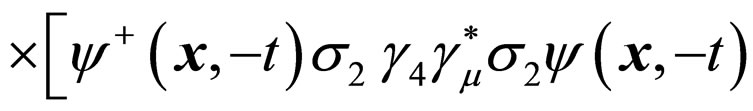
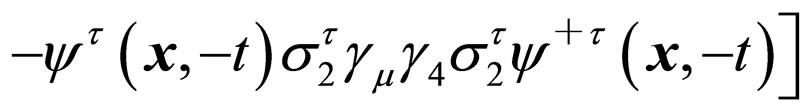
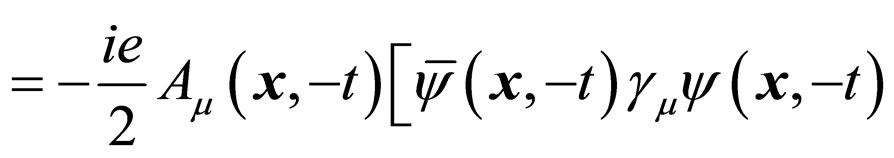
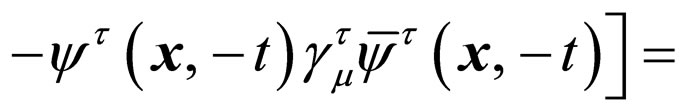 ℋ
ℋ (5)
(5)
According to quantum theory of field, the results are the same when we use both ℋ and ℋ
and ℋ to calculate the transition probabilities of concrete problems. In this meaning, we say that electromagnetic interaction is symmetric unchanged under time reversal.
to calculate the transition probabilities of concrete problems. In this meaning, we say that electromagnetic interaction is symmetric unchanged under time reversal.
It should be emphasized that the Formula (4) does not contain the normalization effects of high order perturbation processes. We will prove below that if the renormalization effects are considered, the third order vertex angle process violates time reversal symmetry.
The Formulas (1)-(5) are described in the coordinate space, but the concrete problems are calculated in the momentum space in quantum theory of field. We need to know the time reversals of physical quantities in the momentum space. The quantized spinor field in the coordinate space is
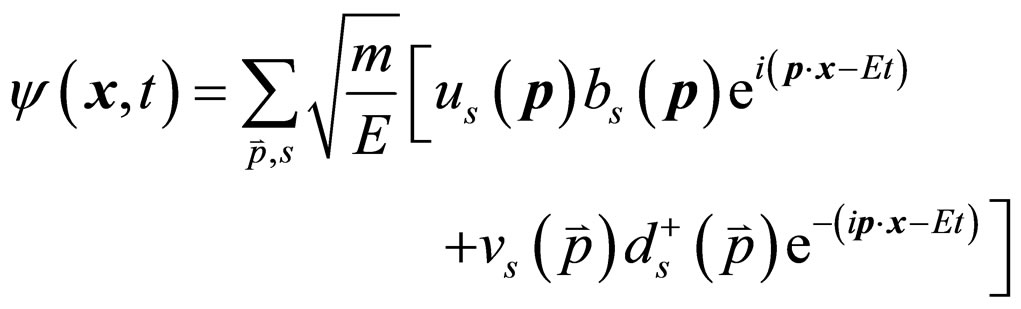 (6)
(6)
We have known following relations [5]
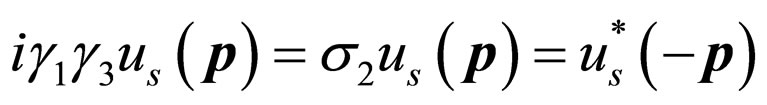
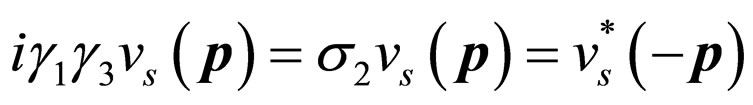 (7)
(7)
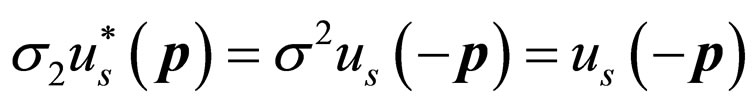
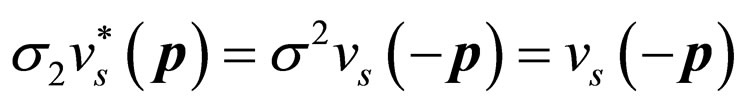 (8)
(8)
By the relations above, we can get the time reversals of creation and annihilation operators [5]
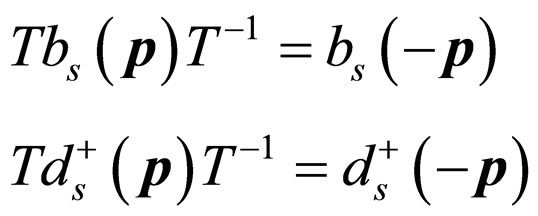 (9)
(9)
as well as the time reversals of spinor fields in the momentum space
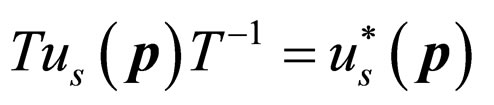
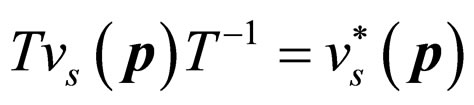 (10)
(10)

 (11)
(11)
For the convenience of calculation, we define matrixes 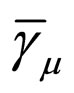 and
and 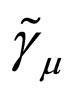 as
as
 (12)
(12)
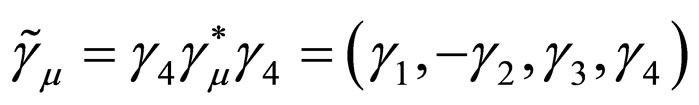
 (13)
(13)
It is obvious that 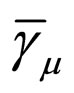 and
and 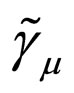 are also the Hermitian matrixes with the same communicate relations
are also the Hermitian matrixes with the same communicate relations
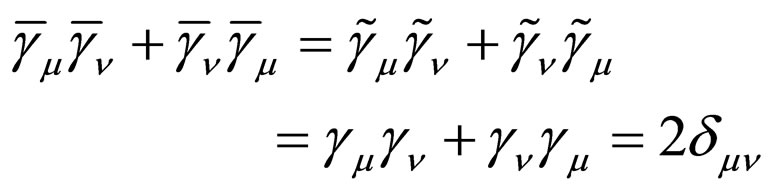 (14)
(14)
Meanwhile, we write the four dimensional momentum quantities as
 (15)
(15)
with
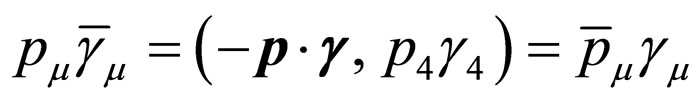 (16)
(16)
The formulas are useful in the following calculations.
3. T Violation in the Renormalization Processes of Third Order Vertex Angles
We now discuss the time reversal of a single third order vertex angle process when the renormalization effect is considered. We calculate the process that an electron is scattered by the external electromagnetic field. By omitting the invariable factor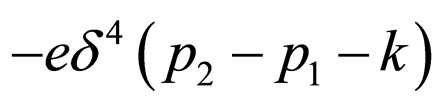 , the total probability amplitudes of the first and third order processes can be written as [6]
, the total probability amplitudes of the first and third order processes can be written as [6]
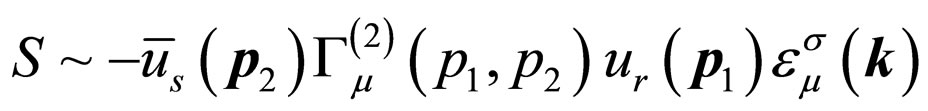 (17)
(17)
Here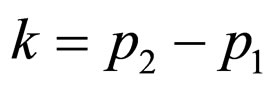 . In general situations, (17) can be considered as a part of more complex Feynman diagram. If regularization and renormalization are not considered, (17) is symmetric under time reversal. After regularization is carried out and infinite is separated, we get
. In general situations, (17) can be considered as a part of more complex Feynman diagram. If regularization and renormalization are not considered, (17) is symmetric under time reversal. After regularization is carried out and infinite is separated, we get
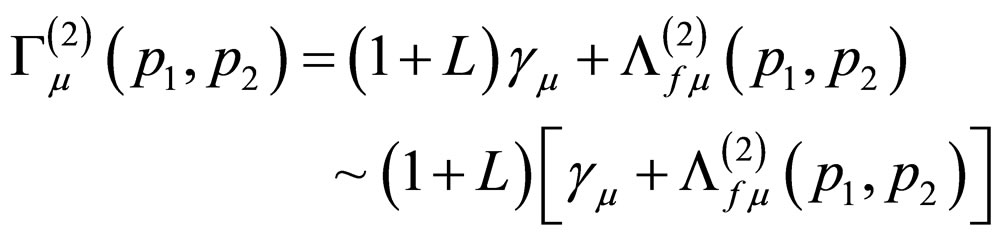 (18)
(18)
in which L is infinite, 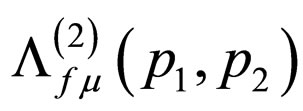 does not contain ultraviolet divergence but contains infrared divergence. In order to eliminate infrared divergence, we suppose that photon has a small static mass
does not contain ultraviolet divergence but contains infrared divergence. In order to eliminate infrared divergence, we suppose that photon has a small static mass  at first, and let
at first, and let 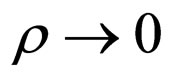 at last according in the current calculation [6]. By means of the procedure of charge renormalization to let
at last according in the current calculation [6]. By means of the procedure of charge renormalization to let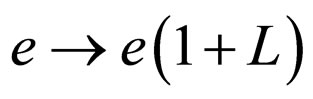 , we obtain finite probability amplitude
, we obtain finite probability amplitude
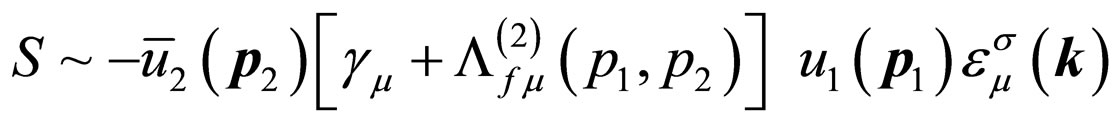 (19)
(19)
in which
 (20)
(20)
 (21)
(21)
 (22)
(22)
 (23)
(23)
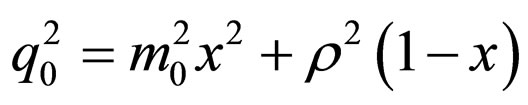
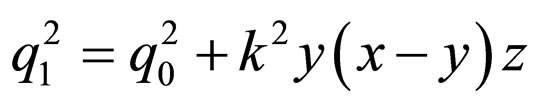 (24)
(24)
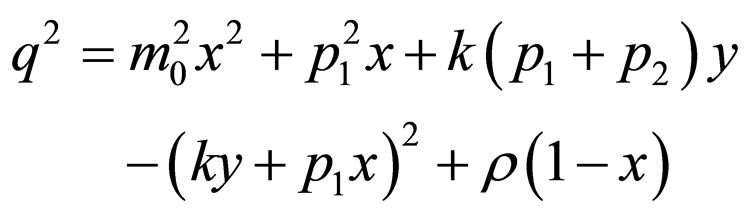 (25)
(25)
Let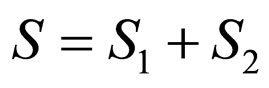 , we have
, we have
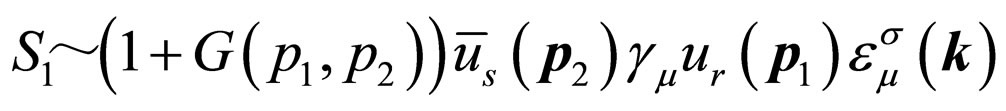 (26)
(26)
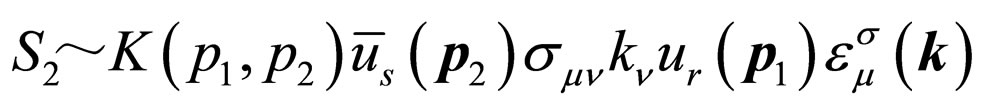 (27)
(27)
According to the definition, we have ,
, 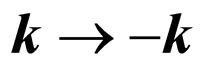 ,
, 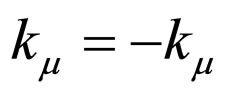 and
and 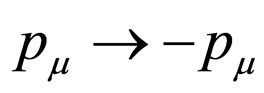 under time reversal. Therefore,
under time reversal. Therefore, 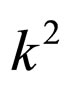 ,
, 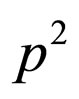 and
and 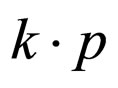 are invariable. The functions
are invariable. The functions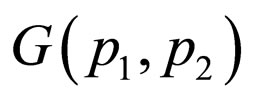 and
and 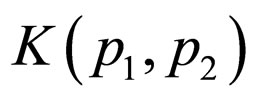 are also unchanged under time reversal. By inserting factor
are also unchanged under time reversal. By inserting factor 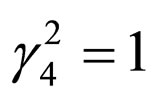 in (26), we have the time reversal of
in (26), we have the time reversal of 
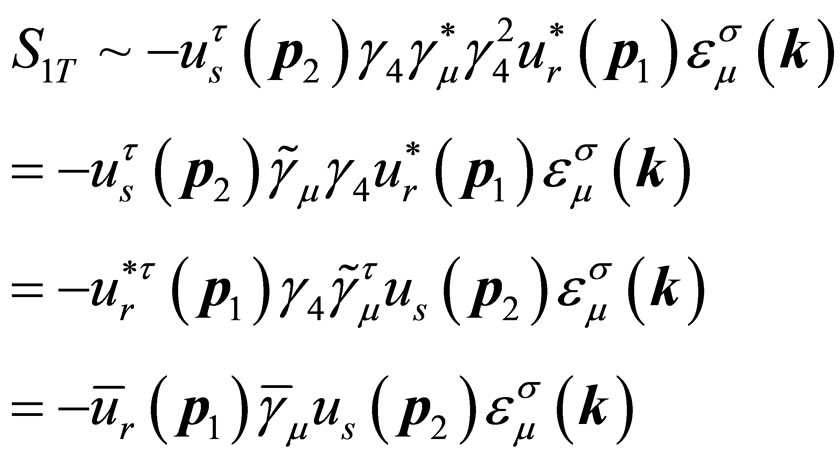 (28)
(28)
On the other hand, by taking the complex conjugation of (26) and (28) and considering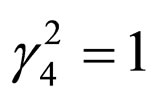 , we get
, we get
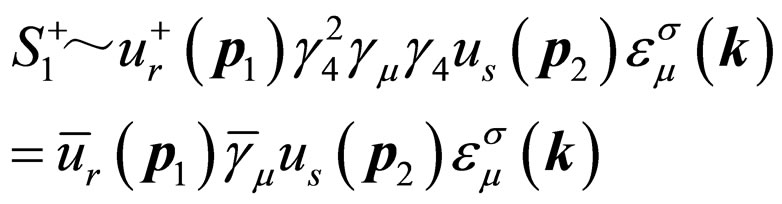 (29)
(29)
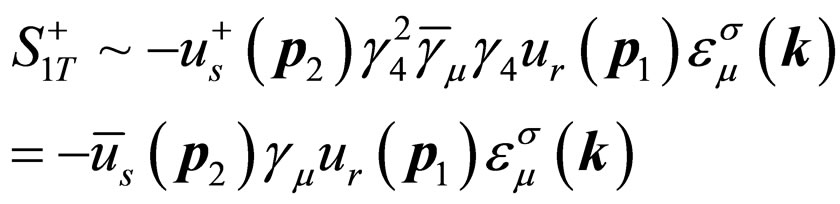 (30)
(30)
So we have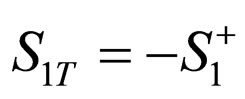 ,
, 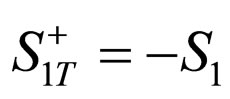 ,
,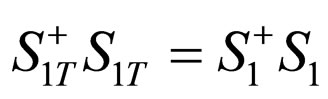 . Then let’s consider the time reversal of
. Then let’s consider the time reversal of . By using (12) and (13), we have
. By using (12) and (13), we have
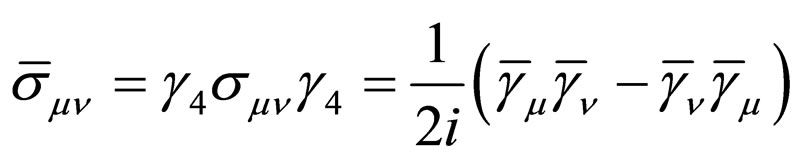
 (31)
(31)
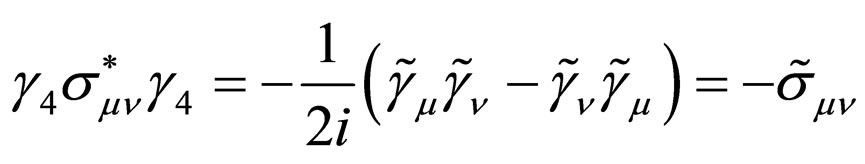 (32)
(32)
 (33)
(33)
Then, the time reversal of 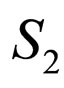 is
is
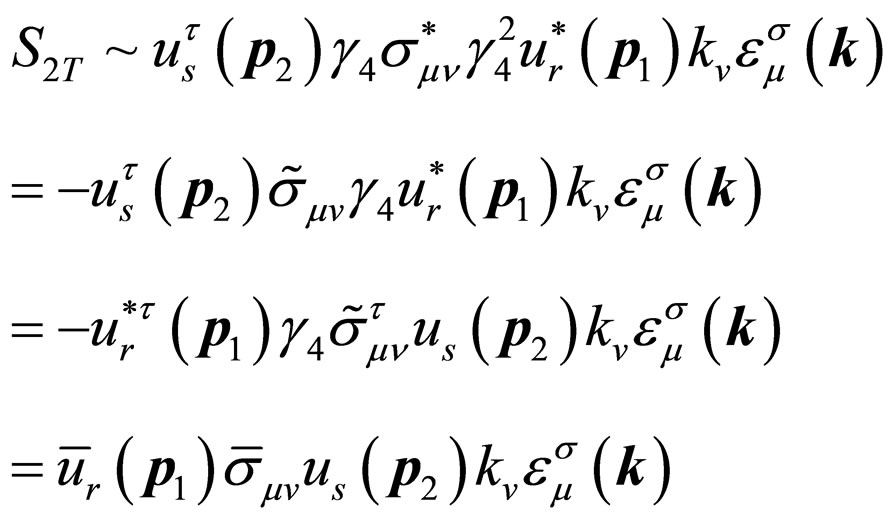 (34)
(34)
It is easy to prove that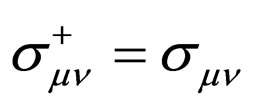 ,
,  and
and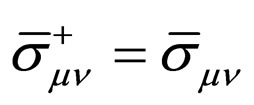 . So by taking the complex conjugations of
. So by taking the complex conjugations of  and
and , we obtain
, we obtain
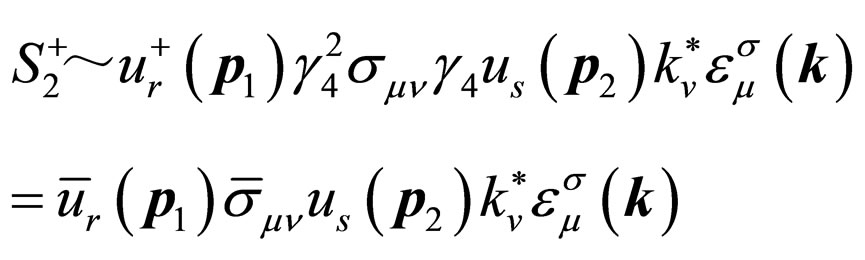 (35)
(35)
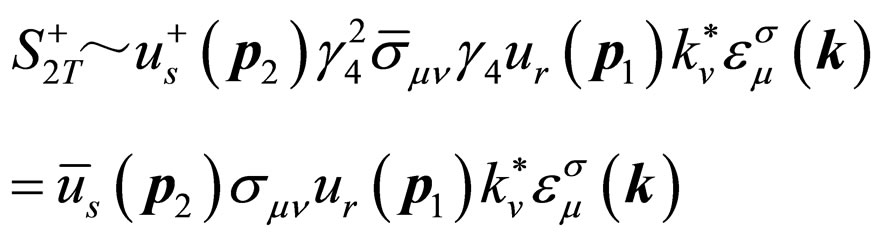 (36)
(36)
Because of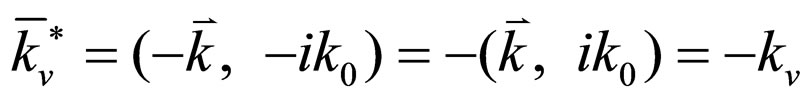 , we have at last
, we have at last
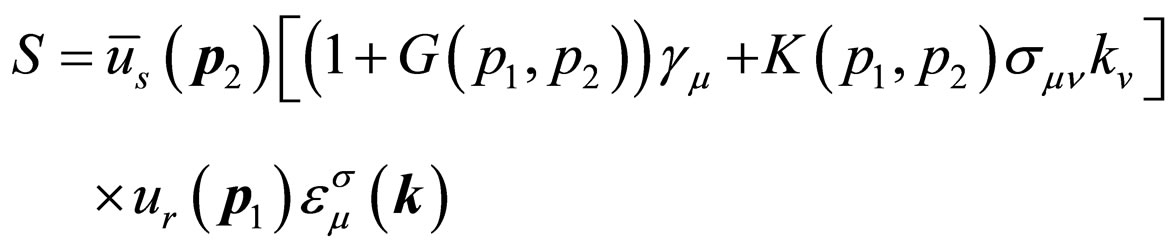 (37)
(37)
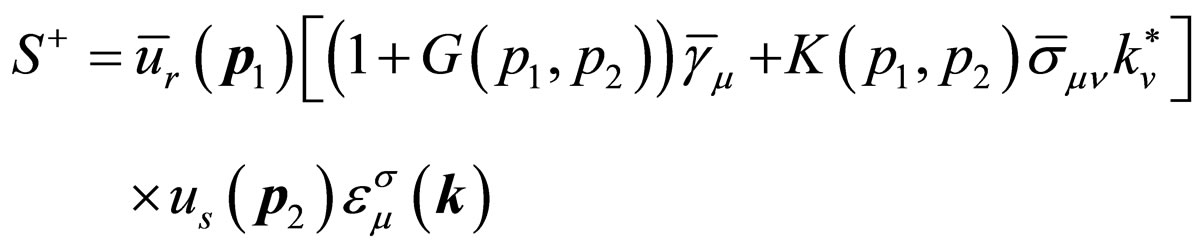 (38)
(38)
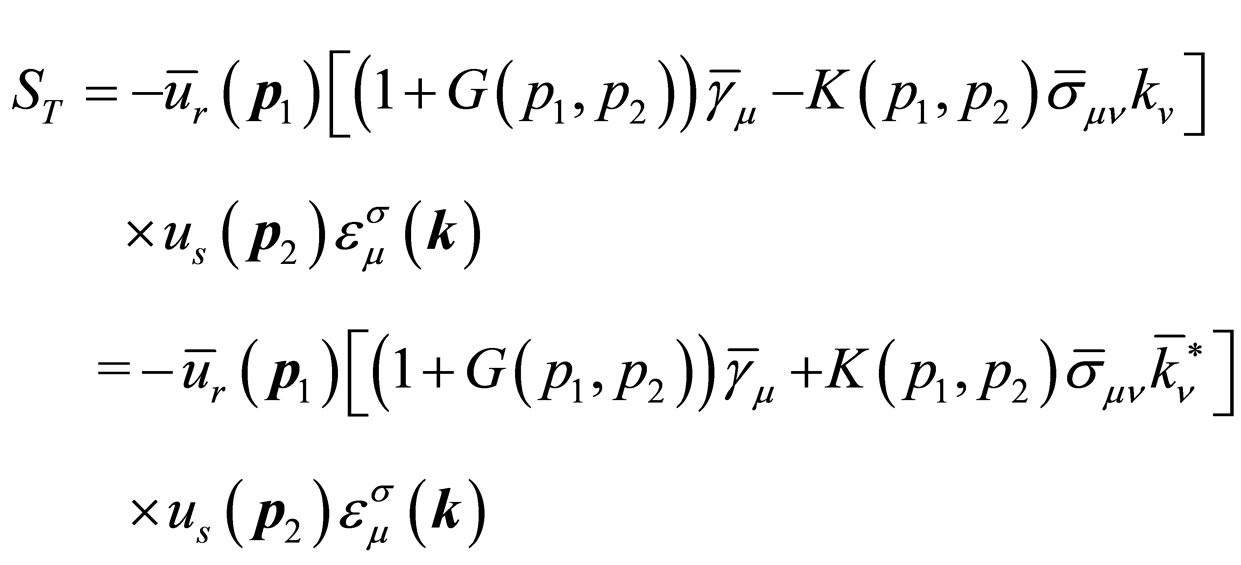 (39)
(39)
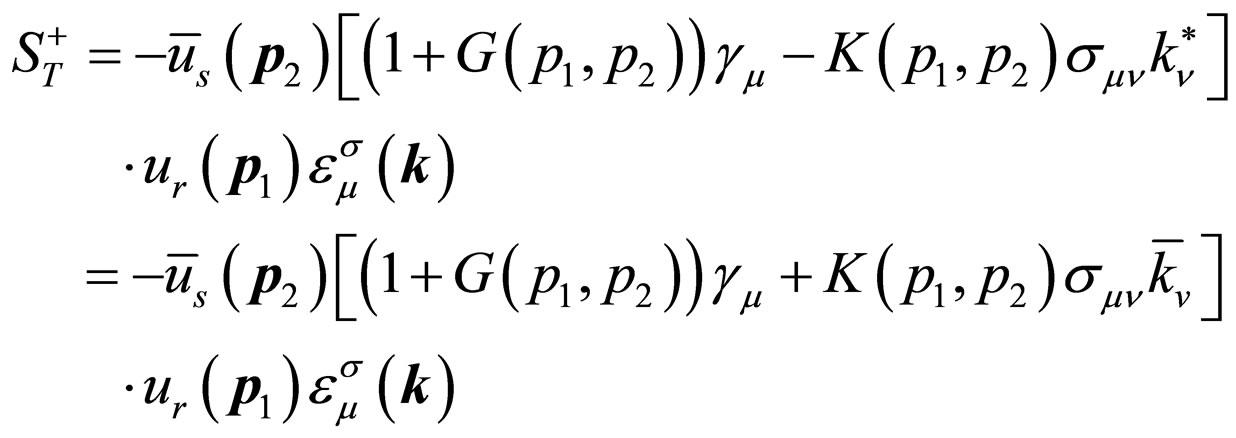 (40)
(40)
Comparing the formulas above, we know that to let 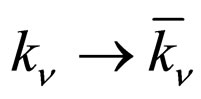 (or
(or ) in S, we obtain
) in S, we obtain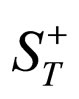 . To let
. To let 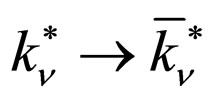 (equal to
(equal to 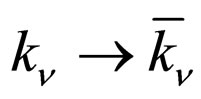 or
or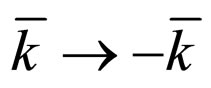 ) in S+, we obtain
) in S+, we obtain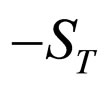 . That is to say, to let
. That is to say, to let 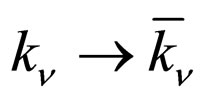 in
in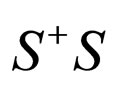 , we obtain
, we obtain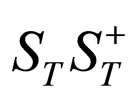 . However, it is obvious that when
. However, it is obvious that when 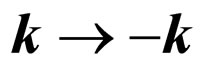 we have
we have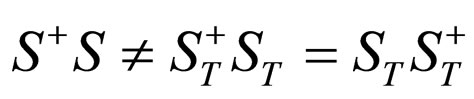 . The result indicates that the transition probability violates time reversal symmetry when the renormalization effect of the third order vertex angle process is considered.
. The result indicates that the transition probability violates time reversal symmetry when the renormalization effect of the third order vertex angle process is considered.
We can prove that the total transition probability of the renormalization processes of all third order vertex angles in the coordinate space also violates time reversal symmetry. We have equivalent relations

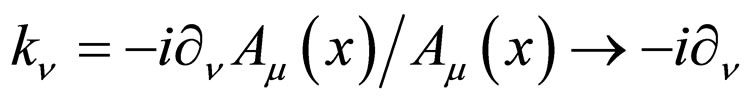 (41)
(41)
So we can equally write the total probability amplitude of all third order vertex angle processes as
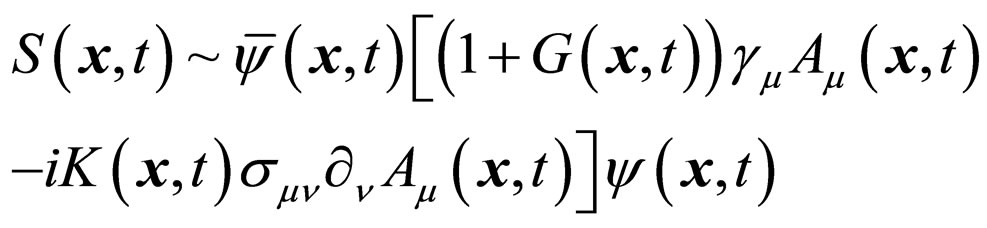 (42)
(42)
The Formula (42) contains four processes actually. They are the scattering between electron and electron described by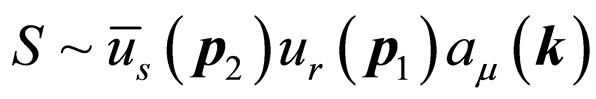 , the scattering between positive electrons described by
, the scattering between positive electrons described by 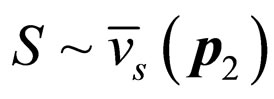
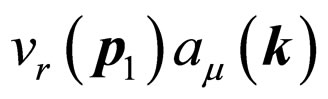 , as well as the generation and annihilation processes of electron and positive electron described by
, as well as the generation and annihilation processes of electron and positive electron described by 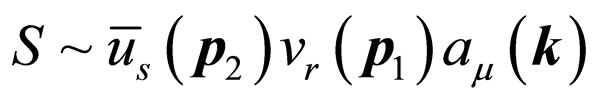 and
and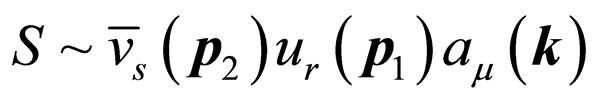 . The operator
. The operator 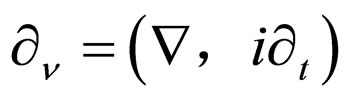 is unchanged under time reversal. And so do for the time reversal of functions with
is unchanged under time reversal. And so do for the time reversal of functions with 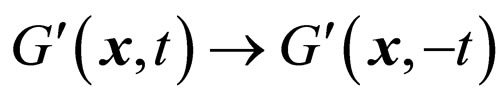 and
and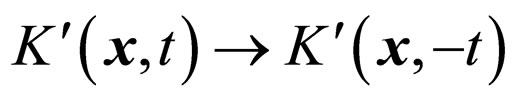 . By considering
. By considering 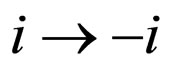 and
and 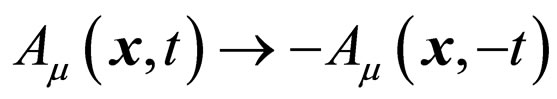 under time reversal, as well as the relation
under time reversal, as well as the relation  and
and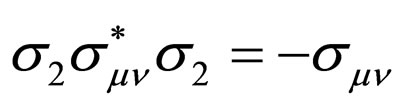 , we have the time reversal of (42)
, we have the time reversal of (42)
 (43)
(43)
On the other hand, if let 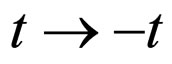 in (42) and take
in (42) and take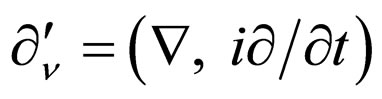 , we have
, we have
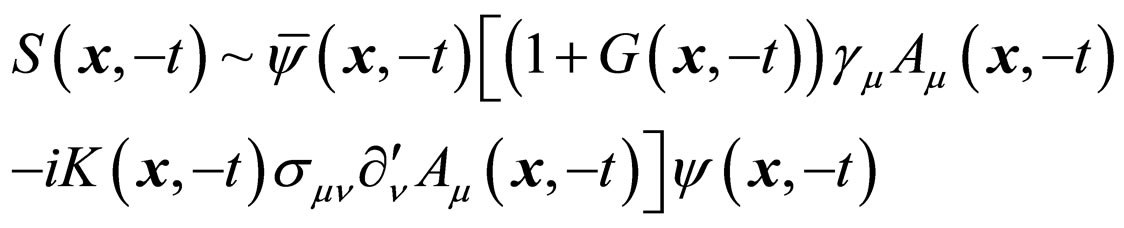 (44)
(44)
Because of 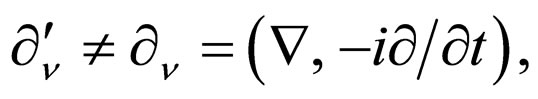 we have
we have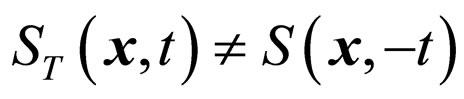 . According to (5), the interaction Hamiltonian in the coordinate space is invariable under time reversal. We should have
. According to (5), the interaction Hamiltonian in the coordinate space is invariable under time reversal. We should have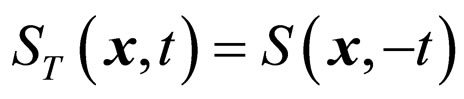 . Because the condition is not satisfied, (43) violates the symmetry of time reversal. Therefore, no matter in the momentum space or in the coordinate space and no matter for a single process or for the sum of all processes, the renormalizations of third order vertex angles violate time reversal symmetry in electromagnetic interaction processes.
. Because the condition is not satisfied, (43) violates the symmetry of time reversal. Therefore, no matter in the momentum space or in the coordinate space and no matter for a single process or for the sum of all processes, the renormalizations of third order vertex angles violate time reversal symmetry in electromagnetic interaction processes.
Because vertex angles are the elements of the Feynman diagrams, so the high order processes of electromagnetic interaction in quantum theory of field violate time reversal symmetry commonly. But the symmetry violations in high order processes are very small with magnitude order about 10–5. The current experiments precision on time reversal is about 10–3, so that this symmetry violation appearing in the renormalization processes of quantum theory of field has not been found at present day.
4. CPT Symmetry Violations in High Order Renormalization Processes
It is easy to prove that the renormalizations of third order vertex angle processes are symmetric under P and C transformations in electromagnetic interactions. Due to the symmetry violation of time reversal, the renormalization processes violate  symmetry in electromagnetic interactions. It is easy to prove that this kind of
symmetry in electromagnetic interactions. It is easy to prove that this kind of  symmetry violation does not affect the static masses of positive and anti-particles. Let ℋ0
symmetry violation does not affect the static masses of positive and anti-particles. Let ℋ0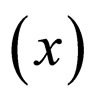 represent the Hamiltonian operator of particle’s static energy (or static mass),
represent the Hamiltonian operator of particle’s static energy (or static mass), 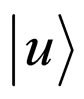 represent the state of positive particle and
represent the state of positive particle and 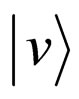 represent the state of anti-particle. Because the operator of static energy ℋ0
represent the state of anti-particle. Because the operator of static energy ℋ0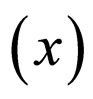 does not contain the revision of high order renormalization, we also have
does not contain the revision of high order renormalization, we also have
CPTℋ0 ℋ0
ℋ0 (45)
(45)
So under CPT transformation, we also have
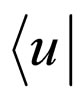 ℋ0
ℋ0
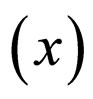 ℋ0
ℋ0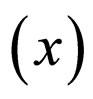
 ℋ0
ℋ0
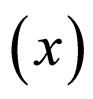 (46)
(46)
That is to say, positive and anti-particles still have the same static energy (static mass). The symmetry violation of united CPT transformation is insensitive to the static mass of positive and anti-particles. We still have same static mass for positive and anti-particles. The magnitude order of CPT violation is very small. The reason of CPT violation keeps to later discussion.
REFERENCES
- Y. R. Shen, “The Principles of Nonlinear Optics,” WileyInterscience, New York, 1984.
- X. C. Mei, “Electromagnetic Retarded Interaction and Symmetry Violation of Time Reversal in Light’s High Order Stimulated Radiation and Absorption Processes,” Science in China Series G: Physics, Mechanics & Astronomy, Vol. 51, No. 3, 2008, pp. 282-298.
- X. C. Mei, “Electromagnetic Radiation, Retarded Electromagnetic Interaction and Symmetry Violation of Time Reversal in Nonlinear Optic Processes—Influence on Fundamental Theory of Laser and Non-Equivalent Statistical Physics,” Electromagnetic Radiation, InTech Open Access, 2012.
- Y. B. Dai, “The Gauge Theory of Interaction,” Science Publishing Company, 2005.
- T. D. Lee, “Particle Physics and Introduction to Field Theory,” Harwood Academic Publishers, Harwood, 1981.
- H. Y. Zhu, “The Quantum Theory of Fields,” Science Publishing Company, 1960.

