Journal of Modern Physics
Vol.2 No.12(2011), Article ID:9035,17 pages DOI:10.4236/jmp.2011.212181
Dark Energy as a Property of Dark Matter
independent author, San Jose, USA
E-mail: jacquesleibovitz@berkeley.edu
Received July 10, 2011; revised September 11, 2011; accepted Octobers 8, 2011
Keywords: dark energy, dark matter
ABSTRACT
A novel model of dark matter (DM), elastically compressible, can contribute to the acceleration of our Universe expansion. While each galaxy compresses its own DM within its gravitation field, the DM bordering neighboring galaxies, far from their centers, is pulled apart. It is shown that, although the DM pressure tends to zero at such locations, the DM compressibility tends to infinity. This allows the DM to expand between galaxies without gravitation hindrance. The model is consistent with the coupled distributions of baryonic and dark matters, with black hole formation at the centers of large galaxies, with galactic flat rotation curves, with a Tully-Fisher relation, and with Milgrom’s MOND relation. Results are discussed.
1. Introduction
A main problem in astrophysics is the discovery, about two decades ago, that our Universe expansion is accelerating, instead of slowing down as predicted by the Big Bang theory [1] Scientists hypothesize the existence of an anti-gravity energy field dubbed Dark Energy (DE). It has been claimed that the identification and understanding of that DE would be the greatest accomplishment of the century [2].
A less recognized problem is the Big Bang itself, the explosion of the biggest of black holes, which the present theory and model of black holes cannot accommodate. Instead, the Big Bang theory deals with the evolution of our Universe after the initial Bang [1]. Inclusion of the DE proposed here could destabilize black holes sufficiently to help resolve that problem.
An elastically compressible DM might contribute to the accelerated expansion of our Universe and to the destabilization of black holes. In the following, we show that such model of DM is consistent with the observed DM phenomena. Then, we derive a possible mechanism of acceleration of our Universe expansion.
1.1. Dark Matter or New Physics?
The prevailing scientific view today is that DM is constituted of weakly interacting massive particles (WIMPs). At this time, such view must be considered a hypothesis because, so far, a constitutive particle of DM has not been detected, and computer simulations based on the predicted microscopic properties of WIMPs have not succeeded in modeling the observed behavior of DM [1-15].
An alternative hypothesis is that DM is not a substance at all and that the DM-phenomena result from a “new physics.” Some scientists proposed a modification of Newton dynamics (MOND) for weak acceleration as such alternative [16-23]. Milgrom’s version of MOND [16-22] proposes at very low accelerations, corresponding to very large distances R, a relation that departs from Newton laws as follows: defining γo as a small constant (= about 10−8 cm·s−2) of acceleration dimensions, then for γ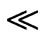 γo MOND departs from Newton laws by postulating:
γo MOND departs from Newton laws by postulating:
γsmall = F/M = − (GMγo)1/2R−1 = −(Vc)2R−1. (1.1.1)
From equation (1.1.1):
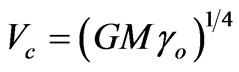 , (1.1.2)
, (1.1.2)
at very low accelerations, corresponding to very large distances Rlarge.
Although MOND’s relation does not define the dynamics in the intermediate range where γ ≈ γo, it is tailored to produce the galactic rotation curve plateau in a form (equation (1.1.2)) fitting a Tully-Fisher relation (TFR). However, MOND relates the luminous mass of the galaxy with the limiting speed (equation (1.1.2)) while the TFR implies a relation with the maximum, or peak speed.
While very successful at modeling much of DM behavior, serious reasons preclude the scientific acceptance of MOND [16-21,24,25]. In particular, Milgrom’s derivation of MOND, based on a departure from Newton laws of gravitation, though speeds are small compared with the speed of light, conflicts with general relativity and makes that derivation unacceptable. However, because some doubt that DM particles will be substantiated, it has been suggested to take a new look at MOND [26]. On the other hand, the recent observation of dissociation between DM and baryonic clouds during a collision of galactic clusters [27] tends to tip the scales, at this time, in favor of the existence of DM.
Here, we explore another “new physics” consisting of an elastically compressible DM, with a mass density distribution ρ. The exploration of such “new physics” appears fruitful, leading to the derivation of an equation of state (EoS) for such DM in a gravitation field, of an equation governing the coupled distributions of baryonic and dark matters around galaxies, of a possible mechanism of black hole formation at the centers of large galaxies, of galactic flat rotation curves, of a Tully-Fisher relation, of Milgrom’s MOND relation, and of a possible mechanism for the accelerated expansion of our universe.
1.2. Alternative Model of Dark Matter
a) DM is a non-baryonic substance, consistent with the observation of a collision between galactic clusters [27].
b) DM distribution is spherically symmetric around some spiral galaxies, without flattening at the poles [3, 6,10,28].
c) Consistent with assumption (b), DM does not necessarily partake in galaxy rotation [1,3,4,10,28]. The concept that DM is constituted of particles conflicts with this assumption.
d) Dark matter has no centrifugal force to balance the centripetal gravitation pull, consistent with assumption (c).
e) Instead, we assume that DM is elastically compressible, without energy dissipation, and develops a DM-pressure P, which balances the gravitation pull on DM.
Because DM-WIMPs have no self interaction sufficient to develop DM-pressure high enough to balance the gravitation pull, assumption (e) excludes the possibility that DM be constituted of WIMPs, consistent also with the absence of success, so far, of efforts to prove the existence of DM-WIMPs [1-4,7,8,11-15].
f) Newton dynamics may be used as a good approximation of general relativity in the limits of speeds small relative to the speed of light and of weak gravitation.
2. Coupled Distributions of Baryonic and Dark Matters
To simplify, we consider only systems of spherical symmetry.
Including DM mass, Newton’s equations applied to a spherically symmetric galaxy yield:
F = −G(M + m)M'R−2 (2.1)
where M and m (g) are the baryonic (mostly luminous) mass and the DM-mass, respectively, both within a radius R from the galaxy center, and F is the gravitation force applied by the sum of M and m on a gravitating small test mass M' at radial distance R from the galaxy center.
The gravitational acceleration γ of M' at R then is:
γ = −(Vc)2/R = F/M' = −G(M + m)R−2, (2.2)
from which:
(Vc)2 = −G(M + m)R−1 (2.3)
and Vc = [G(M + m)R−1]1/2. (2.4)
The mass m may be expressed as:
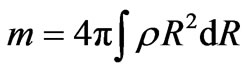 (2.5)
(2.5)
from which:
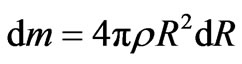 (2.6)
(2.6)
where ρ is the DM density at location R.
2.1. Equation of State of Dark Matter in a Gravitation Field
Staying with the simplicity of spherical symmetry, let us consider a spherically symmetric distribution of baryonic mass, its associated DM, and their gravitation field of center O, at infinite distance from any other mass.
Because DM does not necessarily rotate around galaxies (assumption c), it lacks the centrifugal force that might balance the gravitation force on DM (assumption d). Instead, the gravitational field elastically compresses DM to a pressure distribution P (g·cm−1·s−2), function of radial distance R, without energy dissipation (assumption e). Therefore, the pressure P is a function only of location R and of other functions of R. The DM pressure balances the gravitation force and may be expressed in differential form as the ratio of the gravitation differential force dFm exerted by the sum of M and m on the differential mass dm of the DM confined in a spherical shell of radius R, and differential thickness dR, to the surface area S (= 4πR2) of that shell:
dP = −G(M + m)R−2dm(4π)−1R−2= γ(4π)−1R−2dm = ρdR < 0, (2.1.1)
in which Equation (2.6) was used in the last step.
Equation (2.1.1) shows that the pressure P is expressible in terms of the location R, the DM mass density ρ at location R, and the gravitation acceleration γ (of a test mass M') at that location. The pressure might be expressed as:
P – Poo = −AργR = Aρ(Vc) (2.1.2)
where Poo is the DM pressure at infinite distance, and A is a dimensionless constant. When the value of A is determined, equation (2.1.2) provides the EoS for DM in the spherically symmetric gravitation field.
To determine the value of the integration constant A, we derive an expression for the distribution of DM mass-density ρ around a galaxy and then compare it to the boundary condition at very large radii Rlarge. The procedure is as follows:
Form the ratio of equation (2.1.1) to equation (2.1.2), side by side:
 (2.1.3)
(2.1.3)
and by integration:
Log(P – Poo) + A−1Log (R) = Log(constant) (2.1.4)
or:
(P – Poo)R(1/A) = –AργR[1+(1/A)] = Aρ(Vc)2R(1/A) = constant = Ak (2.1.5)
where the integration constant is conveniently written as Ak to yield:
–ργR[1+(1/A)] = ρ(Vc)2R(1/A) = k, another constant speci-fic to the galaxy. (2.1.6)
The constant k is specific to the galaxy because it is a function of the total luminous mass M and of its distribution in the galaxy, so that 2 galaxies of equal total luminous mass but with different distributions can have different constants k.
For a galactic flat rotation curve, Vc becomes constant at very large radial distances Rlarge, which requires that the DM mass density be distributed there as:
ρ(Rlarge)2 = K, another constant specific to the galaxy.
(2.1.7)
From equation (2.1.6):
ρR(1/A) = k/(Vc)2. (2.1.8)
Equation (2.1.8) shows that the necessary and sufficient condition for Vc to remain constant in any range of radial locations R, is that ρR(1/A) remain constant in that range. Comparison with equation (2.1.7), shows that equation (2.1.8) has the required form, and that the constant A = 1/2.
With the determination of A = 1/2, equation (2.1.2) becomes the sought EoS:
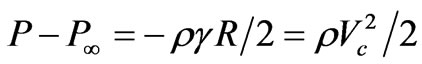 . (2.1.9)
. (2.1.9)
Because of the restriction to spherical symmetry, equation (2.1.9) is the EoS derived for DM outside any galaxy and inside any spherically symmetric galaxy, except perhaps at sufficiently high DM-pressures where DM might undergo phase changes with corresponding changes of properties. Such changes might occur sufficiently close to some galaxy centers.
However, being a material property of DM, the validity of the EoS (equation 2.1.9) is not limited to spherical symmetry and would be valid outside and inside any galaxy, except perhaps at sufficiently high DM pressures where DM might undergo phase changes with corresponding changes of DM properties. Such changes might occur sufficiently close to some galaxy centers.
2.2. Equation Governing the Coupled Distributions of Baryonic and of Dark Matter
With the determination of the constant A = 1/2, equation (2.1.8) becomes:
–ργR3 = ρ(Vc)2R2 = k. (2.2.1)
Because Vc depends on the distribution of both the baryonic mass and the DM mass, its participation in equation (2.2.1) means that this equation (2.2.1) governs both distributions.
Equation (2.2.1) satisfies the known trivial condition that for Vc to become constant at sufficiently large distances Rlarge, the expression 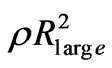 must become constant there (equation (2.1.7)).
must become constant there (equation (2.1.7)).
Still, it remains to show that both Vc and 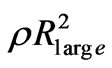 do become constant at sufficiently large distances Rlarge. We now derive that result and, therefore, the flat galactic rotation curves.
do become constant at sufficiently large distances Rlarge. We now derive that result and, therefore, the flat galactic rotation curves.
2.3. Derivation of Galactic Flat Rotation Curves
Combine equations (2.2 and 2.5) and rearrange to yield:
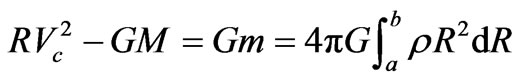 . (2.3.1)
. (2.3.1)
The validity of equation (2.3.1) is restricted to spherical symmetry.
Form the differential on both sides of equation (2.3.1), to obtain:
(Vc)2dR + Rd(Vc)2 – GdM = 4πGρR2dR. (2.3.2)
Substitute for  from equation (2.2.1) to yield:
from equation (2.2.1) to yield:
(Vc)2dR + Rd(Vc)2 – GdM = 4πGk[dR/(Vc)2]. (2.3.3)
Express dM in terms of the luminous mass density ρb:
dM = 4πρbR2dR. (2.3.4)
Substitute into equation (2.3.3), multiply throughout by (Vc)2/R, and re-arrange to yield:
(Vc)4dR/R + (Vc)2d(Vc)2 – G4πρb(Vc)2RdR = 4πGk[dR/R].
or:
G4πk(ρb/ρ)dR/R + 4πGk[dR/R] – (Vc)4dR/R – (Vc)2d(Vc)2 = 0. (2.3.5)
Solution of equation (2.3.5) yields the flat galactic curves. Various approaches are possible. One approach is, for any particular galaxy, to determine ρb from luminosity measurements, then solve equations (2.2.1) and (2.3.5) simultaneously, for Vc and ρ as functions of R.
Another approach is described in the Appendix. The results are as follows:
1) Vc reaches a limit at sufficiently large R:
Vc,lim = (4πGk)1/4 (2.3.6)
2) For large dense galaxies, Vc asymptotically reaches the limit from higher values according to:
 . (2.3.7)
. (2.3.7)
3) For small galaxies, Vc asymptotically rises to the limit from lower values according to:
(Vc)4 = (Vc,lim)4 – constant/R2 (2.3.8)
2.4. A Tully-Fisher Relation
In keeping with the simplicity of spherical symmetry, we consider a hypothetical galaxy of large luminous (baryonic) mass but small radius, and the region outside its small luminous radius.
Substituting into equation (2.5) for ρr2 from equation (2.2.1) and for 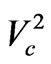 from equation (2.3.12), and then integrating, yields:
from equation (2.3.12), and then integrating, yields:
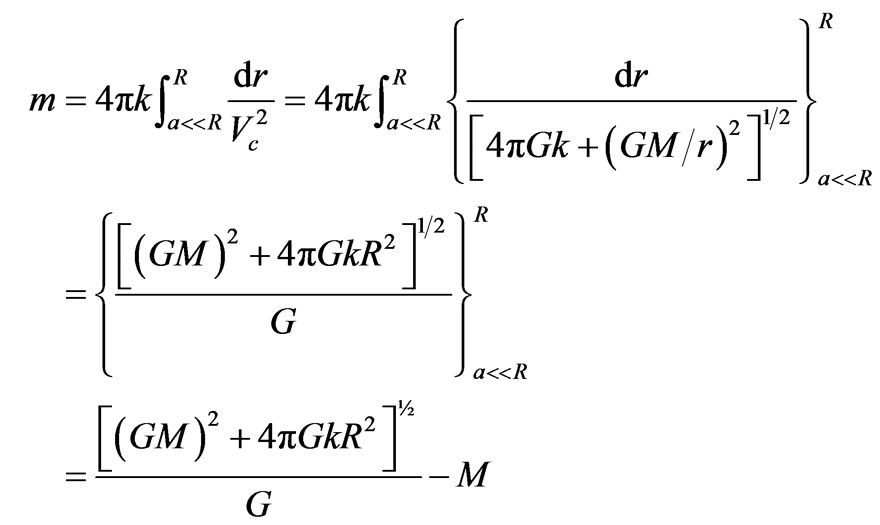 .(2.4.1)
.(2.4.1)
2.4.1. At Sufficiently Large Distance from Mass Center: Galactic Flat Rotation Curve
For sufficiently large distances Rlarge from the center of M, equation (2.4.1) yields:
 . (2.4.1.1)
. (2.4.1.1)
Equations (2.4.1 and 2.4.1.1) show that for  , the DM mass m increases linearly with Rlarge, consistent with galactic flat rotation curves.
, the DM mass m increases linearly with Rlarge, consistent with galactic flat rotation curves.
2.4.2. At Sufficiently Small Distances from Mass Center
For sufficiently small distances Rsmall from the center of M, equation (2.4.1) yields:
 (2.4.2.1)
(2.4.2.1)
Equation (2.4.2.1) shows that for:
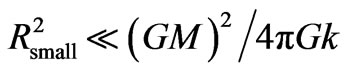 , (2.4.2.2)
, (2.4.2.2)
the DM-mass m around M increases in proportion to (Rsmall)2, contributing an added constant accelerationterm:
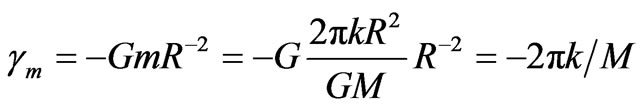 , (2.4.2.3)
, (2.4.2.3)
that is, directed towards the center of M.
Equation (2.4.2.3) is valid around a star like the Sun and would explain very nicely all the observations about the Pioneer Anomaly except for the Viking ranging data [29-31].
2.4.3. Tully-Fisher Relation
Expressing k from equation (2.4.2.3) as:
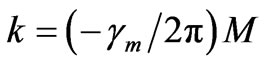 (2.4.3.1)
(2.4.3.1)
and then substituting into equation (2.1.13) yields:
 (2.4.3.2)
(2.4.3.2)
The above results apply outside any galaxy, where DM is spherically symmetric1,3,4,10 and Dm = 0. In particular, they apply outside spiral galaxies so that equation (2.4.3.2) expresses a TFR. However, just like Milgrom’s MOND relation, equation (2.4.3.2) expresses a relation of the baryonic mass M with the limit velocity Vc,limit, while the TFR is with the maximum (peak) circular velocity Vc,max.
2.5. Derivation of Milgrom’s Relation
Milgrom’s MOND relation may be derived from the properties of DM, without departing from Newton laws by substituting for k from equation (2.4.3.1) into equation (2.3.8):
Vc,lim = −(2GγmM)1/4 > 0 for sufficiently small acceleration. (2.5.1)
Equation (2.5.1) is the MOND correlation (1.1.8) at sufficiently small acceleration. Comparison with equation (1.1.8) yields:
γo = −2γm > 0 (2.5.2)
Substituting for −2γm from Equation (2.5.1):
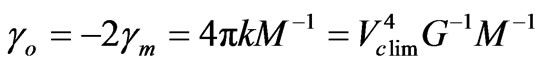 (2.5.3)
(2.5.3)
According to equation (2.5.3), γo is not strictly identical for all galaxies but should exhibit some variation over different galaxies, because even galaxies of equal mass have slightly different k-values for different distributions of their masses.
Assuming the Sun gravitates around our Galaxy center at about the limiting speed, equation (2.5.3) yields for our Galaxy:
γo = (2.2 × 107 cm·s−1)4 (6.67 × 10−8 cm3·s−2·g−1)−1
[(6 × 1010)(1.989 × 1033 g)]−1 = 2.9 × 10−8 cm·s−2, (2.5.4)
which is of the order of magnitude of the value prescribed by Milgrom, thus contributing some credibility to our treatment.
According to this derivation, Milgrom’s relation applies to equilibrium or quasi-equilibrium conditions, and therefore is not applicable to collision of galaxy clusters.
Therefore, all the results obtained with MOND derive also from the elastically compressible model of DM. This result is important because MOND’s relation has been shown to fit very well galactic rotation curves and the Tully-Fisher relation [32-34].
2.6. Elastic Compressibility of Dark Matter
The elastic compressibility of DM plays a crucial role in establishing a DM pressure, a DM EoS, and perhaps an understanding of DM behavior. It behooves us to derive an expression for that elastic compressibility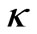 :
:
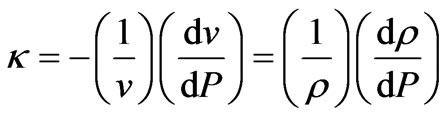 , (2.6.1)
, (2.6.1)
where v is the volume of a fixed mass m of DM at pressure P.
Forming the derivatives on both sides of equation (2.1.4) and substituting for 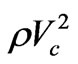 from equation (2.2.1):
from equation (2.2.1):
 (2.6.2)
(2.6.2)
Differentiating equation (2.2.1):
 (2.6.3)
(2.6.3)
Substituting from equations (2.6.2 and 2.6.3) into equation (2.6.1) yields:
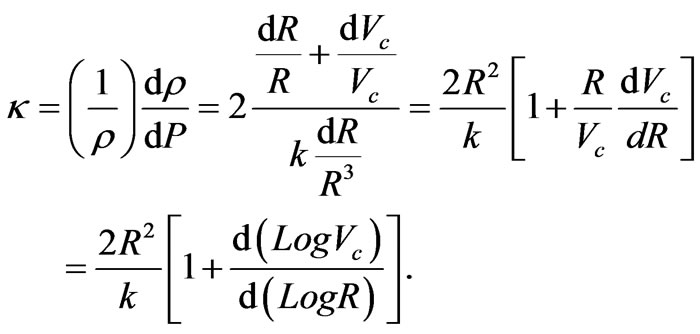 (2.6.4)
(2.6.4)
When R becomes sufficiently large, then
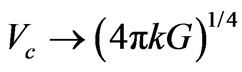 and
and 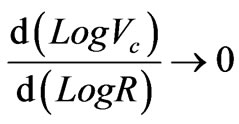 yielding:
yielding:
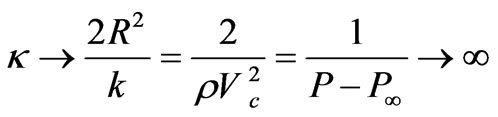 . (2.6.5)
. (2.6.5)
When R becomes sufficiently small, then Vc also becomes very small and  so that
so that
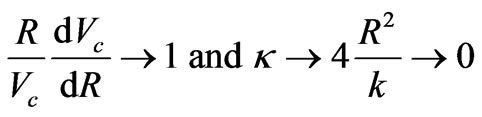 (2.6.6)
(2.6.6)
2.7. Accelerated Expansion of Our Universe
In a Universe where all mass is embodied in particles, after the Big Bang, gravitation tends to slow down the initial expansion of our Universe. In such a Universe, even DM contributes to the gravitation forces and, therefore, to slowing down the expansion of the Universe of particles.
For simplicity, consider two galaxies, their center-tocenter line, and the distance between the two galaxies expanding due to an initial big bang impetus. The gravitation attraction between the two galaxies tends to slow down that expansion. Intergalactic DM adds to the galaxies mass and therefore to the gravitation thus contributing to further slowing down the expansion.
However, in our Universe an elastically compressible DM can produce a different result: with the two galaxies pulling the DM in opposite directions, somewhere along that line, there is a point X where the pulls of the two galaxies balance each other. The DM on each side of X is pulled away from X thus expanding it even though its pressure tends to zero. The infinite compressibility/decompressibility (equation (2.6.5)) facilitates that expansion. This contribution to the expansion of the intergalactic DM is above, and in addition to, the contribution from the initial impetus. The decompression of DM between galaxies might contribute to the accelerated expansion of our Universe. Thus, the elastically compressible DM under pressure could be a DE candidate.
3. Discussion and Conclusions
3.1. Nature of Dark Matter
The non-particulate, massive, and elastically compressible DM model is an alternative “new physics” because it is not constituted of particles.
The hypotheses that DM is constituted of WIMPs or that DM is elastically compressible are in conflict with each other because the self-interactions of WIMPs are not strong enough to produce the elastic compressibility and pressure sufficient to balance the gravitational pull.
If DM is not constituted of particles, we are left with a fluid continuum, which makes it unlike any known other substance, and some of its properties must be unlike any property of known other substances.
From observations we know that it does not emit electromagnetic radiation, neither does it absorb nor reflect any: it is perfectly transparent. Its only known interaction with baryonic matter is gravitational. Similarly, with electromagnetic radiation that is deflected gravitationally in lensing.
At this time, we do not know if DM exhibits a refractive index. In the affirmative, we do not know if it does vary, and perhaps how it varies, with DM density ρ.
If it were not for its distributed mass density, DM could be identified with space, which raises the question: does space have a distributed mass density? That would make space a substance! Some might object that this would be a kind of revival of ether, which has been definitely disqualified more than a hundred years ago.
Others may hold that the ether was never proven wrong, only unnecessary, given the knowledge of the time, but is needed now. That the existence of measured physical properties of space: electrical permittivity, magnetic permeability, both in concordance with the speed of light, support the material nature of space.
If this model of DM is allowed to be published, it would be expected to become controversial: some will hold that the success of the consequences derived from the model do not prove its validity. In particular, anything not made of particles is unthinkable. Others may hold, as is generally accepted in science, that the success speaks in favor of the model, that the existence of a DM particle is not proven at all and that to reject a non-particulate DM because of the unsubstantiated belief in a DM particle is tantamount to dogmatism.
However, physicists and astrophysicists are entitled to a fair hearing of that model as much as to the concepts of DM WIMPs, or to other alternative “new physics.” Whether they compromise and accept to explore the model of non-particulate DM remains to be seen.
3.2. Tully-Fisher Relation
Like Milgrom’s MOND relation, the relation derived here is between the luminous mass of a galaxy and the limiting speed of the galactic rotation curve, while the Tully-Fisher relation is with the maximum (peak) speed. However, Milgrom tailored his relation, ad hoc, and in conflict with general relativity, while the derivation in this paper is based on the properties of DM without conflict with general relativity.
3.3. Relation between Baryonic and Dark Matter Distributions
Equations (2.2.1) and (2.3.1) provide the relation between the baryonic matter and the DM distributions, sometimes dubbed the halo-disc conspiracy (for spiral galaxies). This is the first known derivation of such relation, and can be tested against data from existing galactic rotation curves.
3.4. Derivation of Milgrom’s Relation
Because the Milgrom relation at weak acceleration fits very well galactic rotation curves and the Tully-Fisher relation, the derivation of those relations from the DM model supports that model. However, as already stated, according to our derivation, Milgrom’s relation applies only to equilibrium and quasi-equilibrium conditions and is not valid for collisions.
3.5. Power of the Model
The power of the model is demonstrated in part by its ability to derive:
1) An equation of state for DM.
2) A relation between DM and baryonic matter distributions.
3) Galactic flat rotation curves.
4) A Tully-Fisher relation.
5) Milgrom’s MOND relation.
6) A possible mechanism for black hole formation at the centers of large galaxies.
7) A possible mechanism for the acceleration of our Universe expansion.
4. Acknowledgements
I thank my colleague Dan Zuras of Hewlett-Packard, Palo Alto, California, for stimulating discussions and for very helpful suggestions in the early stage of this work; Virginia Trimble of the University of California at Irvine, California, for close reading of an earlier manuscript, for very helpful comments, and for unfailing encouragement. The support of all the librarians at Hewlett-Packard Laboratories and at Agilent Technologies is gratefully acknowledged.
REFERENCES
- J. Silk, “The Big Bang,” Freeman and Company, New York, 1989.
- M. S. Turner, “Dark Matter in the Universe,” Physica Scripta, Vol. 1991, No. T36, 1991, p. 167. doi:10.1088/0031-8949/1991/T36/018
- S. M. Faber and J. S. Gallagher, “Masses and Massto-Light Ratio of Galaxies,” Annual Review of Astronomy and Astrophysics, Vol. 17, pp. 135-187. doi:10.1146/annurev.aa.17.090179.001031
- V. C., Rubin, “The Rotation of Spiral Galaxies,” Science, Vol. 220, No. 4604, 1983, pp. 1339-1344. doi:10.1126/science.220.4604.1339
- V. C. Rubin, “Constraints on Dark Matter from Optical Rotation Curves,” Proceedings of the IAU Symposium, Princeton, 24-28 June1987, pp. 51-62.
- T. S. Albada and R. Sancisi, “Dark Matter in Spiral Galaxies [and Discussion],” Philosophical Transactions of the Royal Society, Vol. 320. No. 1556, 1986, pp. 447- 464.
- J. Binney and S. Tremaine, “Galactic Dynamics,” Princeton University Press, Princeton, 1987.
- J. Kormendy and J. R. Knapp, “Dark Matter in the Universe,” Reidel, Dordrercht, 1987.
- V. Trimble, “Existence and Nature of Dark Matter,” Annual Review of Astronomy and Astrophysics, Vol. 25, 1987, pp. 425-472. doi:10.1146/annurev.aa.25.090187.002233
- S. Tremaine “The Dynamical Evidence for Dark Matter,” Physics Today, 1902, February, 28.
- A. Burkert and J. Silk, “The Intriguing Distribution of Dark Matter in Galaxies,” The Astrophysical Journal Letters, Vol. 488, No. 2, 1997, p. 488. doi:10.1086/310935
- S. Cebrian, et al., “Search for Dark Matter with CRESST,” Astroparticle Physics, vol. 21, No. 1, 2004, pp. 23-34.
- T. Jageman, “CRESST Detector for Nonbaryonic Cold Dark Matter Particles,” International Astronomical Union Symposium No. 220, Sydney, 21-25 July 2004, Australia, p. 493.
- M. J. Lewis and K. Freese, “The Phase of the Annual Modulation as a Tool for Determining the WIMP Mass,” Physics Review, vol. 70, No. 4, 2004, pp. 043501-043508.
- G. Nollez, “Status of the EDELWEISS Dark Matter Search,” Semaine de l’Astrophysique Française, Paris, 14-18 June 2004.
- M. Milgrom, “A Modification of the Newtonian Dynamics as a Possible Alternative to the Hidden Mass Hypothesis,” The Astrophycical Journal, Vol. 270, 1983, pp. 365-370.
- M. Milgrom, “A Modification of the Newton DynamicsImplications for Galaxies,” The Astrophycical Journal, Vol. 270, 1983, p. 371.
- M. Milgrom, “A Modification of the Newton Dynamics —Implications for Galaxy Systems,” The Astrophycical Journal, Vol. 270, 1983, p. 384.
- M. Milgrom, “Isothermal Spheres in the Modified Dynamics,” The Astrophysical Journal, Vol. 287, 1984, pp. 571-576.
- M. Milgrom, “Solutions for the Modified Newtonian Dynamics Field Equation,” Astrophysical Journal, Vol. 302, 1986, pp. 617-625.
- M. Milgrom and J. Bekenstein, “Dwarf Galaxies of the Local Group—M. Mateo,” Astrophysical Journal, Vol. 286, 1984, p. 7.
- J. D. Bekenstein, “The Missing Light Puzzle: aHint About Gravity?” Proceeding of 2nd Canadian Conference on General Relativity and Relativistic Astrophysics, Toronto, 14-16 May 1987.
- R. H. Sanders, “Mass Discrepancies in Galaxies. Dark Matter and Alternatives,” Astronomy and Astrophysics Review, Vol. 2, No. 1, 1990, pp. 1-28. doi:10.1007/BF00873540
- S. Kent, “Dark Matter in Spiral Galaxies. II. Galaxies with H1 Rotation Curves,” Astrophysical Journal, Vol. 93, No. 4, 1987, pp. 816-832.
- A. Edery, “The Bright Side of Dark Matter,” 1999, Physical Letter Review, Vol. 83, No. 20, 1999, pp. 3990- 3992. doi:10.1103/PhysRevLett.83.3990
- V. C. Rubin, “Invited Talk at Foothill College,” Los Altos, 2002.
- D. Clowe, et al., “A Direct Empirical Proof of the Existence of Dark Matter,” The Astrophysical Journal Letters, Vol. 648, No. 2, 2006, p. L109. doi:10.1086/508162
- K. C. Freeman, “Parameters for Dark Halos,” In: J. Kormendy and G. R. Knapp, Eds., Dark Matter in the Universe, Reidel, Dordrercht, 1987, p. 119.
- J. D. Anderson, P. A. Laing, E. L. Lau, A. S. Liu, M. M. Nieto and S. Turyshev, “Indication, from Pioner 10/11, Galileo, and Ulysses Data, of an Apparent Anomalous, Weak, Long-Range Acceleration,” Physical Review Letters, Vol. 81, No. 14, 1998, pp. 2858-2861.
- J. D. Anderson, P. A. Laing, E. L. Lau, A. S. Liu, M. M. Nieto and S. Turyshev, “Study of the Anomalous Acceleration of Pioneer 10 and 11,” Physical Review Letters, Vol. 65, 2002, p. 082004.
- S. G. Turyshev, M. M. Nieto, J. D. Anderson, “Lessons Learned from the Pioneers 10/11 for a Mission to Test the Pioneer Anomaly,” Advances in Space Research, Vol. 39, 2004, pp. 291-296.
- W. J. G. De Blok and S. S. McGaugh, “Testing Modified Newton Dynamics with Low Surface Brightness Galaxies —Rotation Curve Fits,” The Astrophysical Journal, Vol. 508, No. 1, 1998, pp. 132-140. doi:10.1086/306390
- S. S. McGaugh, “The Mass Discrepancy-Acceleration Relation: Disk Mass and the Dark Matter Distribution,” The Astrophysical Journal, Vol. 609, No. 2, 2004, pp. 652- 666. doi:10.1086/421338
- S. S. McGaugh and W. J. G. De Blok ”Testing the Hypothesis of Modified Dynamicsa with Low Surface Brightness Galaxies and Other Evidence,” The Astrophysical Journal, Vol. 499, No. 1, 1998, pp. 66-81. doi:10.1086/305629
Appendix
In section 2.3 of the present paper, it was stated that solution of equation (2.3.5) yields the flat galactic rotation curves. One suggested approach is, for any particular galaxy, to determine the luminous mass density ρb from luminosity measurements, then solve equations (2.2.1) and (2.3.5) simultaneously, for the galactic rotation speed Vc and for the DM density ρ, as functions of R. Equations (2.2.1 and 2.3.5) are reproduced here as equations (A1 and A2, respectively) for the reader’s convenience:
−ρR3 = ρ(Vc)2R2 = k. (A1)
G4πk(ρb/ρdR/R + 4πGk[dR/R] − (Vc)4dR/R − (Vc)2d(Vc)2 = 0. (A2)
Another approach consists of the consideration of two simpler cases:
1) Equation (A2) is solved first for the case of large galaxies where the rotation speed rises fast with R, reaches speeds larger than the plateau, reaches a maximum speed, then beyond the luminous region, slows down and asymptotically reaches the plateau speed limit.
Beyond the luminous radius R0 (0 < R0 < R) of a galaxy, the luminous mass M becomes constant so that dM = 0 and equation (A2) becomes 4πGk[dR/R] = (Vc)4dR/R + (Vc)2d(Vc)2
or
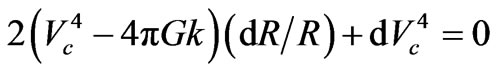 . (A3)
. (A3)
A singular solution of equation (A3) is:
Vc = (4πGk)1/4 (A4)
When , then from equation (A3):
, then from equation (A3):
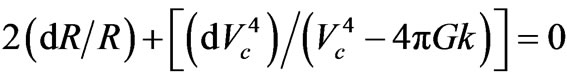 and, upon integration,
and, upon integration, 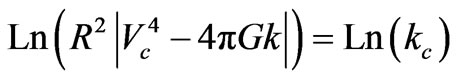 or:
or:
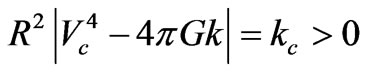 . (A5)
. (A5)
Equation (A5) yields:
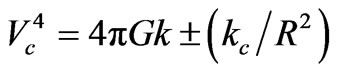 . (A6)
. (A6)
Equations (A5) and (A6) are valid outside the luminous radius of any galaxy, where dM = 0 and DM mass density is spherically symmetric.
Equation (A6) shows that, as Rlarge becomes sufficiently large, the speed Vc tends to a limit Vc,lim given by:
Vc,lim = (4πGk)1/4, (A7)
thus establishing the galactic flat rotation curve and the DM mass density distribution of equation (A1).
To determine the value of kc, first we consider the gravitation outside the luminous region, that is for R > R0 where M is constant, 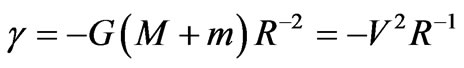 from which:
from which:
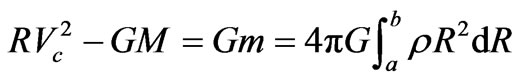 (A8)
(A8)
Second, we substitute under the integral for ρR2 from Equation (A1) and then for 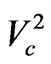 from equation (A6) to obtain:
from equation (A6) to obtain:
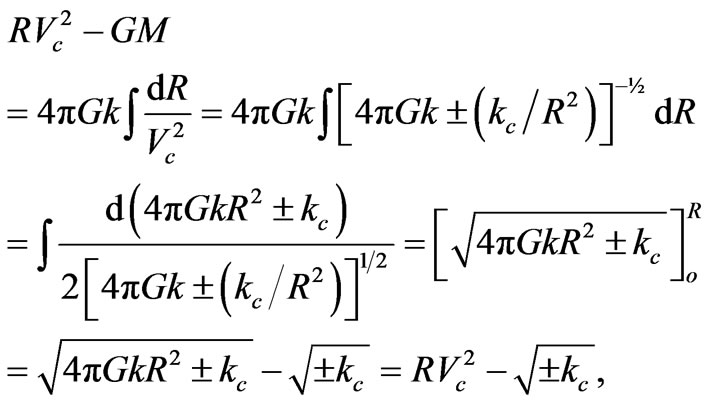
from which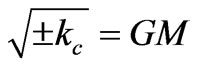 . Because kc > 0, the negative sign under the square root is unacceptable and equations (A5) and (A6) yield only one branch, for R > R0:
. Because kc > 0, the negative sign under the square root is unacceptable and equations (A5) and (A6) yield only one branch, for R > R0:
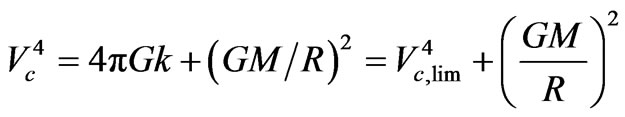 . (A9)
. (A9)
Equation (A9) shows the speed Vc asymptotically approaching the speed limit from higher speeds, as is the case for large dense galaxies where the circular speed initially rises fast, then slows down, reaches a maximum, and comes down to a plateau. It does not represent the cases of small dense galaxies that behave differently.
From equation (A1), along the rotation speed plateau:
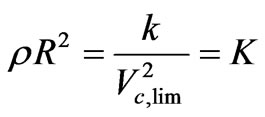 , another constant. (A10)
, another constant. (A10)
Comparing equation (A9) to equation (2.3.10) yields:
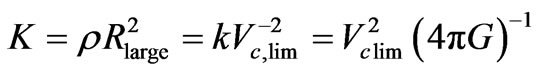 , (A11)
, (A11)
where the constant k is expressed from equation (A7) as:
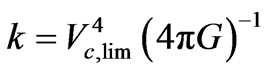 (A12)
(A12)
The above results are similar to those of Milgrom’s MOND.
We now derive the galactic flat plateau in cases of smaller galaxies where the rotation curve asymptotically rises to the plateau from lower speeds.
2) Within the luminous region, for R < R0, equation (A2) is valid, G4πkρb/ρdR/R + 4πGk[dR/R] − (Vc)4dR/R − (Vc)2d(Vc)2 = 0, and substituting (Vc,lim)4 for 4πGk, we obtain:
[(Vc,lim)4 – (Vc)]4](dR/R) = (Vc)2d(Vc)2]
– (Vc,lim)4(ρb/ρ) dR/R or:
2[(Vc,lim)4 (1 – ρb/ρ) – (Vc)]4](dR/R) = d(Vc)4 (A13)
As R becomes sufficiently large, the luminous matter mass density becomes negligible and equation (A13) becomes:
2[(Vc,lim)4 – (Vc)]4](dR/R) = d(Vc)4 (A14)
The solution of Equation (A14) is 2Log (R) + Log[(Vc,lim)4 – (Vc)4] = Log (constant) from which:
(Vc)4 = (Vc,lim)4 – constant/R2 (A15)
Equation (A15) shows (Vc)4 rising linearly with R–2 at a decreasing slope and asymptotically reaching the speed limit Vc,lim.

