Journal of Modern Physics
Vol. 2 No. 10 (2011) , Article ID: 8051 , 5 pages DOI:10.4236/jmp.2011.210140
Harmonic Oscillator with Fluctuating Mass
Department of Physics, Bar-Ilan University, Ramat-Gan, Israel
E-mail: gittem@mail.biu.ac.il
Received April 29, 2011; revised June 5, 2011; accepted June 20, 2011
Keywords: Stochastic Oscillator, Random Mass, Stability
ABSTRACT
We generalize the previously considered cases of a harmonic oscillator subject to a random force (Brownian motion), or having random frequency, or random damping. We consider here a random mass which corresponds to an oscillator where the particles of the surrounding medium adhere to the oscillator for some (random) time after collision, thereby changing the oscillator mass. Such a model is appropriate to chemical and biological solutions as well as to some nano-technological devices. The first moment and stability conditions for white and dichotomous noise are analyzed.
1. Introduction
Brownian motion is described by the dynamic equation of a harmonic oscillator supplemented by thermal noise 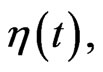
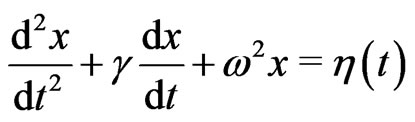 (1)
(1)
with the correlation function
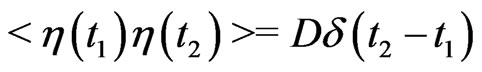 (2)
(2)
The random force 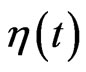 enters Equation (1) additively. When the noise has an external origin rather than an internal origin, the associated noise enters the equation of motion multiplicatively. If the noise arises from the fluctuations of the potential energy
enters Equation (1) additively. When the noise has an external origin rather than an internal origin, the associated noise enters the equation of motion multiplicatively. If the noise arises from the fluctuations of the potential energy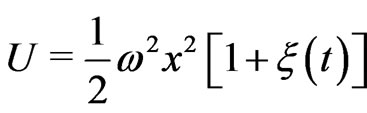 the equation of motion (1) takes the following form
the equation of motion (1) takes the following form
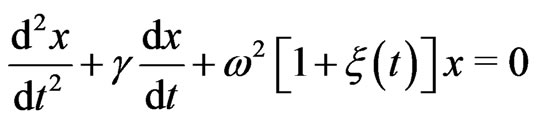 (3)
(3)
Another possibility for the generalization of the dynamic Equation (1) is the inclusion of random damping
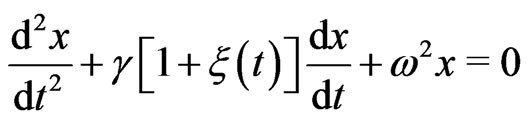 (4)
(4)
There are many applications in physics, chemistry and biology of the models described by equations (3) and (4) [1].
We recently studied [2] still another possibility for introducing randomness in the oscillator Equation (1), by considering an oscillator with a random mass, which describes a new type of Brownian motion-Brownian motion with adhesion. In this situation the molecules of the surrounding medium not only randomly collide with the Brownian particle, which produces its well-known zigzag motion, but they also stick to the Brownian particle for some (random) time, thereby changing its mass. The appropriate equation of motion has the following form
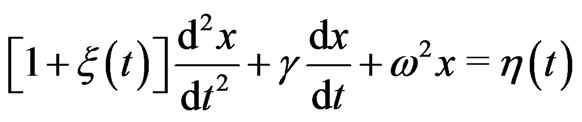 (5)
(5)
Among applications of (5) is an RLC electrical circuit subject to a voltage 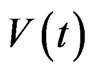 with a fluctuating inductance
with a fluctuating inductance 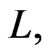 which is described by the following equation
which is described by the following equation
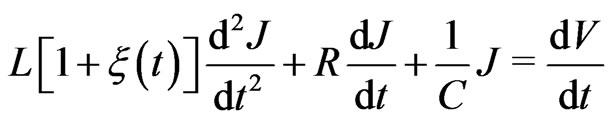 (6)
(6)
There are many situations in which chemical and biological solutions contain small particles which not only collide with a large particle, but they may also adhere to it. The diffusion of clusters with randomly growing masses has also been considered [3]. There are also some applications of a variable-mass oscillator [4]. Modern applications of such a model include a nanomechanical resonator which randomly absorbs and desorbs molecules [5]. The aim of this note is to describe a general and simplified form of the theory of an oscillator with a random mass, which is a useful model for describing different phenomena in Nature.
2. Model
We have to modify Equation (5) slightly since this equation describes the dynamic equation with a mass that can both increase or decrease due to fluctuations. As distinct from Equations (3) and (4), we replace 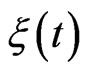 in Equation (5) by a positive random force
in Equation (5) by a positive random force 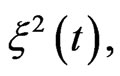 which corresponds to the fact that the mass of the Brownian particle can only increase due to the adhesion of the molecules of the surrounding medium,
which corresponds to the fact that the mass of the Brownian particle can only increase due to the adhesion of the molecules of the surrounding medium,
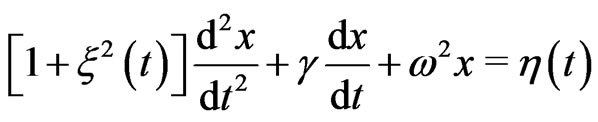 (7)
(7)
We consider the simple form of color noise—the asymmetric dichotomous noise (random telegraphic process), which means that the random variable 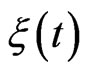 takes values
takes values 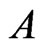 or
or 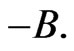 Denote the rate of transition for
Denote the rate of transition for 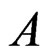 to
to 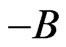 by
by![]() , and the reverse rate by
, and the reverse rate by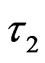 . For this form of the Ornstein-Uhlenbeck noise, the correlation function is
. For this form of the Ornstein-Uhlenbeck noise, the correlation function is
 (8)
(8)
For the limiting case of white noise, 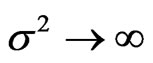 and
and 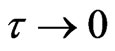 with
with 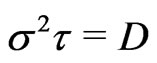 remaining constant,
remaining constant,
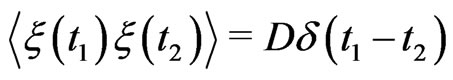 (9)
(9)
The quadratic noise 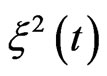 can be written as
can be written as
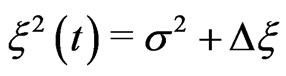 (10)
(10)
with 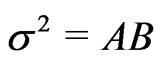 and
and 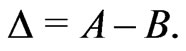 Indeed, for
Indeed, for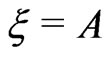 , one obtains
, one obtains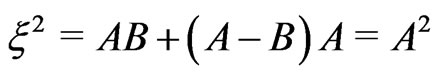 , and for
, and for 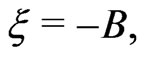
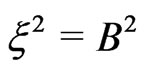
Equation (7) then takes the following form,
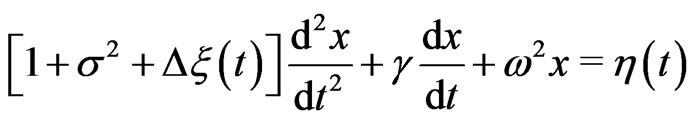 (11)
(11)
3. First Moment
First of all, one has to transfer the stochastic Equation (11) to the deterministic equations for the average values 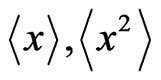 etc. For this purpose we use the well-known Shapiro-Loginov procedure [6] which yields for exponentially correlated noise (8)
etc. For this purpose we use the well-known Shapiro-Loginov procedure [6] which yields for exponentially correlated noise (8)
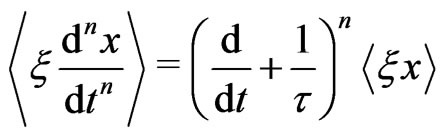 (12)
(12)
Inserting (12) into (11) (with ) one obtains, after averaging,
) one obtains, after averaging,
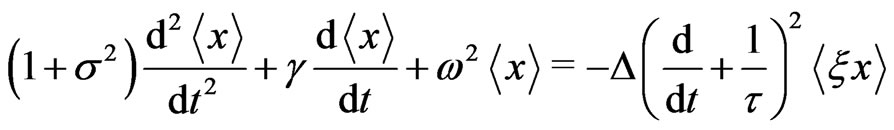 (13)
(13)
A new function 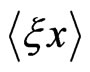 enters Equation (13). A second equation for the two functions
enters Equation (13). A second equation for the two functions 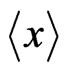 and
and 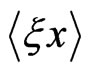 can be obtained by multiplying Equation (11) by
can be obtained by multiplying Equation (11) by 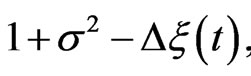
using Equation (12) and the following exact expression for the exponentially correlated noise, for splitting averages [7]
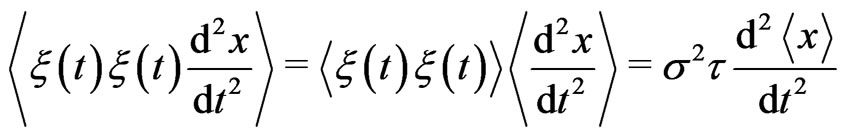 (14)
(14)
which gives
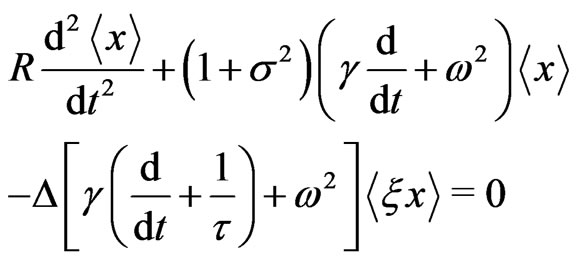 (15)
(15)
where 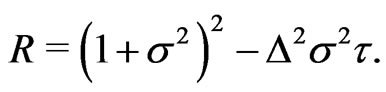 It was assumed that there is no correlation between the internal and external sources of noise,
It was assumed that there is no correlation between the internal and external sources of noise,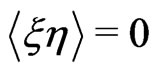 .
.
The advantage of dichotomous noise is that the averaging procedure (14) allows one to avoid an infinite system of high-order correlations. Excluding the correlator 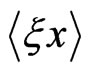 from Equations (13) and (15), one obtains a cumbersome fourth-order differential equation for
from Equations (13) and (15), one obtains a cumbersome fourth-order differential equation for ![]() which we do not write here. In a similar way one can find the equations for the second moment
which we do not write here. In a similar way one can find the equations for the second moment 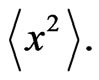
4. Stability Conditions
Here we consider the much less trivial problem of the stability of the solutions. For a deterministic equation, the stability of the fixed points is defined by the sign of![]() , found from the solution of the form
, found from the solution of the form 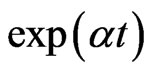 of a linearized equation near the fixed points. The situation is quite different for a stochastic equation. The first moment
of a linearized equation near the fixed points. The situation is quite different for a stochastic equation. The first moment 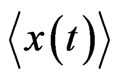 and higher moments become unstable for some values of the parameters. However, the usual linear stability analysis, which leads to instability thresholds, turns out to be different for different moments making them unsuitable for the stability analysis. A rigorous mathematical analysis of random dynamic systems shows [8] that, similar to the order-deterministic chaos transition in nonlinear deterministic equations, the stability of a stochastic differential equation is defined by the sign of Lyapunov exponents
and higher moments become unstable for some values of the parameters. However, the usual linear stability analysis, which leads to instability thresholds, turns out to be different for different moments making them unsuitable for the stability analysis. A rigorous mathematical analysis of random dynamic systems shows [8] that, similar to the order-deterministic chaos transition in nonlinear deterministic equations, the stability of a stochastic differential equation is defined by the sign of Lyapunov exponents![]() . This means that for stability analysis, one has to go from the Langevin-type Equations (3), (4) and (11) to the associated FokkerPlanck equations which describe properties of statistical ensembles.
. This means that for stability analysis, one has to go from the Langevin-type Equations (3), (4) and (11) to the associated FokkerPlanck equations which describe properties of statistical ensembles.
The Lyapunov exponent ![]() is defined as the exponential divergence rate of neighboring trajectories [8], i.e., as
is defined as the exponential divergence rate of neighboring trajectories [8], i.e., as
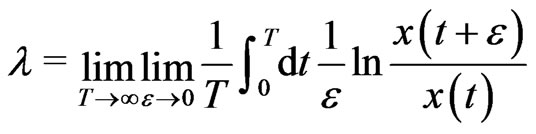 (16)
(16)
It is convenient to take limit 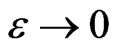 first. Then, after substituting in (16) the expansion
first. Then, after substituting in (16) the expansion 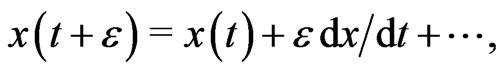 one obtains
one obtains
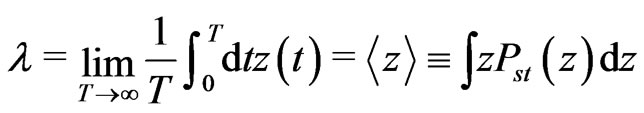 (17)
(17)
where the new variable 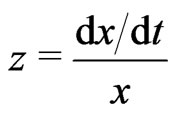 has been introducedand
has been introducedand 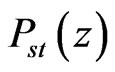 is the stationary solution of the FokkerPlanck equations corresponded to the Langevin equations expressed in the variable
is the stationary solution of the FokkerPlanck equations corresponded to the Langevin equations expressed in the variable![]() Turning from the variable
Turning from the variable ![]() in the Langevin Equations (5), (6) and (11) to the variable
in the Langevin Equations (5), (6) and (11) to the variable 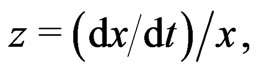 one gets
one gets
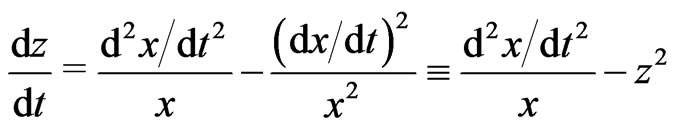 (18)
(18)
Multiplying Equation (11) with 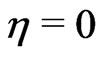 by
by 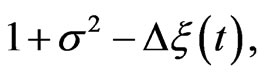 one obtains
one obtains
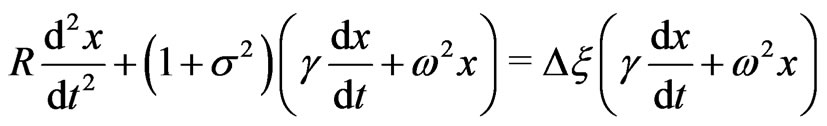 (19)
(19)
Replacing the variable ![]() by the variable
by the variable 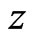 leads to
leads to
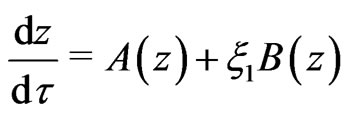 (20)
(20)
where
 (21)
(21)
4.1. White Noise
First, we start with white noise for which
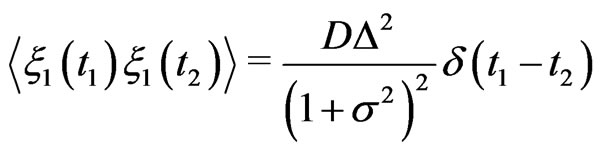 (22)
(22)
The Fokker-Planck equation associated with Equation (5) has the following form ( Stratonovich interpretation) [9]
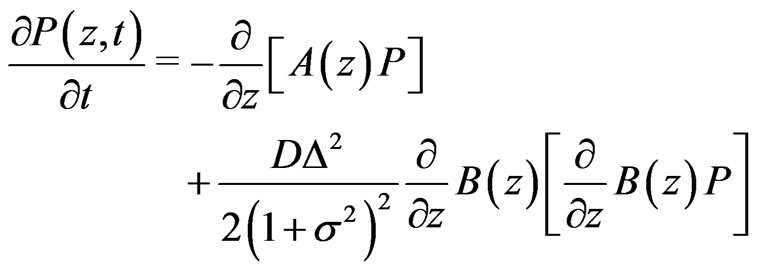 (23)
(23)
which, for the stationary case reduces to
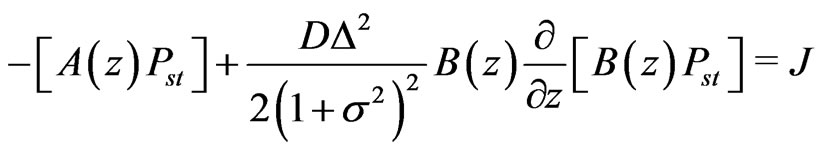 (24)
(24)
where ![]() is the constant probability current.
is the constant probability current.
The solution of the homogeneous Equation (24) (with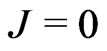 ) is
) is
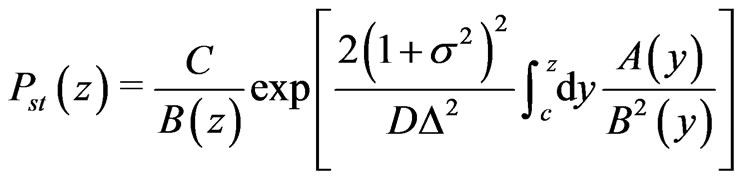 (25)
(25)
The solution of the inhomogeneous Equation (24) can be obtained by the method of variation of constants, which leads to
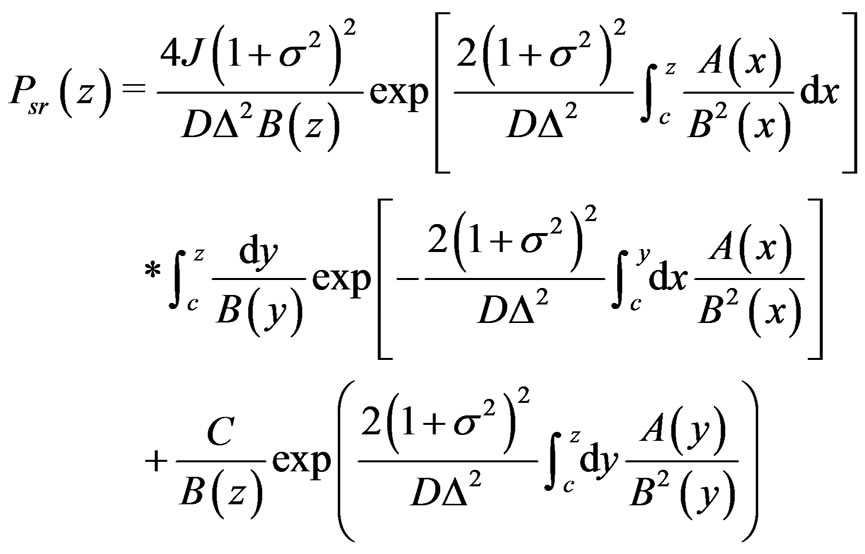 (26)
(26)
The constant 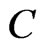 and the reference point
and the reference point ![]() are not important for our analysis, and we may assume
are not important for our analysis, and we may assume 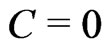 for
for ![]()
Inserting (21) into (26), one transforms Equation (26) to the following form,
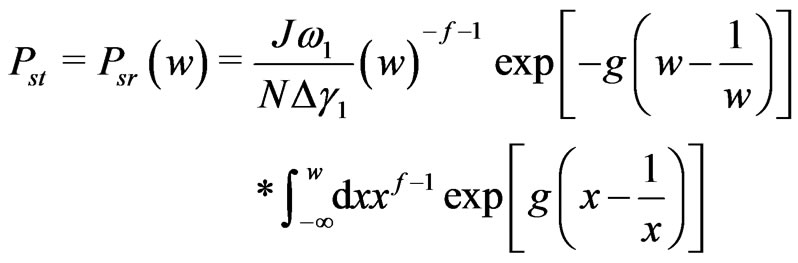 (27)
(27)
where
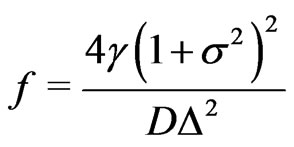 (28)
(28)
There is no need to perform an analysis of Equation (27), since the analogous calculation has been performed for the case of random damping [10] yielding the following result after substitution in Equation (17),
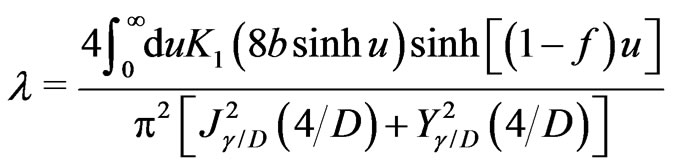 (29)
(29)
where 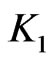 is a modified Bessel function of the second kind, and
is a modified Bessel function of the second kind, and ![]() and
and ![]() are Bessel functions of the first and second kind, respectively. The Bessel functions are always positive, and the sign of the Lyapunov exponent
are Bessel functions of the first and second kind, respectively. The Bessel functions are always positive, and the sign of the Lyapunov exponent ![]() is the same as the sign of the hyperbolic function
is the same as the sign of the hyperbolic function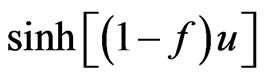 , i.e., the sign of
, i.e., the sign of 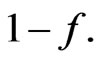
Therefore, an oscillator with fluctuating mass becomes unstable when 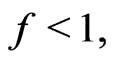 i.e., the instability of the fixed point
i.e., the instability of the fixed point 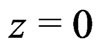 occurs for
occurs for 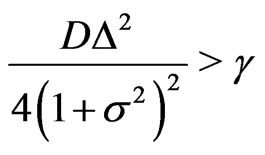 and does not depend on the oscillator frequency
and does not depend on the oscillator frequency![]() .
.
4.2. Dichotomous Noise
According to [11,12], the stationary solution of the Fokker-Planck equation, corresponding to the Langevin Equation (19) having the correlation function (8), has the following form
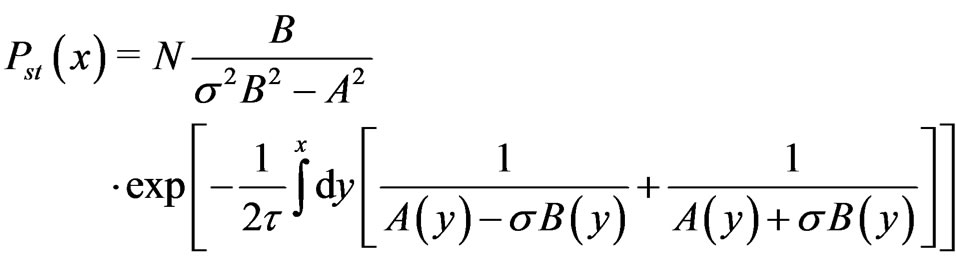 (30)
(30)
Equation (30) has been analyzed for different forms of functions 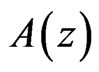 and
and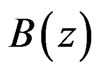 :
:
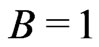
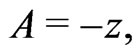 [13];
[13]; 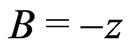
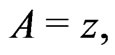 [14] ;
[14] ;
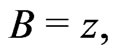
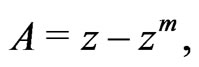 [15];
[15];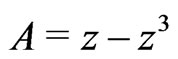 ,
, 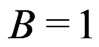 [16];
[16];
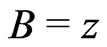
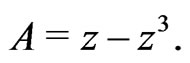 [17,18];
[17,18]; 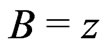
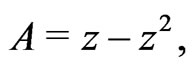 [11,12].
[11,12].
The zeroes of functions 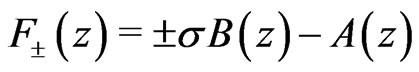 determine the boundary of
determine the boundary of 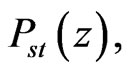 which diverges or vanishes at the boundaries and determine the boundary of support of
which diverges or vanishes at the boundaries and determine the boundary of support of 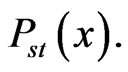 The latter means that a system will approach the state
The latter means that a system will approach the state 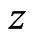 located in intervals
located in intervals 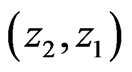 or
or 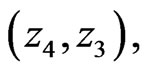 depending on its initial position. Another important characteristic of
depending on its initial position. Another important characteristic of 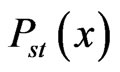 is location of its extrema, which define the macroscopic steady states. The steady states
is location of its extrema, which define the macroscopic steady states. The steady states 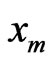 of (30) obey the following equation [11,12].
of (30) obey the following equation [11,12].
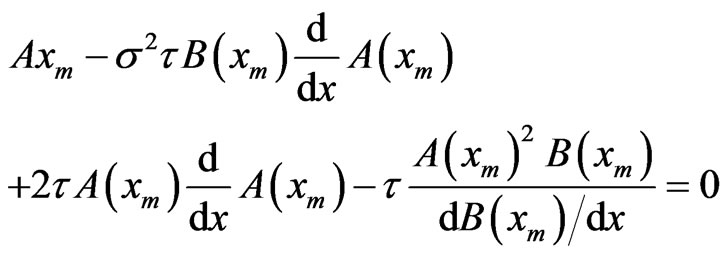 (31)
(31)
The first term in (31) defines the deterministic steady states while the first two terms relate to the white noise limit (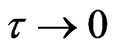
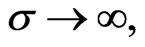 with
with 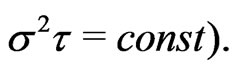 Finally, the last two terms define the corrections coming from the final correlation time
Finally, the last two terms define the corrections coming from the final correlation time 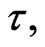
For
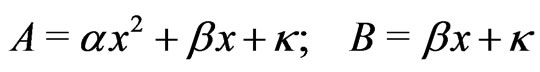 (32)
(32)
with, according to (21),
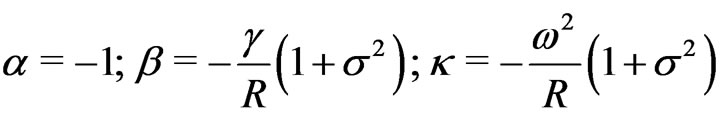 (33)
(33)
one obtains
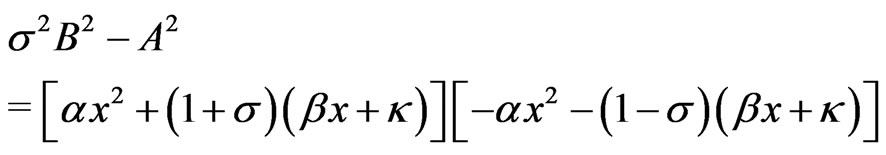 (34)
(34)
and
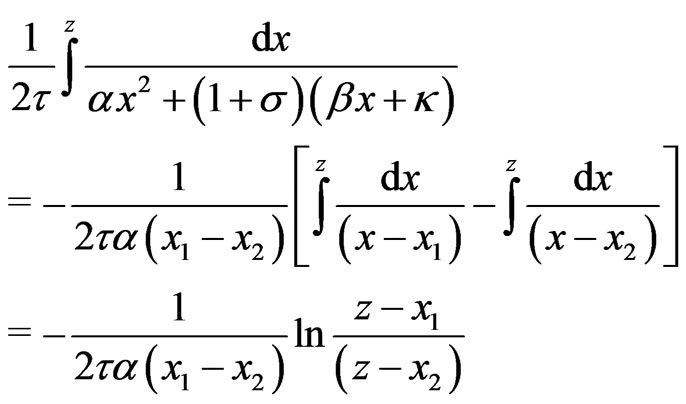 (35)
(35)
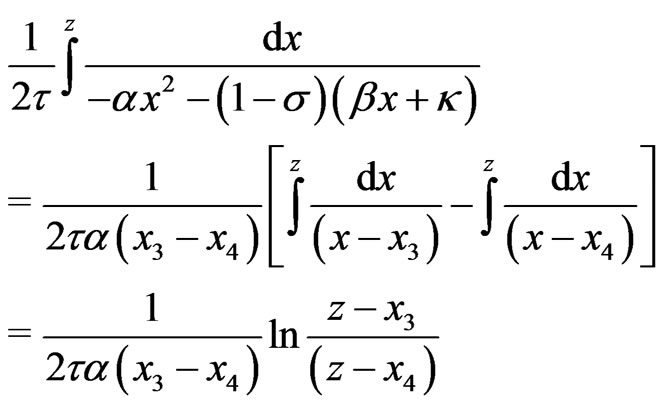 (36)
(36)
where
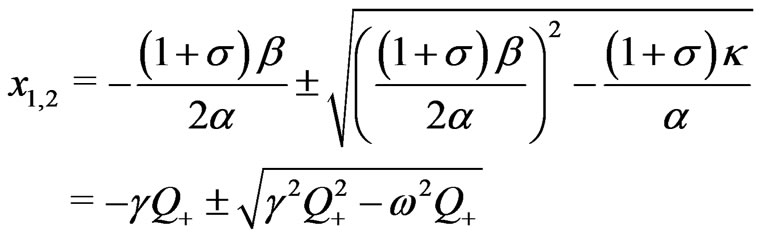 (37)
(37)
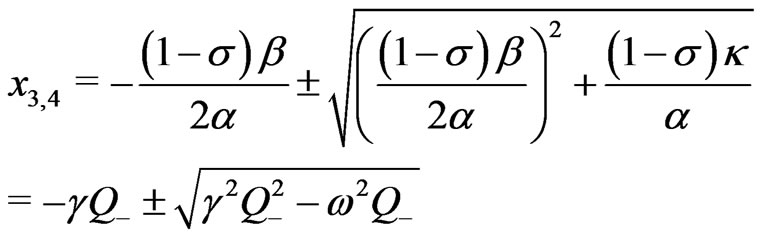 (38)
(38)
with
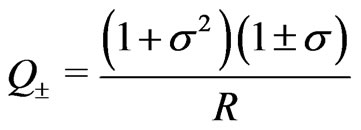 (39)
(39)
Inserting (32)-(38) into (30) gives
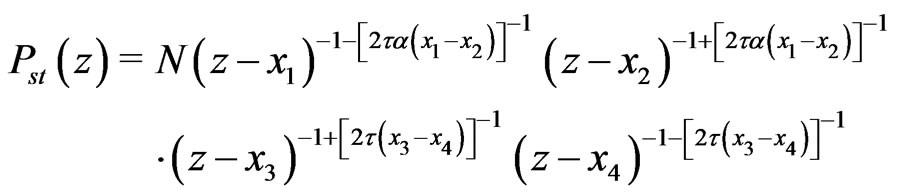 (40)
(40)
which, according to (17), defines the boundary of stability of the fixed point 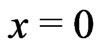 for different values of parameters
for different values of parameters 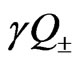 and
and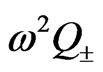 , which depend on characteristics
, which depend on characteristics 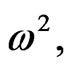
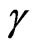 of an oscillator and
of an oscillator and 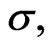
![]() and
and ![]() of noise.
of noise.
5. Conclusions
We have introduced a new model of a stochastic oscillator having a fluctuating mass, which, among other processes, describes Brownian motion with adhesion. That is, the particles of the surrounding medium not only collide with the Brownian particle but also adhere to it for some (random) time after the collision, thereby changing its mass. For white and dichotomous sources of noise, one can find the two first moments. A detailed stability analysis has been performed for white and dichotomous noise.
REFERENCES
- M. Gitterman, “The Noisy Oscillator: the First Hundred Years, from Einstein until Now,” World Scientific, Singapore, 2005.
- M. Gitterman, “New Stochastic Equation for a Harmonic Oscillator: Brownian Motion with Adhesion,” Journal of Physics C, Vol. 280, 2010, p. 012049
- J. Luczka, P. Hanggi and A. Gadomski, “Diffusion of Clusters with Randomly Growing Masses,” Physical Review E, Vol. 51, No. 6, 1995, pp. 5762-5769.
- M. S. Abdalla, “Time-Dependent Harmonic Oscillator with Variable Mass under the Action of a Driving Force,” Physical Review A, Vol. 34, No. 6, 1986, pp. 4598-4605. doi:10.1103/PhysRevA.34.4598
- J. Portman, M. Khasin, S. W. Shaw and M. I. Dykman, “The Spectrum of an Oscillator with Fluctuating Mass and Nanomechanical Mass Sensing,” Bulletin of the American Physical Society, March Meeting 2010, Vol. 55, No. 2, Portland, 15-19 March 2010, Abstract V14.00010.
- V. E. Shapiro and V. M. Loginov, “Formula of Differentiation and Their Use for Solving Stochastic Equation,” Physica A, Vol. 91, No. 3-4, 1978, pp. 563-574. doi:10.1016/0378-4371(78)90198-X
- R. C. Bourret, U. Frish and A. Pouquet, “Brownian Motion of Harmonic Oscillator with Stochastic Frequency,” Physica A, Vol. 65, No. 2, 1973, pp. 303-320.
- L. Arnold, “Random Dynamic Systems,” Springer, Berlin, 1998.
- N. G. van Kampen, “Stochastic Processes in Physics and Chemistry,” Elsevier, North-Holland, 1992.
- N. Leprovost, S. Aumaitre and K. Mallick, “Stability of a Nonlinear Oscillator with Random Damping,” European Physical Journal, Vol. 49, 2006, pp. 453-458.
- K. Kitahara, W. Horsthemke and R. Lefever, “ColoredNoise Induced Transitions: Exact Results for External Dichotomous Markovian Noise,” Physics Letters A, Vol. 70, 1979, pp. 377-380.
- K. Kitahara, W. Horsthemke and R. Lefever, “Phase Diagrams of Noise Induced Transitions,” Progress Theoretical Physics, Vol. 64, 1980, pp. 1233-1247. doi:10.1143/PTP.64.1233
- V. I. Klyatskin, “Dynamic Systems with Parameter Fluctuations of the Telegraphic Process Types,” Radiophysics and Quantum Electronics, Vol. 20, 1977, pp. 384-393. doi:10.1007/BF01033925
- V. Berdichevsky and M. Gitterman, “Stochastic Resonance in Linear Systems Subject to Multiplicative and Additive Noise,” Physical Review E, Vol. 60, No. 2, 1999, pp. 1494-1499.
- F. Sasagawa, “Critical Slowing Dawn in Random Growing-Rate Models with General Two Level Markovian Noise,” Progress Theoretical Physics, Vol. 69, No. 3, 1983, pp. 790-800. doi:10.1143/PTP.69.790
- K. Ouchi, T. Horita and H. Fujisaka, “Critical Dynamics of Phase Transition Driven by Dichotomous Markov Noise,” Physical Review E, Vol. 74, 2006, p. 031106. doi:10.1103/PhysRevE.74.031106
- Y. Jia, X.-P. Zheng, X.-M. Hu and J.-R. Li, “Effect of Colored Noise in Stochastic Resonance in a Bistable System Subject to Multiplicative and Additive Noise,” Physical Review E, Vol. 63, 2001, p. 031107. doi:10.1103/PhysRevE.63.031107
- S. Z. Ke, D. J. Wu and L. Cao, “Phase Transitions in a Bistable System Driven by Two Colored Noise,” European Physical Journal B, Vol. 12, 1999, pp. 119-122. doi:10.1007/s100510050985

