Journal of Modern Physics
Vol. 2 No. 8 (2011) , Article ID: 7086 , 5 pages DOI:10.4236/jmp.2011.28095
First Principle Study of Cubic SrMO3 Perovskites (M = Ti, Zr, Mo, Rh, Ru)
1Department of Physics, Govt. Dungar College, Bikaner, India
2International College for Girls, Mansarovar, Jaipur, India
E-mail: avinashdaga2009@gmail.com
Received April 20, 2011; revised May 26, 2011; accepted June 15, 2011
Keywords: Ab-Initio Method, Perovskite, LDA Approximation, ABINIT
ABSTRACT
Lattice parameter and corresponding total free energy have been computed for cubic SrMO3 perovskites (M = Ti, Zr, Mo, Rh, Ru) using the first principle approach within Density functional theory. The results have been calculated using local density approximation (LDA) method. It is found that the calculated lattice parameter for all transition metal oxides are in good agreement with the available experimental data. The total free energy corresponding to this lattice constant has been calculated along with different components of the total free energy. All these calculations have been carried out using ABINIT computer code.
1. Introduction
Transition metal oxides (TMO) have been for a long time the subject of intense experimental and theoretical study. Especially d-band TMO are of interest because of their catalytic properties. They form a large, rich and still not well understood class of compounds. Among the several structures of types exhibited by ABO3 oxides the perovskite structure is probably the most well known and widely investigated. Perovskites SrMO3 attracts much attention from physicists and material scientists because of the unusual combination of their magnetic, electronic and transport properties [1,2].
Strontium titanate, SrTiO3, is a generic representative of transition metal oxides [3] which have perovskite crystalline structure. It is a cubic perovskite at room temperature with a tetragonal phase transition at 105 K. Another insulating perovskite is the strontium zirconate, SrZrO3 [4], with 4d-electrons, which is of interest because of its high temperature electronic properties. It can be used in high-voltage capacitor applications because of its high breakdown strengths as well as high dielectric constant. In addition to this, both SrTiO3 and SrZrO3 are suitable for use in high-temperature applications such as fuel cells, steam electrolysis and hydrogen gas sensors.
Unlike SrTiO3, SrZrO3 shows first orthorhombic (Pnma) to orthorhombic (Cmcm) at 970 K, then to tetragonal (I4/mcm) at 1100 K, and then to cubic (Pm3m) at 1400 K. This compound has a rather high melting temperature of about 2920 K; consequently it is cubic in a wide range of temperature where most of its useful applications take place.
Until recently, 4d transition metal oxides (TMO) have attracted less attention because they had the reputation of containing high density of impurities and crystalline defects and having more extended d-orbitals compared to 3d TMO they are believed to have insignificant electronelectron correlation. Yet, numerous studies have shown that this is no longer the case for some promising TMO such as ruthenates and molybdates. These oxides are observed to exhibit unconventional superconductivity [5] and research is going on to understand the mechanism [6] of this new quantum order due to strong electron-electron interaction. In addition to this, non-Fermi liquid behavior has been observed in SrRuO3 [7]. Pseudo gap formation [8], metal-insulator transitions [9,10] and high-voltage applications are the other significant properties which draw a considerable attention to 4d TMO.
In the present study we deal with the bulk electronic properties of SrMO3-type perovskites where M stands for Ti, Zr, Mo, Rh and Ru respectively. We have chosen perovskite crystals of a very simple, cubic Pm3m symmetry, in order to keep all computational conditions simple and identical.
The density functional theory (DFT) is an extremely successful approach for the description of ground state properties of metals, semiconductors, and insulators. The computer implementations of DFT have been found to be a highly productive tool for studying complex solid state systems. Among these, the plane wave pseudopotential technique which is based on the total energy of the system has become popular as the method of choice for computational solid state physics. The success of this technique is that it has allowed us to better understand materials and processes. It has deepened the interpretation of experimental findings. It has offered new possibilities to design novel materials and devices by giving precise quantitative physical predictions.
In order to perform first-principles DFT calculations we used the ABINIT computer code. This code is open source ab initio electronic structure calculation software and has been under continuous development.
The total energy of an atomic structure can be of interest when one is looking for specific equilibrium configurations and when minima of the total energy with respect to atomic positions and/or the shape and size of the unit cell is needed. In this work we have made firstprinciples pseudopotential calculations of lattice parameter and total energy along with its decomposition into various components for transition-metal oxides SrMO3 (M = Ti, Zr, Mo, Rh & Ru ) by means of the Local density approximation (LDA) within the density functional theory.
2. Calculation Method
The simplest and easiest way to implement density functional approximation is a local one, in which the functional is a simple integral over a function of the density at each point in space.
In this approximation,  is a sum of contributions from each point in space depending only upon the density at each point independent of other points and given by
is a sum of contributions from each point in space depending only upon the density at each point independent of other points and given by
 (1)
(1)
where  is the exchange-correlation energy per electron. The above relation is called as the local density approximation (LDA). In the present study we have used pseudopotential method based on density functional theory in the local density approximation (LDA).
is the exchange-correlation energy per electron. The above relation is called as the local density approximation (LDA). In the present study we have used pseudopotential method based on density functional theory in the local density approximation (LDA).
Study of the electronic and structural properties of a solid involves evaluation of the total energy of the system. It is essential for every ab initio calculation, because most of the physical properties depend on the total energies or on the differences between these energies. As an example, lattice parameter of a crystal is the parameter that minimizes the total energy.
The ABINIT code, which is based on the DFT using plane waves and pseudopotentials, has been utilized for the total energy and lattice parameter computation. Plane waves are used as a basis set for the electronic wave functions. In order to solve the Kohn-Sham equations, conjugate gradients minimization method is employed as implemented by the ABINIT code. The exchangecorrelation effects are taken into account within the Perdew-Wang scheme as parameterized by Ceperly and Alder. Self consistent calculations generate the DFT ground state, with associated energy and density. Broyden algorithm (with sudden stop of atoms) allowed finding the equilibrium configuration of the nuclei, for which the forces vanish.
ABINIT program admits many different types of pseudopotentials e.g. Troullier-Martins type, Goedecker type, Hartwigsen-type etc. which can be used suitably. We have used Hartwigsen-Goedecker-Hutter pseudopotential included in the ABINIT package for our calculations. Hartwigsen, Goedecker, and Hutter presented a generalized form of pseudopotential, in separable form by construction, which was numerically fitted for elements up to Rn.
The considered SrMO3 perovskites are assumed to have ideal cubic structure (e.g. Pm3m) where atomic positions in the elementary cell are M: 1a (0, 0, 0); O: 3d (0, 0, 1/2); and Sr: 1b (1/2, 1/2, 1/2). The electronic configurations are taken Ar3d24s2 for Ti, Kr4d25s2 for Zr, Kr4d54s1 for Mo, Kr4d75s2 for Rh, Kr4d65s2 for Ru, Kr5s2 for Sr and He2s22p4 for O. Here, the noble gas cores are distinguished from the sub-shells of valence electrons.
All of the calculations involve 5-atom cubic unit cell arranged in a perovskite structure. A dozen of input variables are needed to run the ABINIT code for the calculations. The main input variables have been listed in Table 1. First of all space group number of the perovskite is mentioned in the input file by “spgroup” parameter. Then the definition of the unit cell is included in the input file by “acell” parameter which gives the length scales by which dimensionless primitive translations are to be multiplied and is specified in Bohr atomic units. In order to define the atom types we include input variables “ntypat” and “znucl”, where “ntypat” gives the number of types of atoms and “znucl” gives nuclear charge Z of the elements.
To define various atoms we use variables “natom”

Figure 1. Cubic perovskite single unit cell.
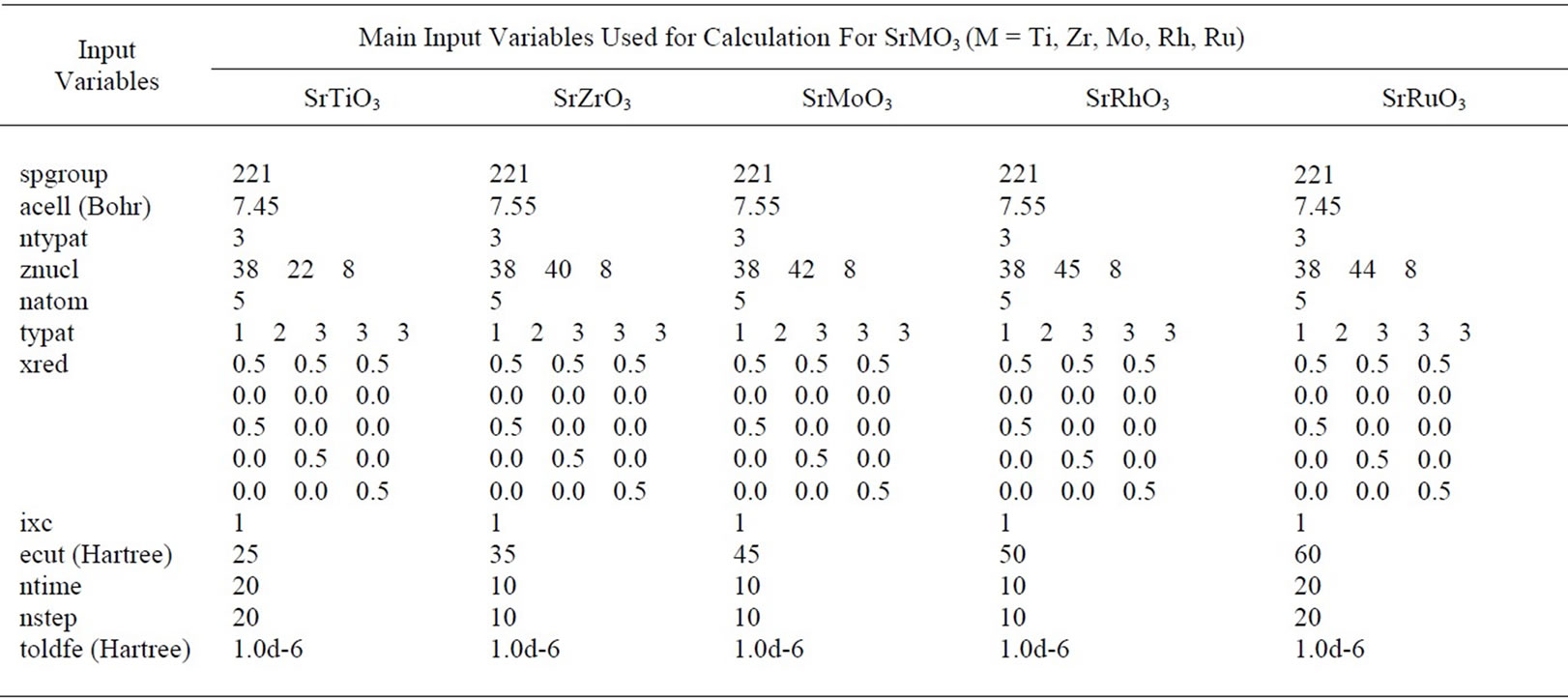
Table 1. Main input variables of SrMO3.
which gives the total number of atoms in the unit cell; “typat” which is an array that gives an integer label to every atom in the unit cell to denote its type; “xred” which gives the atomic locations within unit cell in coordinates relative to real space primitive translations. The array “typat” must agree with “xred” and “natom”.
In order to include exchange correlation functional we use “ixc” which is integer for LDA, Teter Pade parameterization. The plane wave basis set can be defined by “ecut” which is used for kinetic energy cutoff which controls number of plane waves at given k-points.
We get a good convergence for the bulk total energy calculation with the choice of cut-off energies at 25 Ha for SrTiO3, at 35 Ha for SrZrO3, at 45 Ha for SrMoO3, at 50 Ha for SrRhO3 and at 60 Ha for SrRuO3 using 4 × 4 × 4 Monkhorst-Pack mesh grid.
We then define the number of self-consistent field cycles (SCF) by variables “nstep” which gives the maximum number of SCF iterations and “toldfe” which sets a tolerance for absolute differences of total energy that reached twice successively, will cause one SCF cycle to stop. Apart from these variables input files also include variables for optimization of the lattice parameters and variables defining k-points grids.
3. Results and Discussions
In order to predict the lattice constant a series of total energy calculations are needed. Energy versus lattice constant curve is obtained from these calculations. Then the theoretical lattice parameter is the one which corresponds to the minimum of energy.
The lattice constants of the selected perovskites SrMO3, where M = Ti, Zr, Mo, Rh & Ru were calculated under constrain of cubic symmetry. Energy versus lattice constant curve for all the SMO3 perovskites under study are shown in the Figures 2-6.
The corresponding “acell” parameter for which minima of energy occurs is the lattice parameter for each perovskite. The results and some available experimental and theoretical data are summarized in Table 2.
The calculated lattice parameter for SrTiO3 is within 0.1% of the experimental results. It is also observed that calculated lattice parameter for SrZrO3 is within 0.8%; for SrMoO3 it is within 0.6% and for SrRhO3 it is within 0.3% of the experimental results. It is however seen that calculated lattice parameter for SrRuO3 is exactly in accordance with the available experimental results. Thus the calculated values are in accordance with the experimental results.
The difference in calculated and experimental values of the lattice parameter for all the perovskites under con-
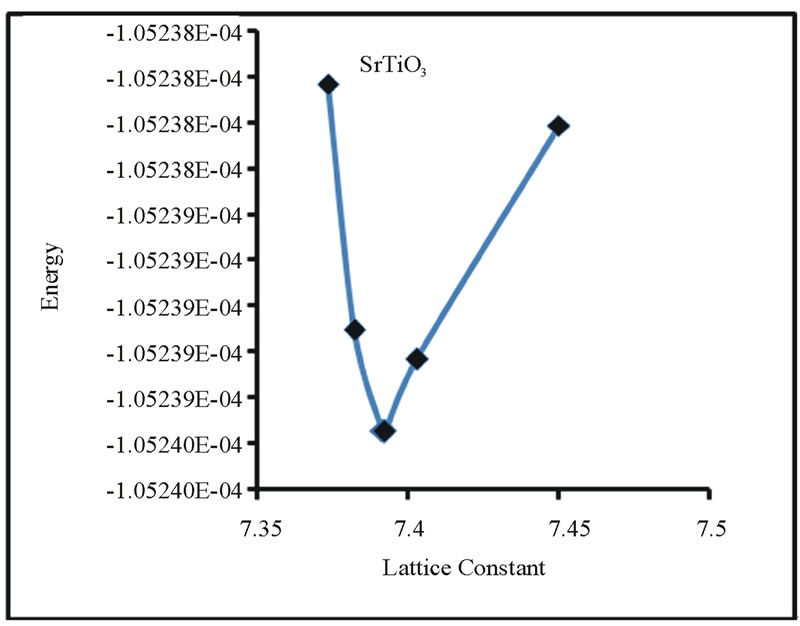
Figure 2. Total Energy versus acell for SrTiO3.
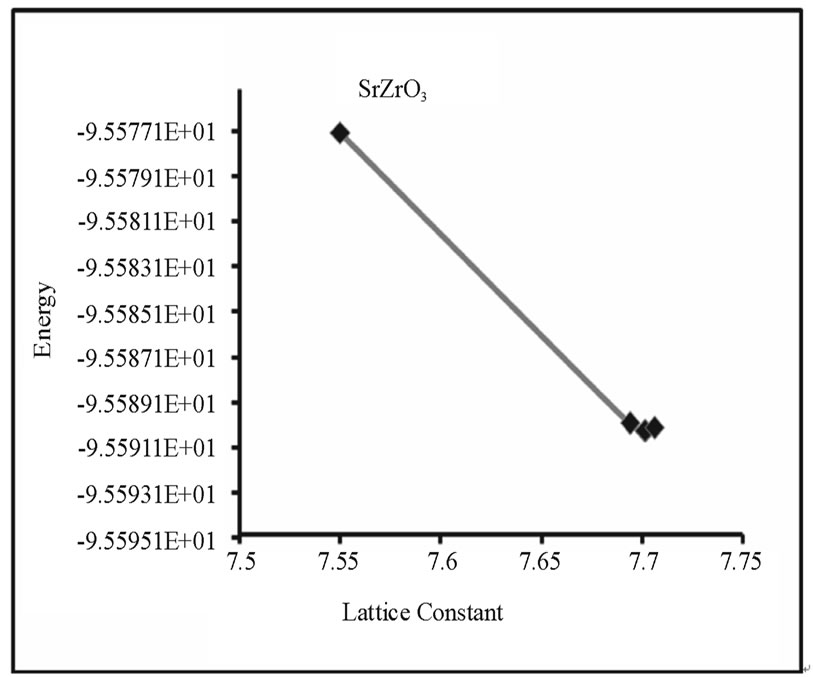
Figure 3. Total Energy versus acell for SrZrO3.
Figure 4. Total Energy versus acell for SrMoO3.
Figure 5. Total Energy versus acell for SrRuO3.

Figure 6. Total Energy versus acell for SrRhO3.
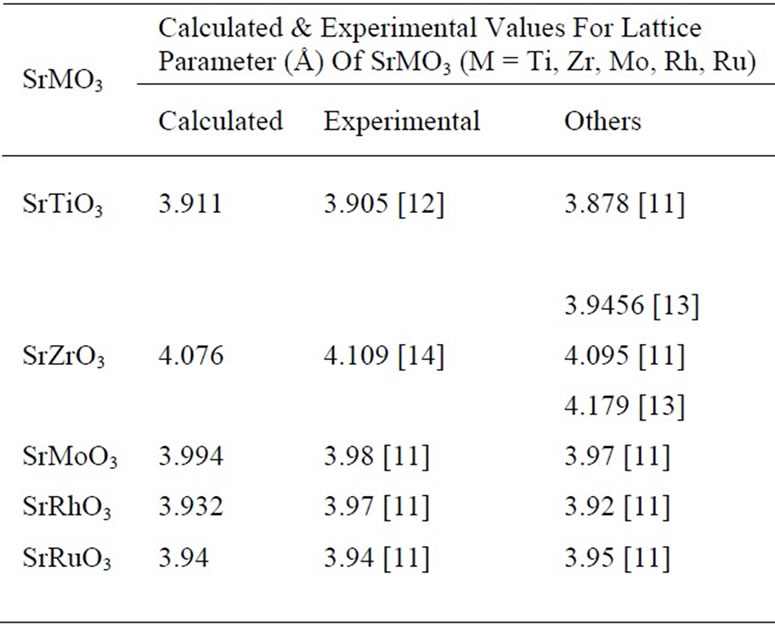
Table 2. Lattice parameter data of SrMO3.
siderations is not more than 0.8% which show the relevance of this approach.
In the case of SrTiO3, SrRhO3 & SrRuO3 comparisons of our results with the theoretical work of Mete et al. [11] and with the calculated values of Shein et al. [13] suggest that our pseudopotentials are as reliable and perform slightly better. Since the calculated lattice parameters are in good agreement with the experimental results, the corresponding total energy may be assumed to be correct The computed values of total free energy and the different components of the total energy for the all perovskites have been assembled in Table 3. The different components of total energy are kinetic energy, Hartree energy, exchange and correlation(XC) energy, Local pseudopotential energy, non-local pseudopotential energy, local pseudopotential “core correction” (PspCore) energy and Ewald energy.
4. Conclusions
The structural and electronic properties of five transition metal oxides, SrZrO3, SrTiO3, SrMoO3, SrRhO3, and SrRuO3 respectively with cubic perovskite structure are studied using an ab-initio pseudopotential method using ABINIT code.
Lattice parameters are found to compare well with the available data in the literature for all the perovskites showing the relevance of this approach. This approach can be further used in calculation of charge densities and band structures of these perovskites. A detailed description of their total free energy and its different components are given.
5. Acknowledgements
The authors (Avinash Daga and Smita Sharma) are grateful to the Principal, Dungar College Bikaner for pro-
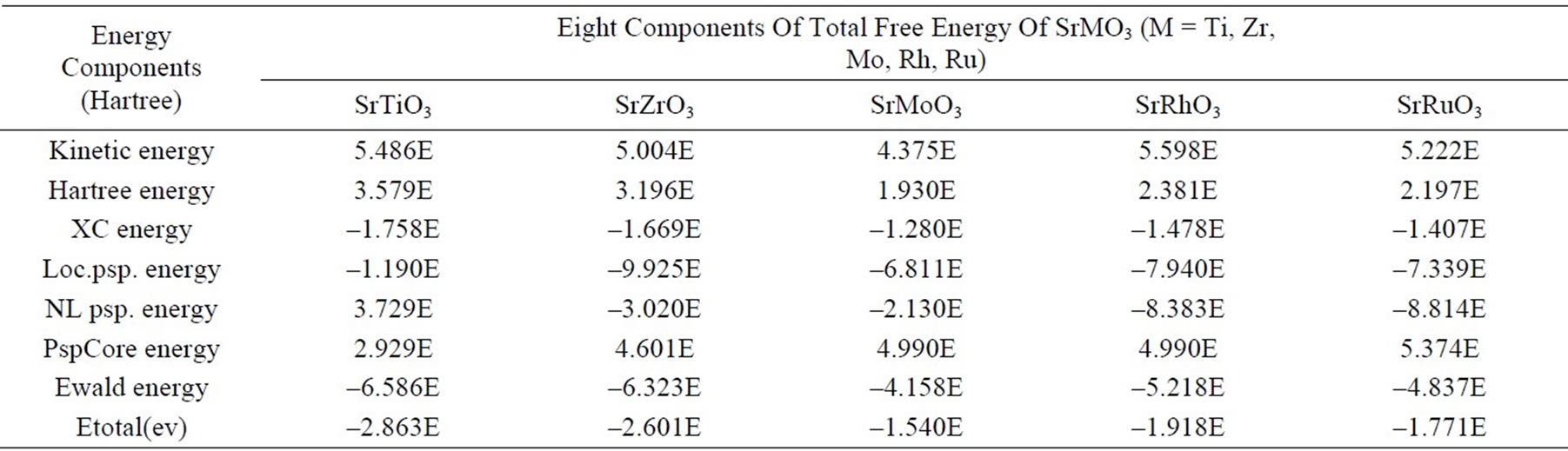
Table 3. Components of total free energy of SrMO3.
viding necessary facilities for this work. K.S. Sharma is grateful to the Director, International College for Girls (Autonomous) for the similar facilities provided for this work.
REFERENCES
- S. Takeno, T. Ohara, K. Sano and T. Kawakubo, “Novel Compositional Accommodation Mechanism in SrNbO3 by Analytical Electron Microscopy,” Surface Interface Analysis, Vol. 35, No. 1, 2003, pp. 29-35. doi:10.1002/sia.1488
- A. L. Shaula, V. V. Kharton, N. P. Vyshatko, E. V. Tsipis, M. V. Patrakeev, F. M. B. Marques and J. R. Frade, “Oxygen ionic transport in SrFe1−yAlyO3−δ and Sr1−xCaxFe0.5Al0.5O3−δ ceramics,” Journal of the European Ceramic Society, Vol. 25, No. 4, 2005, pp. 489-499. doi:10.1016/j.jeurceramsoc.2004.03.011
- B. K. Moon and H. Ishiwara, “Formation and Electrical Properties of Heteroepitaxial SrTiO3/SrVO3−x/Si(100) Structures,” Applied Physics Letters, Vol. 67, No. 14, 1995, pp. 1996-1998. doi:10.1063/1.114765
- M. Yoshino, K. Nakatsuka, H. Yukawa and M. Morinaga, “Local Electronic Structures around Hydrogen and Acceptor Ions in Perovskite-Type Oxide, SrZrO3,” Solid State Ionics, Vol. 127, No. 1-2, 2000, pp. 109-123. doi:10.1016/S0167-2738(99)00274-X
- Y. Maeno, H. Hashimoto, K. Yoshida, S. Nishizaki, T. Fujita, J. G. Bednorz and F. Lichtenberg, “Superconductivity in a Layered Perovskite without Copper,” Nature Vol. 372, 1994, pp. 532-534. doi:10.1038/372532a0
- T. Takimoto, T. Hotta, T. Maehira and K. Ueda, “Spin- fluctuation-induced superconductivity controlled by orbital fluctuation,” Journal of Physics: Condensed Matter, Vol. 14, No. 21, 2002, pp. L369-375. doi:10.1088/0953-8984/14/21/101
- P. Kostic, Y. Okada, N. C. Collins, Z. Schlesinger, J. W. Reiner, L. Klein, A. Kpitulnik, T. H. Geballe and M. R. Beasley, “Non-Fermi-Liquid Behavior of SrRuO3: Evidence from,” Physical Review Letters, Vol. 81, No. 12, 1998, pp. 2498-2501. doi:10.1103/PhysRevLett.81.2498
- Y. S. Lee, J. S. Lee, K. W. Kim, T. W. Noh, J. J. Yu, Y. K. Bang, M. K. Lee and C. B. Eom, “Pseudogap Formation in Four-Layer BaRuO3 and Its Electrodynamic Response Changes,” Physical Review B, Vol. 64, No. 16, 2001, Article ID: 165109. doi:10.1103/PhysRevB.64.165109
- J. S. Lee, Y. S. Lee, K. W. Kim, T. W. Noh, K. Char, J. Park, S. J. Oh, J. H. Park, C. B. Eom, T. Takeda and R. Kanno, “Optical Investigation of the Electronic Structures of Y2Ru2O7, CaRuO3, SrRuO3, and Bi2Ru2O7,” Physical Review B, Vol. 64, No. 24, 2001, Article ID: 245107. doi:10.1103/PhysRevB.64.245107
- T. Katsufuji, H. Y. Hwang and S. W. Cheong, “Anomalous magneto transport properties of R2Mo2O7 near the magnetic phase boundary,” Physical Review Letters, Vol. 84, No. 9, 2000, pp. 1998-2001. doi:10.1103/PhysRevLett.84.1998
- E. Mete, R. Shaltaf, and Ş. Ellialtıoğlu, “Electronic and Structural Properties of a 4d perovskite: Cubic phase of SrZrO3,” Physical Review B, Vol. 63, No. 3, 2003, Article ID 0304703.
- T. Mitsui and S. Nomura, “Numerical Data and Functional Relations in Science and Technology-Crystal and Solid State Physics,” Springer-Verlag, Berlin, 1982.
- I. R. Shein, V. L. Kozhevnikov and A. L. Ivanovskii, “First-Principles Calculations of the Elastic and Electronic Properties of the Cubic Perovskites SrMO3 (M = Ti, V, Zr and Nb) in Comparison with SrSnO3,” Solid State Sciences, Vol. 10, No. 2, 2008, pp. 217-225. doi:10.1016/j.solidstatesciences.2007.09.013
- A. J. Smith and A. J. E. Welch, “Some Mixed Metal Oxides of Perovskite Structure,” Acta Crystallographica, Vol. 13, 1960, pp. 653-656. doi:10.1107/S0365110X60001540

