Journal of Modern Physics
Vol. 2 No. 7 (2011) , Article ID: 5786 , 5 pages DOI:10.4236/jmp.2011.27079
Maximally Entangled States in the Hydrogen Molecule: The Role of Spin and Correlation
1Department of Physics, Sharif University of Technology, Tehran, Iran
2School of Physics, Institute for Studies in Theoretical Physics and Mathematics, Tehran, Iran
E-mail: vesaghi@sharif.edu
Received February 8, 2011; revised April 15, 2011; accepted April 28, 2011
Keywords: Hubbard Model, Entanglement, Hydrogen Molecule
ABSTRACT
Many electron calculations on a simplest realistic two electron system i.e. molecule was applied and as the consequence correlation effects was reflected accurately in the wavefunctions of H2. Zanardi’s entanglement measurement, demonstrated that the maximum of entanglement for the ground state happens when U = J and this resolved the controversial conclusion of U = 0 for maximum entanglement. It was shown that the ground and third excited states are maximally entangled. These maximally entangled states and also the minimally entangled states are correlated to their spin’s property. The wavefunctions of the not magnetic (S = 0) ground and excited states explicitly depend on correlation parameters whereas the first excited states which is magnetic (S2 = 2 and Sz
molecule was applied and as the consequence correlation effects was reflected accurately in the wavefunctions of H2. Zanardi’s entanglement measurement, demonstrated that the maximum of entanglement for the ground state happens when U = J and this resolved the controversial conclusion of U = 0 for maximum entanglement. It was shown that the ground and third excited states are maximally entangled. These maximally entangled states and also the minimally entangled states are correlated to their spin’s property. The wavefunctions of the not magnetic (S = 0) ground and excited states explicitly depend on correlation parameters whereas the first excited states which is magnetic (S2 = 2 and Sz 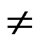 QUOTE
QUOTE 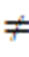
![]() 0) is not entangled. The second excited state is not magnetic but its wavefunction does not depend on correlation parameters therefore it is a moderately entangled state. In any case, by switching on a magnetic field an entangled state with Sz = 0 can be extracted from a not entangled degenerate magnetic state. We suggest that in a realistic molecular scale system, there is two criteria for finding maximally entangled electronic states, first the system should be in moderately correlated regime and second the system should have a non-magnetic (Sz = 0) electronic state.
0) is not entangled. The second excited state is not magnetic but its wavefunction does not depend on correlation parameters therefore it is a moderately entangled state. In any case, by switching on a magnetic field an entangled state with Sz = 0 can be extracted from a not entangled degenerate magnetic state. We suggest that in a realistic molecular scale system, there is two criteria for finding maximally entangled electronic states, first the system should be in moderately correlated regime and second the system should have a non-magnetic (Sz = 0) electronic state.
1. Introduction
Since Einstein, Podolsky and Rosen [1] and Schrödinger [2] investigated the non-classical properties of quantum systems and entered new concept as entanglement in to quantum physics, it had become strange property in interaction between particles. Recent study of the entanglement and achievement in this respect has become a useful resource for quantum communications and information processing [3] such as quantum teleportation [4,5], super dense coding [6], quantum key distribution [7], and quantum cryptography [8]. Entanglement also has been suggested as a quantitative measure for electron-electron (e-e) correlation in many body systems [9,10]. As a simple illustration of entanglement one can say that, if there is no way to write the states of two particles as a product of the states of two sub systems in the Hilbert space, then there will be an entangled system [11]. A lot of investigation has been done about measuring entanglement, such as the Wooters’ measure [12] and the Schliemann’s measure [13,14]. Through Gittings’ investigation [15], it is shown that all these entanglement measures are not suitable but the Zanardi’s measure [16,17] satisfies all desirable properties of entanglement measurement for fermionic systems.
H2 molecule is the simplest two electron systems that can be used to implement a many body calculation based on Hubbard model [18]. Traditional Hubbard model which is a priory many-body approach usually is used as a first attempt to calculate entanglement. This model gives maximum entanglement by setting e-e interaction parameter U = 0, which is a controversial conclusion [17,19,20]. To overcome this controversial conclusion a new calculation i.e. going beyond Hubbard model for obtaining entanglement of the non-magnetic ground and magnetic excited states of H2 molecule was done. The H2 molecule is one of the simplest realistic two electrons correlated systems in nature which our model can be implemented with considering all direct and exchange interaction terms beyond Hubbard model. This implementation lets us consider correlation effects more accurately in the wavefunctions. Zanardi’s measurement was employed for calculating entanglement. To find the effect of the spin on the entanglement of states; the ground and excited state of  was investigated and surprisingly the results give maximally entangled states with non-zero U value. We also discuss the difference between maximally, moderately and zero entangled states based on their spin and correlation.
was investigated and surprisingly the results give maximally entangled states with non-zero U value. We also discuss the difference between maximally, moderately and zero entangled states based on their spin and correlation.
2. Calculation Method
The complete Hubbard Hamiltonian is defined as [21]:
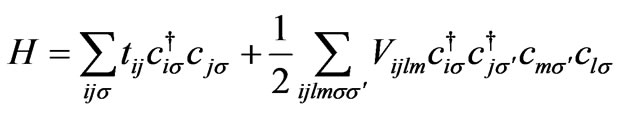 (1)
(1)
where  is hopping and on-site for electrons under the influence of both hydrogen nuclei and
is hopping and on-site for electrons under the influence of both hydrogen nuclei and 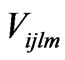 is all electron-electron interactions. The first term contains noninteracting part of Hamiltonian which can be written as:
is all electron-electron interactions. The first term contains noninteracting part of Hamiltonian which can be written as:
 (2)
(2)
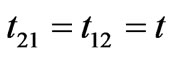 (3)
(3)
where 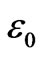 is the energy of atomic orbital,
is the energy of atomic orbital, 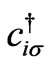 and
and 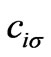 are fermionic creation and annihilation operators respectively on site i with spin s, and t stands for the hopping integral between two H atomic sites of the electrons with the same. The second term of Hamiltonian that contains e-e interaction part can be written as:
are fermionic creation and annihilation operators respectively on site i with spin s, and t stands for the hopping integral between two H atomic sites of the electrons with the same. The second term of Hamiltonian that contains e-e interaction part can be written as:
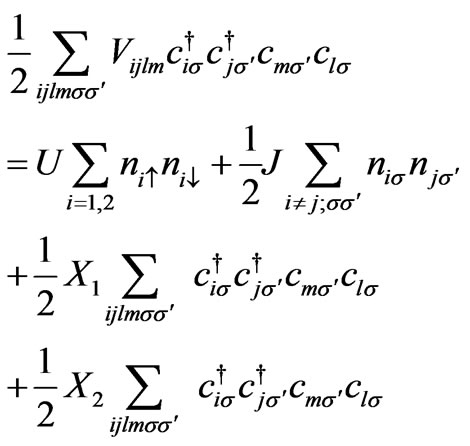 (4)
(4)
where Vijlm stands for all 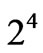 Coulomb interaction parameters between electrons, which is U as on-site Coulomb repulsion or V1111 and V2222, J as inter-site Coulomb repulsion or V1212 and V2121 and
Coulomb interaction parameters between electrons, which is U as on-site Coulomb repulsion or V1111 and V2222, J as inter-site Coulomb repulsion or V1212 and V2121 and 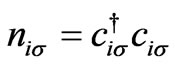 is density operator. The last terms X1 and X2 are the exchange interactions parameters that can only be interpreted by quantum mechanics and are demonstrated as:
is density operator. The last terms X1 and X2 are the exchange interactions parameters that can only be interpreted by quantum mechanics and are demonstrated as:

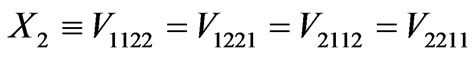 (5)
(5)
We consider two electrons of 1s orbital of two H atoms of H2 molecule with both spin orientations up and down, therefore we have four states for a single electron and as the result for their combination there are C(4,2)=6 states which are represented with notation 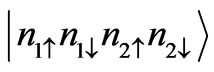 as :
as :
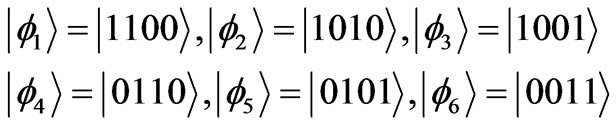 (6)
(6)
With these sets of states, the Hamiltonian parameters were calculated and Hamiltonian matrix is:
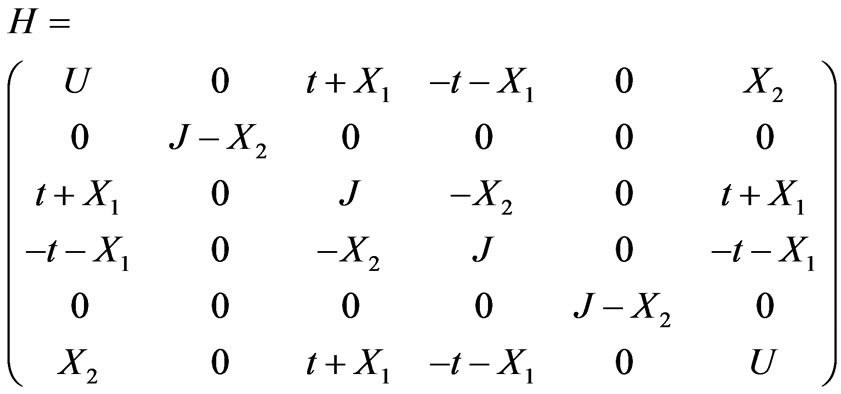 (7)
(7)
All the diagonal elements contain a term tii, where it is twice 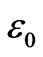 and this one is roughly two times of the energy of an electron in the 1s state of atomic hydrogen i.e.
and this one is roughly two times of the energy of an electron in the 1s state of atomic hydrogen i.e.  and are not written here. Using ab initio energies for H2 and the values of
and are not written here. Using ab initio energies for H2 and the values of 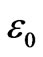 and t from [22] the Hamiltonian parameters, U, J, X1 and X2, were evaluated and are given in Table 1.
and t from [22] the Hamiltonian parameters, U, J, X1 and X2, were evaluated and are given in Table 1.
Entanglement measurement is defined by von Neumann’s entropy as [16]:
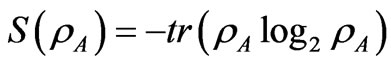 (8)
(8)
where A is the label of one of the subsystems which in our model is 1s orbital of one of the Hydrogen atoms and  is reduced density matrix defined as:
is reduced density matrix defined as:
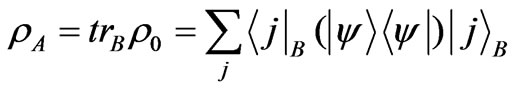 (9)
(9)
where 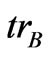 stands for tracing over all sites except the B sites and
stands for tracing over all sites except the B sites and  is eigenstates for B subsystem
is eigenstates for B subsystem  i.e.
i.e. 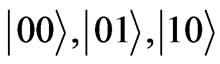 and
and . After this calculation, the reduced density matrix for the ground state (not normalized) becomes:
. After this calculation, the reduced density matrix for the ground state (not normalized) becomes:
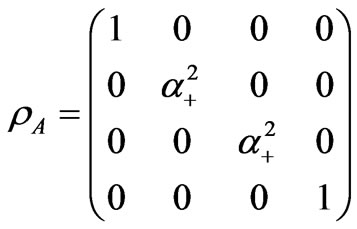 (10)
(10)
For other states, reduced density matrices have been evaluated accordingly and their entanglements were calculated. The resultant entanglement values are listed in Table 2. By action of S2 operator on the  eigenstates, one could find total spin of each state in
eigenstates, one could find total spin of each state in

Table 1. The calculated values of Hamiltonian parameters.
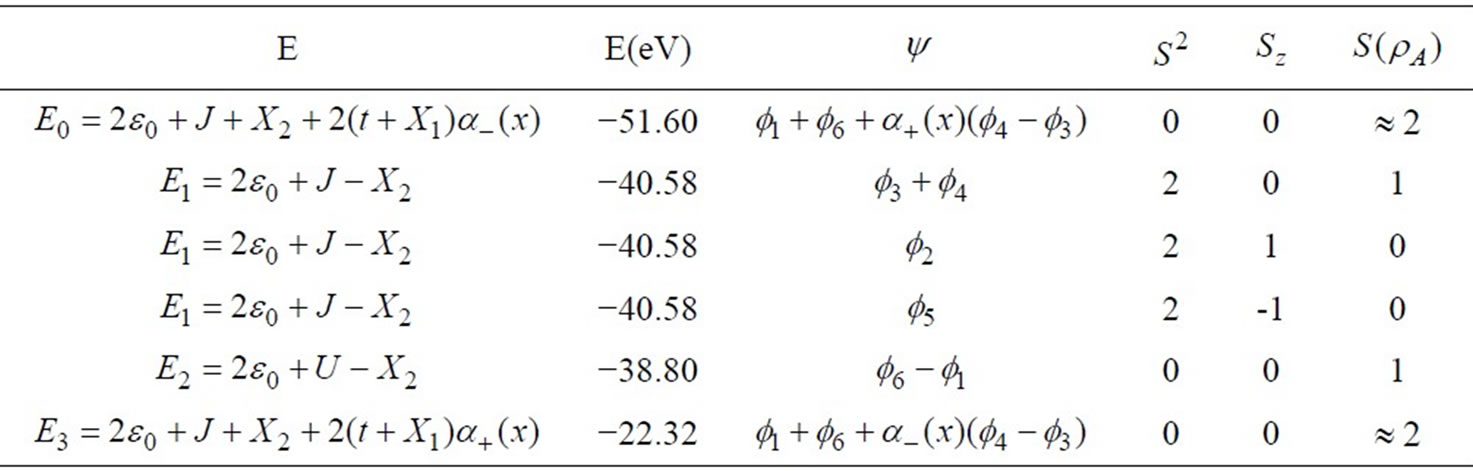
Table 2. The parametric energies of hydrogen molecule are listed in the first column of the Table, where 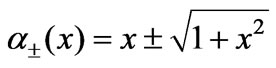 and
and . The values of energies from [22] are listed in the second column, eigenfunction for these states are also listed in the third column. The S2 and Sz of each state are given in the next columns and the last column is the calculated entanglement
. The values of energies from [22] are listed in the second column, eigenfunction for these states are also listed in the third column. The S2 and Sz of each state are given in the next columns and the last column is the calculated entanglement 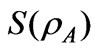 for these states, based on Zanardi’s measurement.
for these states, based on Zanardi’s measurement.
which  and
and  have S2 = 0, but
have S2 = 0, but 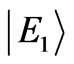 has S2 = 2. Some of the eigenvalues and eigenstates of hydrogen molecule are dependent to parameters of Hamiltonian via
has S2 = 2. Some of the eigenvalues and eigenstates of hydrogen molecule are dependent to parameters of Hamiltonian via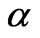 , where
, where 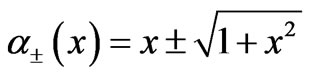 and
and
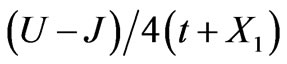
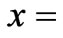 . All eigenvalues and S2, eigenstates (not normalized) and also their related Sz are summarized in Table 2.
. All eigenvalues and S2, eigenstates (not normalized) and also their related Sz are summarized in Table 2.
3. Results and Discussion
Based on the results summarized in Table 2 the wavefunction of the ground and third excited state are dependent upon e-e correlation parameters via 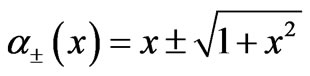 with
with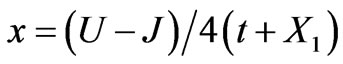 . Both of these states are nonmagnetic (S = 0). The wavefunctions of the first and second excited states are explicitly independent from Hamiltonian parameters. There is no dependency of any wavefunction to exchange interaction X2. Using parameters of Table 1 and von Neumann’s entropy given by Equation (6) an entanglement value of
. Both of these states are nonmagnetic (S = 0). The wavefunctions of the first and second excited states are explicitly independent from Hamiltonian parameters. There is no dependency of any wavefunction to exchange interaction X2. Using parameters of Table 1 and von Neumann’s entropy given by Equation (6) an entanglement value of 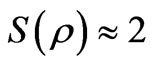 was obtained for ground and third excited states. The maximum available value of entanglement is
was obtained for ground and third excited states. The maximum available value of entanglement is 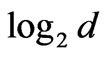 for a system with the Hilbert space dimension of the smaller subsystem as d [23]. Accordingly, for H2 molecule the maximum available entanglement is 2 and much closed values were obtained for these states. The results of maximally entangled ground and third excited states can be explained by the corresponding wave functions of these states. The wavefunctions of the ground and third excited states are superposition of four body basis of the systems i.e.
for a system with the Hilbert space dimension of the smaller subsystem as d [23]. Accordingly, for H2 molecule the maximum available entanglement is 2 and much closed values were obtained for these states. The results of maximally entangled ground and third excited states can be explained by the corresponding wave functions of these states. The wavefunctions of the ground and third excited states are superposition of four body basis of the systems i.e. 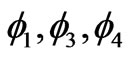 and
and  with equal coefficients since the value of
with equal coefficients since the value of 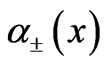 become 1 by considering the values of Table 1, therefore is maximum mixing and hence maximum entanglement. From Table 2, one can realize that the first excited state
become 1 by considering the values of Table 1, therefore is maximum mixing and hence maximum entanglement. From Table 2, one can realize that the first excited state 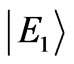 is a spin triplet state with S = 1 and its wavefunction is independent from correlation parameters. The value of entanglement for the Sz = 0 eigenfunction is 1 while its value for the eigenfunction with Sz = ±1 is zero. The difference between entanglements of the degenerate wavefunctions with different Sz can be explained by their related wavefunctions. The
is a spin triplet state with S = 1 and its wavefunction is independent from correlation parameters. The value of entanglement for the Sz = 0 eigenfunction is 1 while its value for the eigenfunction with Sz = ±1 is zero. The difference between entanglements of the degenerate wavefunctions with different Sz can be explained by their related wavefunctions. The 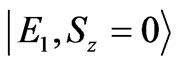 state is a linear combination of
state is a linear combination of 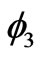 and
and 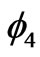 whereas the
whereas the 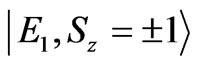 state are separable (
state are separable (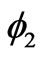 or
or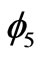 ). The importance of the nonzero spin of the first excited state is that this kind of state can be detected by Electron Paramagnetic Resonance (EPR) under some condition [24]. When the magnetic field is absent the wavefunction is a superposition of the degenerate wavefunctions with different Sz values. The calculated entanglement of this degenerate state is zero. However, after switching on the magnetic field, a wavefunction with distinct value of entanglement emerges. According to Table 2 the values of the Sz and entanglement for this state are 0 and 1 respectively. This might be a way for switching to a pure entangled state.
). The importance of the nonzero spin of the first excited state is that this kind of state can be detected by Electron Paramagnetic Resonance (EPR) under some condition [24]. When the magnetic field is absent the wavefunction is a superposition of the degenerate wavefunctions with different Sz values. The calculated entanglement of this degenerate state is zero. However, after switching on the magnetic field, a wavefunction with distinct value of entanglement emerges. According to Table 2 the values of the Sz and entanglement for this state are 0 and 1 respectively. This might be a way for switching to a pure entangled state.
The second excited state 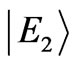 is nonmagnetic, S = 0, where the wavefunction is independent from correlation parameters. The calculated entanglement is 1. The wavefunction of this state is only a linear combination of two basis set
is nonmagnetic, S = 0, where the wavefunction is independent from correlation parameters. The calculated entanglement is 1. The wavefunction of this state is only a linear combination of two basis set 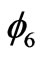 and
and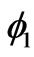 , hence its entanglement is smaller than ground and third excited states. By comparing the values of the entanglement listed in Table 2, one can conclude that the nonmagnetic states (S = 0) in which the wavefunction depend on interaction parameters are maximally entangled and the magnetic states whose wavefunctions are independent from correlation parameters are not entangled at all. Using von Neumann’s entropy given by Equation (6), the variation of entanglement for the ground state of H2 molecule with respect to the combination of correlation parameters
, hence its entanglement is smaller than ground and third excited states. By comparing the values of the entanglement listed in Table 2, one can conclude that the nonmagnetic states (S = 0) in which the wavefunction depend on interaction parameters are maximally entangled and the magnetic states whose wavefunctions are independent from correlation parameters are not entangled at all. Using von Neumann’s entropy given by Equation (6), the variation of entanglement for the ground state of H2 molecule with respect to the combination of correlation parameters  were calculated and is plotted in figure 1. It is clear from this figure that the value of entanglement is maximum for x = 0 (U = J). This conclusion resolves the unphysical gesture previously reported by other groups [17,19,20] who obtained maximally entangled ground state with U = 0. The U = 0 result imply that the maximally entangled ground state is not attainable for the H2 molecule since the ab initio value of U is 11.8 (Table 1), which is very far from zero. But the conclusion of our model indicates that the maximally entangled ground state is for U = J. This has a meaningful physical interpretation which states that in such physical system where the inter-atomic distance is very small, the on-site Columbic repulsion U can be very close to the inter-site Columbic repulsion J. Indeed the H2 molecule is the best example of such systems when the inter-atomic distance is minimum or d = 0.7A, the ab initio value of U and J from Table 2 gives x = 0.06. Also by using Hubbard parameters of Table 1, we obtained x = 0.06 and this value of x gives maximally entangled ground state. The maximum entanglement value for x = 0.06 is 1.99. As is observable in Figure 1, for the extreme limit or U much greater than t, i.e. strongly correlated systems the entanglement becomes smaller and tends to 1. The non-magnetic property of this state sets a limit on minimum available entanglement for this state. This point can be explained by using eigenfunction listed in Table 2. For
were calculated and is plotted in figure 1. It is clear from this figure that the value of entanglement is maximum for x = 0 (U = J). This conclusion resolves the unphysical gesture previously reported by other groups [17,19,20] who obtained maximally entangled ground state with U = 0. The U = 0 result imply that the maximally entangled ground state is not attainable for the H2 molecule since the ab initio value of U is 11.8 (Table 1), which is very far from zero. But the conclusion of our model indicates that the maximally entangled ground state is for U = J. This has a meaningful physical interpretation which states that in such physical system where the inter-atomic distance is very small, the on-site Columbic repulsion U can be very close to the inter-site Columbic repulsion J. Indeed the H2 molecule is the best example of such systems when the inter-atomic distance is minimum or d = 0.7A, the ab initio value of U and J from Table 2 gives x = 0.06. Also by using Hubbard parameters of Table 1, we obtained x = 0.06 and this value of x gives maximally entangled ground state. The maximum entanglement value for x = 0.06 is 1.99. As is observable in Figure 1, for the extreme limit or U much greater than t, i.e. strongly correlated systems the entanglement becomes smaller and tends to 1. The non-magnetic property of this state sets a limit on minimum available entanglement for this state. This point can be explained by using eigenfunction listed in Table 2. For 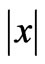 much greater than 1, one of the
much greater than 1, one of the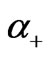 or
or 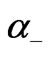 goes to zero and the other one becomes very large. In both cases the ground state wavefunctions listed in Table 2 reduce from extension over the four components to an extension over two components similar to
goes to zero and the other one becomes very large. In both cases the ground state wavefunctions listed in Table 2 reduce from extension over the four components to an extension over two components similar to 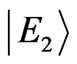 state. Therefore the corresponding value of entanglement reduces from 2 to 1. This also can be explained by tendency of the strongly correlated systems with U much greater than t to unpaired electronic configuration in atomic orbital such as
state. Therefore the corresponding value of entanglement reduces from 2 to 1. This also can be explained by tendency of the strongly correlated systems with U much greater than t to unpaired electronic configuration in atomic orbital such as 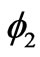 and
and 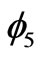 states. Such states tend to have parallel spin and as the result the entanglement reduces. In the case of H2 where the values of t, U and J are the same order of magnitude (See Table 1) and as the consequence x is much close to zero the molecule is in moderately correlated regime and one can obtain the maximum available entanglement as it is apparent in Figure 1. In this scheme both spatial and spin have to be considered for correlated wavefunction [17]. Neglecting exchange interaction in our model (X1 = X2 = 0), results to considerable change in energy levels of the system (see
states. Such states tend to have parallel spin and as the result the entanglement reduces. In the case of H2 where the values of t, U and J are the same order of magnitude (See Table 1) and as the consequence x is much close to zero the molecule is in moderately correlated regime and one can obtain the maximum available entanglement as it is apparent in Figure 1. In this scheme both spatial and spin have to be considered for correlated wavefunction [17]. Neglecting exchange interaction in our model (X1 = X2 = 0), results to considerable change in energy levels of the system (see
Table 2). However, the dependence of the ground and third excited state wavefunctions on the exchange parameters is only to X1 and putting X1 = 0 yields x = 0.07
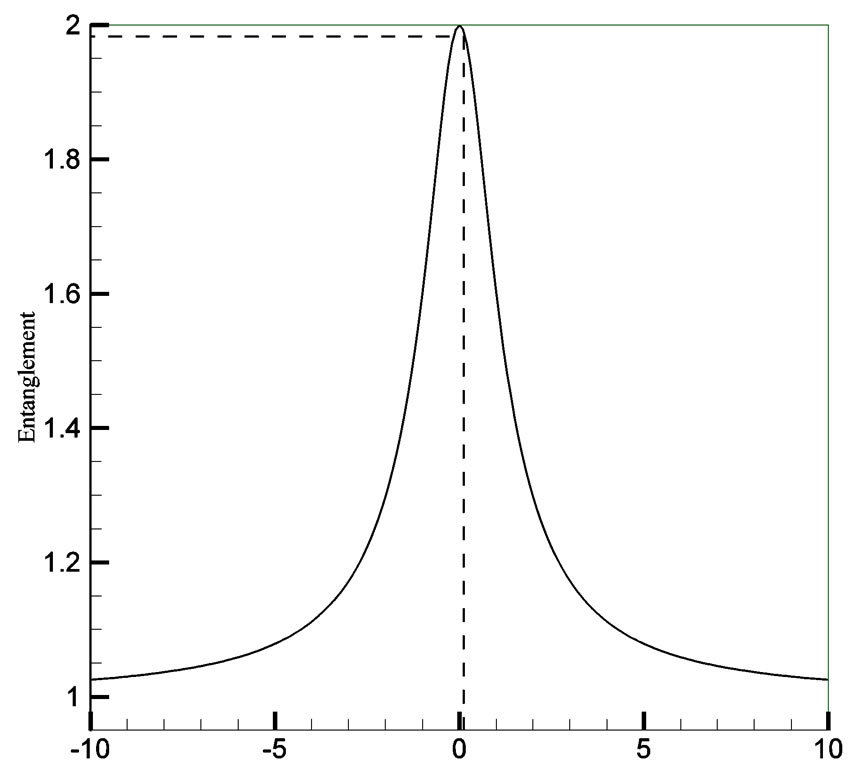
(U-J)/4(t+X1)
Figure 1. Entanglement for the ground state of Hydrogen molecule versus e-e interaction arameters.
and as the result the maximum entanglement becomes 1.99 which is the same as the case of nonzero X1 (x = 0.06). Hence in order to have maximally entangled states, the most effective parameters are direct Columbic interaction parameters U and J and exchange interaction parameters do not alter the value of entanglement significantly.
4. Conclusions
A many electron calculation on a simplest realistic two electron system i.e. H2 molecule was applied. Going beyond traditional Hubbard model lets to account correlation effects accurately in the many electron wavefunction of the ground and excited states. Using ab initio e-e interaction parameters gives a moderately correlated regime for the molecule and consequences maximally entangled ground and third excited state. The wavefunctions of the not magnetic (S = 0) ground and third excited states explicitly depend on correlation parameters whereas the first excited states which is magnetic (S2 = 2 and Sz  0) is not entangled. The second excited state is not magnetic but its wavefunction does not depend on correlation parameters therefore it is a moderately entangled state. In any case, by switching on a magnetic field an entangled state with Sz = 0 can be extracted from a not entangled degenerate magnetic state. We suggest that in a realistic molecular scale system, there is two criteria for finding maximally entangled electronic states, first the system should be in moderately correlated regime and second the system should have a non-magnetic (Sz = 0) electronic state.
0) is not entangled. The second excited state is not magnetic but its wavefunction does not depend on correlation parameters therefore it is a moderately entangled state. In any case, by switching on a magnetic field an entangled state with Sz = 0 can be extracted from a not entangled degenerate magnetic state. We suggest that in a realistic molecular scale system, there is two criteria for finding maximally entangled electronic states, first the system should be in moderately correlated regime and second the system should have a non-magnetic (Sz = 0) electronic state.
REFERENCES
- A. Einstein, B. Podolsky and N. Rosen, “Can Quantum-Mechanical Description of Physical Reality Be Considered Complete?” Physical Review, Vol. 47, No. 10, 1935, pp. 777-780. doi:10.1103/PhysRev.47.777
- E. Schrödinger, “Discussion of Probability Relations between Separated Systems,” Proceedings of the Cambridge Philosophical Society, Vol. 31, No. 4, 1935, pp. 555-563. doi:10.1017/S0305004100013554
- R. Horodecki, P. Horodecki, M. Horodecki and K. Horodecki, “Quantum Entanglement,” Reviews of Modern Physics, Vol. 81, No. 2, 2009, pp. 865-942. doi:10.1103/RevModPhys.81.865
- C. H. Bennett, G. Brassard, C. Crépeau, R. Jozsa, A. Peres and W. K. Wootters, “Teleporting an Unknown Quantum State via Dual Classical and Einstein-Podolsky-Rosen Channels,” Physical Review Letters, Vol. 70, No. 13, 1993, pp. 1895-1899. doi:10.1103/PhysRevLett.70.1895
- D. Bouwmeester, J. W. Pan, K. Mattle, M. Eibl, H. Weinfurter and A. Zeilinger, “Experimental Quantum Teleportation,” Nature, Vol. 390, 1997, pp. 575-579. doi:10.1038/37539
- C. H. Bennett and S. J. Wiesner, “Communication via Oneand Two-Particle Operators on Einstein-Podolsky-Rosen States,” Physical Review Letters, Vol. 69, No. 20, 1992, pp. 2881-2884. doi:10.1103/PhysRevLett.69.2881
- A. K. Ekert, “Quantum Cryptography Based on Bell’s Theorem,” Physical Review Letters, Vol. 67, No. 6, 1991, pp. 661-663. doi:10.1103/PhysRevLett.67.661
- C. A. Fuchs, “Nonorthogonal Quantum States Maximize Classical Information Capacity,” Physical Review Letters, Vol. 79, No. 6, 1997, pp. 1162-1165. doi:10.1103/PhysRevLett.79.1162
- Z. Huang and S. Kias, “Entanglement as Measure of Electron-Electron Correlation in Quantum Chemistry Calculations,” Chemical Physics Letters, Vol. 413, No. 1-3, 2005, pp. 1-5. doi:10.1016/j.cplett.2005.07.045
- T. A. C. Maiolo, F. della Sala, L. Martina and G. Soliani, “Entanglement of Electrons in Interacting Molecules,” Theoretical and Mathematical Physics, Vol. 152, No. 2, 2007, pp. 1146-1159. doi:10.1007/s11232-007-0098-9
- Y. S. Li, B. Zeng, X. S. Liu and G. L. Long, “Entanglement in a Two-Identical-Particle System,” Physical Review A, Vol. 64, No. 5, 2001, Article ID: 054302-1-4. doi:10.1103/PhysRevA.64.054302
- W. K. Wootters, “Entanglement of Formation of an Arbitrary State of Two Qubits,” Physical Review Letters, Vol. 80, No. 10, 1998, pp. 2245-2248. doi:10.1103/PhysRevLett.80.2245
- J. Schliemann, D. Loss and A. H. MacDonald, “Double-Occupancy Errors, Adiabaticity, and Entanglement of Spin Qubits in Quantum Dots,” Physical Review B, Vol. 63, No. 8, 2001, Article ID: 085311-1-8. doi:10.1103/PhysRevB.63.085311
- J. Schliemann, J. Ignacio Cirac, M. Kus, M. Lewenstein and D. Loss, “Quantum Correlations in Two-Fermion Systems,” Physical Review A, Vol. 64, No. 2, 2001, Article ID: 022303-1-9.
- J. R. Gittings and A. J. Fisher, “Describing Mixed SpinSpace Entanglement of Pure States of Indistinguishable Particles Using an Occupation-Number Basis,” Physical Review A, Vol. 66, No. 3, 2002, Article ID: 032305-1-11. doi:10.1103/PhysRevA.66.032305
- P. Zanardi, “Bipartite Mode Entanglement of Bosonic Condensates on Tunneling Graphs,” Physical Review A, Vol. 67, No. 5, 2003, Article ID: 054301-1-4. doi:10.1103/PhysRevA.67.054301
- P. Zanardi, “Quantum Entanglement in Fermionic Lattices,” Physical Review A, Vol. 65, No. 4, 2002, Article ID: 042101-1-5. doi:10.1103/PhysRevA.65.042101
- B. Alvarez-Fernández and J. A. Blanco, “The Hubbard Model for the Hydrogen Molecule,” European Journal of Physics, Vol. 23, No. 1, 2002, pp. 11-16. doi:10.1088/0143-0807/23/1/302
- H. Wang and S. Kias, “Quantum Teleportation in OneDimensional Quantum Dots System,” Chemical Physics Letters, Vol. 421, No. 4-6, 2006, p. 338. doi:10.1016/j.cplett.2006.01.093
- S.-J. Gu, S.-S. Deng, Y.-Q. Li and H.-Q. Lin, “Entanglement and Quantum Phase Transition in the Extended Hubbard Model,” Physical Review Letters, Vol. 93, No. 8, 2004, Article ID: 086402-1-4. doi:10.1103/PhysRevLett.93.086402
- M. H. Saani, M. A. Vesaghi, K. Esfarjani, T. G. Elahi, M. Sayari, H. Hashemi and N. Gorjizadeh, “Lattice Relaxation in Many-Electron States of the Diamond Vacancy,” Physical Review B, Vol. 71, No. 3, 2005, Article ID: 035202-1-9.
- G. Chiappe, E. Louis, E. SanFabian and J. A. Verges, “Hubbard Hamiltonian for the Hydrogen Molecule,” Physical Review B, Vol. 75, No. 19, 2007, Article ID: 195104-1-6. doi:10.1103/PhysRevB.75.195104
- C. H. Bennett, H. J. Bernstein, S. Popescu and B. Schumacher, “Concentrating Partial Entanglement by Local Operations,” Physical Review A, Vol. 53, No. 4, 1996, pp. 2046-2052. doi:10.1103/PhysRevA.53.2046
- J. A. Vanwyk, O. D. Tucker, M. E. Newton, J. M. Baker, G. S. Woods and P. Spear, “Magnetic-Resonance Measurements on the 5A2 Excited State of the Neutral Vacancy in Diamond,” Physical Review B, Vol. 52, No. 17, 1995, pp. 12657-12667. doi:10.1103/PhysRevB.52.12657

