ABSTRACT

In this paper, verification of real-time pricing systems of electricity is considered using a probabilistic Boolean network (PBN). In real-time pricing systems, electricity conservation is achieved by manipulating the electricity price at each time. A PBN is widely used as a model of complex systems, and is appropriate as a model of real- time pricing systems. Using the PBN-based model, real-time pricing systems can be quantitatively analyzed. In this paper, we propose a verification method of real-time pricing systems using the PBN-based model and the probabilistic model checker PRISM. First, the PBN-based model is derived. Next, the reachability problem, which is one of the typical verification problems, is formulated, and a solution method is derived. Finally, the effectiveness of the proposed method is presented by a numerical example.

Keywords:

Model Checking, Probabilistic Boolean Networks, Real-Time Pricing

1. Introduction

In recent years, there has been growing interest in energy and the environment. For problems on energy and the environment such as energy saving, several approaches have been studied (see, e.g., [1] [2] ). In this paper, we focus on real-time pricing systems of electricity. A real-time pricing system of electricity is a system that charges different electricity prices for different hours of the day and for different days, and is effective for reducing the peak and flattening the load curve (see, e.g., [3] - [6] ). In general, a real-time pricing system consists of one controller deciding the price at each time and multiple electric consumers such as commercial facilities and homes. If electricity conservation is needed, then the price is set to a high value. Since the economic load becomes high, consumers conserve electricity. Thus, electricity conservation is achieved. In the existing methods, the price at each time is given by a simple function with respect to power consumptions and voltage deviations and so on (see, e.g., [6] ). In order to realize more precisely pricing, it is necessary to use a mathematical model of consumers.

On the other hand, in order to deal with complex systems such as power systems and gene regulatory networks, it is one of the appropriate methods to approximate a complex system by a discrete abstract model (see, e.g., [7] ). In addition, human decision making is also complex, and is modeled by a discrete model (see, e.g., [8] ). Thus, in analysis and control of complex systems and those with human decision making, a discrete model plays an important role. Several discrete models have been proposed so far (see, e.g., [9] ). In this paper, we focus on a Boolean network (BN) [10] . In a BN, the state is given by a binary value (0 or 1), and the dynamics are expressed by a set of Boolean functions. Since Boolean functions are used, it is easy to understand the interaction between states. In addition, the behavior of complex systems is frequently stochastic by the effects of noise. From this viewpoint, a probabilistic BN (PBN) has been proposed in [11] . In a PBN, a Boolean function is randomly decided at each time among the candidates of Boolean functions.

Under the above backgrounds, the authors have proposed in [12] the PBN-based model of real-time pricing systems. In this model, decision making of electric consumers is modeled by a PBN. That is, decisions of a consumer are modeled by Boolean functions, and one of decisions is selected probabilistically. Selection probabilities are controlled by the price at each time. In [12] , an approximate algorithm for solving the optimal control problem has been proposed. However, analysis and verification using the PBN-based model have not been considered.

In this paper, we propose a verification method of real-time pricing systems using the PBN-based model and the probabilistic model checker PRISM [13] . Using PRISM, we can verify whether this system satisfies the specification described by probabilistic computation tree logic (PCTL) [14] or not. The reachability problem is considered as one of the typical verification problems, and a numerical example is presented. The proposed method provides us a basic of model-based design of real-time pricing systems.

In Section 2, the outline of real-time pricing systems studied in this paper is explained. In Section 3, the PBN-based model is explained. In Section 4, the verification problem is formulated. In Section 5, a solution method using PRISM is proposed. In Section 6, a numerical example is presented. In Section 7, we conclude this paper.

Notation: For the n-dimensional vector 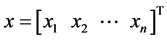and the index set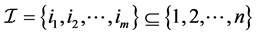, 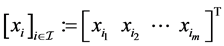is defined.

2 Real-Time Pricing Systems

In this section, we explain the outline of real-time pricing systems studied in this paper.

Figure 1 shows an illustration of real-time pricing systems studied in this paper. This system consists of one controller and multiple electric consumers such as commercial facilities and homes. For an electric consumer, we suppose that each consumer can

monitor the status of electricity conservation of other consumers. In other words, the status of some consumer affects that of other consumers. For example, in commercial facilities, we suppose that the status of rival commercial facilities can be checked by lighting, Blog, Twitter, and so on. Depending on power consumption, i.e., the status of electricity conservation, the controller determines the price at each time. If electricity conservation is needed, then the price is set to a high value. Since the economic load becomes high, consumers conserve electricity. Thus, electricity conservation is achieved. The price does not depend on each consumer, and is uniquely determined.

In this paper, decision making of electric consumers is modeled by a probabilistic Boolean network (PBN). Here, we suppose that each electric consumer has candidates of a decision in electricity conservation, and one of candidates is selected probabilistically depending on the electricity price at the current time. In such a case, it is appropriate to adopt the PBN-based model. In this paper, the property of real-time pricing systems can be verified using the PBN-based model.

3. Modeling Using Probabilistic Boolean Networks

In this section, first, we explain the outline of PBNs. Next, each consumer in real-time pricing systems is modeled by a PBN.

3.1. Probabilistic Boolean Networks

First, we explain a (deterministic) Boolean network (BN). A BN is defined by

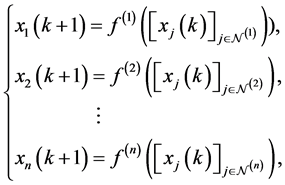(1)

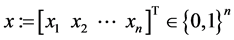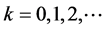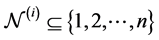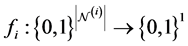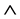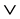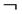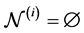where is the state, and is the discrete time. The set is a given index set, and the function is a given Boolean function consisting of logical operators such as AND (), OR (), and NOT (). If holds, then 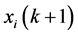is uniquely determined as 0 or 1.

Next, we explain a probabilistic Boolean network (PBN) (see [11] for further details). In a PBN, the candidates of 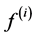are given, and for each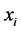, selecting one Boolean function is probabilistically independent at each time. Let

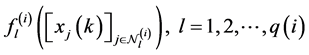
denote the candidates of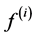. The probability that is selected is defined by

Then, the following relation

(2)

must be satisfied. Probabilistic distributions are derived from experimental results. Finally, , are defined by

We show a simple example.

Example 1. Consider the PBN in which Boolean functions and probabilities are given by

where, and hold, , , and hold, and we see that the relation (2) is satisfied. Next, consider the state trajectory. Then, for, we can obtain

In this example, the cardinality of the finite state set is given by, and we obtain the state transition diagram of Figure 2 by computing the transition from each state. In Figure 2, the number assigned to each node denotes, , (elements of the state), and the number assigned to each arc denotes the transition probability from some state to other state. Note here that for simplicity, the state transition from only is illustrated in Figure 2. ,

3.2. Model of Consumers

Consider modeling the set of consumers as a PBN. The number of consumers is given by n. We assume that the state of consumer is binary, and is denoted by. The state implies

The binary value of is determined by power consumption of consumer i. In addition, we assume that the probability is time-varying and is changed by the price at each time. That is, the probability is given by

where is the price (the control input). We assume that the set is a finite set, and for any, two conditions (2) and hold. The Boolean function must be derived depending on real situations and experimental results. In this paper, as one of examples, we consider the following situation, which will mimic a real situation.

Let, denote the set of consumers, which affect to consumer i. We assume that there exists one leader in the local area. The state of a leader is given by. Then, for consumer i, we consider the following model:

(3)

The Boolean functions and imply that consumer i forcibly conserves (or does not conserve) electricity. In these cases, time evolution of the state does not depend on the past state. The Boolean function implies that the state is not changed. The Boolean function implies that the state of consumer i is changed depending on the other consumers. The Boolean function implies that the state of consumer i is changed depending on the leader. Thus, decision making of consumers can be modeled by a PBN. Of course, we may use other Boolean functions.

4. Problem Formulation

In this section, the verification problem described by probabilistic computation tree logic (PCTL) is formulated for the PBN-based model of consumers (see Appendix A for details on PCTL).

Here, the reachability problem is formulated as one of the typical problems. For the system, given by (3), the output is defined, where,. We remark that the output is not the measured signal. First, the reachability problem is given.

Problem 1. Suppose that for the system, given by (3), the initial state, the control time N, and the target output are given. Then, find a maximum probability p satisfying

by manipulating a control input sequence.

Let denote the maximum probability obtained by solving this problem. In this problem, we find a maximum probability that holds within time N. In the conventional reachability problem, only terminal time is focused, and it is checked whether holds or not. In this paper, we focus on not only terminal time N but also other times. Since the system has the control input, we find a maximum probability satisfying the condition. In the case where peak demand is focused on, may be replaced with, where is a given constant.

Furthermore, by solving Problem 1 at each time, a kind of model predictive control (MPC) can be realized (see Section 5.3 for further details).

5. Solution Method Using PRISM

In this section, we consider a solution method for Problem 1 using the probabilistic model checker PRISM [13] .

5.1. Preparation: Transformation of Boolean Functions

As a preparation, the following lemma [15] is introduced.

Lemma 1. Consider two binary variables. Then the following relations hold.

i) is equivalent to.

ii) is equivalent to.

iii) is equivalent to.

For example, is equivalently transformed into . By using this lemma, a Boolean function can be transformed into a polynomial with binary variables.

5.2. Description in PRISM

To solve Problem 1 and the verification problem described by PCTL formulas, the probabilistic model checker PRISM is used. PRISM supports a discrete-time Markov chain (DT-MC), a continuous-time Markov chain (CT-MC), and a Markov decision process (MDP). PRISM consists of three parts: “Model”, “Properties”, “Simulator”. In the “Model” part, a given probabilistic system is described using the PRISM language. In the “Properties” part, the property specification language incorporates temporal logic such as PCTL, and we can verify whether a given PCTL formula holds or not. In the “Simulator”, the state trajectories can be simulated.

Using PRISM, consider modeling the system, given by (3). To explain the PRISM-based method, consider the following model of three consumers:

In addition, is given by. Then, the PRISM source code describing this system is shown as follows.

01: mdp

02: module RTP1

03: x1: [0..1] init 1;

04: [RTP] u=3 -> 0.1:(x1’=1) + 0.075:(x1’=0) + 0.6:(x1’=x1) + 0.15:(x1’=x2*x3)

+ 0.075:(x1’=x1)

05: [RTP] u=4 -> 0.1:(x1’=1) + 0.1:(x1’=0) + 0.5:(x1’=x1) + 0.2:(x1’=x2*x3)

+ 0.1:(x1’=x1)

06: [RTP] u=5 -> 0.1:(x1’=1) + 0.125:(x1’=0) + 0.4:(x1’=x1) + 0.25:(x1’=x2*x3)

+ 0.125:(x1’=x1)

07: endmodule

08: module RTP2

09: x2:[0..1] init 1;

10: [RTP] u=3 -> 0.1:(x2’=1) + 0.075:(x2’=0) + 0.6:(x2’=x2) + 0.15:(x2’=x1*x3)

+ 0.075:(x2’=x1)

11: [RTP] u=4 -> 0.1:(x2’=1) + ... (omit)

12: [RTP] u=5 -> 0.1:(x2’=1) + ... (omit)

13: endmodule

14: module RTP3

15: x3:[0..1] init 1;

16: [RTP] u=3 -> 0.1:(x3’=1) + 0.075:(x3’=0) + 0.6:(x3’=x3) + 0.15:(x3’=x1*x2)

+ 0.075:(x3’=x1)

17: [RTP] u=4 -> 0.1:(x3’=1) + ... (omit)

18: [RTP] u=5 -> 0.1:(x3’=1) + ... (omit)

19: endmodule

20: module input

21: u:[3..5] init 3;

22: [RTP] u=3 -> (u’=3);

23: [RTP] u=3 -> (u’=4);

24: [RTP] u=3 -> (u’=5);

25: [RTP] u=4 -> (u’=3);

26: [RTP] u=4 -> (u’=4);

27: [RTP] u=4 -> (u’=5);

28: [RTP] u=5 -> (u’=3);

29: [RTP] u=5 -> (u’=4);

30: [RTP] u=5 -> (u’=5);

31: endmodule.

In line 1, it is described that a given system is an MDP, i.e., the control input (in other words, the nondeterministic variable) that must decide is included. In lines 2-7, the dynamics for (consumer 1) are modeled. In line 3, it is described that takes a binary value, and the initial value of is given by. In line 4, if holds, then the value of at the next time is given by 1 with the probability 0.1, 0 with the probability 0.075, (i.e., the state is not changed) with the probability 0.6, (corresponding to ¹) with the probability 0.15, and with the probability 0.15. Similarly, in line 5, the case of is described. In line 6, the case of is described. In lines 8-13, the dynamics for (consumer 2) are modeled. In lines 14-19, the dynamics for (consumer 3) are modeled. In this system, a discrete probabilistic distribution is given for each. Hence, in PRISM, the dynamics for each must be modeled separately. In lines 20-31, the property of the control input is described as a nondeterministic variable. We note here that the initial value of the control input must be given (see line 21). Finally, to associate with each module, [RTP] is described in lines 4-6, 10-12, 16-18, 22-30.

From the above example, we see that the system, given by (3) can be described by PRISM. Finally, we present a procedure for deriving the PRISM source code as follows. In the following procedure, without loss of generality, the input set is given by.

Derivation Procedure of PRISM Source Code:

Step 1: Transform each Boolean function into a polynomial with binary variables by using Lemma 1. Let denote the obtained polynomial.

Step 2: Describe that a given system is an MDP.

Step 3: Compute the probability for each element of. Let denote the probability for.

Step 4: Describe module RTP i, as follows.

module RTP i;

: init;

[RTP];

[RTP];

endmodule.

Step 5: Describe the control input u as follows.

module input

u: init;

[RTP];

[RTP];

[RTP];

[RTP];

endmodule.

The above procedure is the improved version of the procedure proposed in [16] .

5.3. Verification and Application to MPC

Several properties described by PCTL formulas can be verified by using the obtained model on PRISM. We use the “Properties” part in PRISM.

Consider solving Problem 1 (the reachability problem). Then, we use P_max prepared in PRISM. Suppose and. Then in PRISM, this problem is described by

This implies that find a maximum probability satisfying the following condition: at time, the number of times that holds is greater than or equal to 1, i.e., this code expresses the reachability problem itself.

From the above results, we see that the verification problem can be easily implemented by using PRISM. The control input sequence is obtained simultaneously, but in PRISM 4.0.3, the obtained control input sequence cannot be displayed except for the case of. In the case of, the discrete-time Markov chain can be obtained as the closed-loop system of a given system. The control input sequence can be obtained by exploratory analysis using the simulator in PRISM. Otherwise, this sequence can be obtained by solving the control problem such as the optimal control problem. In both cases, the verification result will be useful.

On the other hand, the problem of finding and a control input sequence can be regarded as a kind of the control problem. Noting that the initial value of the control input must be given, a kind of MPC can be realized by the following procedure.

[Procedure of MPC]

Step 1: Set, and determine the current state according to power consumption.

Step 2: Find the current control input maximizing. That is, for each, solve Problem 1.

Step 3: Apply only the control input at t, i.e., , to the plant.

Step 4: Set, determine according to power consumption, and go to Step 2.

6. Numerical Example

We present a numerical example. For, given by (3), parameters are given as follows:

We remark that for any, two conditions (2) and hold. The Boolean function is given by

In Problem 1, the control time N, the output, and the target output are given by

In this example, we consider the following cases:

・ Case 1: The initial state is given by (all consumers normally use electricity).

Case 1-1: The initial input is given by.

Case 1-2: The initial input is given by.

・ Case 2: The initial state is given by and, (only consumer 4 conserves electricity).

Case 2-1: The initial input is given by.

Case 2-2: The initial input is given by.

・ Case 3: The initial state is given by and, (only consumer 1 (leader) conserves electricity).

Case 3-1: The initial input is given by.

Case 3-2: The initial input is given by.

Next, we present the computation result. Table 1 shows for each case. By checking, we can verify the status of electricity conservation. If is large, then there is a trend that consumers conserve electricity. From Table 1, we see the following facts:

1) It is desirable that the initial input (price) is given by.

2) Even if one consumer, who is not the leader, conserves electricity, then a contribution to electricity conservation is small.

3) If the leader conserves electricity, then a contribution to electricity conservation is large.

Thus, using the PBN-based model, we can analyze real-time pricing systems in a quantitative way.

7. Conclusions

In this paper, using a probabilistic Boolean network (PBN), we discussed verification of

real-time pricing systems of electricity. The PBN-based model and PRISM enable us an easy and convenient verification. As one of the verification problems, the reachability problem was considered. In addition, application to model predictive control was also discussed. The proposed method provides us verification/control methods for real-time pricing systems.

There are several open problems. It is significant to develop the identification method of Boolean functions and parameters in (3). Once Boolean functions and parameters can be obtained, the proposed method enables us quantitative analysis. Furthermore, for large-scale systems, there is a possibility that PRISM does not work. In such a case, we may use the assume-guarantee verification technique [17] , which is one of the compositional verification techniques. Details are one of the future efforts. It is also significant to consider extending a PBN to a probabilistic system with multi-valued logic functions (see e.g., [18] - [21] for further details about such probabilistic systems). Since the PBN-based model expresses human decision making in the purchasing behavior, the proposed method is related to analysis of the consumer behavior in economics. It is important to clarify the relation between the proposed method and the existing method in economics. The proposed method is the first step toward mathematical analysis of the consumer behavior.

Acknowledgements

This research was partly supported by JST, CREST and Grant-in-Aid for Scientific Research (C) 26420412.

Cite this paper

Kobayashi, K. and Hiraishi, K. (2016) Verification of Real-Time Pricing Systems Based on Probabilistic Boolean Networks. Applied Mathematics, 7, 1734- 1747. http://dx.doi.org/10.4236/am.2016.715146

References

Appendix A. Probabilistic Computation Tree Logic

In classical propositional logic, truth-value of 0 (false) or 1 (true) is time-invariant. Temporal logic is an extension of propositional logic, and deals with time evolution of truth-value. Since a PBN is a discrete-time system, we also consider temporal logic in discrete-time. First, computation tree logic (CTL) is explained as a class of temporal logics. Next, we introduce probabilistic CTL (PCTL) (see [14] for further details).

In CTL, logical operators and temporal operators are used. The logical operators usually consist of, , , , and. The temporal operators consists of quantifiers over paths A, E and path-specific quantifiers F, G, X, U. CTL formulas, state formulas, and path formulas are defined as follows:

1) Propositional variables and propositional constants (true or false) are state formulas.

2) If f, y are state formulas, then, , , , and are also state formulas.

3) If f is path formula, then Ef and Af are state formulas.

4) If f, y are state formulas, then Xf, Ff, Gf, and fUy are path formulas.

5) All state and path formulas consist of the above formulas, and all CTL formulas consist of state formulas.

Next, suppose that are given as propositional variables. Then the meaning of each quantifier over paths is explained as follows:

・ Af: f has to hold on all paths starting from the current state (All).

・ Ef: there exists at least one path starting from the current state where f holds (Exists).

Furthermore, the meaning of each path-specific quantifier is also explained as follows:

・ Ff: f eventually has to hold (somewhere on the subsequent path) (Finally).

・ Gf: f has to hold on the entire subsequent path (Globally).

・ Xf: f has to hold at the next state (neXt).

・ fUy: f has to hold until at some position y holds. This implies that y will be verified in the future.

In PCTL, the notion of probability is added in CTL, that is, for the CTL formula f, consider, ,. For example, implies that if f is true with the probability that is less than or equal to p, then is true, otherwise is false.

Finally, the temporal operator F is improved to F^£N. For the propositional variable f, F^£Nf implies that f eventually has to hold until time N.

¹In PRISM, given Boolean functions may be directly used (see http://www.prismmodelchecker.org/ for further details).