ABSTRACT

This paper is concerned with the stability analysis of nonlinear third order ordinary differential equations of the form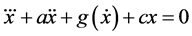. We construct a suitable Lyapunov function for this purpose and show that it guarantees asymptotic stability. Our approach is to first consider the linear version of the above ODE, by taking 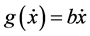and study its Lyapunov stability. Exploiting the similarities between linear and nonlinear ODE, we construct a Lyapunov function for the stability analysis of the given nonlinear differential equation.

Keywords:

Nonlinear ODE, Energy, Lyapunov Function, Assymptotic Stability

1. Introduction

In 1892, Lyapunov [1] proposed a fundamental method for studying the problem of stability by constructing functions known as Lyapunov functions. This function is often represented as 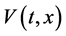defined in some region or the whole state phase that contains the unperturbed solution x = 0 for all t > 0 and which together with its derivative satisfy some sign definiteness. The following definitions of stability were given by Lyapunov.

1.1. Definition (Lyapunov)

Consider the system

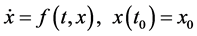(1)

where x denotes an n-dimensional vector and (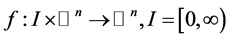) is continuous. Let 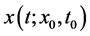be a solution of the Equation (1) through then the trivial solution 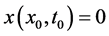of the system (1) is said to be stable at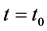, provided that for arbitrary positive, there exist a 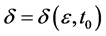such that whenever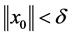, the inequality is satisfied for all.

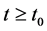1.2. Definition (Lyapunov)

The trivial solution 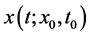of the system (1) is said to be asymptotically stable if it is stable, and for each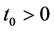, there is an such that implies as. If in addition all solutions tend to zero, then the trivial solution is asymptotically stable in the large.

1.3. Lyapunov’s Theorem on Stability (Lyapunov)

Suppose there is a function V which is positive definite along every trajectory of (1), and is such that the total derivative is semi definite of opposite sign (or identically zero) along the trajectory of (1). Then the perturbed motion is stable. If a function V exists with these properties and admits an infinitely small upper bound, and if is definite (with sign opposite of V), it can be shown further that every perturbed trajectory which is sufficiently close to the unperturbed motion approaches the latter asymptotically.

1.4. Remark

1) The basis of Lyapunov theory in simple terms is that; if the total energy is dissipated, then the system must be stable.

2) The main advantage of this approach is that; by looking at how an energy-like function V (Lyapunov function) changes over time, we might conclude that a system is stable or asymptotically stable without solving the differential equation.

3) The disadvantage of this approach is that; finding a Lyapunov function may not be so easy! [2] .

1.5. Motivation

1) Eigenvalue analysis concept does not hold good for nonlinear systems [1] [3] .

2) Nonlinear systems can have multiple equilibrium points and limit cycles [4] .

3) Stability behaviour of nonlinear systems need not always be global (unlike linear

systems) [5] [6] .

1.6. How Energy Is Associated with Dynamical Systems

We illustrate here how we can derive the Hamiltonian for a dynamical system of the form

(2)

The Hamiltonian of a system is the sum of its kinetic (T) and potential energies (V), i.e.

(3)

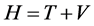
Given Equation (2), multiply by to get;

(4)

We observe that;

Hence substituting in (4) we get;

Integrating with respect to t,

The required Hamiltonian is;

(5)

1.7. Remark

1) Any dynamical system of the form is conservative [7] , i.e. the total energy of the system is conserved, and this implies that there exists a function H such

that, where H is the Hamiltonian of the system.

2) The function is often used as a Lyapunov function candi-

date in the stability analysis of many conservative systems.

3) A concrete example of a conservative system is the simple pendulum [8] .

1.8. Stability Definitions

We consider nonlinear time-invariant system, a point is an equilibrium point of the system if. We remark that is an equilibrium point if and only if is a trajectory. Figure 1 illustrates schematically the concept of stability and asymptotic stability with respect to an equilibrium point. Their definitions follow.

1.9. Definition

An equilibrium solution of is said to be:

1) stable if, given any and any, there exists a such that

2) uniformly stable if, for every, there exits, independent of, such that (3.3.1) is satisfied for all,

3) unstable if it is not stable.

4) asymptotically stable if there exists a such that

5) The system is globally asymptotically stable (G.A.S.) if for every trajectory and as (implies is the unique equilibrium point).

6) The system is locally asymptotically stable (L.A.S.) near or at if there is an s.t. as.

2. Construction of Lyapunov Function for Third Order Linear ODE

Ogundare [9] constructed a Lyapunov function for a second order linear system of ordinary differential equation using a quadratic form. We shall adapt his method with slightly more simplified assumptions to construct a Lyapunov function for a third order linear ODE of the form

(6)

which is equivalent to the system

(7)

where a, b, c are all positive constants. The required quadratic form in this case is given as

(8)

where A, B, C, D, E, and F are constants to be determined. Differentiating Equation (8) with respect to the system (7) we have

(9)

Setting the coefficients of to be zero and coefficient of greater than zero in Equation (9), we obtain

(10)

Solving the system we have,

(11)

By setting C = 1, we obtain

(12)

with, these values of the constants guarantee the positive definiteness of V and negative definiteness of its derivative. So, substituting (12) into Equation (8), gives

(13)

We now find the time derivative of V:

(14)

Equation (13) is positive definite with, and (14) negative definite, therefore, satisfies Lyapunov stability criteria.

2.1. Construction of Lyapunov Function for Third Order Nonlinear ODE

Exploiting the similarities between linear and nonlinear systems, we shall construct a Lyapunov function for the stability of third order nonlinear differential equation of the form;

(15)

Equation (15) is equivalent to the system

(16)

Taking into account the similarities between the linear and the nonlinear systems, we can see a close comparison with Equations (16) and (7), that has been replaced by

or, where.

We use Equation (13) as our trial Lyapunov function, given by

(17)

We also assume that

.

This implies that

(18)

Since, we have that

,

Hence V is positive definite.

Also, the time derivative of V along the solution path of (16)

(19)

Clearly is negative definite and we have asymptotic stability.

Therefore, the Lyapunov function;

,

is an appropriate Lyapunov function for the system (16).

2.2. Conclusion

We have seen that the Lyapunov function candidate constructed in this project is a good tool in the stability analysis of dynamical systems. Without the need to solve the systems of differential equations involved, we were able to obtain the qualitative behaviour of the systems near their equilibrium points.

Cite this paper

Okereke, R.N. (2016) Lyapunov Stability Analysis of Certain Third Order Nonlinear Differential Equations. Applied Mathematics, 7, 1971- 1977. http://dx.doi.org/10.4236/am.2016.716161

References