Received 10 May 2016; accepted 18 July 2016; published 21 July 2016

ABSTRACT

An important problem that arises in different areas of science and engineering is that of computing the limits of sequences of vectors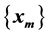, where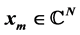, N being very large. Such sequences arise, for example, in the solution of systems of linear or nonlinear equations by fixed-point iterative methods, and 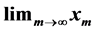are simply the required solutions. In most cases of interest, however, these sequences converge to their limits extremely slowly. One practical way to make the sequences converge more quickly is to apply to them vector extrapolation methods. Two types of methods exist in the literature: polynomial type methods and epsilon algorithms. In most applications, the polynomial type methods have proved to be superior convergence accelerators. Three polynomial type methods are known, and these are the minimal polynomial extrapolation (MPE), the reduced rank extrapolation (RRE), and the modified minimal polynomial extrapolation (MMPE). In this work, we develop yet another polynomial type method, which is based on the singular value decomposition, as well as the ideas that lead to MPE. We denote this new method by SVD-MPE. We also design a numerically stable algorithm for its implementation, whose computational cost and storage requirements are minimal. Finally, we illustrate the use of SVD-MPE with numerical examples.

Keywords:

Vector Extrapolation, Minimal Polynomial Extrapolation, Singular Value Decomposition, Krylov Subspace Methods

1. Introduction and Background

An important problem that arises in different areas of science and engineering is that of computing limits of sequences of vectors 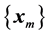1, where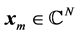, the dimension N being very large in many applications. Such vector sequences arise, for example, in the numerical solution of very large systems of linear or nonlinear equations by fixed-point iterative methods, and 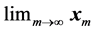are simply the required solutions to these systems. One common source of such systems is the finite-difference or finite-element discretization of continuum problems.

In most cases of interest, however, the sequences 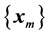converge to their limits extremely slowly. That is, to approximate, with a reasonable prescribed level of accuracy, by, we need to consider very large values of m. Since the vectors 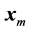are normally computed in the order 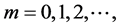it is clear that we have to compute many such vectors until we reach one that has acceptable accuracy. Thus, this way of app- roximating via the 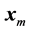becomes very expensive computationally.

Nevertheless, we may ask whether we can do something with those 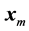that are already available, to somehow obtain new approximations to that are better than each individual available. The answer to this question is in the affirmative for at least a large class of sequences that arise from fixed-point iteration of linear and nonlinear systems of equations. One practical way of achieving this is by applying to the sequence a suitable convergence acceleration method (or extrapolation method).

Of course, in case does not exist, it seems that no use could be made of the. Now, if the sequence is generated by an iterative solution of a linear or nonlinear system of equations, it can be thought of as “diverging from” the solution of this system. We call the antilimit of in such a case. It turns out that vector extrapolation methods can be applied to such divergent sequences to obtain good approximations to the relevant antilimits, at least in some cases.

Two different types of vector extrapolation methods exist in the literature:

1) Polynomial type methods: The minimal polynomial extrapolation (MPE) of Cabay and Jackson [1] , the reduced rank extrapolation (RRE) of Kaniel and Stein [2] , Eddy [3] , and Mešina [4] , and the modified minimal polynomial extrapolation (MMPE) of Brezinski [5] , Pugachev [6] and Sidi, Ford, and Smith [7] .

2) Epsilon algorithms: The scalar epsilon algorithm (SEA) of Wynn [8] (which is actually a recursive procedure for implementing the transformation of Shanks [9] ), the vector epsilon algorithm (VEA) of Wynn [10] , and the topological epsilon algorithm (TEA) of Brezinski [5] .

The paper by Smith, Ford, and Sidi [11] gives a review of all these methods (except MMPE) that covers the developments in vector extrapolation methods until the end of the 1970s. For up-to-date reviews of MPE and RRE, see Sidi [12] and [13] . Numerically stable algorithms for implementing MPE and RRE are given in Sidi [14] , these algorithms being also economical both computationally and storagewise. Jbilou and Sadok [15] have developed an analogous algorithm for MMPE along the lines suggested in Sidi, Ford, and Smith [7] and Sidi [14] . For the convergence properties and error analyses of MPE, RRE, MMPE, and TEA, as these are applied to vector sequences generated by fixed-point iterative methods from linear systems, see the works by Sidi [16] - [18] , Sidi, Ford, and Smith [7] , Sidi and Bridger [19] , and Sidi and Shapira [20] [21] . VEA has been studied by Brezinski [22] [23] , Gekeler [24] , Wynn [25] [26] , and Graves-Morris [27] [28] .

Vector extrapolation methods are used effectively in various branches of science and engineering in acceler- ating the convergence of iterative methods that result from large sparse systems of equations.

All of these methods have the useful feature that their only input is the vector sequence whose convergence is to be accelerated, nothing else being needed. In most applications, however, the polynomial type methods, especially MPE and RRE, have proved to be superior convergence accelerators; they require much less computation than, and half as much storage as, the epsilon algorithms for the same accuracy.

In this work, we develop yet another polynomial type method, which is based on the singular value decomposition (SVD), as well as some ideas that lead to MPE. We denote this new method by SVD-MPE. We also design a numerically stable algorithm for its implementation, whose computational cost and storage requirements are minimal. The new method is described in the next section. In Section 3, we show how the error in the approximation produced by SVD-MPE can be estimated at zero cost in terms of the quantities already used in the construction of the approximation. In Section 4, we give a very efficient algorithm for implementing SVD-MPE. In Section 5, we derive determinant representations for the approximations produced by SVD-MPE, while in Section 6, we show that this method is a Krylov subspace method when applied to vector sequences that result from the solution of linear systems via fixed-point iterative schemes. Finally, in Section 7, we illustrate its use with two numerical examples.

Before closing, we state the (reduced version of) the well known singular value decomposition (SVD) theorem. For different proofs, we refer the reader to Golub and Van Loan [29] , Horn and Johnson [30] , Stoer and Bulirsch [31] , and Trefethen and Bau [32] , for example.

Theorem 1.1 Let,. Then there exist unitary matrices, , and a diagonal matrix, with, such that

Furthermore, if and, then

In case, there holds, and the rest of the are zero.

Remark: The are called the singular values of and the and are called the corresponding right and left singular vectors of, respectively. We also have

2. Development of SVD-MPE

In what follows, we use boldface lower case letters for vectors and boldface upper case letters for matrices. In addition, we will be working with general inner products and the norms induced by them: These are defined as follows:

・ In, with hermitian positive definite,

(2.1)

・ In, with hermitian positive definite,

(2.2)

Of course, the standard Euclidean inner product and the norm induced by it are obtained by letting in (2.1) and in (2.2); we will denote these norms by (we will denote by the identity matrix in every dimension).

2.1. Summary of MPE

We begin with a brief summary of minimal polynomial extrapolation (MPE). We use the ideas that follow to develop our new method.

Given the vector sequence in, we define

(2.3)

and, for some fixed n, define the matrices via

(2.4)

Clearly, there is an integer, such that the matrices, , are of full rank, but is not; that is,

(2.5)

(Of course, this is the same as saying that is a linearly independent set, but is not.) Following this, we pick a positive integer and let the vector be the solution to

(2.6)

This minimization problem can also be expressed as in

(2.7)

and, as is easily seen, is the standard least-squares solution to the linear system, which, when, is overdetermined, and generally inconsistent. With determined, set, and compute the scalars via

(2.8)

provided. Note that

(2.9)

Finally, set

(2.10)

as the approximation to, whether is the limit or antilimit of.

What we have so far is only the definition (or the theoretical development) of MPE as a method. It should not be taken as an efficient computational procedure (algorithm), however. For this topic, see [14] , where numerically stable and computationally and storagewise economical algorithms for MPE and RRE are designed for the case in which. A well documented FORTRAN 77 code for implementing MPE and RRE in a unified manner is also provided in [14] , Appendix B.

2.2. Development of SVD-MPE

We start by observing that the unconstrained minimization problem for MPE given in (2.7) can also be expressed as a superficially “constrained” minimization problem as in

(2.11)

For the SVD-MPE method, we replace this “constrained” minimization problem by the following actual constrained minimization problem:

(2.12)

With determined, we again compute via

(2.13)

provided, noting again that

(2.14)

Finally, we set

(2.15)

as the SVD-MPE approximation to, whether is the limit or antilimit of.

Of course, the minimization problem in (2.12) has a solution for. Let for this (optimal). Lemma 2.1 that follows next gives a complete characterization of and the (optimal).

Lemma 2.1 Let be the singular values of the matrix

(2.16)

ordered as in

(2.17)

and let be the corresponding right singular vectors of, that is,

(2.18)

Assuming that, the smallest singular value of, is simple, the (optimal) solution to the minimi- zation problem in (2.12) is unique (up to a multiplicative constant,), and is given as in

(2.19)

Proof. The proof is achieved by observing that, with,

(2.20)

so that the problem in (2.12) becomes

(2.21)

The (optimal) solution to this problem is and. We leave the details to the reader. □

In view of the nature of the solution for the (optimal) involving singular values and vectors, as described in Lemma 2.1, we call this new method SVD-MPE.

Remarks:

1) Recall that there exists a positive integer, such that, for, but

. Therefore, we have for all.

2) Of course, exists if and only if the (optimal) satisfies. In addition, by (2.13), the are unique when is simple.

Before we go on to the development of our algorithm in the next section, we state the following result concerning the finite termination property of SVD-MPE, whose proof is very similar to that pertaining to MPE and RRE given in [13] :

Theorem 2.2 Let be the solution to the nonsingular linear system, and let be the se- quence obtained via the fixed-point iterative scheme, with chosen arbitrarily. If k is the degree of the minimal polynomial of with respect to (equivalently, with respect to)2, then produced by SVD-MPE satisfies.

3. Error Estimation

We now turn to the problem of estimating at zero cost the error, whether is the limit or antilimit of. Here we assume that is the solution to the system of equations

and that the vector sequence is obtained via the fixed-point iterative scheme

being the initial approximation to the solution.

Now, if is some approximation to, then a good measure of the error in is the residual vector of, namely,

This is justified since. We consider two cases:

1) is linear; that is, , where and is nonsingular.

In this case, we have

and, therefore, by, satisfies

and thus

(3.1)

2) is nonlinear.

In this case, assuming that and expanding about, we have

where is the Jacobian matrix of the vector-valued function evaluated at. Recalling that, we rewrite this in the form

from which, we conclude that the vectors and satisfy the approximate equality

That is, for all large m, the sequence behaves as if it were being generated by an N-dimensional approximate linear system of the form through

where and In view of what we already know about for linear systems [from (3.1)], for nonlinear systems, close to convergence, we have

(3.2)

Remark: That the vector is the exact residual vector for from linear systems and a true app- roximate residual vector for from nonlinear systems was proved originally in Sidi [14] . was adopted in a subsequent paper by Jbilou and Sadok [15] and named the “generalized residual.” Despite sounding interesting, this name has no meaning and is also misleading. By expanding about the solution and retaining first order terms only, it can be shown that is actually a genuine approximation to the true residual vector when is nonlinear. There is nothing “generalized” about it.

Now, we can compute at no cost in terms of the quantities that result from our algorithm, without having to actually compute itself. Indeed, we have the following result on, which can be incor- porated in the algorithm for SVD-MPE that we discuss in the next section:

Theorem 3.1 Let be the smallest singular value of and let be the corresponding right singular vector. Then the vector resulting from satisfies

(3.3)

Proof. First, the solution to (2.12) is by (2.19). Next, letting, we have by (2.13). Consequently,

Thus, by Lemma 2.1, we have

which is the required result. □

4. Algorithm for SVD-MPE

We now turn to the design of a good algorithm for constructing numerically the approximation that results from SVD-MPE. We note that matrix computations in floating-point arithmetic must be done with care, and this is what we would like to achieve here.

In this section, we let and for simplicity. Thus,. Since there is no room for confu- sion, we will also use, , and to denote, , and, respectively.

As we have seen in Section 2, to determine, we need, the right singular vector of corresponding to its smallest singular value. Now, and can be obtained from the singular value decomposition (SVD) of. Of course, the SVD of can be computed by applying directly to the algori- thm of Golub and Kahan [34] , for example. Here we choose to apply SVD to in an indirect way, which will result in a very efficient algorithm for SVD-MPE that is economical both computationally and storagewise in an optimal way. Here are the details of the computation of the SVD of, assuming that:

1) We first compute the QR factorization of in the form

(4.1)

where is unitary (that is,) and is upper triangular with positive diagonal elements, that is,

(4.2)

(4.3)

Of course, we can carry out the QR factorizations in different ways. Here we do this by the modified Gram- Schmidt process (MGS) in a numerically stable way as follows:

1. Compute and.

2. For do

Set

For do

and

end do (i)

Compute and.

end do (j)

Note that the matrices and are obtained from and, respectively, as follows:

(4.4)

For MGS, see [29] , for example.

2) We next compute the SVD of: By Theorem 1.1, there exist unitary matrices,

(4.5)

and a square diagonal matrix,

(4.6)

such that

(4.7)

In addition, since is nonsingular by our assumption that, we have that for all i. Consequently,.

3) Substituting (4.7) in (4.1), we obtain the following true singular value decomposition of:

(4.8)

Thus, , the singular values of, are also the singular values of, and, the corresponding right singular vectors of, are also the corresponding right singular vectors of. (Of course, the are corres- ponding left singular vectors of. Note that, unlike, , and, which we must compute for our alg- orithm, we do not need to actually compute because we do not need in our computations. The mere knowledge that the SVD of is as given in (4.8) suffices to conclude that is the required optimal solution to (2.12); we continue with the development of our algorithm from this point.)

Remark: Computing the SVD of a matrix by first forming its QR factorization, next com- puting the SVD of as, and finally setting, with was first suggested by Chan [35] .

With already determined, we next compute the as in (2.13); that is,

(4.9)

provided.

Next, by the fact that

and by (2.14), we can re-express in (2.15) in the form

(4.10)

where the are computed from the as in

(4.11)

Making use of the fact that, with

(4.12)

where the and the are exactly those that feature in (4.2) and (4.3), we next rewrite (4.10) as in

(4.13)

Thus, the computation of can be carried out economically as in

(4.14)

Of course, is best computed as a linear combination of the columns of, hence (4.14) is computed as in

(4.15)

It is clear that, for the computation in (4.14) and (4.15), we need to save both and.

This completes the design of our algorithm for implementing SVD-MPE. For convenience, we provide a systematic description of this algorithm in Table 1, where we also include the computation of the norm of

the exact or approximate residual vector, namely, , which is given in Theorem 3.1.

Note that the input vectors, need not be saved; actually, they are overwritten by, as the latter are being computed. As is clear from the description of MGS given above, we can overwrite the matrix simultaneously with the computation of and, the vector overwriting as soon as it is computed, that is, at any stage of the QR factorization, we store N-dimensional vectors in the memory. Since in our applications, the storage requirement of the matrix is negligible. So is the cost of computing the SVD of, and so is the cost of computing the -dimensional vector. Thus, for all practical purposes, the computational and storage requirements of SVD-MPE are the same as those of MPE.

Remark: If we were to compute the SVD of, namely, , directly- and not by 1) first carrying out the QR factorization of as, and 2) next computing the SVD of as, and 3) noting that without actually computing―then we would need to waste extra resources in carrying out the computation of This direct strategy will have either of the following consequences:

1) If we have storage limitations, then we would have to overwrite with. (Recall that both of these matrices are and hence they are large.) As a result, we would have to compute the, a second time in order to compute.

2) If we do not want to compute the vectors, a second time, then we would have to save, while computing the matrix in its singular value decomposition. Thus, we would need to save two matrices, namely, and in the core memory simultaneously. Clearly, this limits the size of k, the order of extrapolation hence the rate of acceleration, severely.

Clearly, the indirect approach we have taken here for carrying out the singular value decomposition of

enables us to save extra computing and storage very conveniently when N is very large.

5. Determinant Representations for SVD-MPE

In [7] and [16] , determinant representations were derived for the vectors that are produced by the vector extrapolation methods MPE, RRE, MMPE, and TEA. These representations have turned out to be very useful in the analysis of the algebraic and analytic properties of these methods. In particular, they were used for obtaining interesting recursion relations among the and in proving sharp convergence and stability theorems for them. We now derive two analogous determinant representations for produced by SVD-MPE.

The following lemma, whose proof can be found in [7] , Section 3, will be used in this derivation in Theorem 5.2.

Lemma 5.1 Let and be scalars and let the satisfy the linear system

(5.1)

Then, whether are scalars or vectors, there holds

(5.2)

where

(5.3)

provided. In case the are vectors, the determinant is defined via its ex- pansion with respect to its first row.

For convenience of notation, we will write

Then is the principal submatrix of obtained by deleting the last row and the last column of. In addition, is hermitian positive definite just like.

Theorem 5.2 that follows gives our first determinant representation for resulting from SVD-MPE and is based only on the smallest singular value of and the corresponding right singular vector.

Theorem 5.2 Define

(5.4)

and assume that

³ (5.5)

Then, provided, exists and has the determinant representation

(5.6)

where is the determinant defined as in (5.3) in Lemma 5.1 with the as in (5.4).

Proof. With as in (2.16), we start by rewriting (2.18) in the form

(5.7)

Invoking here, which follows from (2.19), and multiplying the resulting equality on the left by, we obtain

(5.8)

Dividing both sides of this equality by, and invoking (2.13), we have

(5.9)

which, by the fact that

is the same as

(5.10)

where we have invoked (5.4). We will be able to apply Lemma 5.1 to prove the validity of (5.6) if we show that, in (5.10), the equations with are linearly independent, or, equivalently, the first k rows of the matrix

are linearly independent. By the fact that

we have

where

and

Invoking, we obtain

Since is the smallest eigenvalue of and since, it turns out that is positive definite, which guarantees that the first k rows of are linearly independent. This completes the proof. □

Remark: We note that the condition that in Theorem 5.2 is equivalent to the condition that

, which we have already met in Section 2.

The determinant representation given in Theorem 5.3 that follows is based on the complete singular value decomposition of, hence is different from that given in Theorem 5.2. Since there is no room for confusion, we will denote the singular values and right and left singular vectors and of by, and respectively.

Theorem 5.3 Let be as in (2.16), and let

be the singular value decomposition of; that is,

and

Define

(5.11)

Then, has the determinant representation

(5.12)

where is the determinant defined as in (5.3) in Lemma 5.1 with the as in (5.11).

Proof. By Theorem 1.1,

(5.13)

Therefore,

(5.14)

By (2.16) and by the fact that, which follows from (2.19), and by the fact that, , which follows from (2.13), and by (5.14), we then have

(5.15)

But, by (5.11), (5.15) is the same as

Therefore, Lemma 5.1 applies with as in (5.11), and the result follows. □

6. SVD-MPE as a Krylov Subspace Method

In Sidi [17] , we discussed the connection of the extrapolation methods MPE, RRE, and TEA with Krylov subspace methods for linear systems. We now want to extend the treatment of [17] to SVD-MPE. Here we recall that a Krylov subspace method is also a projection method and that a projection method is defined uniquely by its right and left subspaces4. In the next theorem, we show that SVD-MPE is a bona fide Krylov subspace method and we identify its right and left subspaces.

Since there is no room for confusion, we will use the notation of Theorem 5.3.

Theorem 6.1 Let be the unique solution to the linear system which we express in the form

and let the vector sequence be produced by the fixed-point iterative scheme

Define the residual vector of via Let also be the approximation to prod- uced by SVD-MPE. Then the following are true:

1) is of the form

(6.1)

2) The residual vector of, namely, , is orthogonal to the subspace

Thus,

(6.2)

Consequently, SVD-MPE is a Krylov subspace method for the linear system, with the Krylov subspace as its right subspace and

as its left subspace.

Proof. With the generated as above, we have

Therefore,

and

Upon substituting in this equality, we obtain (6.1).

To prove (6.2), we first recall that by (3.1). By this and by (5.15), the result in (6.2) follows. □

Remark: We recall that (see [17] ), when applied to linearly generated sequences as in Theorem 6.1, MPE, RRE, and TEA are mathematically equivalent to, respectively, the full orthogonalization method (FOM) of Arnoldi [36] , the generalized minimum residual method (GMR), the best implementation of it being GMRES by Saad and Schultz [37] , and the method of Lanczos [38] . In all these methods the right subspace is the k-dimensional Krylov subspace. The left subspaces are also Krylov subspaces, with 1) for FOM, 2) for GMR, and 3) for the method of Lanczos. One important point about the left subspaces of these three methods is that they expand as k increases, that is, the left subspace of dimension contains the left subspace of dimension k. As for SVD-MPE, its right subspace is also the k-dimensional Krylov subspace, which makes SVD-MPE a bona fide Krylov subspace method, and the left subspace is. Thus, the k-dimensional left subspace is not a Krylov subspace, since it is not contained in the left subspace of dimension, as the left singular vectors of are different from the left singular vectors of.

7. Numerical Examples

We now provide two examples that show the performance of SVD-MPE and compare SVD-MPE with MPE. In both examples, SVD-MPE and MPE are implemented with the standard Euclidean inner product and the norm induced by it. Thus, and throughout.

As we have already mentioned, a major application area of vector extrapolation methods is that of numerical solution of large systems of linear or nonlinear equations by fixed-point iterations. [Here is a possibly preconditioned form of.] For SVD-MPE, as well as all other poly- nomial methods discussed in the literature, the computation of the approximation to, the solution of, requires of the vectors to be stored in the computer memory. For systems of very large dimension N, this means that we should keep k at a moderate size. In view of this limitation, a practical strategy for systems of equations is cycling, for which n and k are fixed. Here are the steps of cycling:

C0) Choose integers, and and an initial vector.

C1) Compute the vectors [via].

C2) Apply SVD-MPE (or MPE) to the vectors, with end result.

C3) If satisfies accuracy test, stop.

Otherwise, set, and go to Step C1.

We will call each application of steps C1 - C3 a cycle, and denote by the that is computed in the rth cycle. We will also denote the initial vector in step C0 by. Numerical examples suggest that the se-

quence has very good convergence properties. (A detailed study of errors and convergence properties for MPE and RRE in the cycling mode is given in [20] and [21] .)

Note that the remark at the end of Section 4 is relevant to the implementation of SVD-MPE in the cycling mode when N, the dimension of the, is very large and storage is limited and, therefore, the size of k is limited as well.

Example 7.1 Consider the vector sequence obtained from, where

and is symmetric with respect to both main diagonals, and and is hermitian. Therefore, is diago- nalizable with real eigenvalues. The vector is such that the exact solution to is. We have, so that converges to.

Figure 1 shows the norms of the errors in, with fixed. Here. Note that all of the approximations make use of the same (infinite) vector sequence, and, practically speaking, we are looking at how the methods behave as. It is interesting to see that SVD-MPE and MPE behave almost the same. Although we have a rigorous asymptotic theory confirming the behavior of MPE in this mode as observed in Figure 1 (see [16] [18] and [19] ), we do not have any such theory for SVD-MPE at the present5.

Figure 2 shows the norm of the error in in the cycling mode with and. Now, a relatively large dimension.

Example 7.2 We now apply SVD-MPE and MPE to the nonlinear system that arises from finite-difference approximation of the two-dimensional convection-diffusion equation considered in Kelley ( [39] , pp. 108-109), namely,

where satisfies homogeneous boundary conditions. is constructed by setting in the differential equation and by taking

as the exact solution.

The equation is discretized on a square grid by approximating, , , and by centered differe- nces with truncation errors. Thus, letting, and

and

and

we replace the differential equation by the finite difference equations

with

Here is the approximation to, as usual.

We first write the finite difference equations in a way that is analogous to the PDE written in the form

and split the matrix representing to enable the use of the Jacobi and Gauss-Seidel methods as the iterative procedures to generate the sequences.

Figure 3 and Figure 4 show the norms of the errors in from SVD-MPE and MPE in the cycling mode with and, the iterative procedures being, respectively, that of Jacobi and that of Gauss- Seidel for the linear part of the PDE. Here, so that the number of unknowns (the dimension) is. Note that the convergence of cycling is much faster with Gauss-Seidel iteration than with

Jacobi iteration6. For both cycling computations, SVD-MPE and MPE seem to perform very similarly in this example.

Note that the Jacobi and Gauss-Seidel iterations converge extremely slowly. In view of this slow conve- rgence, the acceleration produced by SVD-MPE and MPE in the cycling mode is remarkable.

Acknowledgements

The author would like to thank Boaz Ophir for carrying out the computations reported in Section 7 of this work.

Cite this paper

Avram Sidi, (2016) SVD-MPE: An SVD-Based Vector Extrapolation Method of Polynomial Type. Applied Mathematics,07,1260-1278. doi: 10.4236/am.2016.711111

References