Applied Mathematics
Vol.07 No.10(2016), Article ID:67403,6 pages
10.4236/am.2016.710094
Transformation of the Navier-Stokes Equation to the Cauchy Momentum Equation Using a Novel Mathematical Notation
Robert Goraj
Paul Gossen Str. 99, 91052 Erlangen, Germany

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 15 April 2016; accepted 13 June 2016; published 16 June 2016
ABSTRACT
A transformation way of the Navier-Stokes differential equation was presented. The obtained re- sult is the Cauchy momentum equation. The transformation was performed using a novel shorten mathematical notation presented at the beginning of the transformation.
Keywords:
Navier-Stockes Equation, Cauchy Momentum Equation, Mathematical Notations

1. Introduction
In order to write mathematical equations and formulas one needs a certain mathematical notation. The mathe- matical notation includes letters from Roman, Greek, Hebrew and German alphabets as well as Hindu-Arabic numerals. The origin of our present system of numerical notation is ancient, by it was in use among the Hindus over two thousand years ago. Addition was indicated by placing the numbers side by side and subtraction by placing a dot over the number to be subtracted. The division was similar to our notation of fractions (the divisor placed below the dividend) by without the use of bar.
The Swiss mathematician Leonard Euler contributed the use of the letter e to represent the base of natural logarithms, the letter π which is used among others to give the perimeter of a circle and the letter i to represent the square root of negative one. He introduces also the symbol ∑ for summations and the letter Γ for the gamma- function. Euler was the first one who used the notation f(x) to represent the function of the variable x. The English mathematician William Emerson [1] developed the proportionality sign: ∝.
The German mathematician Gottfried Wilhelm Leibniz used the letter d to indicate the differentiation. He in-
troduced the notation, which represents derivatives as if they were a special type of fraction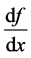 . This notation
. This notation
makes explicit the variable with respect to which the derivative of the function is taken. The Italian mathematician Joseph-Louis Lagrange introduces the prime symbol to indicate derivatives. The English physicist and mathematician Isaac Newton used a dot placed above the function e.g.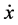 , which is still in use for denoting derivatives of physical quantities with respect to time. The French philosopher and mathematician Nicolas de Condorcet introduced the sign ∂ for partial differentials. The Irish physicist and mathematician William Rowan Hamilton introduced the nabla symbol ∇ for vector differentials. The name nabla comes after the musical instrument, the harp, which is the symbol shape-similar to. The French mathematician Pierre-Simon Laplace developed and widely used Laplacian differentiation operator ∆.
, which is still in use for denoting derivatives of physical quantities with respect to time. The French philosopher and mathematician Nicolas de Condorcet introduced the sign ∂ for partial differentials. The Irish physicist and mathematician William Rowan Hamilton introduced the nabla symbol ∇ for vector differentials. The name nabla comes after the musical instrument, the harp, which is the symbol shape-similar to. The French mathematician Pierre-Simon Laplace developed and widely used Laplacian differentiation operator ∆.
One of the most famous notations is the Einstein notation also known as the Einstein summation convention. According to this notation the summation symbol ∑ is omitted and replaced by indexing of coordinates [2] - [4] . One of the applications of this notation is the relativistic mechanics, in which one normally deals with covariant and contravariant vectors or tensors. For example the covariant metric tensor defined as:
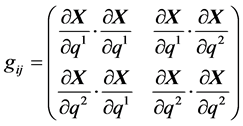
can be shortened using the Einstein notation to:
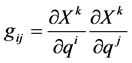
where k is the summation index, X the position vector and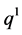 ,
, 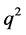 are the components of the vector q.
are the components of the vector q.
2. Definition of the Shorten Mathematical Notation
In order to minimise the length of mathematic equations presented in the article the following shorten mathematical notation according to [5] has been used:
Ø Scalar variables are indicated using the cursive writing
Ø Vector variables are indicated using the straight writing
Ø Derivatives are indicated using the down index of the state variable. The state variables are the following 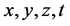
Ø In the case of partial derivatives the cursive writing of a state variable is used
Ø In the case of the total derivative in time the straight writing “t” is used
Ø Components of a vector are indicates using the upper index
A few examples of the shorten notation was showed in the Table 1.
Table 1 has an objective to demonstrate that both the length and the height of the presented expressions can be shortened if using the indexing for the differentiation instead of the the letter d and the bar.
3. Derivation
For the Navier-Stokes momentum differential equation of the compressible fluid and constant viscosity over the fluid in the convective form yields [6] :
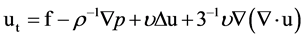 (1)
(1)
For the left side of (1) can be written [7] :
 (2)
(2)
Multiplying (2) by 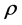 and making use of the continuity equation [8] :
and making use of the continuity equation [8] :
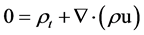 (3)
(3)
Table 1. Examples of notations of mathematical equations [5] .
yields:
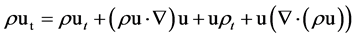 (4)
(4)
The components of u are defined in Cartesian co-ordinate system as follows: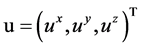 . The first and the third term of the right side of (4) can be put together to:
. The first and the third term of the right side of (4) can be put together to:
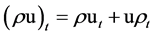 (5)
(5)
Making use of the relation [9] :

where the symbol 

one can express the sum of the second and fourth term of (4) as follows:

For the sum of (5) and (8) yields:

The product 

For the last and the last but one term of the right side of (1) divided by 



The vector w in (11) to (13) is the auxiliary quantity, which total derivative in time equals:

After some modifications the Equations (11) to (13) become:



The Equations (15) to (17) can be expressed as the divergence of the following vectors:



The vectors in brackets can now be used for building of the tensor:

where:

The tensor (21) can also be written using outer product and unit matrix as follows:

The use of (9), (10) and (23) in (1) yields:

The Equation (24) is the Cauchy momentum equation [6] .
4. Conclusions, Novelties and Meaning of the Work
In the applied mathematics researchers use different notations for vectors indicating physical quantities. They frequently use capital letters and the bold type writing both strait or italic (e. g. to indicate the magnetic flux density B or B). In some works one can see a very academic way of writing vectors using an arrow above the vector. The differentiation is based on the letter d or the sign ∂ and the use of bar as if differentiation would be a type of fraction. In order to shorten both the length and the height of the presented expressions and in the same time do them easier to read, one can apply the presented novel notation, which bases on indexing of functions. The presented derivation of the Cauchy momentum Equation (24) shows how big is the reduction of the room needed for the writing of the used equations. As a comparison example one can write the Equations (15) to (17) in a conventional way:



And then tries to express them according to (18) - (20) as the divergence of vectors:



One can recognize that e. g. the symbol 

Cite this paper
Robert Goraj, (2016) Transformation of the Navier-Stokes Equation to the Cauchy Momentum Equation Using a Novel Mathematical Notation. Applied Mathematics,07,1068-1073. doi: 10.4236/am.2016.710094
References
- 1. Emerson, W. (1794) The Elements of Geometry. Library of the University of Michigan, London.
- 2. Epstein, M. (2014) Differential Geometry, Basic Notions and Physical Examples. International Publishing, Springer, Cham, Heidelberg, New York, Dordrecht, London.
- 3. McInerney, A. (2013) First Steps in Differential Geometry, Riemannian, Contact, Symplectic. Springer, New York.
http://dx.doi.org/10.1007/978-1-4614-7732-7 - 4. Nguyen-Schafer, H. and Schmidt, J.-P. (2014) Tensor Analysis and Elementary Differential Geometry for Physicists and Engineers. Springer, Berlin Heidelberg.
- 5. Goraj, R. (2015) Impact of the Pulse Width Modulation on the Temperature Distribution in the Armature of the Solenoid Valve. International Journal of Applied Mechanics and Engineering, 20, 773-786.
http://dx.doi.org/10.1515/ijame-2015-0050 - 6. Batchelor, G.K. (1967) An Introduction to Fluid Dynamics. Cambridge University Press, Cambridge.
- 7. Puzyrewski, R. and Sawicki, J. (2000) Fundamentals of Fluid Mechanics and Hydraulics. Wydawnictwo Naukowe PWN, Warszawa.
- 8. Grybos, R. (2002) A Collection of Tasks with the Fluid Mechanics. Wydawnictwo Naukowe PWN, Warszawa.
- 9. Bronstein, I.N., Semendjajew, K.A., Musiol, G. and Mühlig, H. (2000) Handbook of Mathematics. Edition Harri Deutsch, Berlin.
- 10. Goraj, R. (2016) Re-Derivation of Laplace Operator on Curvilinear Coordinates Used for the Computation of Force Acting in Solenoid Valves. Journal of Applied Mathematics and Computational Mechanics, 15, 25-38.
http://dx.doi.org/10.17512/jamcm.2016.1.03
Physical Quantities Used in the Derivation


