Received 25 December 2015; accepted 26 February 2016; published 29 February 2016

ABSTRACT

We study the periodic solutions of the second-order differential equations of the form

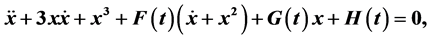
where the functions, 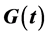and 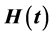are periodic of period 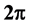in the variable t.

Keywords:

Periodic Solution, Differential Equation, Averaging Theory

1. Introduction and Statement of the Main Results

In this paper we shall study the existence of periodic solutions of the second-order differential equation of the form

(1)

where the dot denotes derivative with respect to the time t, and the functions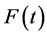, 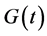and 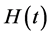are periodic of period 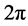in the variable t.

We note that the second-order differential Equation (1), when, appears in the Ince’s catalog of equations possessing the Painlevé property (see [1] ). Moreover, the differential equation 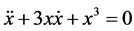is well known in many areas of mathematics and physics, and it possesses the algebra 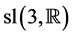of Lie point symmetries (see for more details in the paper [2] and the references quoted there).

In a recent paper [3] (see also [4] [5] ), the second-order differential Equation (1) has been studied when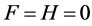. A study of coupled quadratic unharmonic oscillators in terms of the Painlevé analysis and inte- grability can be seen in [6] , and studies on the second-order differential equations can be seen in [7] . Other approach to the periodic solutions of second-order differential equations can be found in [8] .

Here we study the periodic solutions of the second-order differential Equation (1) when, , and with. Our main results are the following ones.

Theorem 1. We define the functions

(2)

where

Assume that the functions, and are -periodic. Then for sufficiently small and for every solution of the system for, satisfy

(3)

the differential Equation (1) has a -periodic solution.

Theorem 1 is proved in section 3 using the averaging theory described in section 2. Two applications of Theorem 1 are the following.

Corollary 1. We consider the differential Equation (1) with, and. Then for sufficiently small, this differential equation has a -periodic solution.

Corollary 2. We consider the differential Equation (1) with, and. Then for sufficiently small, this differential equation has a -periodic solution.

Corollaries 1 and 2 are also proved in section 3.

Theorem 2. Assuming that

and setting

(4)

with

Assume that, and are -periodic functions. Then for sufficiently small and for every solution of the system for satisfy (3), the differential Equation (1) has a periodic solution

Theorem 2 is proved in section 4. Two applications of Theorem 2 are the following.

Corollary 3. We consider the differential Equation (1) with, and. Then for sufficiently small, this differential equation has a -periodic solution

Corollary 4. We consider the differential Equation (1) with, and . Then for sufficiently small, this differential equation has a periodic solution

Corollaries 3 and 4 are also proved in section 4.

2. Basic Results on Averaging Theory

We state the results from the averaging method that we shall use for proving the results of this work.

We consider differential systems of the form

(5)

where is a small parameter, and the functions and are functions, T-periodic in the variable t, and is an open subset of. Suppose that the unperturbed system

(6)

has a submanifold of dimension n of T-periodic solutions, i.e. of periodic solutions of period T.

We denote by the solution of system (6) such that. We consider the first variational equation of system (6) on the periodic solution, i.e.

(7)

where is an matrix. Let the fundamental matrix of system (7) such that is the identity matrix of.

By assumption there exists an open set V such that and for each, is T-periodic. Therefore we have the following result.

Theorem 3. We suppose that there is an open and bounded set V with such that for each, the solution is T-periodic, and let be the function defined by

(8)

If there is with and, then there is a T-periodic solution of system (5) satisfying.

Theorem 3 is due to Malkin [9] and Roseau [10] , for a new and shorter proof (see [11] ).

3. Proof of Theorem 1 and Its Two Corollaries

Proof of Theorem 1. Introducing the variable, we can write the second-order differential Equation (1) as the following first-order differential system

(9)

Doing the rescaling, we obtain the system

(10)

System (10) with is the unperturbed system, otherwise system (10) is the perturbed system. The unperturbed system has a unique singular point, the origin of coordinates. The solution of the unperturbed system such that is

Note that all these periodic orbits have period. Using the notation introduced in section 2. We have that, , , and .

The fundamental matrix solution is independent of the initial condition, and denoting it by we obtain

Now we compute the function given in (8), and we get the functions (2) of the statement of Theorem 1.

By Theorem 3 each zero of system satisfying (3), provides a - periodic solution of system (10) with sufficiently small such that

Going back through the change of variables for every periodic solution of system (10) with sufficiently small, we obtain a -periodic solution of the differential Equation (1) with sufficiently small. This completes the proof of Theorem 1. □

Proof of Corollary 1. We must apply Theorem 1 with

We compute the functions and of the statement of Theorem 1, and we obtain

System has the zero. Since the Jacobian (3) at this zero is, we obtain using Theorem 1 the periodic solution given in the statement of the corollary. □

Proof of Corollary 2. We apply Theorem 1 with

Computing the functions and of Theorem 1 we get

System has the zero. Since the Jacobian (3) at this zero is the corollary follows. □

4. Proof of Theorem 2 and Its Corollaries

Proof of Theorem 2. As in the proof of Theorem 1, the second-order differential Equation (1) can be written as the first order differential system (9). Doing the rescaling, we obtain the system

(11)

System (11) with is the unperturbed system, otherwise it is the perturbed system.

The solution of the unperturbed system such that is

Note that these periodic orbits have period. Using the notation introduced in section 2. We have that, , , and .

The fundamental matrix solution is independent of the initial condition and it is

We compute the function given in (8), and we get the functions (4) of the statement of Theorem 2.

By Theorem 3, each zero of system satisfying (3), provides a - periodic solution of system (11) with sufficiently small such that

Going back through the change of variables for every periodic solution of system (11) with sufficiently small, we obtain a -periodic solution

of the differential Equation (1) for sufficiently small. This completes the proof of Theorem 2. □

Proof of Corollary 3. We apply Theorem 2 with

We compute the functions and of the statement of Theorem 2, and we obtain

System has the solution. Since the Jacobian (3) is, by Theorem 2 we obtain the periodic solution of the statement of the corollary. □

Proof of Corollaryc 4. We apply Theorem 2 with

We compute the functions and of the statement of Theorem 2, and we obtain

System has the solution. Since the Jacobian (3) is, by Theorem 2 we obtain the periodic solution of the statement of the corollary. □

Acknowledgements

The second author is partially supported by a MINECO grant MTM2013-40998-P, an AGAUR grant number 2014SGR568, and the grants FP7-PEOPLE-2012-IRSES 318999 and 316338.

Cite this paper

ZeynebBouderbala,JaumeLlibre,AmarMakhlouf, (2016) Periodic Solutions of a Class of Second-Order Differential Equation. Applied Mathematics,07,227-232. doi: 10.4236/am.2016.73021

References