Received 5 December 2015; accepted 22 January 2016; published 25 January 2016

ABSTRACT

This paper presents a brief demonstration of Schulz’s first conjecture, which sets the upper and lower limits on the length of the shortest chain of addition. Two methods of the upper limit are demonstrated; the second one is based on the algorithm of one of the most popular methods for obtaining addition chains of a number, known as the binary method.

Keywords:

Addition Chain, Exponentiation, Short Chain, Scholz’s Conjecture, Binary Method

1. Introduction

With the development of the Internet and adding chain applications in the development of cryptography―which permits safe handling of data over the Internet―the theme began with the publication in 1937 of Arnold Scholz’s paper [1] , which defines a minimal addition chain, along with his three famous conjectures. In 1939 [2] , Alfred Brauer gave a strong impetus to this issue, gaining importance in this area. During the last decades of the last century deterministic methods flourished. The most popular were the binary method and the window method [3] -[5] . Heuristic methods began to emerge in the 70s and toward the end of the century, began to dominate in the literature [6] [7] . This is the second paper we write on the theme [8] and in both present simple demonstrations, the third and first conjecture, we use deterministic algorithms. Our intention is to build a framework for the development of intelligent methods for generating addition chains.

2. Basic Definitions

The first conjecture presented by Scholz was: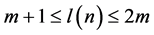; for the n which satisfy:

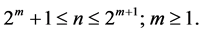(1)

In addition to setting maximum and lower bounds for the minimum length of addition chains, this conjecture induces a partition of our study space, in this case the natural numbers. The bounded sets defined by Schulz 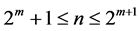for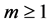, exclude the numbers 1 and 2. For the possible values of n correspond to the set; from there, if we increase m by one, the possible values of n are doubled. The point of this partition is that we can delimit our study space, in this case the natural numbers, to set general properties on addition chains.

We will begin our discussion with the following definitions:

Definition 2.1. Let be a finite sequence of natural numbers. We will call it an addition chain of a natural number if it satisfies:

I..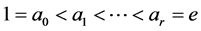

II.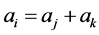, for some 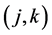and for each step i, , with.

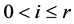Definition 2.2. Let 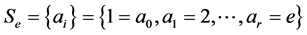be an addition chain of a number e, the highest

index of the sequence r is called length of the chain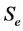, and it is denoted by.

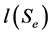Definition 2.3. The minimum length of all addition chains of a natural number e is denoted by, that is:

Definition 2.4. Let us consider the family of natural subsets defined by:

The set will be called ith generation of natural numbers.

Definition 2.5. For every ith generation with, we will define:

even numbers of.

odd numbers of.

Definition 2.6. For every, we will define the nth dominant chain as:

defined by

3. Important Properties

Proposition 3.1. The dominant chains are of maximum growth. That is to say, for every x if with; then.

Proof. As then there exists (since the first two values of any addition chain are the

same) in such a way that as with, as;; because if the first term of the sum had an index less than, at most it could be, which would imply that the sequence would not be an addition chain because it does not strictly increase, and as and the sequence strictly increases we have that:. If it was the last term of the sequence then the inequality is true, and if it was not the last term from there, for at each increment of the difference between the terms of the sequences increases. Hence.

Proposition 3.2. Dominant chains are addition chains defined on the numbers of the form, of length.

Proof. By definition defined by from where:

From the definition of dominant chain:, from where its first element is 1and the last one is, in addition for every i the following is true: from where, therefore it increases and ends in, which proves the first property of addition chain.

Let us have a look at the second property, that is:

clearly, with, so it satisfies the second property and therefore they are addition chains.

Finally, since is an addition chain of, the Proposition (3.1) assures that any other chain of that length is of a number, which implies that it is the only chain of length n de. This proves that.

To underline this last fact we will state the following in this corollary:

Corollary 3.3. The numbers of the form have as minimum length chain, whose length is. This chain is unique.

Proof. The Proposition (3.2) assures that is addition chain of, and the Proposition (3.1) states that any other chain of that length different from makes true, which guarantees the uniqueness of.

Another important result:

Corollary 3.4. If then.

Proof. If implies that there exists in such a way that if by the Proposition (3.1), we have that and if by the Proposition (3.2) we know that from where.

Proposition 3.5. If, then.

Proof. If we assume that (3.5) is not true, then there exists in such a way that; from where if there exists in such a way that. The Corollary (3.4) assures that, and this implies that, which contradicts our hypothesis, from which we conclude that if then.

Proposition 3.6. If, then for any.

Proof. As, then there exists in such a way that. Let be a minimum length chain of x, from this one we will build an addition chain of z.

, it is clearly an addition chain of z, of length, which proves that

.

Proposition 3.7. If and, then and.

Proof. As x is an even number and lower than the upper limit of, that is; then from where, which guarantees that.

Let be a minimum length chain, then its first term is 1 and its last term is x, from where if we add as the last term to that sequence, now this sequence is an addition chain of z, that is:, it is an addition chain of Z of length, from where.

Proposition 3.8. If, then for any.

Proof. By definition, odd numbers, from where:

, from these numbers only the first does not have an even numbered predecessor in, an addition chain of this number is given by, whose length is

, this length is minimum since if there exists another chain of z with a length lower than n according to the Corollary (3.4), we have that and clearly, from where we conclude that it is minimum, that is. For the rest of the elements of, according to the Proposition (3.7), there exists a in such a way that. Now, the Proposition (3.6) assures in

such a way that, from where for any.

Proposition 3.9. For every; is a partition of.

Proof. We have to demonstrate that for every we will always have:

a).

b).

For we have according to the definition of from where and

and, from where we clearly see that a) and b)

are true.

Proposition 3.10. The number 3 only has an addition chain of length equal to 2.

Proof. The only addition chain of the number 3 is:, we will demonstrate that it is an addition chain and that it is unique.

It is an addition chain since it begins with 1, it has increasing terms and it ends with the number 3, from where it satisfies the property I of the definition of the chain addition.

Clearly and, which proves part II of the definition.

We will demonstrate now that it is unique. Let us suppose that it is not, then there exists, which is

chain of the number 3. Let be an addition chain different from, the defini-

tion of chain forces and the property II when, and, the only possible value of i and j is zero, from where. For the possible values of are three, which are presented in Table 1.

The only possible value for is 3, according to the definition of addition chain it would be the last term of the sequence. However, it is equal to, which contradicts the fact that is different from, from where we conclude that it is unique. As.

4. Demonstration of Scholz’s First Conjecture

In terms of the given definitions, Scholz’s first conjecture is equivalent to:

; for the n which satisfy:.

If we make a change of variables we will have:

for the n which satisfy:.

As the conjecture is now:

; for the.

The new formulation would be:

Theorem 4.1. If, then; for every.

Proof. The Proposition (3.5) guarantees the first part of the inequality, that is: if, then.

We will now demonstrate the second part of the inequality.

The Proposition (3.6) guarantees us that if, then, for any. The Proposition (3.8) guarantees us that if, then, for any. The Proposition (3.9) proves that

, from where if is another upper bound of, we have that for every i,

is true, it is the upper bound of, that is; for every.

Let be the upper bound of; then

(2)

As and, its minimum addition chain is, according to the Corollary (3.3) and the 3 according to the Proposition (3.10), from where the upper bound of is 2. This is, and substituting this value of in (2) we will have:

which proves that if, then; for. This demonstrates the second part of the inequality.

An alternative way of deriving the upper bound established in Schulz’s first conjecture is obtainable by using the binary analysis methods for constructing the addition chains [3] . It is expressed in the following algorithm.

5. Binary Method

Input: an integer:

Output: Addition chain

Start:

for i=1 to m

If then:

End

Therefore the length of the obtained chain depends on the length of the binary expression of the number and the quantity of ones that it has, as for each one, without taking into account the first one, is added another number to the output chain; for example see Table 2.

The output chain has the same number of elements that the number of bytes of the expression, in base 2, of the input number e, plus the quantity of ones of the binary expression, minus one, which is at the beginning of the binary expression. In this case: 77 = 1001101, the length of the binary expression is of 7 bytes and the number of ones minus the first one is 3. Hence the length of the output chain is 7 + 3 = 10; U = {1, 2, 4, 8, 9, 18, 19, 38, 76, 77}. Therefore the length of the addition chain is 9. This fact is expressed in the next proposition, as follows:

Proposition 5.1. The length of the addition chain generated by the binary method of a number e is equal to the last sub-index of the binary expression, plus the quantity of ones it has, minus one. That is, where p is the number of ones that the binary expression e has.

Proof: Take; and its binary expression The algorithm starts with a one and eliminates, it is equal to one, and adds it to the addition chain U. For each element from to that is for m elements we have added one more to U. Then has m plus, where p is quantifies the number of e_i’s equal to one. Therefore, according to Definition 2.2 the length of the addition chain is equal to the last sub-index of the chain, in this case. As m is the last sub-index of the binary expression, and p is the number of ones in the expression. Note that we have that . Then from Definition 2.2, we derive that the length of the chain is the last of the sub-indexes, which is.

Q.E.D.

Note that the numbers belonging to the generation G_i, for have has binary expression with length equal to n, minus the superior limit, which has elements with 1 and n with zeros, which corresponds to the superior limit of the generation, as it is observed in the following Table 3.

Note that the upper bound of the generation is given by 2ⁿ; its minimum addition chain is n, because of Proposition 3.2. Then we do not take i into account. The maximum expected length of a chain, belonging to the generation n, is given by the number whose binary expression is equal to n, corresponding to, one less than the superior limit, with binary expression:. The obtained addition chain will have n − 1 components, as the number of ones of the expression is n, where the addition chain is given by Hence, the length of this chain is, which is the longest generated by the method in that generation. Then is proved the following result:

Corollary 5.1. The length of the longest addition chain generated by the binary method in corresponds to that has as length.

Theorem 5.1. The binary method for the generation of addition chains proofs the right hand side of the First Schulz’s Conjecture that is:

If, then; for every.

Proof. If then n has the binary expression, where at least a component is different form is equal to 1, because if all are zeros, it will be the superior limit of. The generation i has elements whose binary expression has two ones, for these elements, according to Proposition 5.1, its generated addition chain is of length equal to i, as we add only another value and the first value of the generated chain has as sub-index. The rest will have longer chains. The longest corresponding to a has length due to the results of corollary.

This fact proofs that all the chains generated with this method are not larger than. Hence, the minimum chain must be smaller or equal to these values. This last result completes the proof.

Cite this paper

JoséM. Sautto,AgustínSantiago,Carlos N.Bouza,VerónicaCampos, (2016) Scholz’s First Conjecture: A Brief Demonstration. Applied Mathematics,07,70-76. doi: 10.4236/am.2016.71006

References