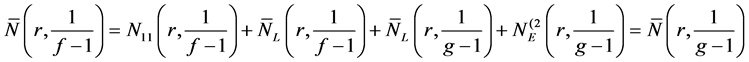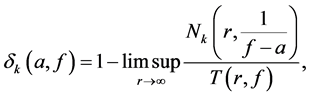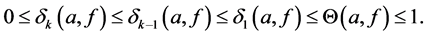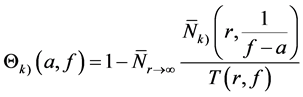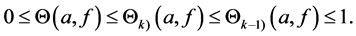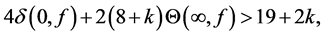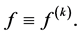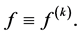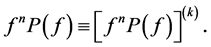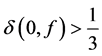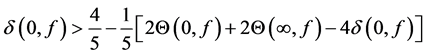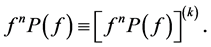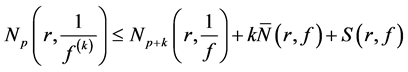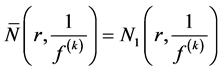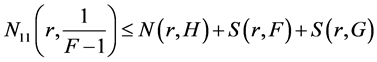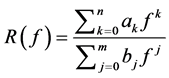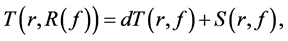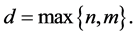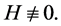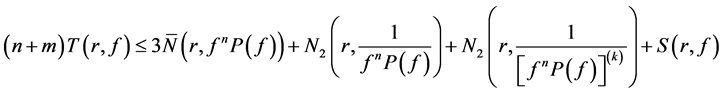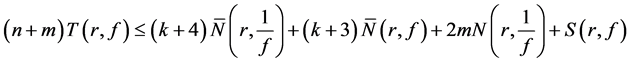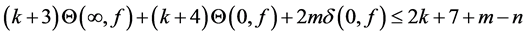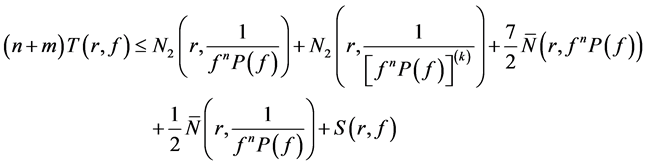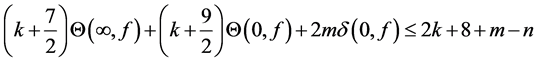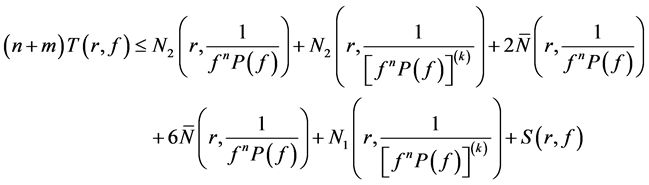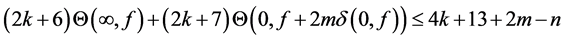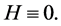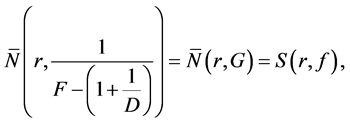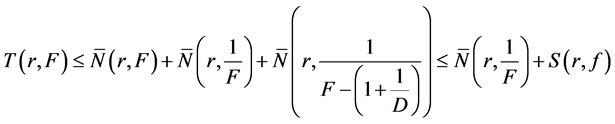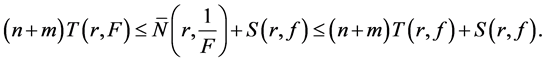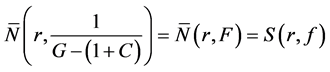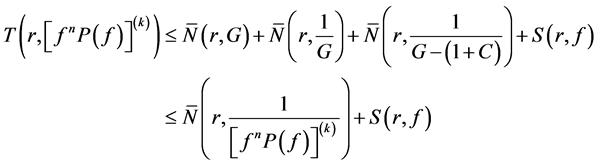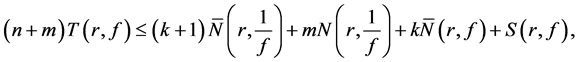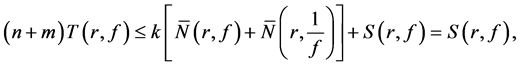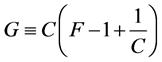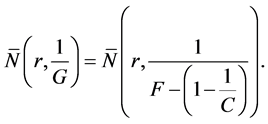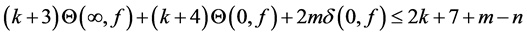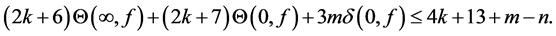Received 19 August 2015; accepted 15 November 2015; published 18 November 2015

ABSTRACT

In this paper, we study the problem of meromorphic functions that share one small function of differential polynomial with their derivatives and prove one theorem. The theorem improves the results of Jin-Dong Li and Guang-Xin Huang [1] .

Keywords:

Uniqueness, Meromorphic Function, Differential Polynomial

1. Introduction and Results

Let denote the complex plane and f be a nonconstant meromorphic function on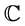. We assume the reader is familiar with the standard notion used in the Nevanlinna value distribution theory such as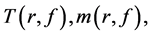 (see, e.g., [2] [3] ), and denotes any quantity that satisfies the condition 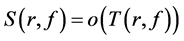as 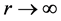outside of a possible exceptional set of finite linear measure. A meromorphic function a is called a small function with respect to f, provided that.

Let f and g be two nonconstant meromorphic functions. Let a be a small function of f and 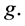We say that f, g share a counting multiplicities (CM) if 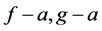have the same zeros with the same multiplicities and we say that f, g share a ignoring multiplicities (IM) if we do not consider the multiplicities. In addition, we say that f

and g share ¥ CM, if 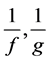share 0 CM, and we say that f and g share ¥ IM, if 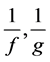share 0 IM. Suppose that f and g share a IM. Throughout this paper, we denote by the reduced counting function of those common a-points of f and g in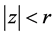, where the multiplicity f each a-point of f is greater than that of the corresponding a-point of g, and denote by the counting function for common simple 1-point of both f and g, and the counting function of those 1-points of f and g where. In the same way, we can define and If f and g share 1 IM, it is easy to see that

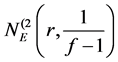
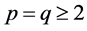
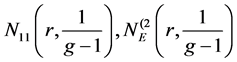
In addition, we need the following definitions:

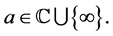
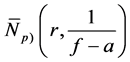
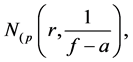
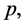
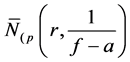
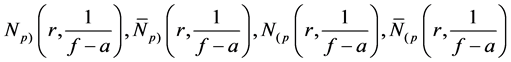
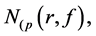
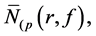
Definition 1.1. Let f be a non-constant meromorphic function, and let p be a positive integer and Then by we denote the counting function of those a-points of f (counted with proper multiplicities) whose multiplicities are not greater that p, by we denote the corresponding reduced counting function (ignoring multiplicities). By we denote the counting function of those a-points of f (counted with proper multiplicities) whose multiplicities are not less than by we denote the corresponding reduced counting function (ignoring multiplicities,) where and what follows, mean respectively, if.

Definition 1.2. Let f be a non-constant meromorphic function, and let a be any value in the extended complex plane, and let k be an arbitrary nonnegative integer. We define

where

Remark 1.1. From the above inequalities, we have

Definition 1.3. Let f be a non-constant meromorphic function, and let a be any value in the extended complex plane, and let k be an arbitrary nonnegative integer. We define

Remark 1.2. From the above inequality, we have

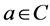
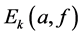
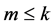
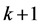
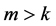
Definition 1.4. (see [4] ). Let k be a nonnegative integer or infinity. For we denote by the set of all a-points of f, where an a-point of multiplicity m is counted m times if and times if. If, we say that f, g share the value a with weight k.

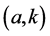
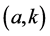
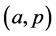
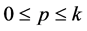
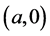
We write f, g share to mean that f, g share the value a with weight k; clearly if f, g share, then f, g share for all integers p with. Also, we note that f, g share a value a IM or CM if and only if they share or, respectively.

R. Bruck [5] first considered the uniqueness problems of an entire function sharing one value with its derivative and proved the following result.

Theorem A. Let f be a non-constant entire function satisfying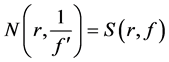. If f and share the value 1 CM, then for some nonzero constant c.

Bruck [5] further posed the following conjecture.

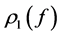
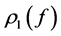
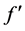
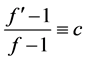
Conjecture 1.1. Let f be a non-constant entire function be the first iterated order of f. If is not a positive integer or infinite, f and share the value 1 CM, then for some nonzero constant.

Yang [6] proved that the conjecture is true if f is an entire function of finite order. Yu [7] considered the problem of an entire or meromorphic function sharing one small function with its derivative and proved the following two theorems.

Theorem B. Let f be a non-constant entire function and be a meromorphic small function. If and share 0 CM and, then.

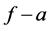
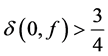
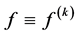
Theorem C. Let f be a non-constant non-entire meromorphic function and 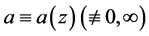be a meromorphic small function. If

1) f and a have no common poles.

2) and share 0 CM.

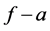
3)

then where k is a positive integer.

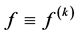
In the same paper, Yu [7] posed the following open questions.

1) Can a CM shared be replaced by an IM share value?

2) Can the condition 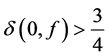of theorem B be further relaxed?

3) Can the condition 3) in theorem C be further relaxed?

4) Can in general the condition 1) of theorem C be dropped?

In 2004, Liu and Gu [8] improved theorem B and obtained the following results.

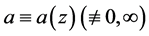
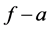
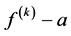
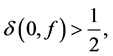
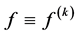
Theorem D. Let f be a non-constant entire function be a meromorphic small function. If and share 0 CM and then.

Lahiri and Sarkar [9] gave some affirmative answers to the first three questions improving some restrictions on the zeros and poles of a. They obtained the following results.

Theorem E. Let f be a non-constant meromorphic function, k be a positive integer, and 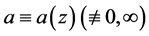be a meromorphic small function. If

1) a has no zero (pole) which is also a zero (pole) of f or 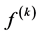with the same multiplicity.

2) and share

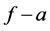
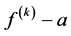
3) then.

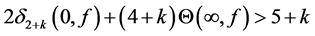
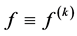
In 2005, Zhang [10] improved the above results and proved the following theorems.

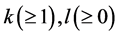
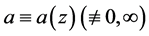
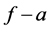
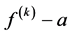
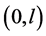
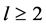
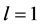
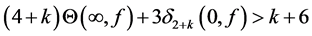
Theorem F. Let f be a non-constant meromorphic function, be integers. Also let be a meromorphic small function. Suppose that and share. If

and

(1)

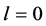
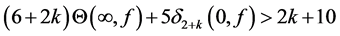
or and

(2)

or and

(3)

then

In 2015, Jin-Dong Li and Guang-Xiu Huang proved the following Theorem.

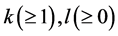
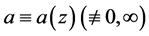
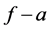
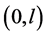
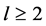
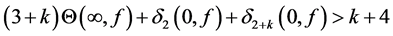
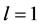
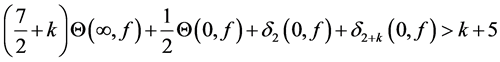
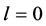
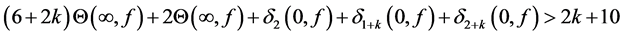
Theorem G. Let f be a non-constant meromorphic function, be integers. Also let be a meromorphic small function. Suppose that and share. If

and

(4)

and

(5)

or and

(6)

then

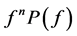
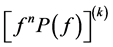
In this paper, we pay our attention to the uniqueness of more generalized form of a function namely and sharing a small function.

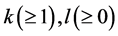
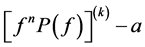
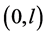
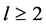
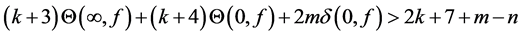
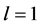
Theorem 1.1. Let f be a non-constant meromorphic function, be integers. Also let be a meromorphic small function. Suppose that and share. If

and

(7)

and

(8)

or and

(9)

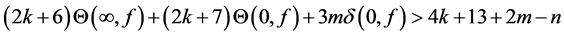
then

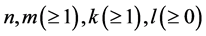
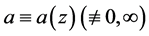
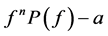
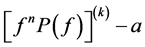
Corollary 1.2. Let f be a non-constant meromorphic function, be integers. Also let

be a meromor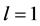phic small function. Suppose that and share. If

and

or 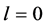and

or and

then

2. Lemmas

Lemma 2.1 (see [1] ). Let f be a non-constant meromorphic function, 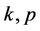be two positive integers, then

clearly

Lemma 2.2 (see [1] ). Let

(10)

where F and G are two non constant meromorphic functions. If F and G share 1 IM and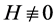, then

Lemma 2.3 (see [11] ). Let f be a non-constant meromorphic function and let

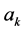
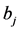
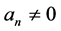
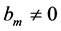
be an irreducible rational function in f with constant coefficients and where and. Then

where

3. Proof of the Theorem

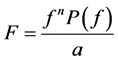
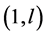
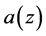
Proof of Theorem 1.1. Let and Then F and G share, except the zeros and poles of. Let H be defined by (10).

Case 1. Let

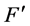
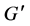
By our assumptions, H have poles only at zeros of and and poles of F and G, and those 1-points of F and G whose multiplicities are distinct from the multiplicities of corresponding 1-points of G and F respectively. Thus, we deduce from (10) that

(11)

here is the counting function which only counts those points such that but.

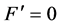
Because F and G share 1 IM, it is easy to see that

(12)

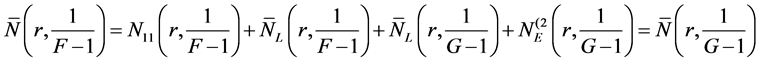
By the second fundamental theorem, we see that

(13)

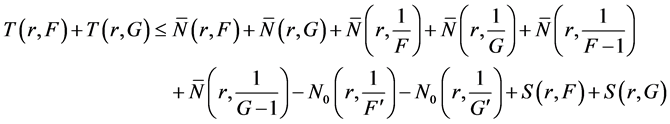
Using Lemma 2.2 and (11), (12) and (13), we get

(14)

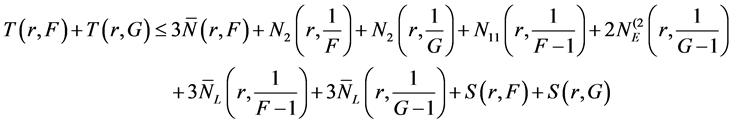
We discuss the following three sub cases.

Sub case 1.1.. Obviously.

(15)

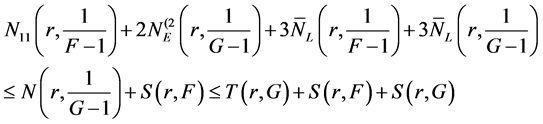
Combining (14) and (15), we get

(16)

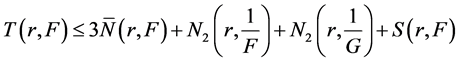
that is

By Lemma 2.1 for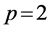, we get

So

which contradicts with (7).

Sub case 1.2.. It is easy to see that

(17)

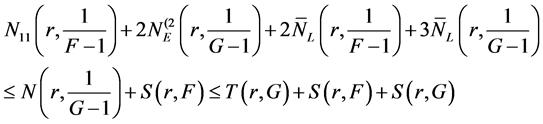
and

(18)

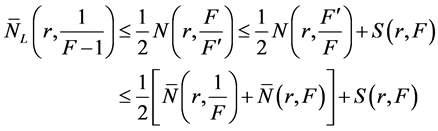
Combining (14) and (17) and (18), we get

(19)

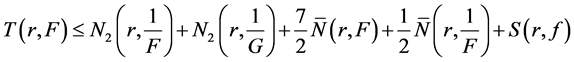
that is

By Lemma 2.1 for, we get

So

which contradicts with (8).

Sub case 1.3.. It is easy to see that

(20)

(21)

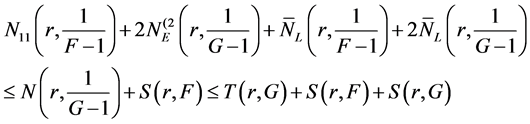
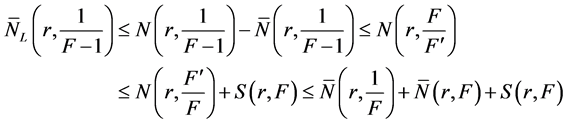
Similarly we have

(22)

Combining (14) and (20)-(22), we get

(23)

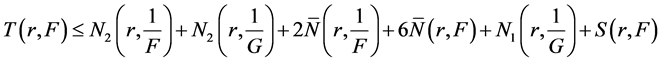
that is

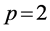
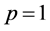
By Lemma 2.1 for and for respectively, we get

So

which contradicts with (9).

Case 2. Let

on integration we get from (10)

(24)

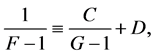
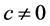
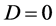
where C, D are constants and. we will prove that.

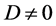
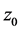
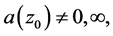
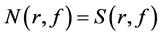
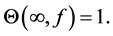
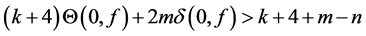
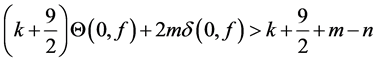
Sub case 2.1. Suppose. If be a pole of f with multiplicity p such that then it is a pole of G with multiplicity respectively. This contradicts (24). It follows that and hence Also it is clear that From (7)-(9) we know respectively

(25)

(26)

and

(27)

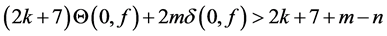
Since, from (24) we get

Suppose.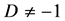

Using the second fundamental theorem for F we get

i.e.,

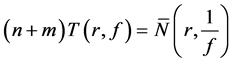
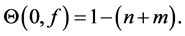
So, we have and so which contradicts (25)-(27).

If then

(28)

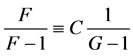
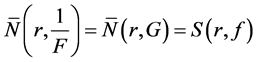
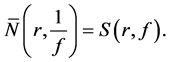
and from which we know and hence, If

We know from (28) that

So from Lemma 2.1 and the second fundamental theorem we get

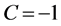
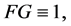
which is absurd. So and we get from (28) that which implies

In view of the first fundamental theorem, we get from above

which is impossible.

Sub case 2.2. 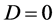and so from (24) we get

If 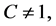then

and

By the second fundamental theorem and Lemma 2.1 for 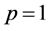and Lemma 2.3 we have

Hence

So, it follows that

and

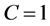
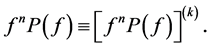
This contradicts (7)-(9). Hence and so that is This completes the proof of the theorem.

Cite this paper

Harina P. Waghamore,S. Rajeshwari, (2015) On Meromorphic Functions That Share One Small Function of Differential Polynomials with Their Derivatives. Applied Mathematics,06,2004-2013. doi: 10.4236/am.2015.612178

References