Applied Mathematics
Vol.06 No.10(2015), Article ID:59734,12 pages
10.4236/am.2015.610153
Supply Chain Commitment Contract Model Based on Uncertainty Theory under Uncertain Market Information
Yuquan Cui, Xiaolin Zhang, Xi Lu
School of Mathematics, Shandong University, Jinan, China
Email: cuiyq@sdu.edu.cn
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 10 August 2015; accepted 15 September 2015; published 18 September 2015
ABSTRACT
Based on the uncertainty theory, market demand information updating as the background, we study the coordination and optimization problem of three-stage supply chain in this paper. In half a asymmetric market information, participants are risk neutral; under the situation of the manufacturers and wholesalers having twice pre-season decision-making opportunity, wholesalers can be replenished in the season; manufacturers join the lowest supply contract of commitment: manufacturers for exchanging the information that they cannot get directly from the market will promise wholesalers to have a season lowest supply in pre-season. According to this contract, we establish optimization models of manufacturers and wholesalers respectively, and get the optimal strategy of supply chain members by analyzing the supply chain system. Finally, by giving a numerical example and comparing the results with that under random circumstances, the result is reasonable.
Keywords:
The Uncertainty Theory, Supply Chain, Commitment Contract, Information Updates

1. Introduction
The uncertainty theory [1] has been developed and improved constantly for more than ten years, since Professor Liu Baoding, Tsinghua University and his team put forward it. Its theoretical system was recognized and accepted gradually by the majority of scholars and experts, and part of them have put themselves in studying this theory [2] [3] . At present, axiom system of the theory has been established on the whole, and its theoretical system has been extended to planning theory, risk analysis, reliability analysis, logical reasoning, differential equations, statistics and differential and integral calculus and other fields. Its scope of application is expanding gradually; it has many examples of applications and the potential for further development in the fields of business, social, economic and financial. This paper considers applying the uncertainty theory to problems of the supply chain, to convert problem of random demand in the supply chain to that of uncertainty demand. At the beginning of entering the market, we do not know the actual needs of some items. Production enterprises can only accord to the experience and some experts predict if they want to grasp the market demand. Therefore, from this perspective, uncertain demand is closer to the actual than random demand. The problem of supply chain is old, and its earliest research can be traced back to 1888 when economist Edgeworth studied the supply chain shape, newsboy model [4] , with sales activities of seasonal merchandise which is more standard simplified. In the 1950s, with most of the lack of production and living materials because of the war, newsboy model and more complex models gradually became the object of research scholars, and was widely used in production of various industries [5] . Price effects were first introduced in newsboy model by Whitin [6] . The relationship between demand function and price made the sales price become one of the decision variables. Schweitzer and Cachon [7] analyzed the newsboy with preference on policy makers and found that the decisions were different from policy makers with different risk appetite, algorithms, forecasting and other factors, and thus the profits deviated from maximum profit to a certain extent. Porteus [8] , Silver [9] and some others summarized the newsboy model.
With further research, we got to know and researched Stackelberg game behavior in the supply chain and problems of supply chain coordination generated. Malone and Crowston [10] made the definition of supply chain coordination that was interdependence between the various acts of management. Hoppe [11] gave the definition of a coordinated multi-dimensional model based on the definition of Malone, enabling simultaneous information flow, logistics, and capital flow coordination, which could implement information flow, logistics, and capital flow coordination at the same time. Cachon [12] turned to the most simple newsboy model, continually improved the model and made it more complex. For an example, the wholesalers regard selling price and order quantity as decision variables. He expanded his study from the system of a manufacturer and a retailer to the system of a manufacturer and multiple retailers; retailers that face infinity and the uncertainty of market demand can be the constant replenishment instantaneously from the manufacturer and so on. These kinds of circumstances of supply chain coordination are discussed. He also discussed the supply chain coordination in these cases. Ying Wei and Tsan-Ming Choi [13] analyzed its mean-variance under the supply chain coordination mechanism of the Wholesale Pricing Contract and Profit Sharing Contract in another way and noted that Stackelberg game had a unique equilibrium point under the decentralized decision when the supply chain took such a mechanism. Cai Jianhu [14] gave the definition of flexibility contracts after studying a variety of supply chain contracts: the supply chain contract that could achieve the entire supply chain coordination while owing the capacity of distributing the gross profit of the supply chain between supply chain members in any way, and further illustrated the Order Quantity Contract, the Wholesale Price Contract and Revenue Sharing Contract are flexible contracts.
Numerous studies illustrate that it is indeed effective strategy that using such Revenue Sharing Contract, Quantity Flexibility Contract, the Wholesale Price Flexibility Contract, the Commitment Contract and the Option Contract in order to achieve supply chain system coordinated, no matter analyzing from either the perspective of the manufacturer and wholesaler or the perspective of a multi-stage supply chain or multi-level one. With consumers’ “battle” intensified, relationship between supply chain members also began to develop from the original simple division of profit to mutual benefit and win-win results. The members can gain more profits only by improving the competitiveness of the entire supply chain, so it has become hot spots of researches that the relational contract is concerned about the relationship between supply chain members. Relational contract is a convention, more accurately, a trust that could not specified by stringent legal provisions. Therefore the commitment itself may be unlike the general traditional contract that can put into effect through a simple contract. Wang Yingjun [15] defined the relational contract: the relevant provisions that ensured buyers and sellers to coordinate and optimize the sales channel performance by providing the proper information and incentive measures. Baker [16] studied the interaction between clear contracts and subtle ones. Tunay I. Tunca [17] analyzed the difference and gained the interaction mechanism between the two kinds of contracts based on Baker’s research. Dyrer and Chu [18] indicated that Relational Contract could effectively reduce the possibility of supply chain members adopting opportunistic behavior, enhance mutual trust between the members, thereby improve information sharing and reduce asymmetric information by analyzing the drawbacks of opportunistic decision behavior. Sun Yuanxin and in Mao recommended [19] summarized the main features of relational contract, including embedded relation, self-compliance, long-term time, the openness of terms, and noted that the safeguards of Relational Contract implementation: value of future cooperation, reputation and relationship rules. In addition, existing researches will also be summarized as follows: Relational Contract as an alternative of formal ones, Governance of Relational Contract, the use of relational contract in incentives. There are more researches on Relational Contracts, such as Zhao Pinghan [20] , Li Ying [21] , Diana Yan Wu [22] , Spengler [23] , Kannan Govindan [24] and so on.
The commitment contract is a typical relational contract. Helper [25] , Dyers and Ouchi [26] , Helper and Sako [27] et al. compared business strategies between the local enterprises and foreign-funded ones in the study and found that the biggest difference was the different commitment quantity and information sharing amount. Obviously they both are related to the trust degree between each other. Studies have shown that the larger commitment quantity and information shared between supply chain members, the lower uncertainties and costs of the entire supply chain will be. Applying its conclusion to the real world, the manufacturer will reduce the number of wholesalers to some extent in order to increase its commitment amount for wholesalers as much as possible without exceeding its production capacity. On the other hand, the wholesaler will improve its degree of information sharing to exchange. Durango-Cohen and Yano [28] studied a commitment contract between ASIC manufacturers and customers, in which the manufacturer would commit a minimum supply quantity to a customer, when he provided a demand forecast and commit to buy some of them at least. Similar commitment contracts are also described in Tsay [29] , Tsay and Lovejoy [30] . Eppen and Iyer [31] have proposed a commitment contract on poor market, in which wholesalers have the right to pay only a part of its order quantity in advance when ordering and then choose to buy the remainder. Bassok [32] , Bassok and Anupindi [33] , Anupindi and Bassok [34] put forward some other commitment contracts in which the wholesalers updating the order quantity once again is allowed. Their application avoids the possibility of wholesalers exaggerating the market demand deliberately to a certain extent when sharing information and too low production of manufacturers.
Aiming to seasonal products with long production cycle, short sales period, unknown demand and large volatility, combining with the previous researches on the supply chain coordination with market demand information updates and based on the uncertainty theory, this paper further deepens and expands the application of commitment contract, which is a kind of relational contract, in the supply chain management. Based on the general newsboy model with uncertainty demand, this paper gives a two-stage supply chain model in case of market demand information updating and establishes the appropriate decision-making model from the perspective of the supply chain members (the manufacturer and the wholesaler) respectively, and then optimizes the corresponding supply chain contract with updating information from the two aspects.
Based on the lowest supply commitment contract, this paper establishes a two-stage three-stage supply chain system made up of a manufacturer and a wholesaler firstly: before the season beginning, the wholesaler and the manufacturer carry on the first time “blind” production and order. With the season coming, the wholesaler corrects the order quantity while he provides demand information with certain loyalty to the manufacturer. At the same time, the manufacturer of production revised inventory and promised the lowest supply. After the season beginning, the wholesaler can carry on replenishing once again according to the situation. Based on the supply chain above, this paper establishes the optimal decision model for the manufacturer and the wholesaler respectively and ultimately gets the wholesaler’s optimal order quantity, the value of the manufacturer’s optimal commitment, the optimal production quantity and other strategic decisions. Finally, it gives exponential analysis and obtains a more realistic conclusion.
2. Preliminary Model
2.1. Symbol Description
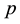 : The market price of the commodity.
: The market price of the commodity.
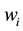 : The manufacturer’s wholesale price in the stage
: The manufacturer’s wholesale price in the stage 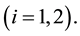
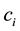 : Cost of the manufacturer’s production in the i-th stage.
: Cost of the manufacturer’s production in the i-th stage.
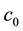 : Cost of implementation per unit of semi-finished products.
: Cost of implementation per unit of semi-finished products.
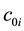 : The manufacturer’s cost of production per unit semi-finished in the stage.
: The manufacturer’s cost of production per unit semi-finished in the stage.
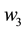 : Wholesaler’s replenishment wholesale price in the sales cycle.
: Wholesaler’s replenishment wholesale price in the sales cycle.
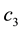 : Unit production cost when manufacturer start an emergency production in the sales season.
: Unit production cost when manufacturer start an emergency production in the sales season.
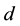 : Total pre-season order quantity of wholesaler.
: Total pre-season order quantity of wholesaler.
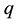 : Manufacturer’s total pre-season production inventory quantity.
: Manufacturer’s total pre-season production inventory quantity.
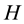 : Manufacturer’s total amount of pre-season semi-finished.
: Manufacturer’s total amount of pre-season semi-finished.
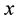 : Market demand, an uncertain variable
: Market demand, an uncertain variable 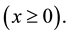
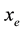 : The amount of market demand update
: The amount of market demand update 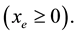
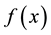 : Uncertain density function of the uncertain demand under normal state.
: Uncertain density function of the uncertain demand under normal state.



2.2. Model Description
Definition 1 [Liu1]: The uncertainty distribution Φ of an uncertain variable 

Definition 2 [Liu1]: An uncertain variable 



Definition 3 [Liu1]: Let 


provided that at least one of the two integrals is finite.
Theorem 1[Liu1]: Let 


Based on the newsboy model, a production enterprise with unit production costs C, unit retail price P(P > C), D is stochastic market demand that policy makers facing. 


Calculating its derivative, we get


It means that 



In the situation that information of market demand is uncertain and updating, as manufacturers can’t contact with the market, they get the updated information only through information sharing with wholesalers. Note 


Phase 1: Manufacturers and wholesalers confirm uncertainty distribution of market demand with years of experience in sales and expert assessment, denoting as 





Phase 2: With the sales season approaching, wholesalers get the market updates



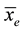










Phase 3: With the sales season starting, we can get the market demand x, wholesalers selectively emit replenishment orders to manufacturers to resive the final order quantity according to the total order quantity d and demand x. As a manufacturer, they can only mechanically do their ability to distribute the surplus goods to wholesalers as complement goods. If the market needs are not met, give manufacturers and wholesalers s punishment considering loss from the customer, loss of reputation and so on. It is called shortage punishment.
Known from the above analysis, for a manufacturer, the quantity he committed must be greater than the wholesalers amount in the first two stages, that is,


that caused by understanding updates insufficiently. That caused by limited production is 
Wholesalers take initiative relatively in the supply chain system and manufacturers make decisions due to the behavior of wholesalers. We assume that wholesalers know the manufacturers different responses to different



2.3. The Optimization Model of Manufacturers Based on That Commitment Contract with Changing Demand Information
Known from a series of analysis above, we should set about from manufacturers. Obviously the order quantities were known in the two production decisions, so 



It should be noted that manufacturers need not make any decisions in phase III, the producers do not need to make any decisions considering the collaboration process in the entire supply chain. Decomposing the expression by the stages of production decision and combining stage II and stage III, we can get the optimization model of manufacturer’s expected profits in this situation:

In which,

Analyzing the model above in the reverse order, we can analyze the decision problem in view of the stage II and solve 


Theorem 2: In the decision problem 


Proof: reducing decision problem:
In the decision problem


Discussing different circumstances:
When

(i) When





(ii) When

uncertain distribution function,





(iii) When

the second term in the expression of 

way, we take the derivative of C. Then we get

That is, 

When

In this case, since the total production has exceeded the amount of updating information


(i) When




(ii) When

To sum up, the manufacturers’ the most optimal minimum commitment supply quantity satisfies 

Known from Theorem 2, the manufacturer will choose to avoid shortage punishment 

Based on these, we continue to analyze the optimal production capacity q.
Theorem 3: In the second stage of the decision problem


In which





Proof: Compute the expectation of 

Here 

Discussing different circumstances:
When

When

From the nature of condition uncertain distributed function, we know



When

As

So only let





When

When




When



To sun up, the decision problem in the second stage has 4 possible optimal strategy, noting as

Integrating above analysis, Theorem 2 and Theorem 3, at the beginning of stage II, the manufacturer obtain two decision programs for both strategies 






2.4. Optimization Model of Wholesalers with Demand Information Updates Based on the Commitment Contract
Relative to the manufacturers and wholesalers have been in a dominant position throughout the entire supply chain operation process. They take the initiate to carry on two pre-season orders, obtain the market information directly, selectively share it with the manufacturer, and understand the manufacturer’s response to update information. That is, they now how the manufacturer correct the demand distribution function 

Here 

in which

Here 





Theorem 4: In the second stage, the optimal pre-season order quantity that wholesalers selected is


Proof: Simplify the decision problem and get

It is necessary to pay attention to that 



Discussing different circumstances:
When C = q,
(i) When q = d, we have

(1) if

Computing its derivation to d, we can get


In this case, 
if

In this case, in order to maximize

(ii) When

Here the second term and the fourth one are independent of d.
If

And we can get further

In the similar way, we obtain the optimal decision is
If

At this moment, in order to maximize

b) When
(i) When


whose the last term is independent of d.
(1) if

So we have 



(2) if

At this moment, in order to maximize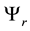

(ii) When
or
Instruction: For a wholesaler, when choosing the optimal pre-season order quantity d from 


2.5. Optimization Analysis of Supply Chain Based on the Commitment Contract with Information Updates
From the analysis in above part 2 and part 3, we get that in order to achieve coordination, supply chain should have the following conclusions, when the commitment amount C satisfy certain conditions.
Completion 1: Under the condition C = q, when



Proof: Under the condition C = q when




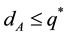
should have


When q = d and









Completion 2: Under the condition




Proof: Under the condition 








chain, we should have



only to adjust











Known from the above two completion and above analysis, when the manufacturer’s optimal production is larger than the wholesaler’s optimal order quantity, it is impossible to achieve optimal state of both of two members of the supply chain. Only one of them can be optimal, and the other will have some extra expense. In order to achieve the supply chain coordination, deduce more costs the other member paid from the more part of the profit the optimal member get than that without cooperation and the two members negotiate to allocate this part profits. Then the supply chain coordination can be achieved; when the manufacturer’s production is equal to the wholesaler’s order quantity, the supply chain coordination can be achieved. The two sides can reach optimal state under some conditions.
On the other hand, the total profits of the manufacturer is

Computing the derivative of the above formula, at this time it is necessary that 


This completion is to reach the optimal supply chain coordination in the case of q = d. It is similar with the process of get the optimal order quantity
3. Exponential Analysis
We assume that before market information updates, the manufacturer and wholesaler analyze and estimate that the market demand obey the normal uncertainty distribution










The wholesaler reflects to market information honestly. Here there is
As an manufacturer,

The manufacturer gives a larger

As a manufacturer, 





If the manufacturer does not consider new information the wholesaler provided, he still think
As a manufacturer, 
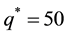




Comparing the three cases above, we get the first one is the optimal and its cost is the lowest.
In addition, if complete the previous analyzed based on the probability theory, its result in the first case is as follows:
As a manufacturer,



Compared with results obtained in the previous uncertainty theory, the optimal production value of the manufacturer’s is less slightly and the optimal value of wholesalers is less than the previous value.
The calculation is similar in the other two cases, so here we do not compare them.
4. Conclusion
Based on the uncertainty theory, this paper studies seasonal merchandise with long production cycle, relatively short marketing period, uncertain and strong volatile market demand. Setting about the perspective of market demand information updated, it analyzes the contract coordination problem of a two-stage three-stage supply chain system with a risk-neutral manufacturer and a risk-neutral wholesaler. In the system of pure contract supply chain, it cannot achieve coordination. It introduces the pledge contract, in the case that producers have twice pre-season production and wholesalers have twice pre-season order and a replenishment opportunity in the season. It established contract model respectively, and according to these models, it carried on the optimization analysis. The optimal quantity, the output of eugenics and the optimal amount of commitment of the supply chain members are presented. In the case of the wholesalers predomination, it gives the information sharing strategies that regulate the supply chain. In this paper, it is just an attempt to apply the uncertainty theory in supply chain. There may also be many problems, but after all, it has been applied to the practical problem. I believe it will be applied to analyze the supply chain system by more researchers.
Cite this paper
YuquanCui,XiaolinZhang,XiLu, (2015) Supply Chain Commitment Contract Model Based on Uncertainty Theory under Uncertain Market Information. Applied Mathematics,06,1727-1739. doi: 10.4236/am.2015.610153
References
- 1. Liu, B. (2007) Uncertainty Theory. 2nd Edition, Spring-Verlag, Berlin.
http://dx.doi.org/10.1007/978-3-540-73165-8_5 - 2. Li, X. and Liu, B. (2009) Hybrid Logic and Uncertain Logic. Journal of Uncertain Systems, 3, 83-94.
- 3. Liu, Y.H. (2013) Uncertain Random Variables: A Mixture of Uncertainty and Randomness. Soft Computing, 17, 625-634.
http://dx.doi.org/10.1007/s00500-012-0935-0 - 4. Edgeworth, F.Y. (1888) The Mathematical Theory of Banking. Journal of Royal Statistical Society, 51, 113-127.
- 5. Gallego, G. and Moon, I. (1993) The Distribution Free Newsboy Problem: Review and Extensions. The Journal of the Operational Research Society, 44, 825-834.
http://dx.doi.org/10.1057/jors.1993.141 - 6. Whitin, T.M. (1955) Inventory Control and Price Theory. Management Science, 2, 61-68.
http://dx.doi.org/10.1287/mnsc.2.1.61 - 7. Schweitzer, M.E. and Cachon, G.P. (2000) Decision Bias in the Newsvendor Problem with a Known Demand Distribution: Experimental Evidence. Management Science, 46, 404-420.
http://dx.doi.org/10.1287/mnsc.46.3.404.12070 - 8. Porteus, E.L. (1990) Foundations of Stochastic Inventory Theory. In: Heyman, D.P. and Sobel, M.J., Eds., Handbooks in Operations Research and Management Science, Vol. 2, Ch. 12, Elsevier Science Publishers, Amsterdam, 605-652.
- 9. Silver, E.A., Pyke, D.F. and Peterson, R. (1998) Inventory Management and Production Planning and Scheduling. 3rd Edition, John Wiley, New York.
- 10. Malone, T.W. and Crowstom, K. (1994) The Interdisciplinary Study of Coordination. ACM Computing Surveys, 16, 87-119.
- 11. Hoppe, R.M. (2001) Outlining a Future of Supply Chain Management-Coordinated Supply Network. Master’s Thesis, Civil Engineering Tufts University, Medford.
- 12. Cachon, G.P. (2001) Supply Chain Coordination with Contracts. In: Graves, S.C. and de Kok, A.G., Eds., Handbooks in Operations Research and Management Science: Supply Chain Management, Vol. 11, Elsevier, Amsterdam.
- 13. Wei, Y. and Choi, T.-M. (2010) Mean-Variance Analysis of Supply Chains under Wholesale Pricing and Profit Sharing Schemes. European Journal of Operational Research, 204, 255-262.
http://dx.doi.org/10.1016/j.ejor.2009.10.016 - 14. Cai, J.H. (2011) Supply Chain Management under Uncertainty Government. Technology Press, Beijing.
- 15. Wang, Y.J. (2001) Practical Modeling in Supply Chain Management and Data Mining. Tsinghua University Press, Beijing.
- 16. Baker, G., Gibbons, R. and Murphy, K.J. (1994) Subjective Performance Measures in Optimal Incentive Contracts. The Quarterly Journal of Economics, 109, 1125-1156.
http://dx.doi.org/10.2307/2118358 - 17. Tunca, T.I. and Zenios, S.A. (2006) Supply Auctions and Relational Contracts for Procurement. Manufacturing and Service Operations Management, 8, 43-67.
http://dx.doi.org/10.1287/msom.1060.0097 - 18. Dyrer, J.H. and Chu, W. (2003) The Role of Trustworthiness in Reducing Transaction Costs and Improving Performance: Empirical Evidence from the United States, Japan, and Korea. Organization Science, 1, 57-68.
http://dx.doi.org/10.1287/orsc.14.1.57.12806 - 19. Sun, Y.X. and Yu, M.J. (2010) Relational Contract Research Review. Academic Communication, 8, 117-123.
- 20. Zhao, H.P., Feng, Y.C., Yao, L.G. and Jiang, J.-D. (2005) An Analysis on Supply Chain Coordination with Target Quantity Rebate. Systems Engineering, 23, 51-55.
- 21. Li, Y. (2012) Research on Dynamics of Relationship Contract Governance. Inquiry into Economic Issues, 8, 90-94.
- 22. Wu, D.Y. (2013) The Impact of Repeated Interactions on Supply Chain Contracts: A Laboratory Study. International Journal of Production Economics, 142, 3-15.
- 23. Spengler, J. (1950) Vertical Integration and Antitrust Policy. Political Economy, 58, 347-352.
http://dx.doi.org/10.1086/256964 - 24. Govindan, K., Diabat, A. and Popiuc, M.N. (2012) Contract Analysis: A Performance Measures and Profit Evaluation within Two-Echelon Supply Chains. Computers Industrial Engineering, 63, 58-74.
http://dx.doi.org/10.1016/j.cie.2012.01.010 - 25. Helper, S. (1991) How Much Has Really Changed between US Manufacturers and Their Suppliers. Sloan Management Review, 32, 15-28.
- 26. Dyers, H. and Ouchi, W. (1993) Japanese-Style Partnerships: Giving Companies a Competitive Edge. Sloan Management Review, 35, 51-64.
- 27. Helper, S. and Sako, M. (1995) Supplier Relations in Japan and the United States: Are the Converging. Sloan Management Review, 36, 77-85.
- 28. Durango-Cohen, E.J. and Yano, C.A. (2006) Supplier Commitment and Production Decisions under a Forecast Commitment Contract. Management Science, 52, 54-67.
http://dx.doi.org/10.1287/mnsc.1050.0471 - 29. Tsay, A. (1999) The Quantity Flexibility Contract and Supplier-Customer Incentives. Management Science, 45, 1339-1358.
http://dx.doi.org/10.1287/mnsc.45.10.1339 - 30. Tsay, A. and Lovejoy, W.S. (1999) Quantity Flexibility Contracts and Supply Chain Performance. Journal of Manufacturing and Service Operation Management, 1, 89-101.
http://dx.doi.org/10.1287/msom.1.2.89 - 31. Eppen, G. and Iyer, A. (1997) Backup Agreements in Fashion Buying—The Value of Upstream Flexibility. Management Science, 43, 1469-1484.
http://dx.doi.org/10.1287/mnsc.43.11.1469 - 32. Bassok, Y., Srinivasan, R., Bixby, A. and Wiesel, H. (1997) Design of Component Supply Contracts with Commitment Revision Flexibility. IBM Journal of Research and Development, 41, 693-702.
http://dx.doi.org/10.1147/rd.416.0693 - 33. Sassok, Y. and Anupindi, R. (1997) Analysis of Supply Contracts with Commitments and Flexibility. Northwestern University, Evanston.
- 34. Anupindi, R. and Bassok, Y. (1998) Approximations for Multiproduct Contracts with Stochastic Demands and Business Volume Discounts: Single Supplier Case. IIE Transactions, 30, 723-734.
http://dx.doi.org/10.1080/07408179808966518





