Received 10 February 2015; accepted 10 March 2015; published 11 March 2015

ABSTRACT

In this paper we developed a fuzzy inventory model for deteriorating items with time dependent demand rate. Shortages are allowed and completely backlogged. The backlogging rate of unsatisfied demand is assumed to be a decreasing exponential function of waiting time. The demand rate, deterioration rate and backlogging rate are assumed as a triangular fuzzy numbers. The purpose of our study is to defuzzify the total profit function by signed distance method and centroid method. Further a numerical example is also given to demonstrate the developed crisp and fuzzy models. A sensitivity analysis is also given to show the effect of change of the parameters.

Keywords:

Inventory, Deterioration, Shortages, Triangular Fuzzy Number, Signed Distance Method and Centroid Method

1. Introduction

In many inventory models uncertainty is due to fuzziness and fuzziness is the closed possible approach to reality. In recent years some researchers gave their attention towards a time dependent rate because the demand of newly launched products such as fashionable garments, electronic items, mobiles etc. increases with time and later it becomes constant. Deterioration is defined as damage, decay or spoilage of the items that are stored for future use always loose part of their value with passage of time, so deterioration cannot be avoided in any business scenarios. F. Harris (1915) [1] developed first inventory model. Lotfi A. Zadeh (1965) [2] introduced the concept of fuzzy set theory in inventory modeling. L. A. Zadeh [3] and R. E. Bellman (1970) considered an inventory model on decision making in fuzzy environment. R. Jain (1976) [4] developed a fuzzy inventory model on decision making in the presence of fuzzy variables. D. Dubois and H. Prade (1978) [5] defined some operations on fuzzy numbers. J. Kacpryzk and P. Staniewski (1982) [6] developed an inventory model for long term inventory policy making through fuzzy decisions. H. J. Zimmerman (1983) [7] tried to use fuzzy sets in operational research. G. Urgeletti Tinarelli (1983) [8] considered the inventory control models and problems. K. S. Park (1987) [9] define the fuzzy set theoretical interpretation of an EOQ problem. M. Vujosevic, D. Petrovic and R. Petrovic (1996) [10] developed an EOQ formula by assuming inventory cost as a fuzzy number. J. S. Yao and H. M. Lee (1999) [11] developed a fuzzy inventory model by considering backorder as a trapezoidal fuzzy number. C. K. Kao and W. K. Hsu (2002) [12] developed a single period inventory model with fuzzy demand. C. H. Hsieh (2002) [13] developed an inventory model and give an approach of optimization of fuzzy production. J. S. Yao and J. Chiang (2003) [14] developed an inventory model without backorders and defuzzified the fuzzy holding cost by signed distance and centroid methods. Sujit D. Kumar, P. K. Kund and A. Goswami (2003) [15] developed an economic production quantity model with fuzzy demand and deterioration rate. J. K. Syed and L. A. Aziz (2007) [16] consider the signed distance method for a fuzzy inventory model without shortages. P. K. De and A. Rawat (2011) [17] developed a fuzzy inventory model without shortages by using triangular fuzzy number. C. K. Jaggi, S. Pareek, A. Sharma and Nidhi (2012) [18] developed a fuzzy inventory model for deteriorating items with time varying demand and shortages.

Sumana saha and Tripti Chakrabarty (2012) [19] developed a fuzzy EOQ model with time varying demand and shortages. D. Dutta and Pawan Kumar (2012) [20] considered a fuzzy inventory model without shortages using a trapezoidal fuzzy number. D. Dutta and Pawan Kumar (2013) [21] [22] considered an optimal replenishment policy for an inventory model without shortages by assuming fuzziness in demand, holding cost and ordering cost. Dipak Kumar Jana, Barun Das and Tapan Kumar Roy (2013) [23] give a fuzzy generic algorithm approach for an inventory model for deteriorating items with backorders under fuzzy inflation and discounting over random planning horizon.

In this paper we consider an inventory model for deteriorating items with time dependent demand rate and partial backlogging. Shortages are allowed and completely backlogged for the next replenishment cycle. The demand rate, deterioration rate and backlogging rate are assumed as triangular fuzzy numbers. The purpose of our study is to defuzzify the total profit function by signed distance method and centroid method and comparing the results of these two methods with the crisp model. Figure 1 shows the developed model and Figure 2 and Figure 3 show the graphs of total profit function with respect to deterioration and backlogging rates.

2. Definitions and Preliminaries

When we are considering the fuzzy inventory model then the following definitions are needed.

(1) A fuzzy set 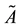on the given universal set 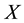is denoted and defined by

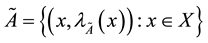
where, 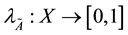, is called the membership function,

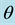And, 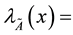degree of 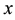in.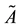

(2) A fuzzy number 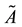is a fuzzy set on the real line, if its membership function 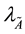has the following properties

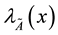is upper semi continuous.

, outside some interval.

real numbers and, such that is increasing on, decreasing on and, for each in.

(3) A triangular fuzzy number is specified by the triplet where and defined by its continuous membership function as follows

(4) Let be a fuzzy set defined on, then the signed distance of is defined as

where, , is an α cut of a fuzzy set.

(5) If is a triangular fuzzy number then the signed distance of is defined as.

(6) If is a triangular fuzzy number then the centroid method on is defined as.

3. Assumptions and Notations

We consider the following assumptions and notations.

The demand rate is where is a positive constant, for a increasing demand, and for a decreasing demand.

1. is the deterioration parameter.

2. is the backlogging parameter.

3. is the ordering cost per order.

4. is the holding cost per unit per unit time.

5. is the deterioration cost per unit per unit time.

6. is the shortages cost per unit per unit time.

7. is the purchase cost per unit.

8. is the selling price per unit, where.

9. is the opportunity cost per unit due to lost sales.

10. is the length of order cycle.

11. is the fuzzy deterioration parameter.

12. is the fuzzy backlogging parameter.

13. is the fuzzy demand parameter.

14. is the total fuzzy profit per unit time.

15. is the time at which shortage starts.

16. is the total profit per unit time.

17. is the inventory level at any time in.

18. The inventory system consists only one item.

19. The time horizon is infinite.

20. The lead time is zero.

21. The replenishment rate is infinite.

3.1. Mathematical Formulation

Suppose an inventory system consists units of the product in the beginning of each cycle. Due to demand and deterioration the inventory level decreases in and becomes zero at. The interval is the shortages interval. During the shortages interval the unsatisfied demand is backlogged at a rate of, where is the waiting time.

The instantaneous inventory level at any time in are governed by the following differential equations

(1)

with boundary condition

(2)

with boundary condition

(3)

The solution of Equation (1) is

(4)

The solution of Equation (2) is

(5)

using, in Equation (3)

(6)

The ordering cost per cycle is

(7)

The holding cost per cycle is

(8)

The deterioration cost per cycle is

(9)

The shortage cost per cycle is

(10)

The purchase cost per cycle in is

(11)

The purchase cost per cycle in is

(12)

Due to lost sales the opportunity cost per cycle in is

(13)

The sales revenue cost per cycle in is

(14)

Therefore the total profit per unit time is

(15)

For a Ist order approximation of

(16)

The necessary condition for to be maximum is that and, and

solving these equations we find the optimum values of and say and for which profit is maxi- mum and the sufficient condition is

and.

(17)

(18)

3.2. Fuzzy Model

Let us consider the inventory model in fuzzy environment due to uncertainty in parameters let us assume that the parameters, and may change within some limits.

Let, and are triangular fuzzy numbers then the total profit per unit time in fuzzy sense is

(19)

Now we defuzzify the total profit in two cases.

3.2.1. Signed Distance Method

By signed distance method the total profit per unit time is

(20)

where,

From Equation (20) we have

(21)

The necessary condition for to be maximum is that and, and

solving these equations we find the optimum values of and say and for which profit is maximum and the sufficient condition is

and.

(22)

(23)

3.2.2. Centroid Method

By Centroid method the total profit per unit time is

(24)

(25)

The necessary condition for to be maximum is that and, and

solving these equations we find the optimum values of and say and for which profit is maximum and the sufficient condition is

and

(26)

(27)

3.3. Numerical Example

Let us consider an inventory system with the following parameters in appropriate units as

, , ,

, ,.

Table 1 shows that as we increase deterioration parameter then the total profit increases.

Table 2 shows that as we increase backlogging parameter then the total profit increases.

Table 3 shows that as we increase demand parameter then the total profit increases.

3.3.1. Fuzzy Model

Let, and are triangular fuzzy numbers.

The solution of the fuzzy inventory model can be determined by the following two methods.

3.3.2. Signed Distance Method

When, and are triangular fuzzy numbers, then Table 4 shows the value of total profit.

When and are triangular fuzzy numbers, then Table 5 shows the value of total profit.

When and are triangular fuzzy numbers, then Table 6 shows the value of total profit.

3.3.3. Centroid Method

When, and are triangular fuzzy numbers, then Table 7 shows the value of total profit.

When and are triangular fuzzy numbers, then Table 8 shows the value of total profit.

When and are triangular fuzzy numbers, then Table 9 shows the value of total profit.

4. Sensitivity Analysis

From Table 1, we see that as we increase the deterioration parameter then the optimal time period, the optimal cycle time and total profit increases.

From Table 2, we see that as we increase the backlogging parameter then the optimal time period, the optimal cycle time decreases and total profit increases.

From Table 3, we see that as we increase the demand rate parameter then the optimal time period decreases and the optimal cycle time and total profit increases.

In the case of crisp model we see that the backlogging parameter is more sensitive than the deterioration parameter and the demand rate parameter.

From the tables for signed distance method and centroid method we see that the fuzzy variables and are more sensitive than the fuzzy variable. As we increase the fuzzy variables and in the signed distance method and centroid method than the total profit increases rapidly in centroid method. Therefore in the sense of fuzziness the centroid method is better one than the signed distance method.

5. Conclusion

In this paper we studied a fuzzy inventory model for deteriorating items with time dependent demand rate and partial backlogging. Shortages are allowed and completely backlogged. As we increase the parameters, and in the crisp model then the total profit increases and due to the uncertainties in the demand rate, deterioration rate and backlogging rate the parameters, and are consider as triangular fuzzy numbers. For defuzzification by signed distance method and centroid method it has been observed that the total profit decreases as the optimal cycle time decreases and the profit given by the signed distance method is minimum as compared to the centroid method. Further this model can be generalized by considering time dependent deterioration rate, holding cost, shortage cost and so many types.

Acknowledgements

The author would like to thank anonymous referees for their valuable comments and suggestions for the improvement of this paper.

Cite this paper

SushilKumar,U. S.Rajput, (2015) Fuzzy Inventory Model for Deteriorating Items with Time Dependent Demand and Partial Backlogging. Applied Mathematics,06,496-509. doi: 10.4236/am.2015.63047

References

NOTES

^*Corresponding author.