Applied Mathematics
Vol.06 No.02(2015), Article ID:53795,20 pages
10.4236/am.2015.62026
Complete Semigroups of Binary Relations Defined by Semilattices of the Class 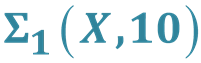
Shota Makharadze1, Neşet Aydın2, Ali Erdoğan3
1Shota Rustavelli University, Batum, Georgia
2Çanakkale Onsekiz Mart University, Çanakkale, Turkey
3Hacettepe University, Ankara, Turkey
Email: shota59@mail.ru, neseta@comu.edu.tr, alier@hacettepe.edu.tr
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 10 January 2015; accepted 28 January 2015; published 4 February 2015

ABSTRACT
In this paper we give a full description of idempotent elements of the semigroup BX (D), which are defined by semilattices of the class S1 (X, 10). For the case where X is a finite set we derive formulas by means of which we can calculate the numbers of idempotent elements of the respective semigroup.
Keywords:
Semilattice, Semigroup, Binary Relation

1. Introduction
Let X be an arbitrary nonempty set, D be an X-semilattice of unions, i.e. such a nonempty set of subsets of the set X that is closed with respect to the set-theoretic operations of unification of elements from D, f be an arbitrary mapping of the set X in the set D. To each such a mapping f we put into correspondence a binary relation 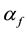 on the set X that satisfies the condition
on the set X that satisfies the condition
The set of all such 
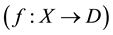 is denoted by
is denoted by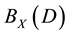 . It is easy to prove that
. It is easy to prove that 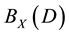 is a semigroup with respect to the operation of multiplication of binary relations, which is called a complete semigroup of binary relations defined by an X-semilattice of unions D.
is a semigroup with respect to the operation of multiplication of binary relations, which is called a complete semigroup of binary relations defined by an X-semilattice of unions D.
Recall that we denote by 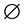 an empty binary relation or empty subset of the set X. The condition
an empty binary relation or empty subset of the set X. The condition 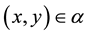 will be written in the form xαy. Further let
will be written in the form xαy. Further let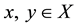 ,
, 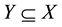 ,
, 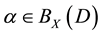 ,
, 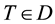 ,
, 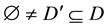 ,
, 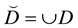 and
and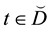 . Then by symbols we denoted the following sets:
. Then by symbols we denoted the following sets:
By symbol 
Definition 1. We say that the complete X-semilattice of unions D is an XI-semilattice of unions if it satisfies the following two conditions:
a) 

b) 
Definition 2. We say that a nonempty element T is a nonlimiting element of the set D' if 

Definition 3. Let




Note that, if 

1)
2) 


Let 
The following Theorems are well know (see [1] and [3] ).
Theorem 4. Let X be a finite set; δ and q be respectively the number of basic sources and the number of all automorphisms of the semilattice D. If 

where 
Theorem 5. Let D be a complete X-semilattice of unions. The semigroup 
Theorem 6. Let X be a finite set and 



representation 
a) 
b) 

c) 

Theorem 7. Let D, 




1) if 

a) 




b)
c) the equality 
2) if
a) 




b)
c) the equality 
Corollary 1. Let 








2. Idempotent Elements of the Semigroups 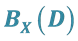
Let X and 


An X-semilattice that satisfies conditions (1) is shown in Figure 1.
Let 
Figure 1. Diagram of D.
are pairwise disjoint subsets of the set X and 
ping of the semilattice D onto the family sets

Here the elements P1, P2, P3, P4, P5, P6, P7, P8 are basis sources, the elements P0, P6, P9 are sources of completeness of the semilattice D. Therefore 

Lemma 1. Let


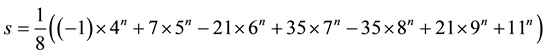
Proof. In this case we have: m = 10, δ = 7. Notice that an X-semilattice given in Figure 1 has eight automorphims. By Theorem 1.1 it follows that

where 

Example 8. Let 

Lemma 2. Let

1)
(see diagram 1 of the Figure 2);
2)
(see diagram 2 of the Figure 2);
3)
(see diagram 3 of the Figure 2);
4)
(see diagram 4 of the Figure 2);
5)
(see diagram 5 of the Figure 2);
6)
(see diagram 6 of the Figure 2);
7)
(see diagram 7 of the Figure 2);
8)
(see diagram 8 of the Figure 2);
9)
(see diagram 9 of the Figure 2);
10)
(see diagram 10 of the Figure 3);
11)
(see diagram 11 of the Figure 2);
12)
(see diagram 12 of the Figure 2);
13)
(see diagram 13 of the Figure 2);
14)
(see diagram 14 of the Figure 2);
15)
(see diagram 15 of the Figure 2);
16)
(see diagram 16 of the Figure 2);
17)
(see diagram 17 of the Figure 2);
18)
(see diagram 18 of the Figure 2);
19)
(see diagram 19 of the Figure 2);
20)
(see diagram 20 of the Figure 2);
21)
(see diagram 21 of the Figure 2);
22)
(see diagram 22 of the Figure 2);
23)
(see diagram 23 of the Figure 2);
24)
(see diagram 24 of the Figure 2);
25)
(see diagram 25 of the Figure 2);
26)
(see diagram 26 of the Figure 2);
27)
(see diagram 27 of the Figure 2);
28)
(see diagram 28 of the Figure 2);
29)
(see diagram 29 of the Figure 2);
30)
(see diagram 30 of the Figure 2);
31)
(see diagram 31 of the Figure 2);
32)
(see diagram 32 of the Figure 2);
33)
(see diagram 33 of the Figure 2);
34)
(see diagram 34 of the Figure 2);
35)
(see diagram 35 of the Figure 2);
36)
(see diagram 36 of the Figure 2);
37)
(see diagram 37 of the Figure 2);
38)
(see diagram 38 of the Figure 2);
39)
(see diagram 39 of the Figure 2);
40)
(see diagram 40 of the Figure 2);
41)
(see diagram 41 of the Figure 2);
42)
(see diagram 42 of the Figure 2);
43)
(see diagram 43 of the Figure 2);
44)
(see diagram 44 of the Figure 2);
45)
(see diagram 45 of the Figure 2);
46)
(see diagram 46 of the Figure 2);
47)
(see diagram 47 of the Figure 2);
48)
(see diagram 48 of the Figure 2);
Figure 2. Diagram of all subsemilattices of D.
49)
(see diagram 49 of the Figure 2);
50)
(see diagram 50 of the Figure 2);
51)
(see diagram 51 of the Figure 2);
52)
(see diagram 52 of the Figure 2);
Diagrams of subsemilattices of the semilattice D.
Lemma 3. Let
1)
(see diagram 1 of the Figure 2);
2)
(see diagram 2 of the Figure 2);
3)
(see diagram 3 of the Figure 2);
4)
(see diagram 4 of the Figure 2);
5)
(see diagram 5 of the Figure 2);
6)
(see diagram 6 of the Figure 2);
7)
(see diagram 7 of the Figure 2);
8)
(see diagram 8 of the Figure 2);
Proof. It is well know (see [1] ), that the semilattices 1 to 8, which are given by lemma 2 are always XI-semi- lattices. The semilattices 9 and 10 which are given by Lemma 2
(see diagram 9 of the Figure 2);
(see diagram 10 of the Figure 2);
are XI-semilattices iff the intersection of minimal elements of the given semilattices is empty set. From the formal equalities (1) of the given semilattice D we have
From the equalities given above it follows that the semilattices 9 and 10 are not XI-semilattices.
The semilattices 11
(see diagram 1-8 of the Figure 3);
are not XI-semilattice since we have the following inequalities
The semilattices 12 to 52 are never XI-semilattices. We prove that the semilattice, diagram 52 of the Figure 2, is not an XI-semilattice (see Figure 4). Indeed, let 
be a family of sets, where 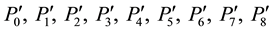
be a mapping of the semilattice Q onto the family of sets
Figure 3. Diagram of all subsemilattices which are isomorphic to 11 in Figure 2.
Figure 4. Diagram of subsemilattice 52 in Figure 2.

Here the elements 





We have, that 



We denoted the following semitattices by symbols:
a)

b)


c)


d)


e) 





f)





g)






Figure 5. Diagram of all XI-subsemilattices of D.
h)





Note that the semilattices in Figure 5 are all XI-semilattices (see [1] and Lemma 1.2.3).
Definition 9. Let us assume that by the symbol 

Further, let 







By the symbol 



Let D' be an XI-subsemilattice of the semilattice D. By 

where
Lemma 4. If X is a finite set, then the following equalities hold
a)
b)
c)
d)
e)
f)
g)
h)
Proof. This lemma immediately follows from Theorem 13.1.2, 13.3.2, and 13.7.2 of the [1] .
Theorem 10. Let 




a)

b)





c)



tisfies the conditions:



d)












e)











f)










g)














h)











Proof. By Lemma 3 we know that 1 to 8 are an XI-semilattices. We prove only statement g. Indeed, if

where


By statement a of the Theorem 6.2.1 (see [1] ) we have:

Further, one can see, that the equalities are true:
We have the elements Z6, T, T' are nonlimiting elements of the sets


By statement b of the Theorem 6.2.1 [1] it follows, that the conditions


Lemma 5. Let 



Lemma 6. Let 


Lemma 7. Let 


Lemma 8. Let 


Lemma 9. Let 


Lemma 10. Let 


Lemma 11. Let 


Lemma 12. Let 


Figure 6 shows all XI-subsemilattices with six elements.
Figure 6. Diagram of all subsemilattices which are isomorphic.
Theorem 11. Let




Example 12. Let
Then









We have









3. Results
Lemma 13. Let 


1)
(see diagram 1 of the Figure 2);
2)
(see diagram 2 of the Figure 2);
3)
(see diagram 3 of the Figure 2);
4)
(see diagram 4 of the Figure 2);
5)
(see diagram 5 of the Figure 2);
6)
(see diagram 6 of the Figure 2);
7)
(see diagram 7 of the Figure 2);
8)
(see diagram 8 of the Figure 2);
Theorem 13. Let





a)
b)




c)



conditions:


d)










e)









f)










g)













h)












Lemma 14. Let 


Lemma 15. Let 


Lemma 16. Let 


Lemma 17. Let 


Lemma 18. Let 


Lemma 19. Let 


Lemma 20. Let 


Lemma 21. Let 


Theorem 14. Let


the semigroup

Example 15. Let

Then



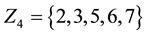





We have









It was seen in ([4] , Theorem 2) that if 







References
- Diasamidze, Ya. and Makharadze, Sh. (2013) Complete Semigroups of Binary Relations. Monograph. Kriter, Turkey, 620 p.
- Diasamidze, Ya. and Makharadze, Sh. (2010) Complete Semigroups of Binary Relations. Monograph. M., Sputnik+, 657 p. (In Russian)
- Diasamidze, Ya., Makharadze, Sh. and Diasamidze, Il. (2008) Idempotents and Regular Elements of Complete Semigroups of Binary Relations. Journal of Mathematical Sciences, Plenum Publ. Cor., New York, 153, 481-499.
- Diasamidze, Ya. and Bakuridze, Al. (to appear) On Some Properties of Regular Elements of Complete Semigroups Defined by Semilattices of the Class
.>http://html.scirp.org/file/6-7402521x653.png" class="200" />.


































































































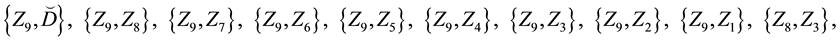



































































































 .>http://html.scirp.org/file/6-7402521x653.png" class="200" />.
.>http://html.scirp.org/file/6-7402521x653.png" class="200" />.