Applied Mathematics
Vol.05 No.18(2014), Article ID:51101,8 pages
10.4236/am.2014.518276
Bell Correlations without Entanglement: A Local Wave Model using Gaussian-Poisson Statistics and Single Count-Pair Selection
Louis Sica1,2
1Institute for Quantum Studies, Chapman University, Orange, CA & Burtonsville, MD, USA
2Inspire Institute Inc., Alexandria, VA, USA
Email: lousica@jhu.edu
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 29 July 2014; revised 29 August 2014; accepted 15 September 2014
ABSTRACT
Based on the violation of Bell inequalities, it has been believed that the derivation of Bell correlations requires a quantum description that depends on entanglement. However, the present paper computes Bell correlations among polarization analyzer output intensities from two spatially separated sets of superposed random wave pairs. To obtain proper Bell correlations, the general statistics must be modified to represent single event pair selection. The correlations between analyzer output components are then in one-to-one correspondence with those computed from the entanglement formalism.
Keywords:
Bell Correlation, Bell Theorem, Locality, Nonlocality, Entanglement

1. Introduction
The Bell theorem and experimental violation of Bell’s inequalities are believed to make the description of Bell correlations impossible without the use of entanglement. If valid, this view would rule out the possibility of local descriptions of these correlations. However, it is shown in [1] and references therein that conclusions based on the Bell theorem as historically reasoned may not be logically drawn. Thus, it becomes appropriate to investigate possible alternatives to quantum descriptions that are widely believed to imply nonlocality.
Below, it is shown that properly normalized covariances resulting from a statistical model of local “twin beams” from a down converter (see Figure 1) exhibit a one-to-one correspondence with Bell correlations. The experimental selection of single photon pairs from the down-converter source, and imposition of quan-
Figure 1. Output of a spontaneous parametric down-converter (SPDC) in type II configuration. Light from the overlap regions of two light-cones constitutes Beams 1 and 2 as used in Bell experiments. Photons are produced in pairs on opposite sides of the arrow with one photon having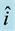 , and the other
, and the other  polarization. In the overlap regions of Beams 1 and 2, each polarization occurs with equal probability, with the two members of a pair having opposite polarization. Correlations of output counts from polarization analyzers (not shown) placed down-beam in each of Beams 1 and 2 are used to measure Bell correlations.
polarization. In the overlap regions of Beams 1 and 2, each polarization occurs with equal probability, with the two members of a pair having opposite polarization. Correlations of output counts from polarization analyzers (not shown) placed down-beam in each of Beams 1 and 2 are used to measure Bell correlations.
tum source boundary conditions, result in modification of a general wave stochastic model to produce results in agreement with the entanglement description.
In Section 2 below, the correlation of polarization analyzer intensity outputs is first derived from the superpositions of orthogonally polarized light wave output from a type II down-converter as used in Bell experiments (see Figure 1). The correlation has the same form as a Bell correlation but is derived from continuous wave variables rather than individual photon-pair events. In Section 3, a semi-classical assumption is introduced: wave intensity is defined to be a statistic representing temporal count density. The two equal source output intensities become Poisson parameters for corresponding count-pair processes. When single count pairs are selected (per detector time constant) from the multiple possible analyzer output pairs, the resulting modified correlations become equal to those given by the quantum entanglement description. However, the process does not imply non- locality, since it results from pairs of equal input intensities and associated twin counts originating in one local spatial region, i.e., the correlations result from common initial conditions imposed on each of two subsequently separated twin beams.
The formalism uses statistical assumptions common in the description of chaotic optical waves [2] . It does not specify a mechanism for the association of photon counts with such waves. Imposition of count-pair statistics as a source boundary condition at rotation angles equal to zero results in Bell correlations at non-zero rotation angles due to random wave interference.
The overall model may be thought of as a generalization of wave particle duality. In two-slit interference, discrete entities assumed to be emanating from a source are manifested as discrete counts at a detector but exhibit the intervening effects of wave interference. In the model below, pairs of counts at initial analyzer angles equal to zero are inserted into, and determine, the statistical parameters of a wave system that determines the count correlations at non-zero analyzer angles.
2. Random wave Description Based on type II down-converter Outputs
Based on the geometry of parametric down converter sources for Bell correlation experiments (see Figure 1) [3] , two complex amplitudes  and
and  are introduced corresponding to superpositions of orthogonally polarized light amplitudes in regions denoted as Beams 1 and 2 of the figure.
are introduced corresponding to superpositions of orthogonally polarized light amplitudes in regions denoted as Beams 1 and 2 of the figure. 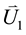 and
and 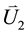 are superpositions of random waves:
are superpositions of random waves:
 (2.1)
(2.1)
and
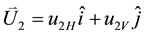 . (2.2)
. (2.2)
In these equations, horizontal and vertical polarization components are indicated by subscripts  and
and  respectively, with
respectively, with 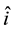 and
and 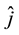 indicating unit vectors along the
indicating unit vectors along the  and
and  axes. The regions of
axes. The regions of  and
and 





The action of polarization analyzers placed in each of Beams 1 and 2 is now described. These transmit and reflect components of 





From these, and 


Thus, two polarized output amplitudes from each input beam occur in directions determined by the rotation angle of the analyzers.
The intensities of the analyzer output components 




where, for example,
yields analyzer 1 outputs

and

where 







and

To proceed, further conditions on the parameters in Equations (2.6)-(2.9) must be specified. First, imposing source characteristics used in Bell experiments [3] requires that

This is implied by the fact that photons are produced in pairs of opposite polarization in Beams 1 and 2. By applying Equations (2.10) to Equations (2.6)-(2.9) it follows that

One concludes that for lossless analyzers, the sum of powers in the output polarizations equals the sum of powers in the input polarizations, which by Equation (2.10) are equal for the two beams.
A phase relation between the input beams must be imposed to make the analysis consistent with requirements of the nonlinear optics process [5] used to produce spontaneous parametric down-conversion (SPDC):

where the

The condition 

When quantities specified in Equations (2.10) and (2.14) are inserted into Equations (2.6)-(2.9), one obtains

Note, if 



with one set rotated 90˚ with respect to the other. The output wave intensities of the analyzers are interchanged due to Equations (2.10) and (2.14).
From Equations (2.15a)-(2.15d), and setting



and

To compute the correlation of 

1) The complex amplitude variables introduced in Equations (2.1) and (2.2) are circular complex Gaussian random variables [7] . They are assumed to be statistically independent but subject to the phase condition introduced in Equation (2.14).
The properties that will be used below follow from assumption 1.
2) From 1, it follows that the wave intensities 

buted. They are assumed to be statistically independent, but they have the same mean
3) The phases are statistically independent of the amplitudes and are uniformly distributed from 


Conditions 1 - 3 are discussed in [2] and [7] , and are commonly used to describe properties of light from thermal sources (and laser speckle patterns). Similar randomness is suggested by photographs of spatial distributions of down converted photons given in [8] .
From points 2 and 3 above, two results are obtained that are used repeatedly in the following. First, if 

Second, a uniform distribution of 



The latter condition plus property 2 applied to Equation (2.15c) implies that

Thus, for Equations (2.15a)-(2.15d),

An important result of this section is now obtained by computing the correlation of 


Using Equations (2.17b) and the independence of the 


while

Inserting the averages of Equations (2.19a) and (2.19b) into Equation (2.18) yields

From the definition of the correlation of any two variables, the correlation of 


The square root variances of 


3. Modification of the Formalism to represent selection ofevent Pairs
In spite of Equation (2.21), correlations among individual pairs of



form that allows interpretation in terms of discrete quantum counts. However, the use of normalized covariances rather than the intensites of Equations (2.15) does result in such a form. It will be shown below that the covariances result from modification of the statistics to represent selection of single event pairs in a detector time-constant (as implemented in experiments), rather than arbitrary numbers of event pairs as implied by the statistics thus far.
The appropriate modifications are obtained by subtracting their common mean value 
tensity components of 


The right-hand side of Equation (3.1) equals that of Equation (2.21), and it appears that nothing has been changed. However, Equation (3.1) may be written as a sum of terms resulting from the contributions of products
such as 


Similarly, the contributions of products 

are given by

However, while Equations (3.2a) and (3.2b) are equal to the corresponding quantum results, it is important to realize that at this point, little discreteness has been introduced into the model.
To achieve a quantum interpretation of Equations (3.1)-(3.2), the continuous variables used are defined in terms of equivalent photon count statistics [2] :
1) Wave intensities are defined as count densities in time.
2) 

cate count pairs as seen by analyzers at
implies that 

3) Experimental parameters and observational protocols are adjusted so that single count pairs are selected as assumed in the entanglement formalism.
To understand the reason for the quantization analysis to be given in Section 3.1, first compute individual averages among the variables of Equations (2.15), 



Using Equations (2.17a) and (2.17b), this becomes

In a similar manner, the other averages may be computed. The relevant averages are


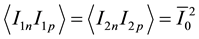
While Equations (3.4a)-(3.4c) suggest Equations (3.2a) and (3.2b) (and quantum mechanical results), they have an additional constant offset, and an amplitude 
Selecting singlephoton pairs from indefinite Numbers of Photon pairs
First, consider Equation (3.4c). To measure correlations at the source, analyzer angles are set to
Writing wave intensities as count averages yields

The 0’s and 1’s in the last two terms are subscripted to indicate to which variable they belong. They represent selected count pair products for which each product equals zero. Note that the values in the right-most double sum occur with low probability, and are deleted under the protocols used in experiments. After averaging over the exponentially distributed variables, the average over the double sum is

Thus, the constant on the right side of Equation (3.4c) corresponds to events that are excluded if single event
pairs are selected from the range of possibilities. Clearly, the situation is the same for
ther, Equation (3.4c) holds for all equal analyzer angles so that the boundary condition at 

From Equations (2.15a)-(2.15d), when




As above, Equation (3.4b) represents observation under the condition of single pair selection if the additive constant 
The same reasoning may be extended to Equation (3.4a). Observe from Equations (2.15) that

Under this condition, Equation (3.4a) reduces to Equation (3.4c):

The end result is that Equations (3.4a)-(3.4c) represent observations under single count pair selection, if 
Similar considerations apply to the interpretation of the multiplicative factor 


where 


The probability product for duplicate photons equals the probability for one photon squared, i.e.

same. Given that the probability of two counts on a side is made small compared to one count,

pendent processes with equal parameters, the second component of Equation (3.4a) yields

Given Equation (2.17a),


It is now necessary to apply the normalization used in the definition of correlation (the denominator of Equation (3.2a) to Equation (3.10), again taking pair selection into account. For beam 1, since 



From count selection at

after ensemble averaging as in Equation (2.19a). Then

with anequalresult for
From Equations (3.10) and (3.11c), one has

with an equal result for
used in experiments, Equation (3.4a) is modified to Equation (3.2a). From the above analysis, the same procedure modifies Equation (3.4b) to Equation (3.2b).
4. Discussion
It has been shown above that the interference of twin pairs of waves yields polarization analyzer intensity outputs whose appropriate cross correlations may be used to compute Bell correlations. The wave statistical parameters used are set equal to the basic observational count parameters found in SPDC. These results depend on interpreting wave intensity variables as counts per unit time and on the experimental restriction of correlations to represent single event pairs. When the general wave optical statistics are adjusted to represent single source-pair selection at analyzer angles equal to zero, the formalism provides the same results as the entanglement formalism at non-zero angles. This is a principle result of this paper.
5. Conclusions
It has been believed that the violation of the Bell inequalities from Bell’s theorem implies that only the formalism of quantum entanglement can describe the observed correlations of Bell experiments. Although it produces the experimentally observed correlations, the entanglement formalism has the troubling implication of non-lo- cality, or what some call “non-reality”. The purpose of the present investigation has been to examine an alternative formulation of the problem that does not have these troubling properties. It is based on the superposition of duplicate pairs of orthogonally polarized waves that, due to quantum source boundary conditions, produce “twin” count pairs and hence “twin” wave intensity pairs. Non-locality does not appear to be a consequence of the formalism. Results of measurements on the spatially separated beams are correlated due to the duplicate wave intensities and counts.
No hidden variables have been used in the calculation. The wave optics formalism and assumed statistics for describing correlations among twin beam polarization components depend on empirical results. These lead to the following assumptions: 1) intensities are defined as counts/time; 2) counts are not divided at polarization analyzers; and 3) photons are created in duplicate at the source, with the two members of each source pair having opposite polarization. Condition 3) provides initial conditions for the physical processes that follow in each down-converter beam. The fact that photons occur in duplicate does not in itself imply nonlocality, since initially, in the down-converter crystal where the photons are created, the output waves are superimposed.
The formalism is silent on the question of the connection of photons to waves other than through the usual intensity definition of count rate. Thus, one obtains a statistical description in both the semi-classical wave optics picture presented, and the quantum entanglement picture.
The possibility of an alternative to the entanglement description has been thought to be ruled out by violation of Bell’s inequalities. However, the Bell theorem is fundamentally flawed, as shown in [1] and references therein, so it may no longer be used ab initio to deny efforts to construct alternative descriptions of these phenomena.
Some of the analyses given in the present paper were described in a preliminary (unpublished) form in [9] .
Acknowledgements
The author is grateful to Armen Gulian, and Joe G. Foreman of Chapman University, Burtonsville, MD. for stimulating discussions, and especially to Joe G. Foreman for critiques of the presentation.
Cite this paper
LouisSica,11, (2014) Bell Correlations without Entanglement: A Local Wave Model Using Gaussian-Poisson Statistics and Single Count-Pair Selection. Applied Mathematics,05,2899-2907. doi: 10.4236/am.2014.518276
References
- 1. Sica, L. (2013) Logical Difficulty from Combining Counterfactuals in the GHZ-Bell Theorems. Applied Mathematics, 4, 90-94,
http://dx.doi.org/10.4236/am.2013.410A3012 - 2. Loudon, R. (2000) The Quantum Theory of Light. 3rd Editon, Oxford University Press, New York, 276.
- 3. Kwiat, P.G., Mattle, K., Weinfurter, H., Zeilinger, A., Sergienko, A.V. and Shih, Y. (1995) New High-Intensity Source of Polarization-Entangled Photon Pairs. Physical Review Letters, 75, 4337-4342.
http://dx.doi.org/10.1103/PhysRevLett.75.4337 - 4. Goodman, J.W. (2005) Introduction to Fourier Optics. 3rd Edition, Roberts & Company Publishers, Greenwoood Village, Co., 38.
- 5. Smith, R.G. (1970) Effects of Momentum Mismatch on Parametric Gain. Journal of Applied Physics, 41, 4121-4124.
http://dx.doi.org/10.1063/1.1658422 - 6. Waks, E., Sanders, B.C., Diamanti, E. and Yamamoto, Y. (2006) Highly Nonclassical Photon Statistics in Parametric Down Conversion. Physical Review A, 73, Article ID: 033814.
- 7. Goodman, J.W. (1984) Statistical Properties of Laser Speckle Patternsin Laser Speckle and Related Phenomena. In: Dainty, J.C., Ed., Topics in Applied Physics, 2nd Edition, Springer-Verlag, Berlin, 9-75.
- 8. Lugiato, L.A., Gatti, A. and Brambilla, E. (2002) Quantum Imaging. Journal of Optics B Quantum and Semiclassical Optics, 4, 176.
- 9. Sica, L. (2011) Local Probability Model for the Bell Correlation based on the Statistics of Chaotic Light and Non-Commutative Processes. (Unpublished).
http://arxiv.org/pdf/1106.1453v1.pdf .


