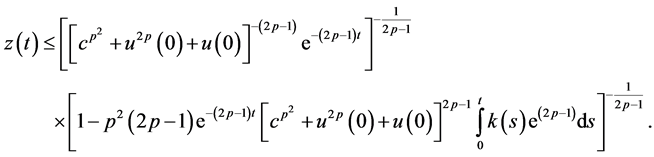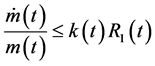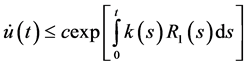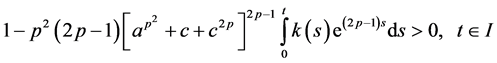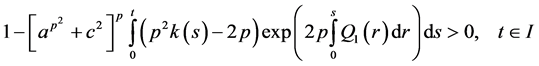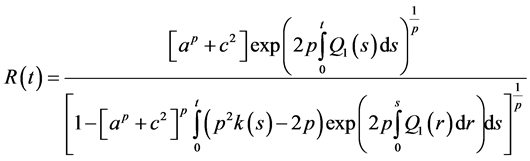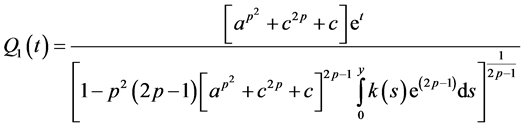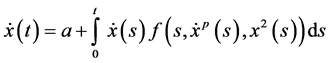Received 6 September 2014; revised 8 October 2014; accepted 18 October 2014

ABSTRACT

The aim of this present paper is to establish some new integrodifferential inequalities of Gronwall type involving functions of one independent variable which provide explicit bounds on unknown functions. The inequalities given here can be used in the analysis of a class of differential equations as handy tools.

Keywords:

Integral Inequalities, Two Independent Variables, Nondecreasing, Nonincreasing

1. Introduction

The differential and integral inequalities occupy a very privileged position in the theory of differential and integral equations. In recent years, these inequalities have been greatly enriched by the recognition of their potential and intrinsic worth in many applications of the applied sciences. The integrodifferential inequalities recently established by Gronwall and others [1] -[12] have attracted considerable attention in the theory of differential and integral equations. This fact encourages us to find the explicit bounds on some fundamental integrodifferential inequalities which can be applied fairly well to achieve a diversity of desired goals. In [3] , Pachpatte (1977) gave the following useful integrodifferential inequality:

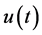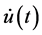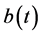Let, and be nonnegative continuous functions defined on and 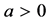is constant. If

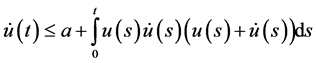(1.1)

for and 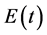is defined by

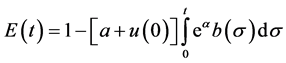
then

for 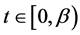where

.

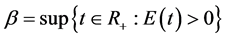Our goal in this paper is to establish new explicit bounds on some basic integrodifferential inequalities of one independent variable which will be equally important in handling the inequality (1.1). Given application in this paper also illustrates the usefulness of our result.

2. Main Results

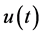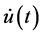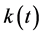Theorem 2.1: Let, and be nonnegative continuous functions defined on 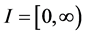for which the inequality

(2.1)

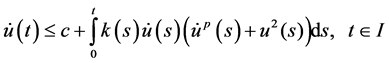
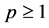
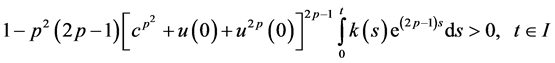
holds, where is positive constant and. If

(2.2)

and

(2.3)

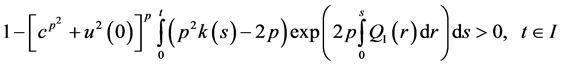
then

, (2.4)

, and

(2.5)

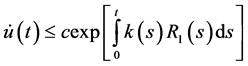
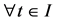
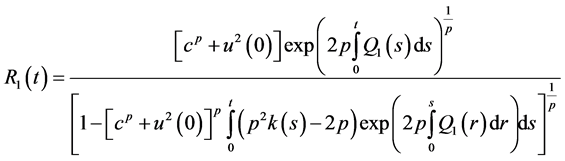
also

(2.6)

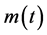
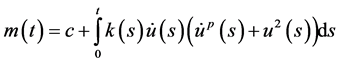
Proof: Define a function by the right-hand side of (2.1). Then

(2.7)

where

(2.8)

Then from (2.1) and (2.7), we have

(2.9)

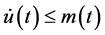
Integrating both sides of (2.9) from 0 to t, we observe that

(2.10)

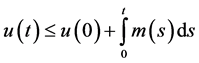
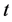
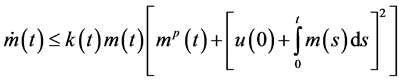
Differentiating both sides of (2.7) with respect to and using (2.9) and (2.10), we get

(2.11)

Define a function by the right-hand side of (2.11), then

(2.12)

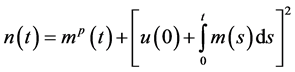
where

(2.13)

It is clear that

(2.14)

By using (2.12) in (2.11), we have

(2.15)

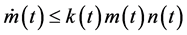
Differentiating both sides of (2.12) with respect to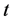, we get

By using (2.14) and (2.15) in the above equation, we observe that

(2.16)

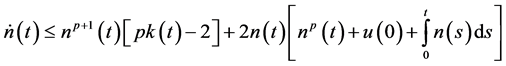
Let

(2.17)

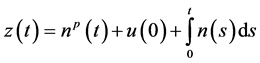
where

(2.18)

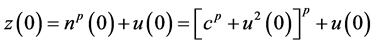
and

(2.19)

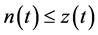
Using (2.17) in (2.16), we get

(2.20)

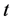
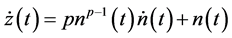
Differentiating both sides of (2.17) with respect to, we get

(2.21)

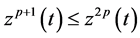
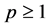
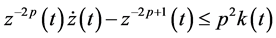
Inequality (2.21) by using (2.19) and (2.20), and since if takes the form

(2.22)

Let

(2.23)

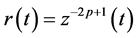
where

(2.24)

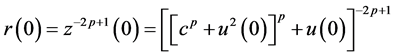
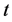
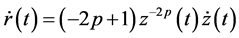
Differentiating both sides of (2.23) with respect to, we get

(2.25)

Inequality (2.22) by using (2.23) and (2.25), takes the form

(2.26)

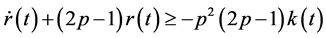
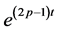
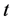
Multiplying both sides of (2.26) by and integrating the resulting inequality from 0 to, and using (2.24), we have

By using (2.23) in the above inequality, it can be seen that

which can be rewritten as

(2.27)

Using (2.27) in (2.20), we observe that

(2.28)

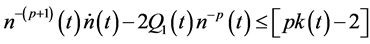
Let

(2.29)

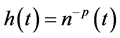
where

(2.30)

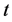
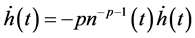
Differentiating both sides of (2.29) with respect to, we get

(2.31)

Inequality (2.28) by using (2.29) and (2.31), takes the form

(2.32)

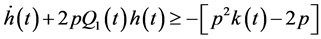
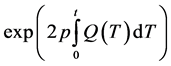
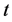
Multiplying both sides of (2.32) by and integrating the resulting inequality from 0 to, and using (2.29) and (2.30), we have

which can be rewritten as

(2.33)

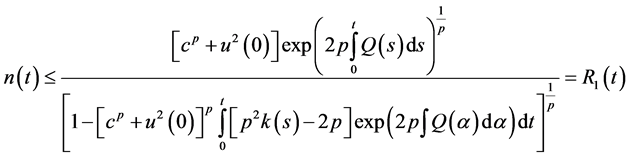
From (2.15) and (2.33), we get

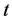
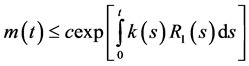
Integrating both sides of the above inequality from 0 to, and from (2.8), we observe that

(2.34)

From (2.9) and (2.34), we have

Application: As an application we obtain the bound on the solution of the differential equation of the formulation of the form

(2.35)

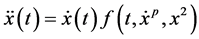
with the given initial conditions

(2.36)

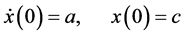
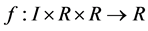
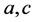
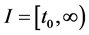
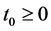
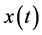
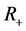
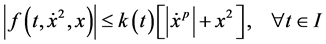
where is a continuous function and are real constants.,. Here we assume that the solution of (2.35) and (2.36) exists on Assume that the function in (2.35) satisfies the condition

(2.37)

where 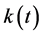is a real valued nonnegative continuous function defined on. If

and

then the bounds on the solution (2.35) takes the form

(2.38)

, where, , and

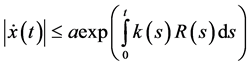
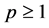
Also

Proof: Integrating both sides of (2.35) from 0 to, and using (2.36), we observe that

Taking absolute values of both sides of the above equation and using (2.37), we get

(2.39)

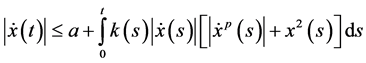
The remaining proof is the same as Theorem 2.1 by following the same steps from (2.7)-(2.35) in (2.39) with suitable modifications, we get the required bound of (2.35).

We note that many generalizations, extensions, variants and applications of the inequality given in this paper are possible and we hope that the result given here will assure greater importance in near future.

References