Applied Mathematics
Vol.5 No.13(2014), Article
ID:47626,9
pages
DOI:10.4236/am.2014.513183
Block Matrix Representation of a Graph Manifold Linking Matrix Using Continued Fractions
Fernando I. Becerra López, Vladimir N. Efremov, Alfonso M. Hernandez Magdaleno
Mathematics Department, CUCEI, University of Guadalajara, Guadalajara, Mexico
Email: mail@ferdx.com, efremov@cencar.udg.mx, 137mag@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 19 April 2014; revised 27 May 2014; accepted 6 June 2014
ABSTRACT
We consider the block matrices and 3-dimensional graph manifolds associated with a special type of tree graphs. We demonstrate that the linking matrices of these graph manifolds coincide with the reduced matrices obtained from the Laplacian block matrices by means of Gauss partial diagonalization procedure described explicitly by W. Neumann. The linking matrix is an important topological invariant of a graph manifold which is possible to interpret as a matrix of coupling constants of gauge interaction in Kaluza-Klein approach, where 3-dimensional graph manifold plays the role of internal space in topological 7-dimensional BF theory. The Gauss-Neumann method gives us a simple algorithm to calculate the linking matrices of graph manifolds and thus the coupling constants matrices.
Keywords:Graph Manifolds, Continued Fractions, Laplacian Matrices, Kaluza-Klein

1. Introduction
Graphs can serve as a universal remedy for the codification and classification of topological spaces, matrices, dynamical systems, etc. In this article, we consider the following question: how the topological invariants of manifold corresponding to a tree graph (graph manifold) can be calculated using the method of Gauss-Neumann partial diagonalization of Laplacian matrix defined for the same graph. This calculation can be useful in multidimensional models of Kaluza-Klein type, where coupling constants of gauge interactions are simulated by the rational linking matrices of the internal space [1] . We constructed various models [2] [3] where the role of internal spaces is played by a specific family of 3-dimensional graph manifolds, whose rational linking matrices describe the hierarchy of gauge coupling constants of the real universe. The basic structure blocks of these graph manifolds are Seifert fibered Brieskorn homology spheres, defined as the link of Brieskorn singularity
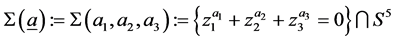 , with
, with 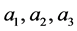 pairwise relatively prime positive numbers [4] . Bh-spheres belong to the class of Seifert fibered homology spheres (Sfh-spheres). On each of these manifolds, there exists a Seifert fibration with unnormalized Seifert invariants
pairwise relatively prime positive numbers [4] . Bh-spheres belong to the class of Seifert fibered homology spheres (Sfh-spheres). On each of these manifolds, there exists a Seifert fibration with unnormalized Seifert invariants  subject to
subject to 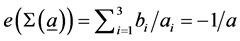 , where
, where 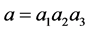 and
and 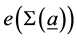 is its rational Euler number, the well known topological invariant of a Bh-sphere. The topological operation known as plumbing [5] is used to past together Bh-spheres according to plumbing diagrams (Figure 4) which can be transformed in plumbing graphs (Figure 3). This type of graphs and their Laplacian block matrices is the main object of attention in this article.
is its rational Euler number, the well known topological invariant of a Bh-sphere. The topological operation known as plumbing [5] is used to past together Bh-spheres according to plumbing diagrams (Figure 4) which can be transformed in plumbing graphs (Figure 3). This type of graphs and their Laplacian block matrices is the main object of attention in this article.
The paper is organized as follows. In section 2 we define the type of tree graphs considered in this paper (plumbing graphs) and Laplacian matrices for these plumbing graphs. We recall also the Gauss-Neumann method of partial diagonalization by means of which we obtain the reduced rational tridiagonal matrix for each plumbing graph. In section 3 we construct graph manifolds codified by the plumbing graphs defined in section 2 and calculate the main topological invariant for these 3-dimensional manifolds, namely rational linking matrix. Then we demonstrate that the linking matrices of these graph manifolds coincide with the reduced matrices obtained from the Laplacian block matrices by means of Gauss-Neumann partial diagonalization procedure. Finally, we conclude formulating our main results and considering an example of their application for the topological field theory.
2. Block Matrix Representation for a Graph  of Tree Type
of Tree Type
We begin from the definition of graph  as a finite one-dimensional simplicial complex, which does not contain multiple edges and loops, i.e. we consider only the graph of tree type. An integer weight
as a finite one-dimensional simplicial complex, which does not contain multiple edges and loops, i.e. we consider only the graph of tree type. An integer weight 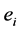 is assigned to each vertex of
is assigned to each vertex of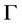 . Vertices with at least three edges are called nodes. For simplicity we shall use graphs with nodes of minimal valence (n = 3) only (a generalization to
. Vertices with at least three edges are called nodes. For simplicity we shall use graphs with nodes of minimal valence (n = 3) only (a generalization to 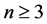 is obvious). Suppose that the set of nodes
is obvious). Suppose that the set of nodes 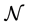 of the graph
of the graph 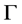 is non-empty. Considering the graph
is non-empty. Considering the graph 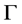 as a one-dimensional simplicial complex, we take the complement
as a one-dimensional simplicial complex, we take the complement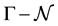 . This complement is the disjoint union of straight line segments which are the maximal chains of
. This complement is the disjoint union of straight line segments which are the maximal chains of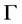 . Figure 1 shows a maximal internal chain
. Figure 1 shows a maximal internal chain 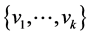 of length k between two nodes
of length k between two nodes 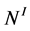 and
and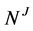 , with weights
, with weights 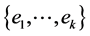 embedded in a tree graph
embedded in a tree graph . The chain is maximal because it cannot be included in some larger chain. Figure 2 shows a maximal terminal chain
. The chain is maximal because it cannot be included in some larger chain. Figure 2 shows a maximal terminal chain 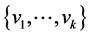 of length k also with weights
of length k also with weights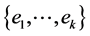 .
.
In this paper we shall considered only the simplest type of graphs which are called plumbing graphs. An example of plumbing graph 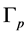 is given in Figure 3. This type of graphs is used to codify the plumbing graph manifolds [5] which will be constructed in the following section, where it will be clear why weights of plumbing graph are called Euler numbers. In Figure 3 the Euler numbers
is given in Figure 3. This type of graphs is used to codify the plumbing graph manifolds [5] which will be constructed in the following section, where it will be clear why weights of plumbing graph are called Euler numbers. In Figure 3 the Euler numbers 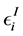 and
and 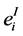 decorate the vertices with valence 1 and 2. The nodes are marked by NI with
decorate the vertices with valence 1 and 2. The nodes are marked by NI with  and form a straight line or chain structure. We associate
and form a straight line or chain structure. We associate

Figure 1. A maximal internal chain of length k.

Figure 2. A maximal terminal chain of length k.

Figure 3. The plumbing graph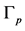 .
.
to each node a weight equal to zero that is connected with using of the unnormalized Seifert invariants for Bh-spheres, which are the block elements for the construction of graph manifolds [6] .
Now let’s define a Laplacian matrix for the plumbing graph 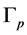 as follows:
as follows:
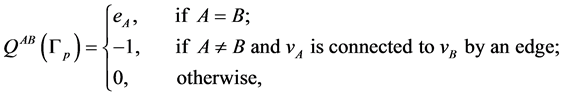
with integer numbers 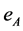 corresponding to each vertex
corresponding to each vertex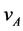 . This is a tridiagonal block matrix containing all the information about the graph
. This is a tridiagonal block matrix containing all the information about the graph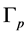 . The I-th fragment of the matrix
. The I-th fragment of the matrix 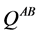 which corresponds to the I-th piece of the graph
which corresponds to the I-th piece of the graph 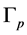 shown in Figure 3 is represented as
shown in Figure 3 is represented as
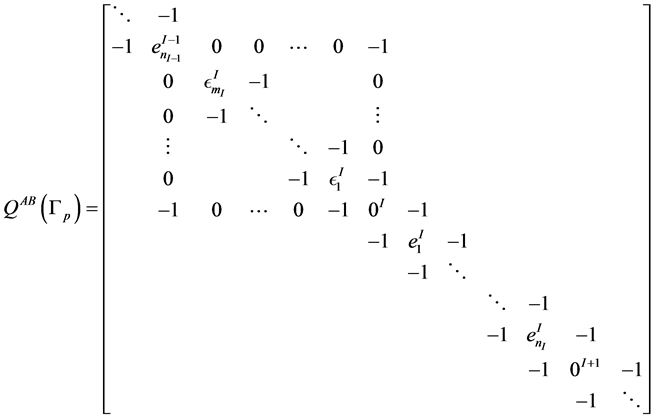
Note that 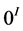 denotes an integer number 0 corresponding to the node
denotes an integer number 0 corresponding to the node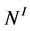 . Now we pay attention to the tridiagonal submatrices (blocks) of type
. Now we pay attention to the tridiagonal submatrices (blocks) of type

and notice that using Gauss-Neumann partial diagonalization [7] the matrix is equivalent to the rational block matrix
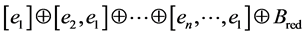
where
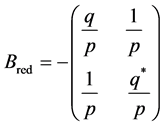
and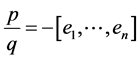 ,
,  ,
,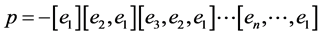 . Here we are using the standard definition of continued fraction
. Here we are using the standard definition of continued fraction
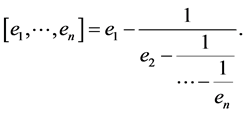
Applying the general Gauss-Neumann partial diagonalization method for the matrix 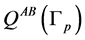 we obtain a similar result where
we obtain a similar result where 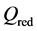 is a rational tridiagonal matrix of rank
is a rational tridiagonal matrix of rank 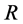 (the number of nodes of the graph
(the number of nodes of the graph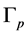 ) whose elements on the diagonal are a sum of three terms representing each maximal chain connecting to the node.
) whose elements on the diagonal are a sum of three terms representing each maximal chain connecting to the node.
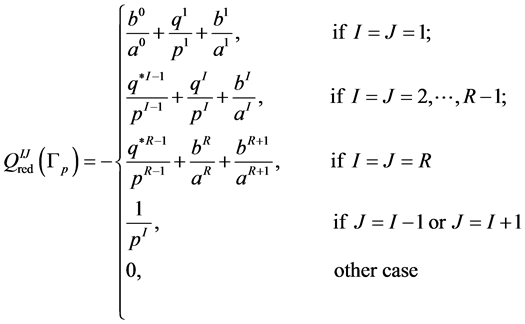 (1)
(1)
where 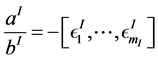 are continued fractions for a terminal chain, and
are continued fractions for a terminal chain, and 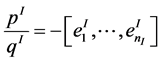 for a internal chain. We have used the notation
for a internal chain. We have used the notation 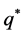 to indicate that the order of the numbers on the continued fraction is inverse, i.e.
to indicate that the order of the numbers on the continued fraction is inverse, i.e.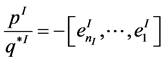 . So, we can reduce each chain of
. So, we can reduce each chain of 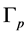 to a rational number
to a rational number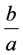 ,
, 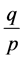 or
or 
which is represented as a continued fraction, and thus reduce the original block tridiagonal matrix 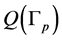 to a tridiagonal matrix
to a tridiagonal matrix  whose size depends just of the number of nodes of
whose size depends just of the number of nodes of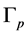 . It is important to note that it is possible to obtain the original matrix
. It is important to note that it is possible to obtain the original matrix 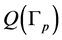 from the reduced matrix
from the reduced matrix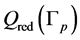 .
.
3. Rational Linking Matrix for Graph Manifold 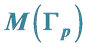
In this section we will construct a plumbing graph manifold 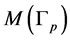 codified by the same graph
codified by the same graph 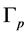 as in section 2. Now we see the weight
as in section 2. Now we see the weight 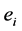 as the Euler number of the principal S1-(U(1)-)bundle, corresponding to i-th vertex
as the Euler number of the principal S1-(U(1)-)bundle, corresponding to i-th vertex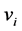 . We define the bundle
. We define the bundle 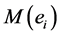 associated to each vertex
associated to each vertex 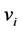 as S1-bundle over
as S1-bundle over 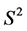 with the Euler number
with the Euler number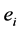 , which can be pasted together from two trivial bundles over
, which can be pasted together from two trivial bundles over  as follows [8] [9]
as follows [8] [9]

where
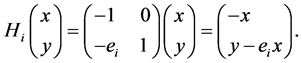
Note that the above is a well known description of the lens space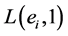 , so the total space of the bundle is
, so the total space of the bundle is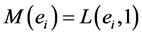 . To perform pasting operation, which is known as plumbing between the S1-bundles, we must use the trivial bundles over annuli
. To perform pasting operation, which is known as plumbing between the S1-bundles, we must use the trivial bundles over annuli 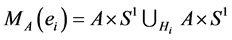 where A is an annulus or twice punctured sphere
where A is an annulus or twice punctured sphere . The manifold
. The manifold 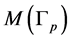 is pasted together from the manifolds
is pasted together from the manifolds 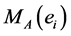 as follows [9] : whenever vertices
as follows [9] : whenever vertices  and
and  are connected by an edge
are connected by an edge 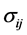 in
in  we paste a boundary component
we paste a boundary component 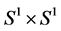 of
of 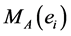
to a boundary component 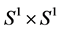 of
of 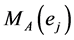 by the map
by the map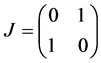 :
:
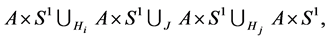 so the base and fiber coordinates are exchanged under the plumbing operation. Thus the edge
so the base and fiber coordinates are exchanged under the plumbing operation. Thus the edge 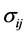 corresponds to the torus
corresponds to the torus 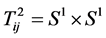 along which the pieces
along which the pieces  and
and 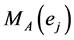 pasted together.
pasted together.
For example, the plumbing of the chain shown in Figure 1 gives us the pasting
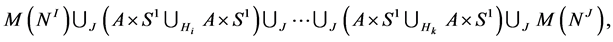
where 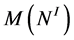 is a
is a 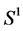 -bundle associating with the node
-bundle associating with the node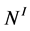 . This chain corresponds to a Seifert fibered thick torus (homeomorphic to
. This chain corresponds to a Seifert fibered thick torus (homeomorphic to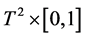 ) in graph manifold
) in graph manifold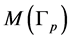 . Also, the terminal maximal chain shown in Figure 2 corresponds to a Seifert fibered solid torus (homeomorphic to
. Also, the terminal maximal chain shown in Figure 2 corresponds to a Seifert fibered solid torus (homeomorphic to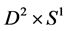 ) in
) in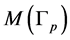 . The using of graphs with nodes of valence
. The using of graphs with nodes of valence 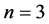 (as in Section 2) corresponds to plumbing of Brieskorn homology spheres (Bh-spheres) [4] .
(as in Section 2) corresponds to plumbing of Brieskorn homology spheres (Bh-spheres) [4] .
Now recall that each edge 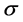 of
of 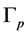 relates to the embedded torus
relates to the embedded torus 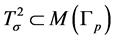 and the collection of all these tori cuts the graph manifold
and the collection of all these tori cuts the graph manifold 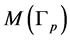 into disjoint union of circle bundles over n times punctured sphere
into disjoint union of circle bundles over n times punctured sphere 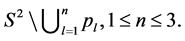 In general, the bundles are over compact surfaces of genus g with some boundary components, see [8] [9] . Such a collection of tori
In general, the bundles are over compact surfaces of genus g with some boundary components, see [8] [9] . Such a collection of tori  is called a graph structure on
is called a graph structure on 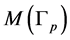 by Waldhausen [10] . We want to define the Jaco-Shalen-Johannson (JSJ) graph structure
by Waldhausen [10] . We want to define the Jaco-Shalen-Johannson (JSJ) graph structure  of the Waldhausen graph structure and to specify the corresponding JSJ-decomposition of graph manifold
of the Waldhausen graph structure and to specify the corresponding JSJ-decomposition of graph manifold 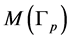 on the set of Seifert fibered pieces
on the set of Seifert fibered pieces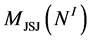 . Let us denote
. Let us denote 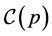 the set of maximal chains in the graph
the set of maximal chains in the graph . This set can be written as a disjoint union
. This set can be written as a disjoint union 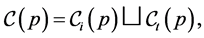 where
where 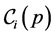 denote the set of interior chains and
denote the set of interior chains and 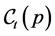 is the set of terminal chains. The edges of
is the set of terminal chains. The edges of 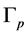 contained in a chain
contained in a chain 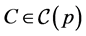 correspond to a set of parallel tori in
correspond to a set of parallel tori in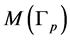 . Choose one torus
. Choose one torus 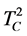 among them and define
among them and define
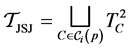 (2)
(2)
This set of tori performs the well known JSJ-decomposition of the graph manifold  [11] .
[11] .
By construction, each piece 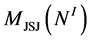 (denoted as
(denoted as 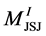 for brevity) of JSJ-decomposition that corresponds to the node
for brevity) of JSJ-decomposition that corresponds to the node 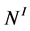 contains a unique piece
contains a unique piece 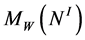 (which we shall denote as
(which we shall denote as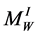 ) of Waldhausen decomposition associated with the same node
) of Waldhausen decomposition associated with the same node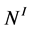 . One can extend in a unique way up to isotopy the natural Seifert structure without exceptional fibers on
. One can extend in a unique way up to isotopy the natural Seifert structure without exceptional fibers on 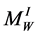 to a Seifert fibration on
to a Seifert fibration on 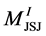 with exceptional fibers. Thus in these terms the JSJ-decomposition of the manifold
with exceptional fibers. Thus in these terms the JSJ-decomposition of the manifold 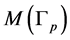 is defined completely by
is defined completely by 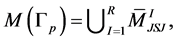 where R is the number of nodes in
where R is the number of nodes in 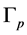 and the bar over M means the closure of the piece
and the bar over M means the closure of the piece .
.
Note that there exists an uncertainty in the choice of the torus  for each internal chain which appear in the JSJ-structure (2). We can remove this uncertainty in following way. Let us perform the maximal extension of the natural Seifert fibration from each
for each internal chain which appear in the JSJ-structure (2). We can remove this uncertainty in following way. Let us perform the maximal extension of the natural Seifert fibration from each  and denote the obtained Seifert fibered piece of
and denote the obtained Seifert fibered piece of  by
by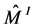 . It is clear that
. It is clear that 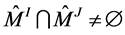 if and only if there exists a chain
if and only if there exists a chain 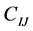 joining the nodes
joining the nodes 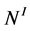 and
and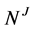 . If we start with plumbing of R Bh-spheres
. If we start with plumbing of R Bh-spheres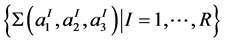 , the resulting graph three-manifold will be integer homology sphere [4] [9] (
, the resulting graph three-manifold will be integer homology sphere [4] [9] (![]() -homology sphere), which in general case does not have the global Seifert fibration. But we can construct the JSJ-covering
-homology sphere), which in general case does not have the global Seifert fibration. But we can construct the JSJ-covering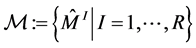 , such as each
, such as each 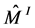 is a Seifert fibered space and it is maximal in the sense described above.
is a Seifert fibered space and it is maximal in the sense described above.
Suppose that we perform the plumbing operation according to the plumbing diagram , shown on the Figure 4. Thus our plumbing diagrams will always have the pairwise coprime weights around each node and correspond to
, shown on the Figure 4. Thus our plumbing diagrams will always have the pairwise coprime weights around each node and correspond to ![]() -homology spheres [5] .
-homology spheres [5] .
We construct the plumbing graph  for a
for a ![]() -homology sphere, following [5] [8] [9] (as a result we shall obtain a graph of type shown in Figure 3). First of all we calculate the characteristics of maximal chains. For terminal chains the integer Euler numbers
-homology sphere, following [5] [8] [9] (as a result we shall obtain a graph of type shown in Figure 3). First of all we calculate the characteristics of maximal chains. For terminal chains the integer Euler numbers 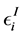 are defined by the continued fraction:
are defined by the continued fraction:
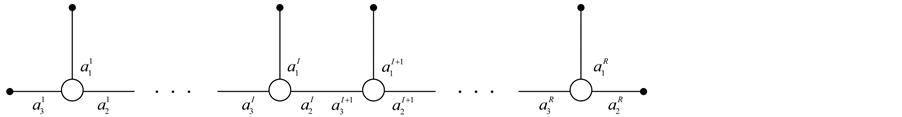
Figure 4. A plumbing (splicing) diagram Δp.
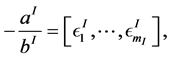 (3)
(3)
where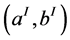 ,
, 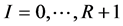 are the Seifert invariants, numerated in the following way
are the Seifert invariants, numerated in the following way
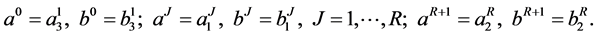 (4)
(4)
For internal chains the integer Euler numbers  are defined by
are defined by
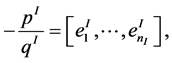 (5)
(5)
where the Seifert (orbital) invariants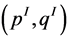 ,
, 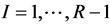 characterize the thick tori
characterize the thick tori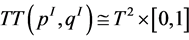 , which are created by the plumbing operations performed between the nodes
, which are created by the plumbing operations performed between the nodes 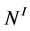 and
and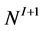 , see [6] [9] . These invariants identify also the extra lens spaces
, see [6] [9] . These invariants identify also the extra lens spaces 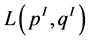 which arise in four-dimensional plumbed V-cobordism (corresponding to the graph
which arise in four-dimensional plumbed V-cobordism (corresponding to the graph ) with
) with

for the ordering fixed by the plumbing diagram in Figure 4. From this representation of the plumbing graph it is clear that for 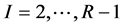 the set
the set 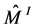 of JSJ-covering
of JSJ-covering 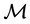 has the form
has the form
 (6)
(6)
where 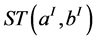 is a Seifert fibered solid torus with Seifert invariants
is a Seifert fibered solid torus with Seifert invariants 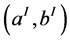 and
and
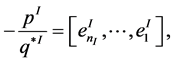 (7)
(7)
For the cases 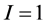 and
and 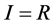 the formulas are different from (6):
the formulas are different from (6):
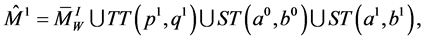 (8)
(8)
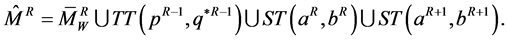 (9)
(9)
Moreover 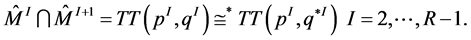 Here the symbol
Here the symbol  indicates that
indicates that  and
and 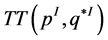 are homeomorphic, but their Seifert structures are characterized by different integer Euler numbers defined by (5) and (7) respectively. Thereby the thick torus between the nodes NI and
are homeomorphic, but their Seifert structures are characterized by different integer Euler numbers defined by (5) and (7) respectively. Thereby the thick torus between the nodes NI and 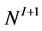 has two Seifert fibrations: the first is the extension of the natural Seifert fibration defined on the piece
has two Seifert fibrations: the first is the extension of the natural Seifert fibration defined on the piece 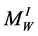 and the second one is obtained as extension from the piece
and the second one is obtained as extension from the piece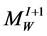 . These Seifert fibrations are connected by the matrix [6] [9] :
. These Seifert fibrations are connected by the matrix [6] [9] :
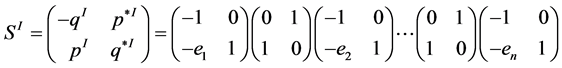
in the following sense. Recall that edges of  contained in a chain
contained in a chain  (between the nodes NI and
(between the nodes NI and ) correspond to the set parallel tori in
) correspond to the set parallel tori in . On any of these tori there exist two bases formed by the section lines and the fibers pertain to the Seifert fibrations extended from
. On any of these tori there exist two bases formed by the section lines and the fibers pertain to the Seifert fibrations extended from 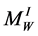 and
and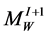 , which we denote as the pair of columns
, which we denote as the pair of columns
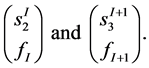 (10)
(10)
Subindices 2 and 3 manifest that 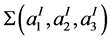 and
and 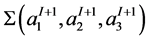 are plumbed together along the singular fibers with Seifert invariants
are plumbed together along the singular fibers with Seifert invariants 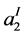 and
and 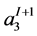 (see Figure 4). Then the transformation between these section-fiber bases is described by
(see Figure 4). Then the transformation between these section-fiber bases is described by

where 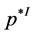 is defined from
is defined from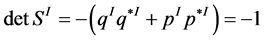 .
.
Now we introduce the one-form bases 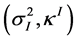 and
and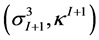 , duals to the bases (10) in the following sense:
, duals to the bases (10) in the following sense:
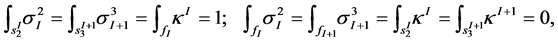
where the integrals are calculated over any such section line or fiber as, for example, in [12] . Thus we obtain the corresponding transformations between the the dual one-forms:
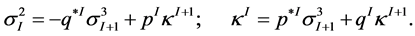 (11)
(11)
We suppose that the forms 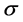 and
and 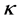 are dual with respect to the bilinear pairing defined as
are dual with respect to the bilinear pairing defined as
 (12)
(12)
Also we shall used the integrals
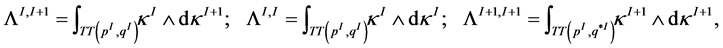
which define the linking (intersection) numbers of the fiber structures  and
and 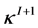 defined on thick torus
defined on thick torus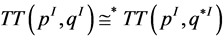 . We can obtain the rational linking matrix for
. We can obtain the rational linking matrix for 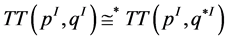 by means of multiplication of the Equations (11) by
by means of multiplication of the Equations (11) by 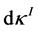 and
and 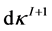 and integration over
and integration over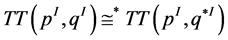 . Applying the duality conditions (12) we obtain:
. Applying the duality conditions (12) we obtain:
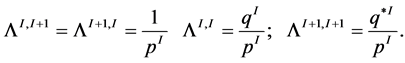 (13)
(13)
The rational numbers 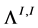 and
and 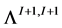 are also known as Chern classes of the line V-bundles associated with the Seifert fibrations with the U(1)-invariant connection forms
are also known as Chern classes of the line V-bundles associated with the Seifert fibrations with the U(1)-invariant connection forms  and
and 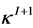 on the lens spaces
on the lens spaces  and
and 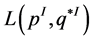 respectively [12] .
respectively [12] .
Now we are ready to calculate the rational linking matrix for the graph manifold  (see Figure 3):
(see Figure 3):
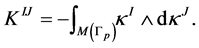
We integrate here over the three dimensional graph manifold 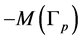 to obtain a positive definite linking matrix. This manifold has the opposite orientation with respect to the graph manifold
to obtain a positive definite linking matrix. This manifold has the opposite orientation with respect to the graph manifold 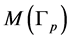 obtained directly by plumbing of Bh-spheres, which are defined as links of singularities. This construction of the graph manifold
obtained directly by plumbing of Bh-spheres, which are defined as links of singularities. This construction of the graph manifold 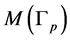 gives the possibility to represent it also as a link of singularity that guarantees its rational linking matrix to be negative definite (for details see [5] ).
gives the possibility to represent it also as a link of singularity that guarantees its rational linking matrix to be negative definite (for details see [5] ).
From the tree structure of the graph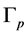 , and from the first equation in (13) we immediately obtain, that for
, and from the first equation in (13) we immediately obtain, that for  the nonzero elements are only
the nonzero elements are only
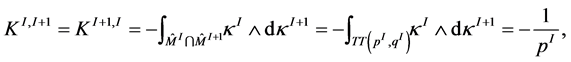
for 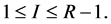
If , we have
, we have
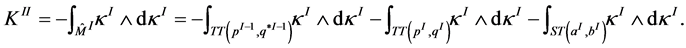
Here we use the decomposition (6) of the piece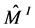 , and that the integral over trivial Seifert fibration
, and that the integral over trivial Seifert fibration 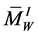 is zero. Then according to the two last equations in (13) we obtain the matrix element
is zero. Then according to the two last equations in (13) we obtain the matrix element
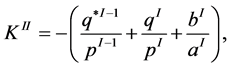 (14)
(14)
also known as the Chern class of line V-bundle associated with the Seifert fibration of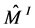 .
.
For 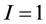 and
and  the matrix elements are
the matrix elements are
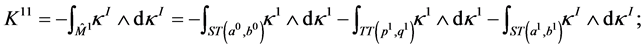 (15)
(15)
 (16)
(16)
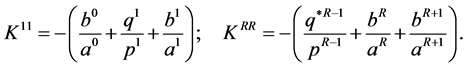 (17)
(17)
Here we have used the decompositions (8) and (9) as well as the notations (4).
4. Conclusions
Comparing the reduced matrix  (1) with the results (14) and (17) for the rational linking matrix K of the graph manifold
(1) with the results (14) and (17) for the rational linking matrix K of the graph manifold  we observe that decomposing the rational invariants into continued fractions according to (3), (5) and (7), we can create the graph
we observe that decomposing the rational invariants into continued fractions according to (3), (5) and (7), we can create the graph 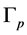 (related to diagram
(related to diagram ) and obtain the rational linking matrix K of
) and obtain the rational linking matrix K of 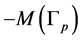 just by Gauss-Neumann diagonalization on the Laplacian matrix of
just by Gauss-Neumann diagonalization on the Laplacian matrix of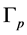 . This is the main result of this article.
. This is the main result of this article.
We want to conclude with an example of an application of our results for the topological field theory. In [3] [13] we built a set of graph manifolds whose Seifert invariants are constructed on the base of the first 9 prime numbers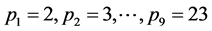 . The rational linking matrix of these graph manifolds are positive definite and have diagonal elements (and eigenvalues) simulating the low-energy coupling constants hierarchy of the fundamental interactions of real universe. An example of such matrix is [13]
. The rational linking matrix of these graph manifolds are positive definite and have diagonal elements (and eigenvalues) simulating the low-energy coupling constants hierarchy of the fundamental interactions of real universe. An example of such matrix is [13]
 whose elements are all rational and the diagonal ones are described in (14) and (17) by a sum of three continued fractions. The matrix
whose elements are all rational and the diagonal ones are described in (14) and (17) by a sum of three continued fractions. The matrix 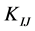 inverse to
inverse to 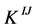 is integer one [6] , the inversion of the rational linking matrices can be done with the help of any program such as MathematicaTM to verify this property, any error on calculation of
is integer one [6] , the inversion of the rational linking matrices can be done with the help of any program such as MathematicaTM to verify this property, any error on calculation of 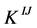 leads to non-integer elements in resulting matrices
leads to non-integer elements in resulting matrices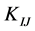 . It is also worth mentioning that in the present example the Laplacian block matrix
. It is also worth mentioning that in the present example the Laplacian block matrix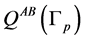 , corresponding to the matrix
, corresponding to the matrix , has
, has 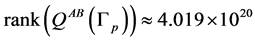 [13] , while
[13] , while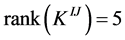 .
.
In the 7-dimensional Kaluza-Klein approach to the topological field theory (BF-model), the rational linking matrices of the 3-dimensional graph manifold may be really interpreted as coupling constants matrices [1] . So, the Gauss-Neumann method gives us a simple algorithm to calculate the linking matrices of graph manifolds and thus the coupling constants matrices (despite the probably huge rank of the original block matrix ).
).
References
- Verlinde, E. (1995) Global Aspects of Electric-Magnetic Duality. Nuclear Physics B, 455, 211-225. http://dx.doi.org/10.1016/0550-3213(95)00431-Q
- Efremov, V.N., Mitskievich, N.V., Hernandez Magdaleno, A.M. and Serrano Bautista, R. (2005) Topological Gravity on Plumbed V-Cobordisms. Classical and Quantum Gravity, 22, 3725-3744. http://dx.doi.org/10.1088/0264-9381/22/17/022
- Efremov, V.N., Hernandez Magdaleno, A.M. and Moreno, C. (2010) Topological Origin of the Coupling Constants Hierarchy in Kaluza-Klein Approach. International Journal of Modern Physics A, 25, 2699-2733. http://dx.doi.org/10.1142/S0217751X10048482
- Saveliev, N. (2002) Invariants for Homology3-Spheres. Springer, Berlin, 223. http://dx.doi.org/10.1007/978-3-662-04705-7
- Eisenbud, D. and Neumann, W. (1985) Three-Dimensional Link Theory and Invariants of Plane Curve Singularities. Princeton University Press, Princeton, 172.
- Saveliev, N. (2002) Fukumoto-Furuta Invariants of Plumbed Homology 3-Spheres. Pacific Journal of Mathematics, 205, 465-490. http://dx.doi.org/10.2140/pjm.2002.205.465
- Neumann, W. (1997) Commensurability and Virtual Fibration for Graph Manifolds. Topology, 36, 355-378. http://dx.doi.org/10.1016/0040-9383(96)00014-6
- Hirzebruh, F. (1971) Differentiable Manifolds and Quadratic Forms. Marcel Dekker, New York, 56-58.
- Neumann, W. (1981) A Calculus for Plumbing Applied to the Topology of Complex Surface Singularities and Degenerating Complex Curves. Transactions of the American Mathematical Society, 268, 299. http://dx.doi.org/10.1090/S0002-9947-1981-0632532-8
- Waldhausen, F. (1967) Eine Klasse Von 3-Dimensionalen Mannigfaltigkeiten. I. Inventiones Mathematicae, 3, 308-333. http://dx.doi.org/10.1007/BF01402956
- Popescu-Pampu, P. (2007) The Geometry of Continued Fractions and the Topology of Surface Singularities. In: Brasselet, J.-P. and Suwa, T., Eds., Singularities in Geometry and Topology 2004, Advanced Studies in Pure Mathematics, Vol. 46, 119-195.
- Beasley, C. and Witten, E. (2005) Non-Abelian Localization for Chern-Simons Theory. Journal of Differential Geometry, 70, 183-323.
- Efremov, V., Hernandez, A. and Becerra, F. (2014) The Universe as a Set of Topological Fluids with Hierarchy and Fine Tuning of Coupling Constants in Terms of Graph Manifolds. arXiv:1309.0690v2

