Applied Mathematics
Vol.05 No.12(2014), Article ID:47380,6 pages
10.4236/am.2014.512170
Two Fractal Regimes of the Soil Hydraulic Properties
Samuele De Bartolo1, Carmine Fallico1, Gerardo Severino2, Massimo Veltri1
1Department of Civil Engineering, University of Calabria, Rende, Italy
2Water Resources Management and Bio System Engineering, University of Naples “Federico II”, Portici, Naples, Italy
Email: samuele.debartolo@unical.it, severino@unina.it
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 26 March 2014; revised 29 April 2014; accepted 6 May 2014
ABSTRACT
A fractal analysis of the soil retention and hydraulic conductivity curves is presented. The reten- tion process is modeled by a two fractal regimes: one pertaining to high water content values, and another accounting for the low water content data. This significantly improves the physical insight of the retention process as compared with the case of one-fractal models. The fractal dimensions characterizing the two regimes are estimated by fitting the retention curve model upon real data, and subsequently they are used to determine the hydraulic conductivity which for the retention curve models of Mualem and Burdine, is obtained in closed form. The reliability of the model is tested against independent conductivity data collected in a field-scale campaign.
Keywords:
Fractal Dimension, Soil, Retention Curve, Conductivity Curve

1. Introduction
The hydraulic conductivity is a fundamental prerequisite: 1) to quantify the movement of water, and 2) to predict transport phenomena taking place in soils. Generally, the soil hydraulic conductivity is expressed by parameters which are fitted against in situ measurements. The range of variability of such parameters (especially the saturated conductivity) may span several orders of magnitude, and therefore is often very difficult to adequately predict the soil hydraulic conductivity from only direct measurements. One of the most successful strategies to determine the unsaturated hydraulic conductivity is to relate it to the water retention curve (WRC) [1] [2] which, unlike the conductivity technique, is determined by very robust and reliable procedures. This is because the parameters of the retention curve are the same appearing in the hydraulic conductivity (a wide review can be found in [3] and [4] ), and therefore once they are determined via the retention curve de facto also provide the hydraulic conductivity curve.
The functional relationship between water content and pressure head (negative for soils) defining the WRC has represented (and still represents) a vivid research topic [5] . In the past years, an important boost came from the fractal geometry [6] - [8] which was used to characterize the hydraulic conductivity by means of the fractal properties of pore spaces ( [9] [10] ). This has permitted relating the fractal dimension at low water content values to the physics of thin water films [11] either by combining Kock’s curve to the flow (Poiseuille) equation [12] , or by dealing with the fractal dimension of the porosity and a diffusion-type (Millington and Quirk) equation [13] . An exhaustive review of all these models can be found in ( [14] [15] and references therein).
In the present paper we regard the water retention mechanism as a two-fractal process, i.e. the water retention curve is hypothesized as two fractal dimensions: one related to low water contents, and the another accounting for the high water contents. The resulting WRCs are subsequently (analytically) integrated to obtain the soil conductivity curve. Finally, we test our model against real data.
2. The Two Regimes Fractal Model
We deal with the Burdine [1] and Mualem [2] WRC-models. The first writes as:
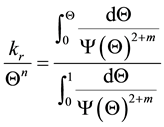 (1)
(1)
where Q is the normalized (also known as degree of saturation) volumetric water content, n and m are parameters which within the present paper (in line with the majority of the past studies) will be equal to 2 and 0. The second is:
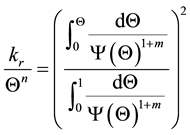 (2)
(2)
with n = 0.5 and m = 0. In Equations (1) and (2) the function Y = Y(Q) represents the relationship between the suction Y and Q. These models represent the outcome of theoretical as well as experimental studies relating the soil fractal structure to: 1) the particle size distribution [16] , 2) solid aggregate typology distribution [17] [18] , 3) pore-solid interface area [11] [19] , 4) pore-phase fractal mass [9] [20] , and 5) solid-phase fractal mass [21] [22] . In particular, Tyler and Wheatcraft [23] regard the water retention mechanism like a (Menger) sponge with 1 < D £ 2. A more realistic generalization of this model is given by Rieu and Sposito [21] leading to 2.090 £ D £ 2.963 [24] , and to 2.766 £ D £ 2.986 [21] . Unlike these studies (which detected a fractal dimension lesser than 3), Tyler and Wheatcraft [23] report 3.011 £ D £ 3.485. This was attributed to the impact of the distribution of smaller pores, and this topic shall be recalled within the present paper, as well.
It is well known that at high water contents the WRC is governed by the distribution of larger pores, while at the low water contents the WRC is determined by the thin water film on the solid particles [11] [14] [15] . This naturally calls for a two-fold fractal interpretation of the retention process. Thus, Millán and González-Posada [25] introduced a new fractal model by considering two fractal regimes: one (termed as structural) pertaining to high water contents, and another (textural) related to the low water contents. Similarly to Perfect [26] , the simplest (and most intuitive) way to employ such a model is as follows:
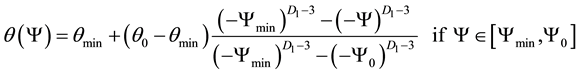 (3)
(3)
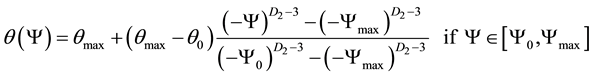 (4)
(4)
where the fractal dimensions D1 and D2 are determined by a best fitting procedure. In Equations (3) and (4) Ymax is the air entry value with qmax = q(Ymax). We regard Ymin as the maximum (absolute) value of the measured suction, being qmin the associated water content. This latter is like to be attached to the residual water content. Finally, the pair (Y0, q0) represents the turning-point where the fractal scaling (i.e. the change in the fractal dimension) changes. These values are determined by a best-fit procedure, which is carried out after re-defining the degree of saturation as follows:
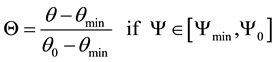 (5)
(5)
for the low, and:
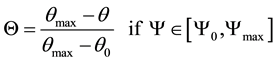 (6)
(6)
for the largest water content values, respectively. As it will be clearer later on, it is convenient to invert (3)-(4), the final result being:
 (7)
(7)
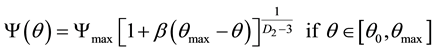 (8)
(8)
where:
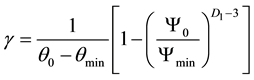 , (9)
, (9)
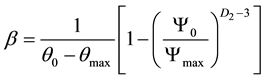 . (10)
. (10)
With the parameters (9)-(10) defined by means of the inversion (7)-(8), the Burdine’s model [1] is easily obtained:
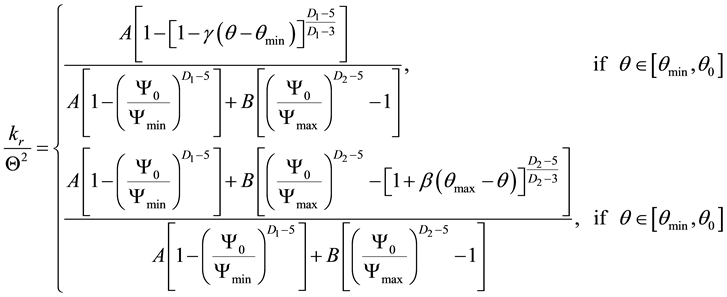 (11)
(11)
with:
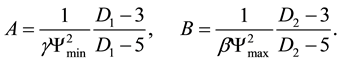 (12)
(12)
A similar procedure with the Mualem’s model [2] leads to:
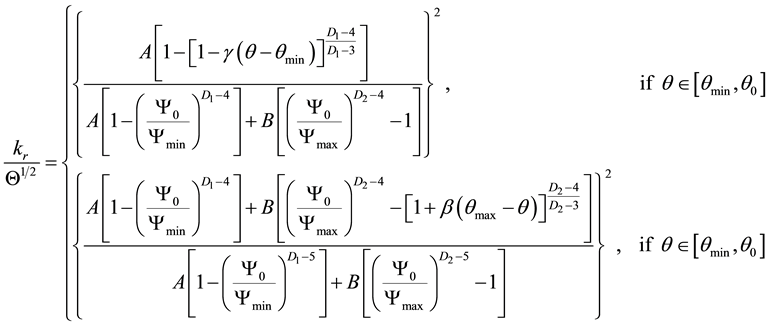 (13)
(13)
being
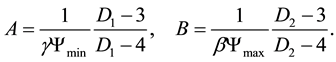 (14)
(14)
For the D1 = D2 = 3 (that is the case of) both (11) and (13) collapse (for brevity, the very lengthy algebraic derivations are not reported) into the early traditional one fractal model.
3. Results
The models derived in the previous section are tested against experimental data collected in a field scale experiment at the Ponticelli site (Italy). Details of the data-sampling and probing method can be reviewed in Severino et al. [27] (and references therein). The fractal dimensions of the WRCs (3) and (4) were estimated by a nonlinear regression, and the most important results are presented in Figure 1(a), Figure 2(a) and Figure 3(a), whereas the full analysis of the data-set is summarized in the Table 1.

Figure 1. (a) Water retention calibration; (b) Relative hydraulic conductivity vs the water content. The dashed line and continuous line refer to the Mualem and Burdine model, respectively (sample n. 1).
Table 1. Numerical results of the scaling non-linear regression analysis for the bifractal water retention curve model.

Figure 2. (a) Water retention calibration; (b) Relative hydraulic conductivity vs the water content. The dashed line and continuous line refer to the Mualem and Burdine model, respectively (sample n. 4).

Figure 3. (a) Water retention calibration; (b) Relative hydraulic conductivity vs the water content. The dashed line and continuous line refer to the Mualem and Burdine model, respectively (sample n. 5).
At a first glance the fitting was relatively good for almost all the cases. The values of D2 change considerably from the samples at 10 cm depth, where some values are found greater than 3 (and in some cases even greater than 4), to the samples at 90 cm depth where all the values of D2 are smaller than 3. A different situation is encountered with the values of the fractal dimension D1 that characterizes the low water content. Indeed, it doesn’t change considerably with the depth. The different behavior in the fractal regime is also emphasized by the mean of the two fractal dimensions being m1 < 3 and m2 > 3.5. In particular, the values of D1 obtained for the locations (1, 2, 3, 4, 5) and the values of D2 obtained for the locations (3, 4) resulted smaller than 3 in agreement with those reported in literature (see for example [20] [21] ). All the other results reported values greater than 3, and this is a similar result obtained by Tyler and Wheatcraft [16] [23] .
A fractal dimension greater than 3 can be explained in the so-called generalized (multi)fractal model [28] - [31] . This is not accounted by our model, therefore representing a limitation of it (see discussion in [32] ). Starting from the (calibrated) WRCs, the hydraulic conductivity is straightforwardly fully determined by means of (11) and (13). The theoretical models are compared against the experimental data collected during the campaign at the Ponticelli site, and results (corresponding to the WRCs considered in the Figure 1(a), Figure 2(a) and Figure 3(a)) are shown in the Figure 1(b), Figure 2(b) and Figure 3(b). Similarly to the WRCs, we have summarized the results that pertain to the full data-set in the Table 2.
Unlike sample 4 (where a very good agreement was detected for both the models), the (relative) difference between experimental and predicted conductivity-values ranges from 10% to 15%. It is seen that the both the models lead to two different hydraulic conductivity curves. In particular, the two-fractal conductivity model as derived from the Burdine-WRC is smaller (in the region of high water content values) than the co respective obtained from the Mualem’s WRC. Such a situation is reversed within the region of low water contents: the Mua-
Table 2. Numerical results of hydraulic conductivity analysis with the values of the perturba- tion error on the residual water content.
lem bifractal model gives smaller values for hydraulic conductivity than the Burdine model (see Figures 1-3).
4. Concluding Remarks
An analysis of the soil hydraulic properties by means of the fractal geometry has been presented. The models for the WRCs are based on a two-fractal regime [26] . Such a model allows for a better interpretation (as compared with the so-called one fractal models) of the water retention mechanism by relating the low values of the water contents to the smaller size of the fractal dimension. Another advantage of our model is that it leads to closed form conductivity curves without carrying out any conductivity-type measurements, which are very difficult to carry out. The two fractal regimes conductivity model is compared to real data collected during a very detailed field scale campaign. The matching between the calibrated conductivity curves is found excellent for the vast majority of the cases. The proposed model also opens toward possible generalizations such as accounting for a multi-fractal regime.
Acknowledgements
This research was partly supported by: 1) Solute Transport in Heterogeneous Media: Modelling and Computa- tional Aspects (Departmental found), and 2) PRIN (2010LE4NBM_007) project I paesaggi tradizionali dell’ agricoltura italiana: definizione di un modello interpretativo multidisciplinare e multiscala finalizzato alla pianificazione e alla gestione.
References
- Burdine, N.T. (1953) Relative Permeability Calculations from Pore Size Distribution Data. Journal of Petroleum Technology, 5, 71-78.
- Mualem, Y. (1976) A New Model for Predicting the Hydraulic Conductivity of Unsaturated Porous Media. Water Resources Research, 12, 513-522. http://dx.doi.org/10.1029/WR012i003p00513
- Brooks, R.H. and Corey, A.T. (1964) Hydraulic Properties of Porous Media. Hydrology Papers 3, Colorado State University, Fort Collins, 27 p.
- Van Genuchten, M.T. (1980) A Closed Form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Science Society of America Journal, 44, 892-898. http://dx.doi.org/10.2136/sssaj1980.03615995004400050002x
- Hunt, A., Ewing, R. and Ghambarian, B. (2014) Percolation Theory for Flow in Porous Media. 3rd Edition, Springer- Verlag. http://dx.doi.org/10.1007/978-3-319-03771-4
- Pachesky, Y.A., Shcherbakov, R.A. and Kursunskaya, L.P. (1995) Scaling of Soil Water Retention Using a Fractal Model. Soil Science, 159, 99-104. http://dx.doi.org/10.1097/00010694-199502000-00003
- Perrier, E., Rieu, M., Sposito, G. and de Marsily, G. (1996) Models of Water Retention Curve for Soils with a Fractal Pore Size Distribution. Water Resources Research, 32, 3025-3031. http://dx.doi.org/10.1029/96WR01779
- Fallico, C., Tarquis, A.M., De Bartolo, S. and Veltri, M. (2010) Scaling Analysis of Water Retention Curves for Unsaturated Sandy Loam Soils by Using Fractal Geometry. European Journal of Soil Science, 61, 425-436. http://dx.doi.org/10.1111/j.1365-2389.2010.01239.x
- Katz, A.J. and Thompson, A.H. (1985) Fractal Sandstone Pores: Implication for Conductivity and Pore Formation. Physical Review Letters, 54, 1325-1328. http://dx.doi.org/10.1103/PhysRevLett.54.1325
- Hansen, J.P. and Skjeltorp, A.T. (1988) Fractal Pore Space and Rock Permeability Implications. Physical Review B, 38, 2635-2638. http://dx.doi.org/10.1103/PhysRevB.38.2635
- Toledo, P.G., Novy, R.A, Davis, H.T. and Scriven, L.E. (1990) Hydraulic Conductivity of Porous Media at Low Water Content. Soil Science Society of America Journal, 54, 673-679. http://dx.doi.org/10.2136/sssaj1990.03615995005400030007x
- Shepard, S.J. (1993) Using a Fractal Model to Compute the Hydraulic Conductivity Function. Soil Science Society of America Journal, 57, 300-306. http://dx.doi.org/10.2136/sssaj1993.03615995005700020002x
- Xu, Y.F. and Dong, P. (2004) Fractal Approach to Hydraulic Properties in Unsaturated Porous Media. Chaos, Solitons and Fractals, 19, 327-337.
- Gimenez, D., Perfect, E., Rawls, W.J. and Pachepsky, Y. (1997) Fractal Models for Predicting Soil Hydraulic Properties: A Review. Reviews in Engineering Geology, 48, 161-183. http://dx.doi.org/10.1016/S0013-7952(97)00038-0
- Ghanbarian-Alavijeh, B., Millán, U. and Huang, G. (2011) A Review of Fractal, Prefractal and Pore-Solid-Fractal Models for Parametrizing the Soil Water Retention Curve. Canadian Journal of Soil Science, 91, 1-14. http://dx.doi.org/10.4141/cjss10008
- Tyler, S.W. and Wheatcraft, S.W. (1989) Application of Fractal Mathematics to Soil Water Retention Estimation. Soil Science Society of American Journal, 53, 987-996. http://dx.doi.org/10.2136/sssaj1989.03615995005300040001x
- Perfect, E. and Kay, B.D. (1991) Fractal Theory Applied to Soil Aggregation. Soil Science Society of America Journal, 55, 1552-1558. http://dx.doi.org/10.2136/sssaj1991.03615995005500060009x
- Crawford, J.W., Sleeman, B.D. and Young, I.M. (1993) On the Relation between Number Size Distribution and the Fractal Dimension of Aggregates. Journal of Soil Science, 44, 555-565. http://dx.doi.org/10.1111/j.1365-2389.1993.tb02321.x
- De Gennes, P.G. (1985) Partial Filling of a Fractal Structure by a Wetting Fluid. In: Adler, D., Frietzsche, E. and Ovshinsky, S.R., Eds., Physics of Disordered Materials, Plenum Press, New York, 227-241.
- Bird, N.R.A., Bartoli, F. and Dexter, A.R. (1996) Water Retention Models for Fractal Soil Structures. European Jour- nal of Soil Science, 47, 1-6. http://dx.doi.org/10.1111/j.1365-2389.1996.tb01365.x
- Rieu, M. and Sposito, G. (1991) Fractal Fragmentation, Soil Porosity, and Soil Water Properties: I. Theory. Soil Science Society of America Journal, 55, 1231-1238. http://dx.doi.org/10.2136/sssaj1991.03615995005500050006x
- Crawford, J.W. (1994) The Relationship between Structure and the Hydraulic Conductivity of Soil. European Journal of Soil Science, 45, 493-501. http://dx.doi.org/10.1111/j.1365-2389.1994.tb00535.x
- Tyler, S.W. and Wheatcraft, W. (1990) Fractal Processes in Soil Water Retention. Water Resources Research, 26, 1047-1054. http://dx.doi.org/10.1029/WR026i005p01047
- Huang, G.H. and Zhang, R.D. (2005) Evaluation of Soil Water Retention Curve with the Pore Solid Fractal Approach. Geoderma, 127, 52-61. http://dx.doi.org/10.1016/j.geoderma.2004.11.016
- Millán, H. and González-Posada, M. (2005) Modelling Soil Water Retention Scaling. Comparison of a Classical Fractal Model with a Piecewise Approach. Geoderma, 125, 25-38. http://dx.doi.org/10.1016/j.geoderma.2004.06.003
- Perfect, E. (1999) Estimating Soil Mass Fractal Dimensions from Water Retention Curves. Geoderma, 88, 221-231. http://dx.doi.org/10.1016/S0016-7061(98)00128-1
- Severino, G., Santini, A. and Sommella, A. (2003) Determining the Soil Hydraulic Conductivity by Means of a Field Scale Internal Drainage. Journal of Hydrology, 273, 234-248. http://dx.doi.org/10.1016/S0022-1694(02)00390-6
- Renyi, A. (1970) Probability Theory. North-Holland Publishing, Budapest.
- Hentschel, H.G.E. and Procaccia, I. (1983) The Infinite Number of Generalized Dimensions of Fractals and Strange Attractors. Physica D, 8, 435-444. http://dx.doi.org/10.1016/0167-2789(83)90235-X
- Grassberger, P. (1983) Generalized Dimensions of Strange Attractors. Physics Letters A, 97, 227-230. http://dx.doi.org/10.1016/0375-9601(83)90753-3
- Grassberger, P. and Procaccia, I. (1983) Characterization of Strange Attractors. Physical Review Letters, 50, 346-349. http://dx.doi.org/10.1103/PhysRevLett.50.346
- Halsey, T.C., Jensen, M.H., Kadanoff, L.P., Procaccia, I. and Shraiman, B.I. (1986) Fractal Measures and Their Singu- larities: The Characterization of Strange Sets. Physical Review A, 33, 1141-1151. http://dx.doi.org/10.1103/PhysRevA.33.1141





