Received 14 March 2014; revised 14 April 2014; accepted 21 April 2014

ABSTRACT

In this paper, the Adomian decomposition method with Green’s function (Standard Adomian and Modified Technique) is applied to solve linear and nonlinear tenth-order boundary value problems with boundary conditions defined at any order derivatives. The numerical results obtained with a small amount of computation are compared with the exact solutions to show the efficiency of the method. The results show that the decomposition method is of high accuracy, more convenient and efficient for solving high-order boundary value problems.

Keywords:

Adomian decomposition method, Adomian’s polynomials, Tenth-order boundary value problems, Green’s function

1. Introduction

In the beginning of the 1980’s, Adomian [1] -[4] proposed a new and fruitful method (hereafter called the Adomian Decomposition Method or ADM) for solving linear and nonlinear (algebraic, differential, partial differential, integral, etc.) equations. It has been shown that this method yields a rapid convergence of the solutions series to linear and nonlinear deterministic and stochastic equations.

The lower-order boundary value problems have been vastly examined, analytically and numerically, in the literature. In contrast, higher-order boundary value problems have not been studied to the same extent that lower- order equations have been investigated. Nowadays, higher-order boundary value problems receive an increased interest due to the fact that they are noted in many mathematical physics applications. A class of characteristic- value problems of high order (as high as twenty four) are known to arise in hydrodynamic and hydromagnetic stability [5] . Tenth-order differential equations govern the physics of some hydrodynamic stability problems. When an infinite horizontal layer of fluid is heated from below, with the supposition that a uniform magnetic field is also applied across the fluid in the same direction as gravity and the fluid is subject to the action of rotation, instability sets in. When this instability sets in as ordinary convection, it is modelled by a tenth-order ordinary differential equation [5] .

Theorems which list the conditions for the existence and uniqueness of solutions of BVPs of higher order are thoroughly investigated in a book by Agarwal [6] . However, no numerical methods are contained in [6] for solving such problems.

Different numerical and semi analytical methods have been proposed by various authors to solve tenth-order boundary-value problems. A few of them are: Tenth degree spline method [7] , Modified Decomposition Method with the inverse operator (MDM) [8] , Differential Transform Method (DTM) [9] , Eleventh Degree Spline Method (EDSM) [10] , Non-Polynomial Spline Method (NPSM) [11] , Variational Iteration Technique (VIT) [12] and Homotopy Perturbation Method (HPM) [13] .

The main objective of this paper is to apply the Standard Adomian with Green’s function (SAwGF) and Modified Technique with Green’s function (MTwGF) to linear and nonlinear tenth-order boundary value problems with boundary conditions defined at any order derivatives.

2. Analysis of the Method

Let us consider the general BVP of tenth-order

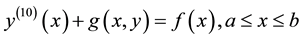(1)

with boundary conditions

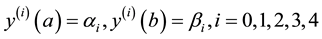(2)

where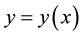, 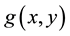is a linear or nonlinear function of, and 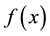are continuous functions de-

fined in the interval and,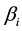; are finite real constants.

Applying the decomposition method as in [1] -[4] , Equation (1) can be written as

,

where 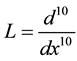is the linear operator and 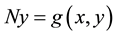is the nonlinear operator. Consequently,

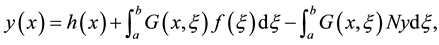(3)

where is the solution of 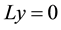with the boundary conditions (2) and is the Green’s function [14] given by

The Adomian’s technique consists of approximating the solution of (1) as an infinite series

(4)

and decomposing the nonlinear operator N as

(5)

where are polynomials (called Adomian polynomials) of [1] - [4] given by

The proofs of the convergence of the series and are given in [3] [15] - [19] . Substituting (4)

and (5) into (3) yields

(6)

From (6), the iterates defined using the Standard Adomian Method are determined in the following recursive way:

and the iterates defined using the Modified Technique [20] are determined in the following recursive way:

Thus all components of can be calculated once the are given. We then define the n-term approximant

to the solution by with.

3. Applications and Numerical Results

In this section, the ADM with the Green’s function (Standard Adomian and Modified Technique) for solving linear and nonlinear tenth-order boundary value problems is illustrated in the following examples. To show the high accuracy of the solution results compared with the exact solution, we give the maximum absolute error and the maximum residual error. The computations associated with the examples were performed using a Maple 13 package with a precision of 40 dígits.

3.1. Example 1

Consider the following linear BVP of tenth-order [9] - [12] :

(7)

with boundary conditions

(8)

The exact solution of (7), (8) is

Applying the decomposition method, Equation (7) can be written as

,

where is the linear operator. Consequently,

(9)

where is the solution of with the boundary conditions (8) given by

and is the Green’s function given by

where

Substituting (4) in (9), the iterates defined using the Standard Adomian Method are determined in the following recursive way:

and the iterates defined using the Modified Technique [20] are determined in the following recursive way:

In Table 1, we list the maximum errors obtained by SAwGF and MTwGF with the exact solution. Comparing them with the DTM [9] , EDSM [10] , NPSM [11] and VIT [12] results, we notice that the result obtained by the present method (SAwGF) is very superior (lower error combined with less number of iterations) to that obtained by the other mentioned methods. Table 2 reproduces the maximum residual error of the SAwGF and MTwGF for.

3.2. Example 2

Consider the following linear BVP of tenth-order [9] - [12] :

(10)

with boundary conditions

(11)

The exact solution of (10), (11) is

Applying the decomposition method, Equation (10) can be written as

,

where is the linear operator. Consequently,

(12)

where is the solution of with the boundary conditions (11) given by

and is the Green’s function given previously in example 1. Substituting (4) in (12), the iterates defined using the Standard Adomian Method are determined in the following recursive way:

and the iterates defined using the Modified Technique [20] are determined in the following recursive way:

In Table 3, we present the maximum errors obtained by SAwGF and MTwGF with the exact solution. Comparing them with the DTM [9] , EDSM [10] , NPSM [11] and VIT [12] results, it can be noticed that the result obtained by the present method (SAwGF) is very superior to that obtained by the other mentioned methods. Table 4 exhibits the maximum residual error of the SAwGF and MTwGF for.

3.3. Example 3

Consider the following linear BVP of tenth-order [10] :

(13)

with boundary conditions

(14)

The exact solution of (13), (14) is

Applying the decomposition method, Equation (13) can be written as

,

where is the linear operator. Consequently,

(15)

where is the solution of with the boundary conditions (14) given by

and is the Green’s function given previously in example 1. Substituting (4) in (15), the iterates defined using the Standard Adomian Method are determined in the following recursive way:

and the iterates defined using the Modified Technique [20] are determined in the following recursive way:

.

In Table 5, we give the maximum errors obtained by SAwGF and MTwGF with the exact solution. Comparing them with the EDSM [10] results, it can be seen easily that the result obtained by the present method (SAwGF) is very superior to that obtained by the other mentioned method. Table 6 reproduces the maximum residual error of the SAwGF and MTwGF for.

3.4. Example 4

Finally, we consider the following nonlinear BVP of tenth-order [8] [13] :

(16)

with boundary conditions

(17)

The exact solution of (16), (17) is

Applying the decomposition method, Equation (16) can be written as

,

where is the linear operator and is the nonlinear operator. Consequently,

(18)

where is the solution of with the boundary conditions (17) given by

and is the Green’s function given by

where

Substituting (4) and (5) in (18), the iterates defined using the Standard Adomian Method are determined in the following recursive way:

For the nonlinear term the corresponding Adomian polynomials are:

In Table 7, we list the maximum errors obtained by SAwGF with the exact solution. Comparing it with the MDM with the inverse operator [8] and HPM [13] results, it can be noticed that the result obtained by the present method (SAwGF) is very superior to that obtained by the other two mentioned methods. Table 8 exhibits the maximum residual error of the SAwGF for.

4. Conclusion

The ADM with Green’s function (Standard Adomian and Modified Technique) has been applied for solving linear and nonlinear tenth-order boundary value problems with boundary conditions defined at any order derivatives. Comparison of the results obtained by the present method with those obtained by the Tenth degree spline method, Modified decomposition method with the inverse operator, Differential transform method, Eleventh degree spline method, Non-polynomial spline method, Variational iteration technique and Homotopy perturbation method has revealed that the present method is superior because of the lower error and fewer required iterations. It has been shown that error is monotonically reduced with the increment of the integer n.

References