Applied Mathematics
Vol.4 No.12A(2013), Article ID:41077,7 pages DOI:10.4236/am.2013.412A006
The Triangular Hermite Finite Element Complementing the Bogner-Fox-Schmit Rectangle
1Institute of Computational Modeling, Siberian Branch of Russian Academy of Sciences, Krasnoyarsk, Russia
2Beihang University, Beijing, China
3Siberian Federal University, Krasnoyarsk, Russia
Email: shaidurov04@mail.ru
Copyright © 2013 Lidia Gileva et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2013 are reserved for SCIRP and the owner of the intellectual property Lidia Gileva et al. All Copyright © 2013 are guarded by law and by SCIRP as a guardian.
Received October 20, 2013; revised November 20, 2013; accepted November 27, 2013
Keywords: Continuously Differentiable Finite Elements; Bogner-Fox-Schmit Rectangle; Triangular Hermite Element
ABSTRACT
The Bogner-Fox-Schmit rectangular element is one of the simplest elements that provide continuous differentiability of an approximate solution in the framework of the finite element method. However, it can be applied only on a simple domain composed of rectangles or parallelograms whose sides are parallel to two different straight lines. We propose a new triangular Hermite element with 13 degrees of freedom. It is used in combination with the Bogner-Fox-Schmit element near the boundary of an arbitrary polygonal domain and provides continuous differentiability of an approximate solution in the whole domain up to the boundary.
1. Introduction
The finite elements with inter-elemental continuous differentiability are more complicated than those providing only continuity. Such two-dimensional elements are mostly developed for triangles: the Argyris triangle [1], the Bell reduced triangle [2], the family of Morgan-Scott triangles [3], the Hsieh-Clough-Tocher macrotriangle [4], the reduced Hsieh-Clough-Tocher macrotriangle [5], the family of Douglas-Dupont-Percell-Scott triangles [6], and the Powell-Sabin macrotriangles [7]. The Fraeijs de Veubeke-Sander quadrilateral [8] and its reduced version [9] are also composed of triangles. As for single, noncomposite rectangles, the Bogner-Fox-Schmit (BFS) element [10] is the most popular and simplest one in the family of elements discribed by Zhang [11]. All these elements are widely used in the conforming finite element method for the biharmonic equation and other equations of the fourth order (see for example [12-18] and references therein) along with mixed statements of problems and a nonconforming approach [12,14,17].
A direct application of the BFS-element is restricted to the case of a simple domain that is composed of rectangles or parallelograms whose sides are parallel to two different straight lines. This condition fails even in the case of a simple polygonal domain where the intersection of the boundary with rectangles results in triangular cells (cf. Figure 1). Of course, one can construct the special triangulation compatible with the boundary as some isoparametric image [19] of a domain composed of rectangles with sides parallel to the axes. This way requires solving some additional boundary value problems for the construction of such a mapping that is smooth over the whole domain.
In this paper we suggest to use the BFS-elements in the direct way (without an isoparametric mapping) for a couple with the proposed triangular Hermite elements with 13 degrees of freedom. These triangular elements supplement BFS-elements in the following sense. They are used only near the boundary of a polygonal domain and provide inter-element continuous differentiability between finite elements of these two types. Thus, due to the joint use of these elements on a polygonal domain , the approximate solution of finite element method belongs to the class
, the approximate solution of finite element method belongs to the class 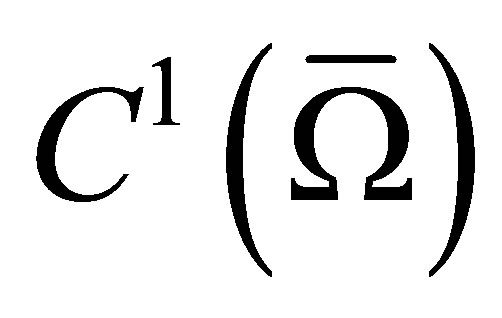 of functions which are continuously differentiable on the closure
of functions which are continuously differentiable on the closure  of the domain.
of the domain.

Figure 1. A subdivision of a domain.
2. Triangulation of a Domain and the Bogner-Fox-Schmit Element
Let 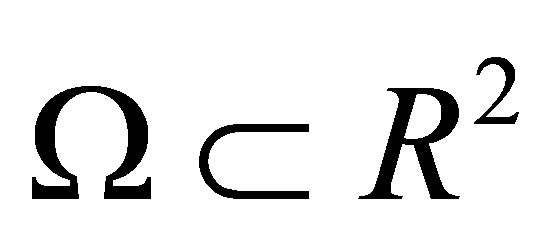 be a convex polygon with a boundary
be a convex polygon with a boundary  Assume that we can construct a triangulation
Assume that we can construct a triangulation 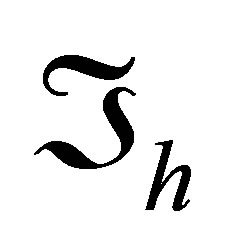 of
of  subdividing it into closed rectangular and triangular cells so that the most of them are rectangles and only a part of the cells adjacent to the boundary may be rectangular triangles. Besides, any two cells of
subdividing it into closed rectangular and triangular cells so that the most of them are rectangles and only a part of the cells adjacent to the boundary may be rectangular triangles. Besides, any two cells of  may not have a common interior point and any two triangular cells may not have a common side. In addition, the union of all the cells coincides with
may not have a common interior point and any two triangular cells may not have a common side. In addition, the union of all the cells coincides with 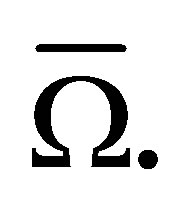 A simple example of the triangulation is shown in Figure 1. We also assume that all sides of the rectangular cells and the catheti of the triangular cells are parallel to the axes.
A simple example of the triangulation is shown in Figure 1. We also assume that all sides of the rectangular cells and the catheti of the triangular cells are parallel to the axes.
Denote by  the maximal diameter of all meshes
the maximal diameter of all meshes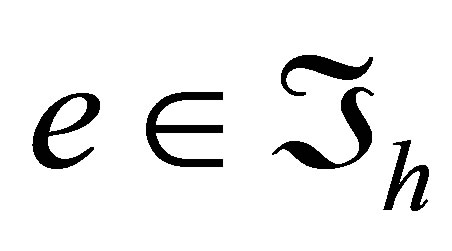 . On rectangular cells we use the Bogner-FoxSchmit element [1]. It is defined by the triple
. On rectangular cells we use the Bogner-FoxSchmit element [1]. It is defined by the triple 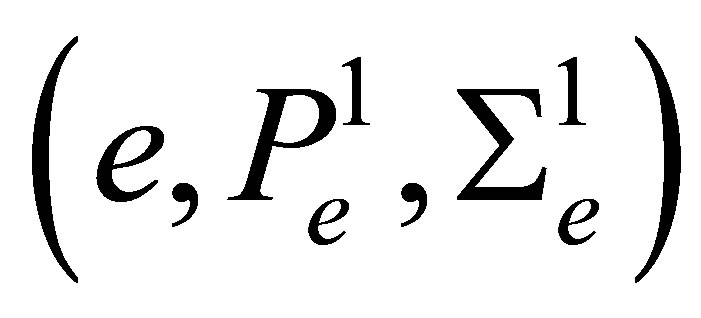
where  is the rectangle with vertices
is the rectangle with vertices 

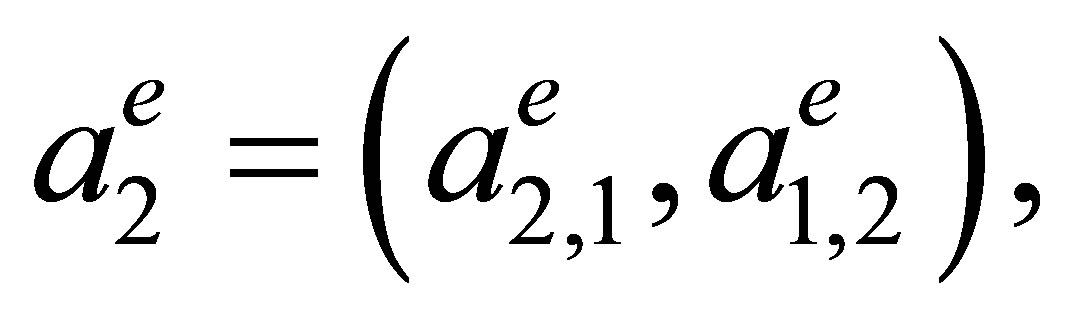 and
and 
and with side lengths  and
and 
Besides,  is the space of bicubic polynomials on
is the space of bicubic polynomials on 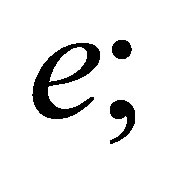 and
and 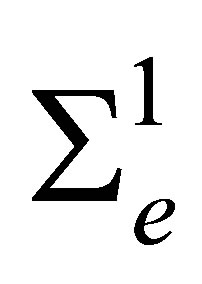 is the set of linear functionals (degrees of freedom or nodal parameters) of the form [12]
is the set of linear functionals (degrees of freedom or nodal parameters) of the form [12]
 (1)
(1)
The dimension of 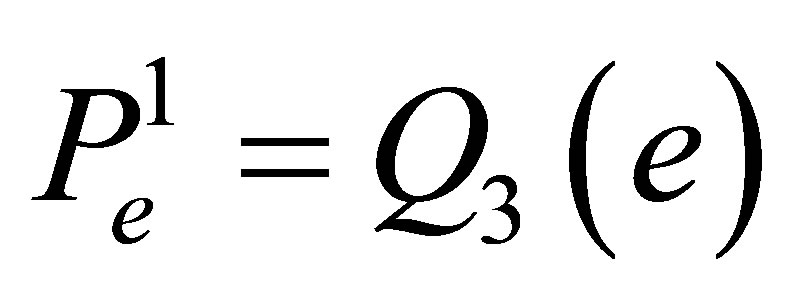 (the number of the coefficients of a polynomial) is equal to 16 and coincides with the number of the degrees of freedom. For this element we have the Lagrange basis in
(the number of the coefficients of a polynomial) is equal to 16 and coincides with the number of the degrees of freedom. For this element we have the Lagrange basis in 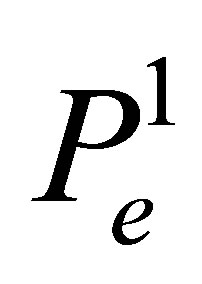 that consists of the functions
that consists of the functions 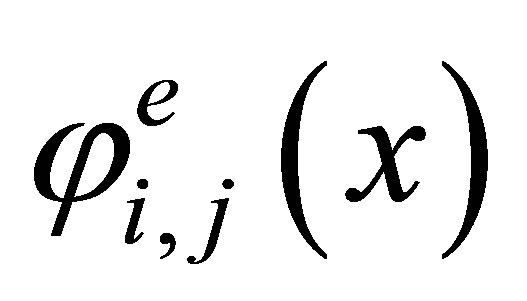
 satisfying the condition
satisfying the condition
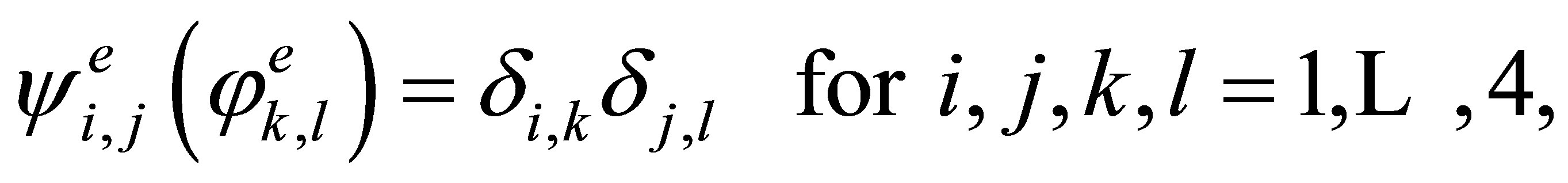 (2)
(2)
where  is the Kronecker delta. These functions can be written in the explicit form with the help of the one-dimensional splines
is the Kronecker delta. These functions can be written in the explicit form with the help of the one-dimensional splines

Indeed, the direct calculations show that the basis has the form
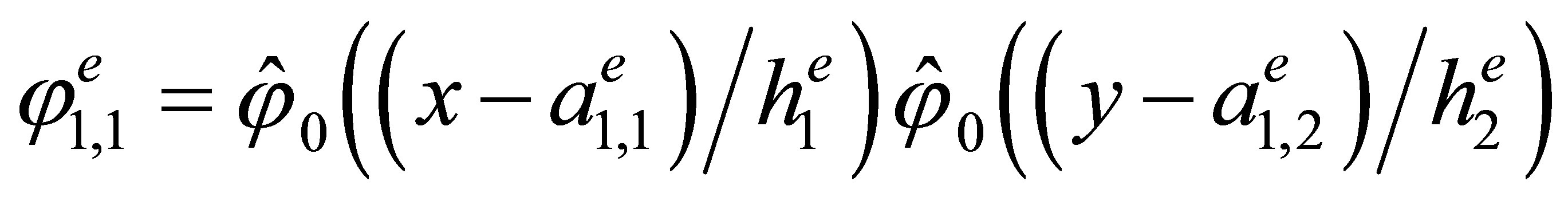 ,
,
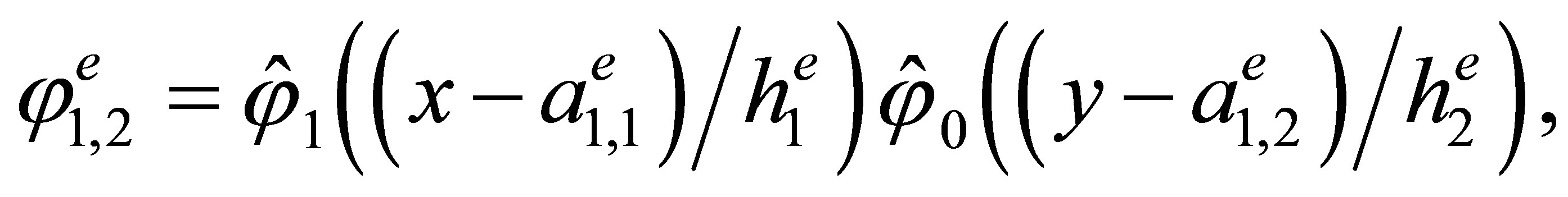



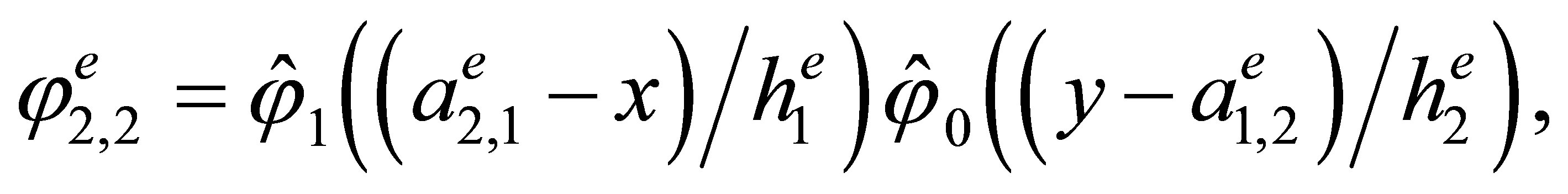


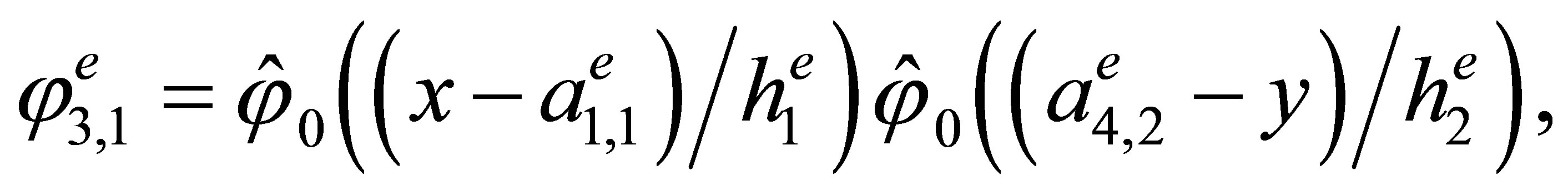

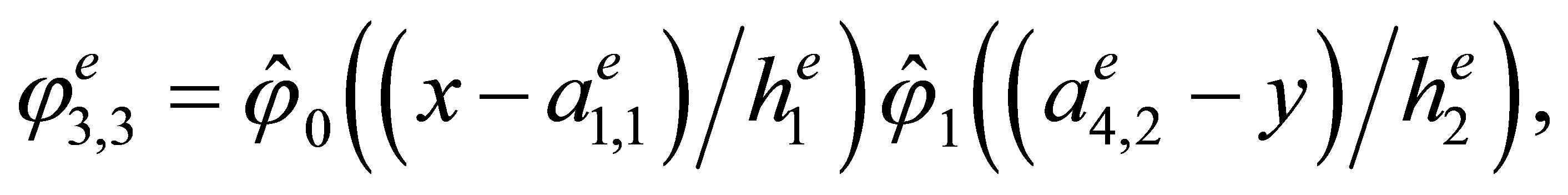
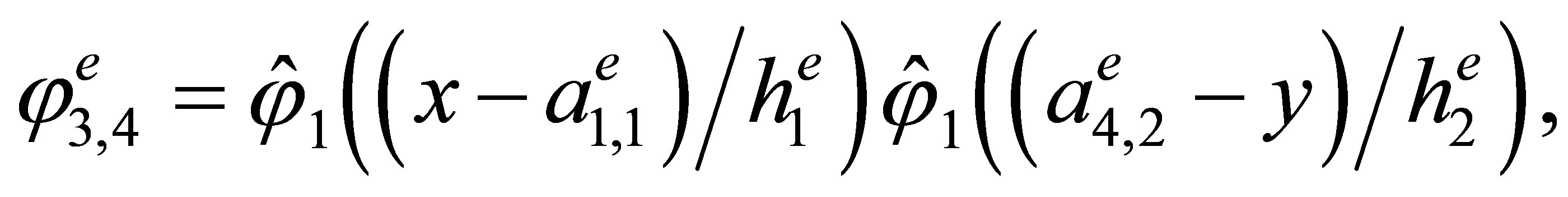
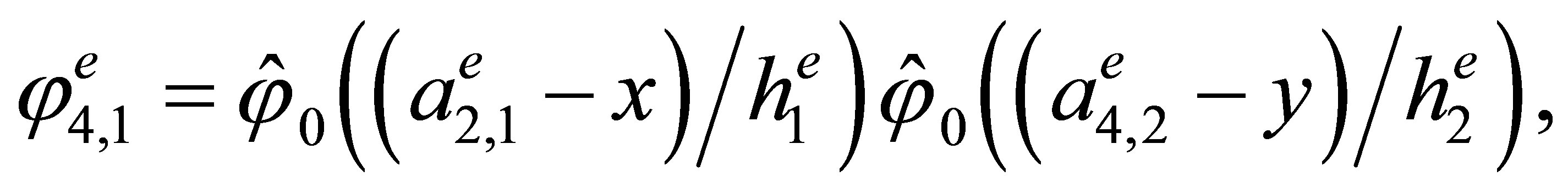

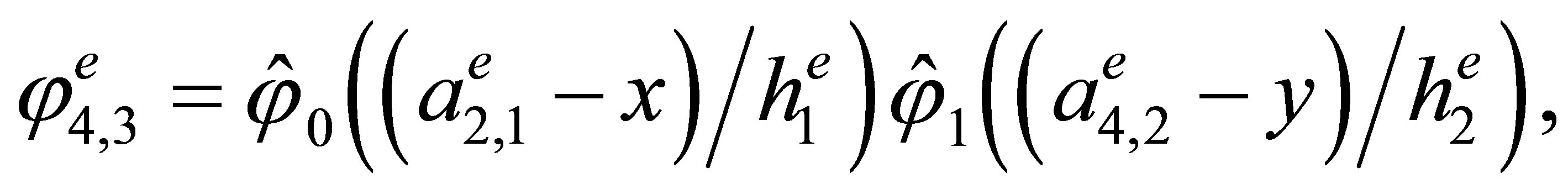
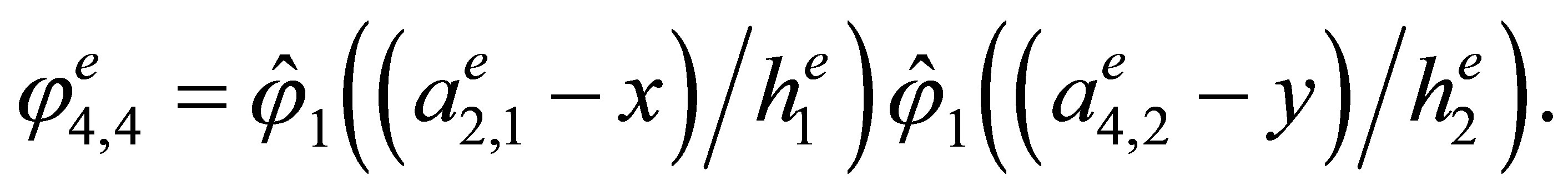
3. The “Reference” Triangular Hermite Element
First we construct the “reference” triangular element 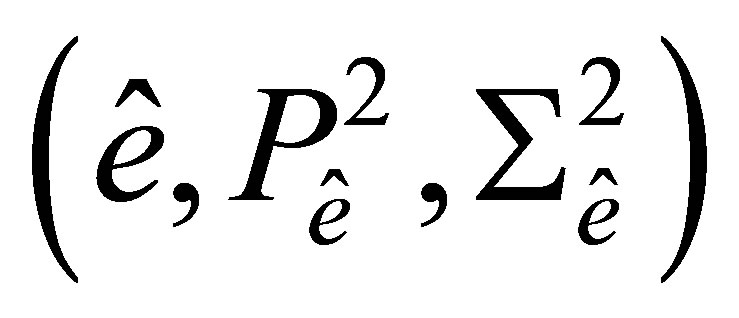 with the specified properties. We consider the right triangle
with the specified properties. We consider the right triangle  which has 4 nodes
which has 4 nodes  with the coordinates (0, 0), (1, 0), (0.5, 0.5), and (0, 1), respectively (Figure 2).
with the coordinates (0, 0), (1, 0), (0.5, 0.5), and (0, 1), respectively (Figure 2).
We define the space 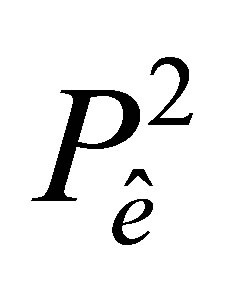 of functions and the set
of functions and the set  of degrees of freedom as follows:
of degrees of freedom as follows:
 (3)
(3)

Figure 2. The “reference” triangular element.
Observe that at each of the nodes , and
, and  there are 4 degrees of freedom and at the node
there are 4 degrees of freedom and at the node  there is only one degree. Besides, the degrees of freedom for the nodes
there is only one degree. Besides, the degrees of freedom for the nodes , and
, and  coincide with those for the nodes of the BFS-element (1).
coincide with those for the nodes of the BFS-element (1).
Lemma 1. The triple 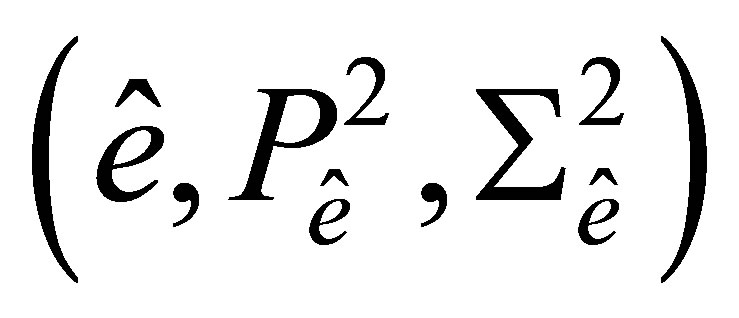 is a finite element.
is a finite element.
Proof. The dimension of the space  coincides with the number of elements of the set
coincides with the number of elements of the set 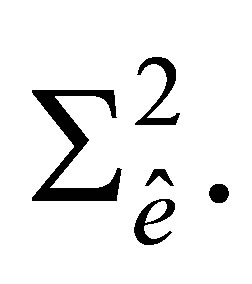 Hence, to prove unisolvence of the couple
Hence, to prove unisolvence of the couple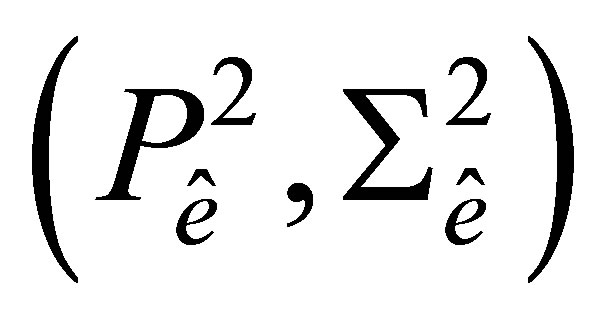 , it is sufficient to construct the Lagrange basis {
, it is sufficient to construct the Lagrange basis {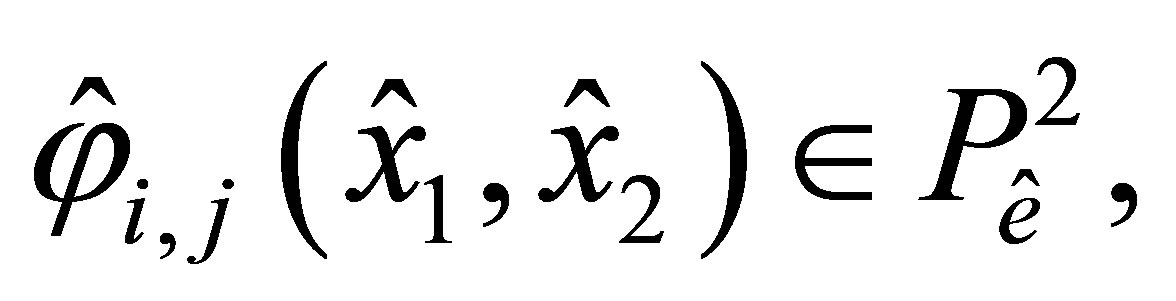 where
where 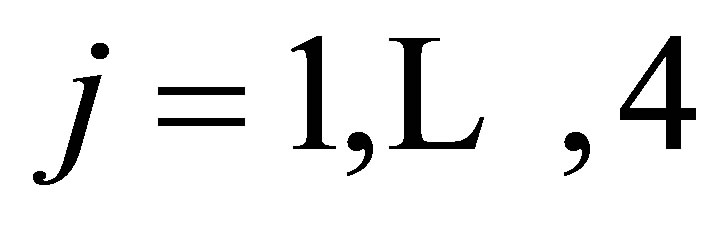 for i = 1, 2, 4 and j = 1 for
for i = 1, 2, 4 and j = 1 for 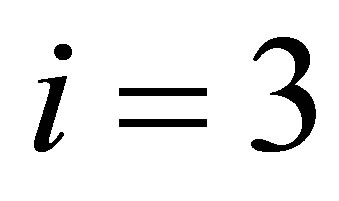 } on
} on  satisfying the condition [12]
satisfying the condition [12]
 (4)
(4)
The direct calculations show that the Lagrange basis has the following form:
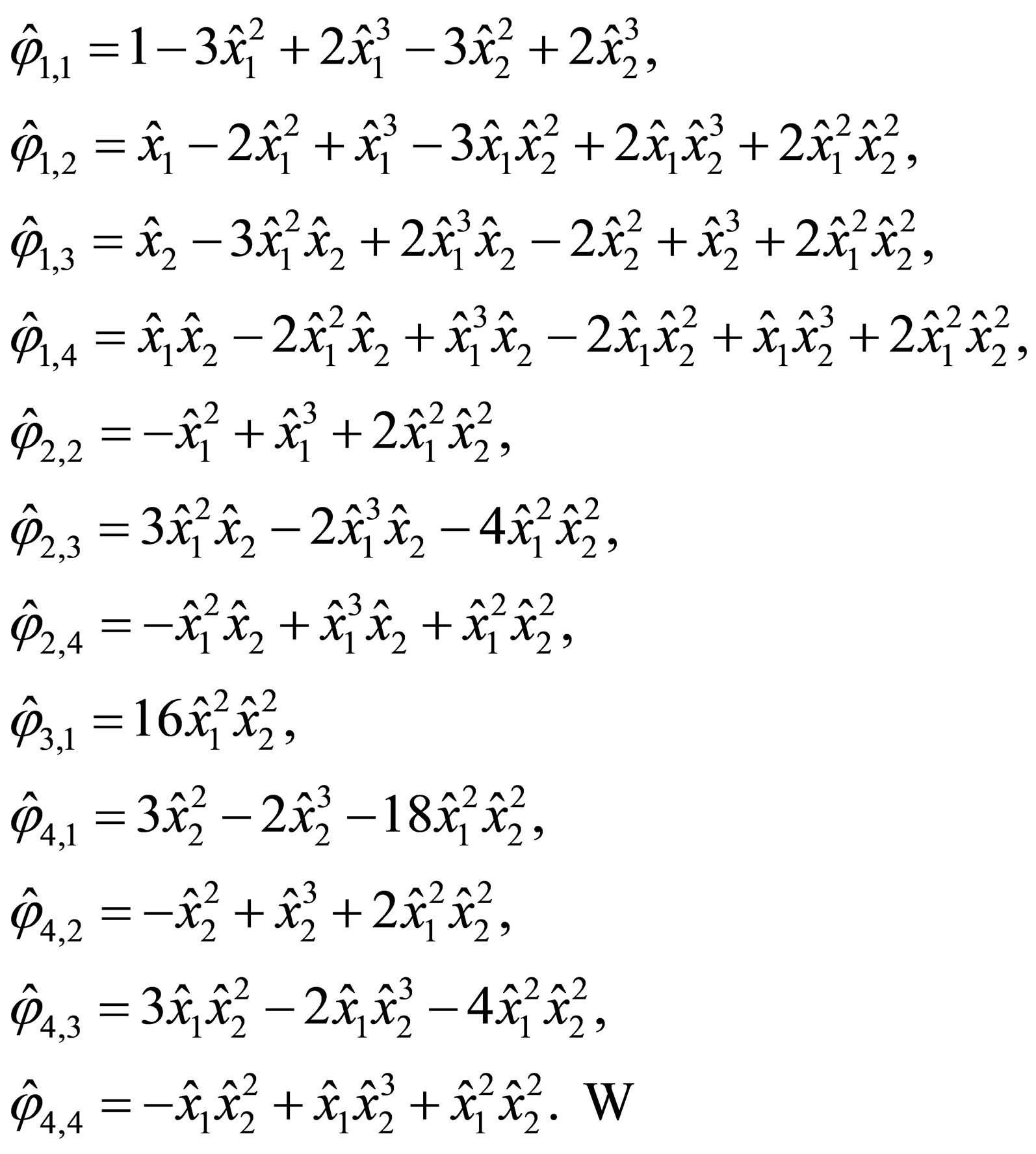 (5)
(5)
Let 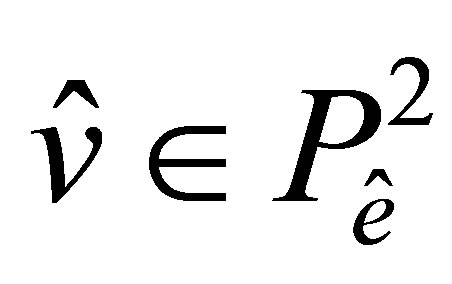 be an arbitrary function. Along the side
be an arbitrary function. Along the side  it is a polynomial of degree 3 in
it is a polynomial of degree 3 in 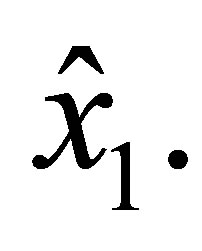 Together with the derivative
Together with the derivative  it is uniquely determined by the values
it is uniquely determined by the values , and
, and 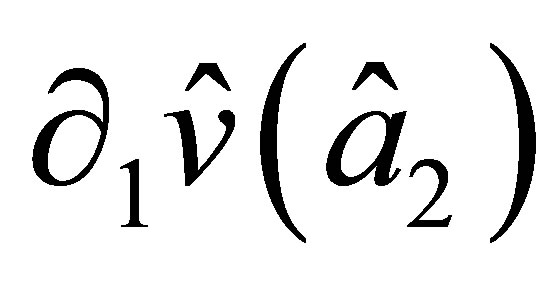 of nodal parameters. In addition, the derivative
of nodal parameters. In addition, the derivative  along
along 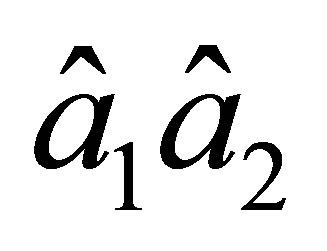 is a polynomial of degree 3 in
is a polynomial of degree 3 in 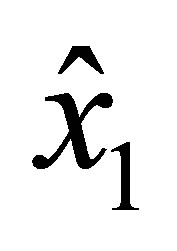 as well and is uniquely determined by the values
as well and is uniquely determined by the values and
and  of nodal parameters. On the side
of nodal parameters. On the side 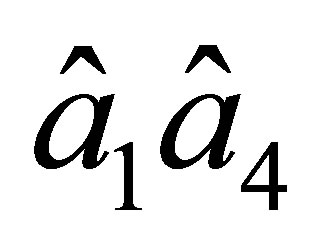
similar statements are valid within the replacement of 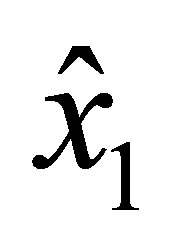 by
by 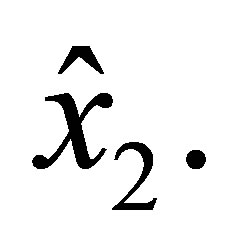
Thus, on the sides 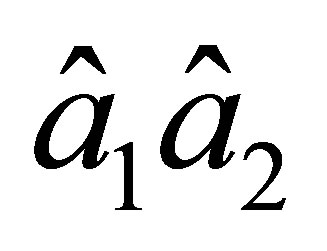 and
and 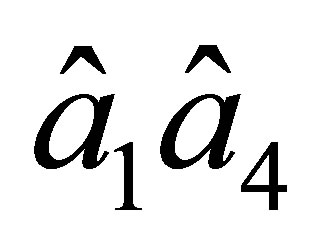 the values of a function of
the values of a function of 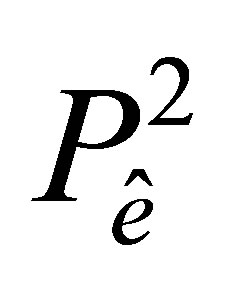 and its first-order partial derivatives are uniquely determined by the values of nodal parameters of
and its first-order partial derivatives are uniquely determined by the values of nodal parameters of  at the nodes on the corresponding side.
at the nodes on the corresponding side.
On the side 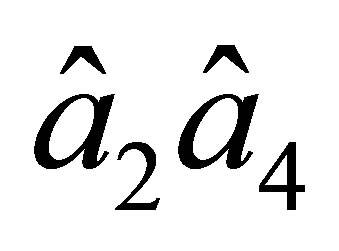 a similar property does not hold. Generally speaking, the element
a similar property does not hold. Generally speaking, the element  is not of the class
is not of the class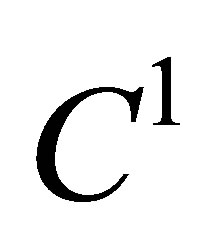 . This follows from the fact that the firstorder partial derivatives of the basis functions related to the node
. This follows from the fact that the firstorder partial derivatives of the basis functions related to the node 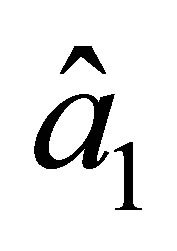 do not vanish on the side
do not vanish on the side . However, further we assume that the side of any triangular element of
. However, further we assume that the side of any triangular element of  being the image of the hypotenuse
being the image of the hypotenuse  is a part of the boundary and can not be a common side of two meshes. Hence, this feature has no influence on interelemental continuity inside the domain.
is a part of the boundary and can not be a common side of two meshes. Hence, this feature has no influence on interelemental continuity inside the domain.
To check the interpolation properties, we use the usual notations for Sobolev spaces. Here  is the Hilbert space of functions, Lebesgue measurable on
is the Hilbert space of functions, Lebesgue measurable on 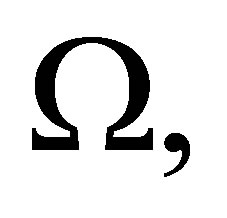 equipped with the inner product
equipped with the inner product

and the finite norm
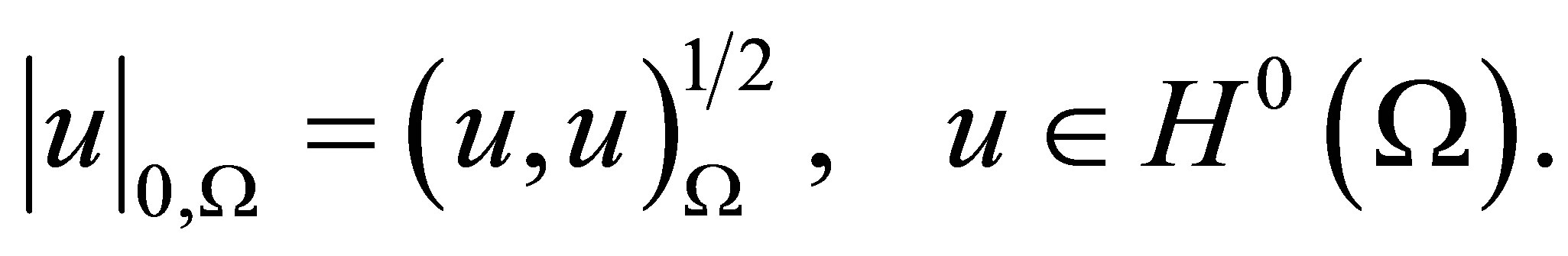
For integer nonnegative 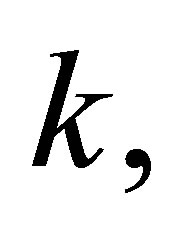
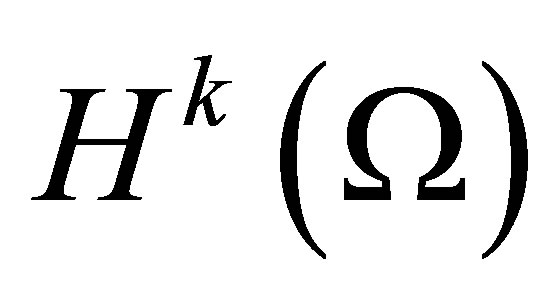 is the Hilbert space of functions
is the Hilbert space of functions 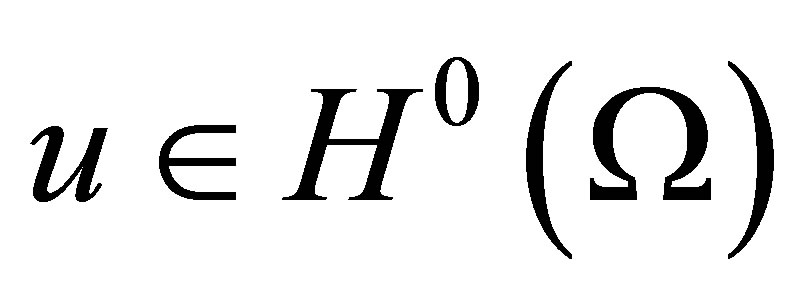 whose weak derivatives up to order
whose weak derivatives up to order 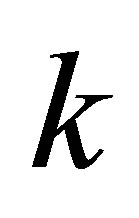 inclusive belong to
inclusive belong to . The norm in this space is defined by the formula
. The norm in this space is defined by the formula
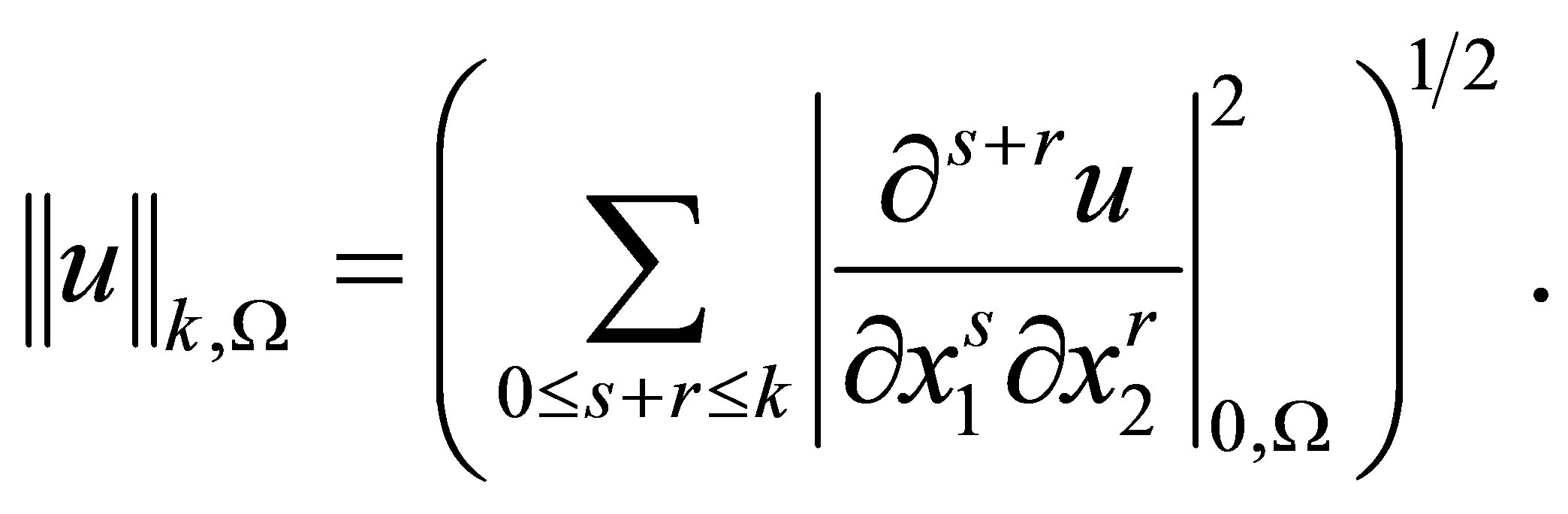
We also use the seminorm

Let  be an arbitrary function of
be an arbitrary function of 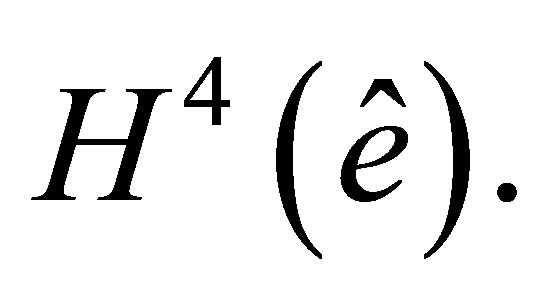 By a Sobolev embedding theorem,
By a Sobolev embedding theorem, 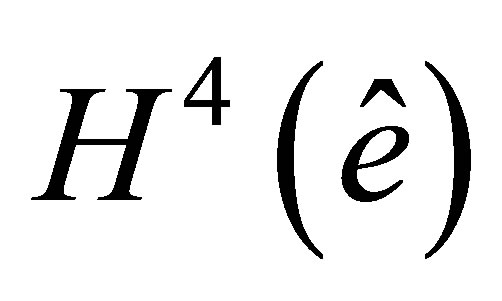 is continuously embedded into
is continuously embedded into 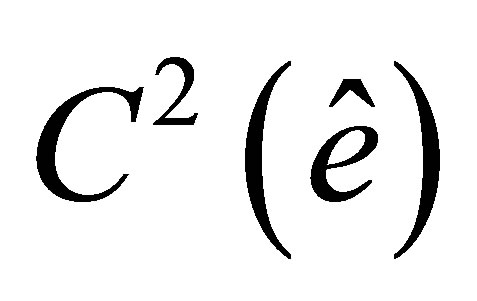 [20], hence,
[20], hence, . Thus, we can construct its interpolant
. Thus, we can construct its interpolant 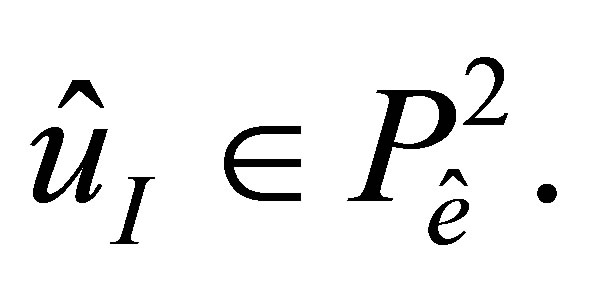 Denote by
Denote by  the number of degrees of freedom related to a node
the number of degrees of freedom related to a node 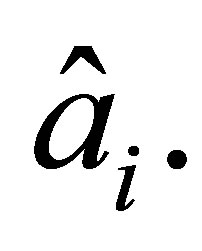 We have
We have

Theorem 1. Let 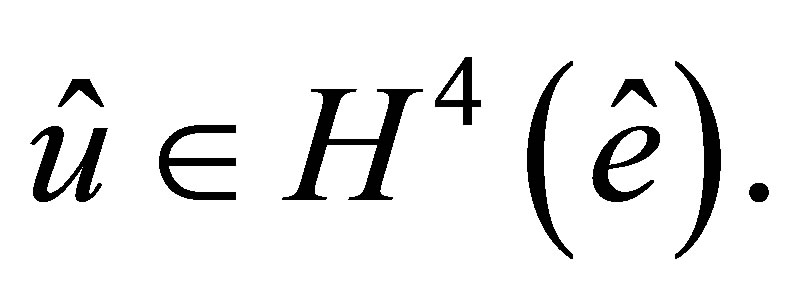 Then for any integer
Then for any integer 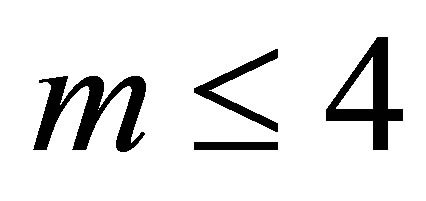 we have the estimate
we have the estimate
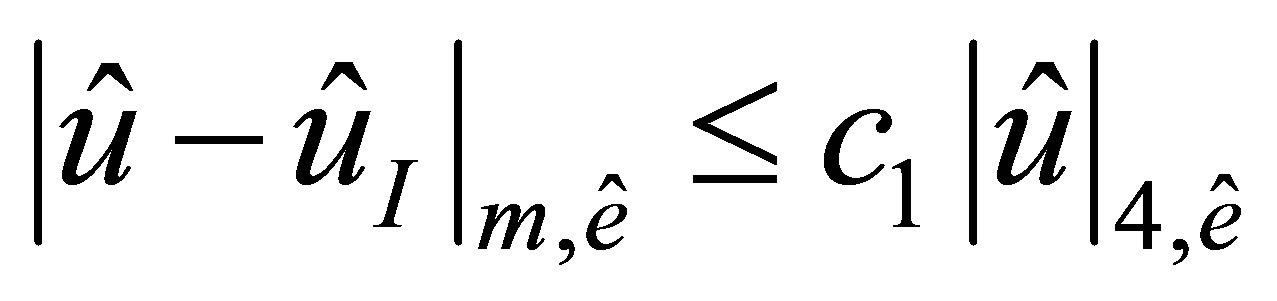 (6)
(6)
with constant  independent of
independent of 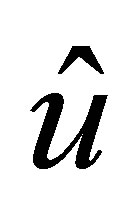 (and
(and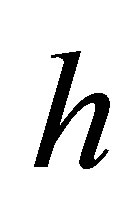 ).
).
Proof. The maximal order of partial derivatives equals 2 in the definition of the set 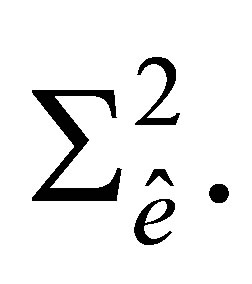 As mentioned above, the space
As mentioned above, the space  is embedded into
is embedded into 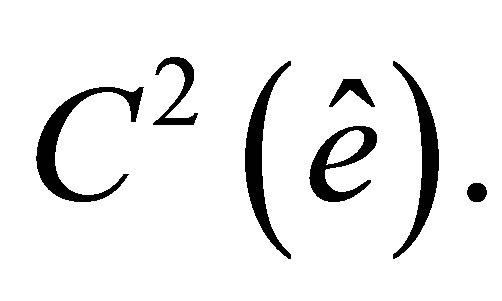 Besides, from (3) it follows that
Besides, from (3) it follows that 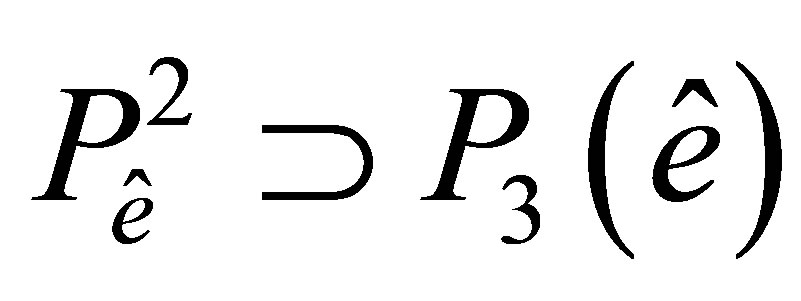 where
where 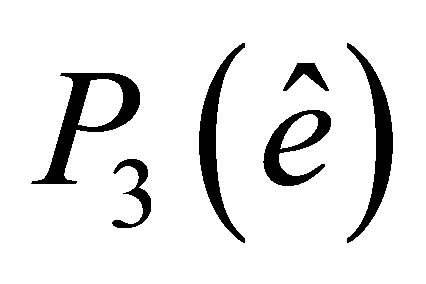 is the space of polynomials of degree no more than 3.
is the space of polynomials of degree no more than 3.
Thus, all the hypotheses of the Theorem 3.1.5 in [12] are fulfilled, which implies the estimate (6). ,
4. Combination of Rectangular and Triangular Elements
Let  be an arbitrary triangular element (Figure 3) with vertices
be an arbitrary triangular element (Figure 3) with vertices 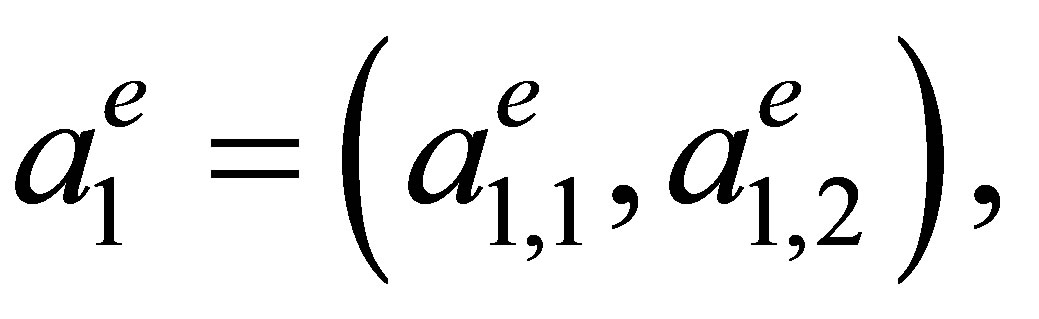

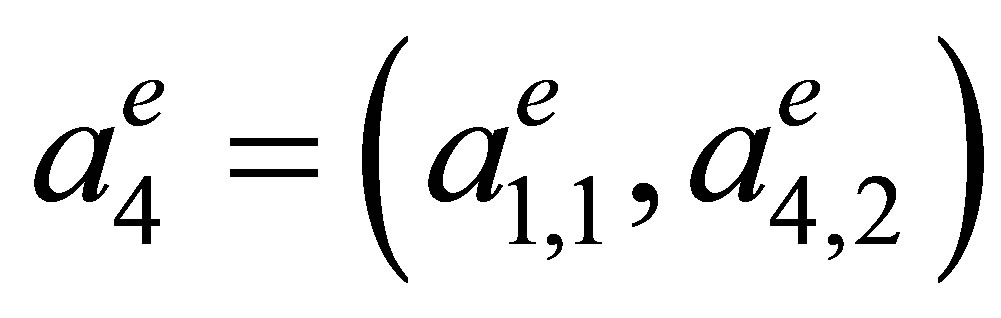 and side lengths
and side lengths 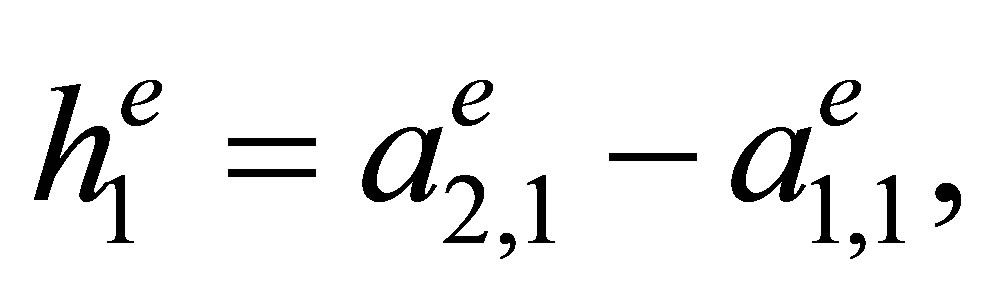
 The affine mapping
The affine mapping 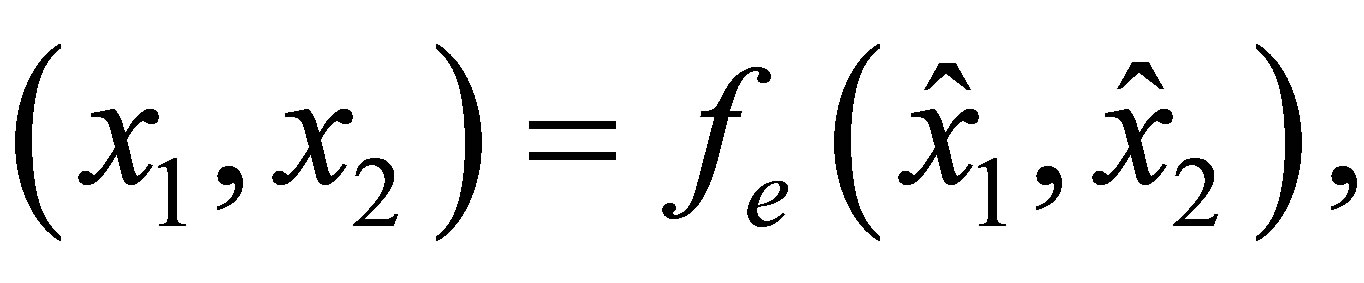 that maps the «reference» element
that maps the «reference» element  into е, has the form
into е, has the form
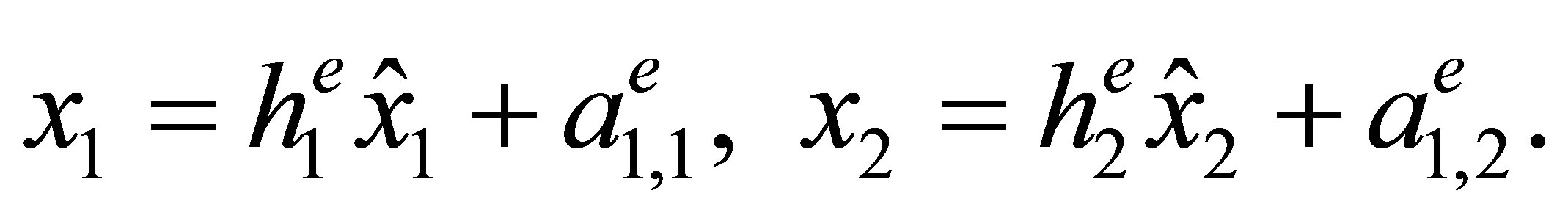 (7)
(7)
We specify the space 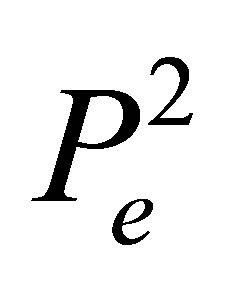 of functions and the set
of functions and the set  of degrees of freedom as follows:
of degrees of freedom as follows:
 (8)
(8)
The Lagrange basis in 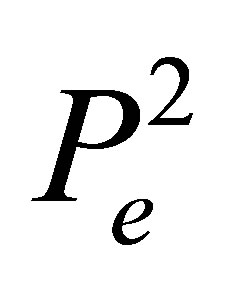 consists of the functions
consists of the functions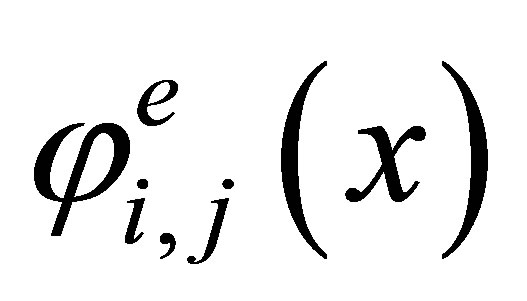 , where
, where  for i = 1,2,4 and j = 1 for i = 3 being the images of the basis (5) under the mapping (7) and satisfying the condition
for i = 1,2,4 and j = 1 for i = 3 being the images of the basis (5) under the mapping (7) and satisfying the condition
 (9)
(9)
Thus, the triple  is a finite element that is affinely equivalent to the «reference» element
is a finite element that is affinely equivalent to the «reference» element  [12].
[12].
Now denote the set of all nodes of the elements 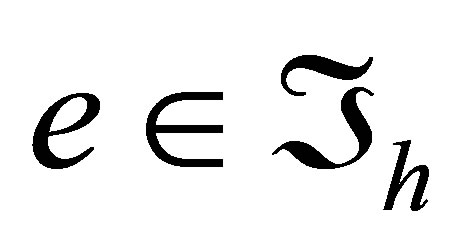 by
by 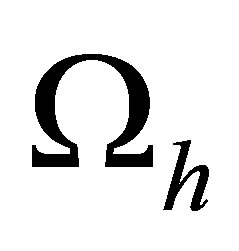 and number them from 1 to
and number them from 1 to 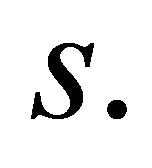 With each node
With each node 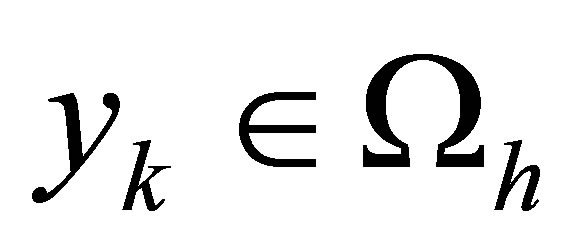 we associate the number
we associate the number 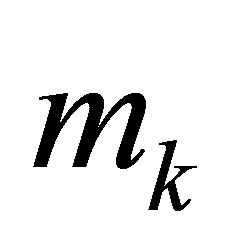 equal
equal
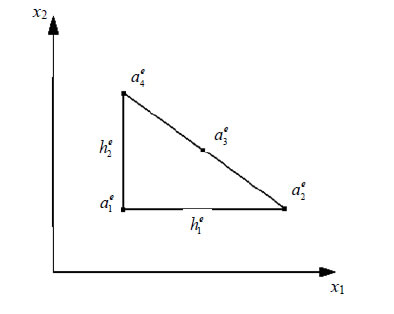
Figure 3. A triangular cell .
.
to the number of degrees of freedom related to this node. Observe that  is occurred when the node
is occurred when the node 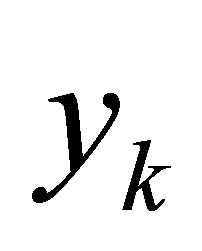 is the midpoint of the side of a triangular element being a part of the boundary
is the midpoint of the side of a triangular element being a part of the boundary 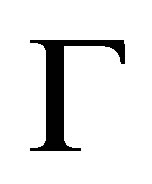 and
and 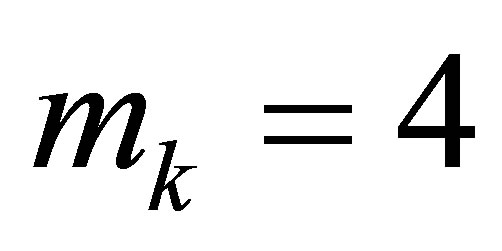 for all remaining nodes of
for all remaining nodes of 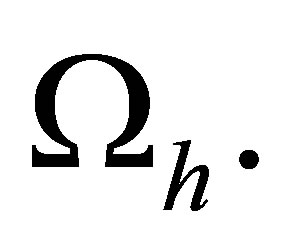
This is the global numbering of nodes. We also introduce the local numbering. The couple 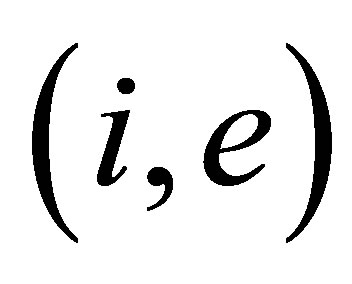 is assumed to be a local number of the node
is assumed to be a local number of the node  of an element
of an element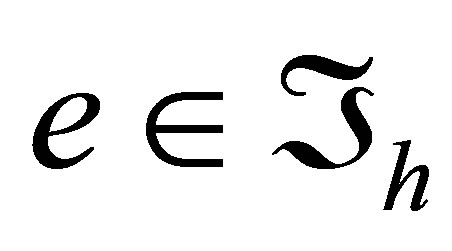 . To any local number
. To any local number 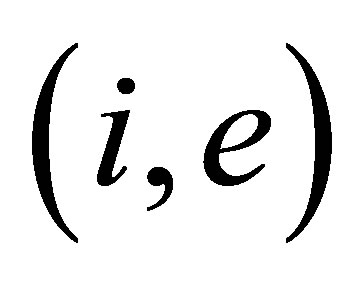 there corresponds one and only one global number
there corresponds one and only one global number  hence, we can introduce the function
hence, we can introduce the function  so that
so that  In addition, for an element
In addition, for an element  we denote the local analogue of the parameter
we denote the local analogue of the parameter  by
by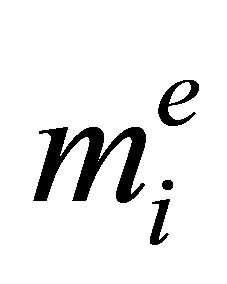 , i.e.,
, i.e.,  for
for 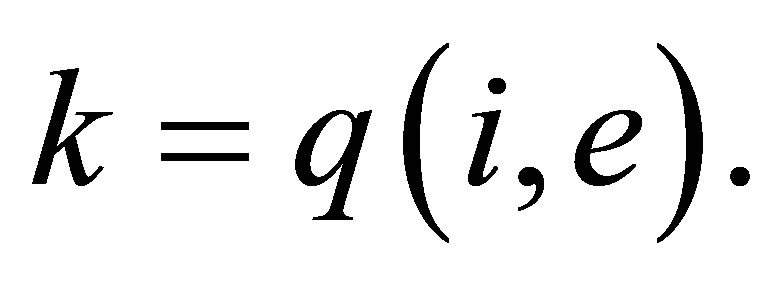
At each node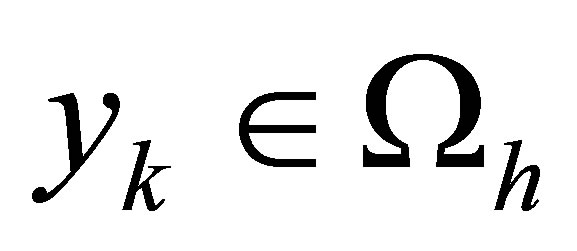 ,
, 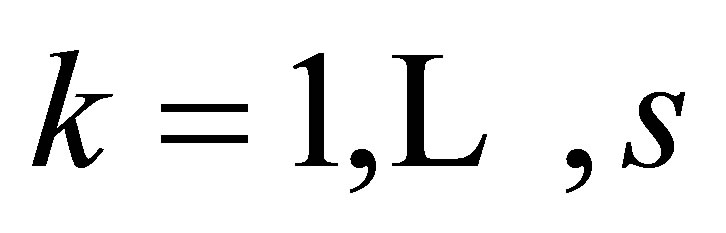 , we specify
, we specify 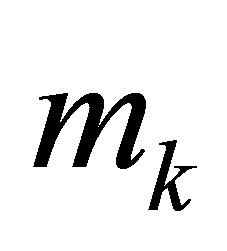 numbers
numbers  Construct the function
Construct the function 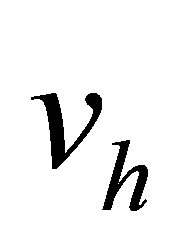 defined on
defined on  such that
such that 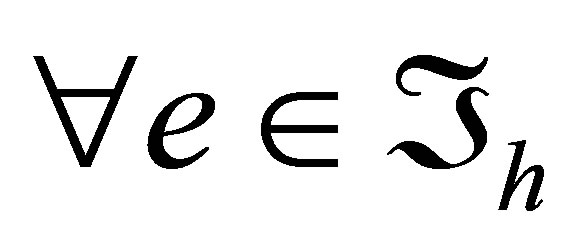
 (10)
(10)
By the construction, the function 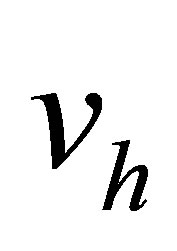 is uniquely defined on each
is uniquely defined on each . Put
. Put

Then  for any
for any 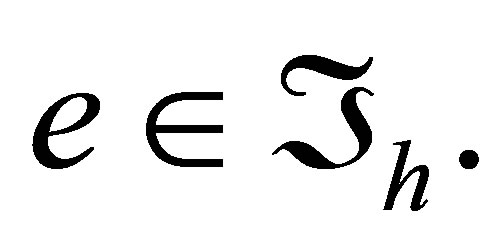
Lemma 2. The function  defined by the relation (10) belongs to
defined by the relation (10) belongs to 
Proof. The BFS-rectangles are elements of the class  i.e., the function
i.e., the function 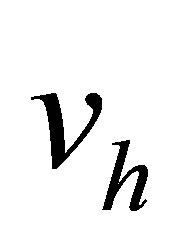 and its first-order derivatives are continuous on the sides common for two elements of this type [10].
and its first-order derivatives are continuous on the sides common for two elements of this type [10].
Now let  be an arbitrary triangular cell and
be an arbitrary triangular cell and 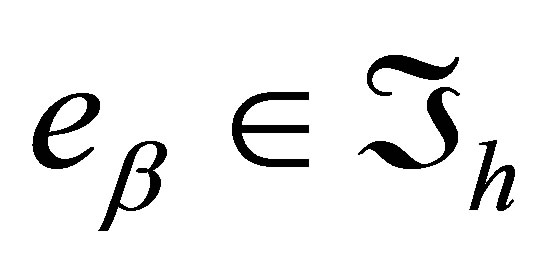 be a rectangular cell that has a common side
be a rectangular cell that has a common side 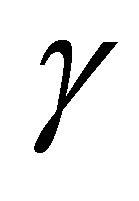 with
with 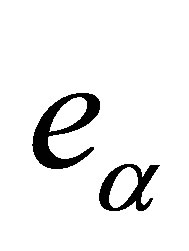 (Figure 4). Because of construction, the values of the nodal parameters of the functions
(Figure 4). Because of construction, the values of the nodal parameters of the functions  and
and 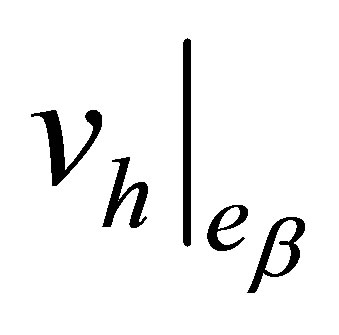 on
on  are equal. In addition, the traces of these functions and their first-order derivatives with respect to
are equal. In addition, the traces of these functions and their first-order derivatives with respect to  on
on 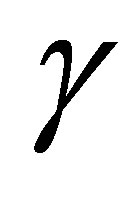 are polynomials of degree 3 in
are polynomials of degree 3 in 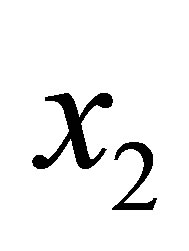 and are uniquely defined by the sets of nodal parameters related to the side
and are uniquely defined by the sets of nodal parameters related to the side
 . Hence, the functions
. Hence, the functions 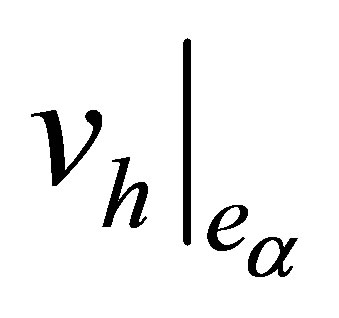 and
and 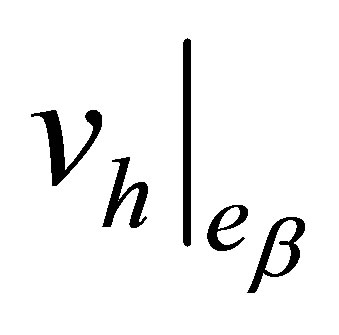 coincide on
coincide on
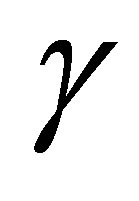 along with their first-order derivatives. ,
along with their first-order derivatives. ,
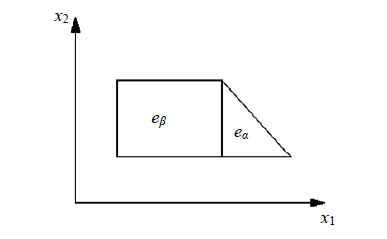
Figure 4. Two neighbouring elements of different types.
Corollary 1. 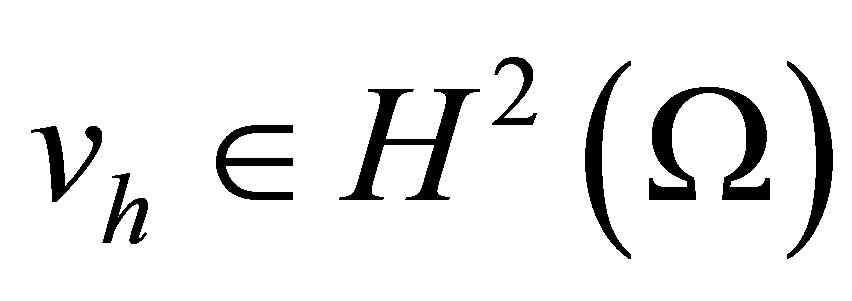 [12,21]. Thus, we can define the finite element space as follows:
[12,21]. Thus, we can define the finite element space as follows:

Let . Define its interpolant
. Define its interpolant  in the following way:
in the following way:
 (11)
(11)
With the help of the Theorem 1, the following estimate can be proved in the usual way (see, for instance, [12,14]).
Theorem 2. Assume that 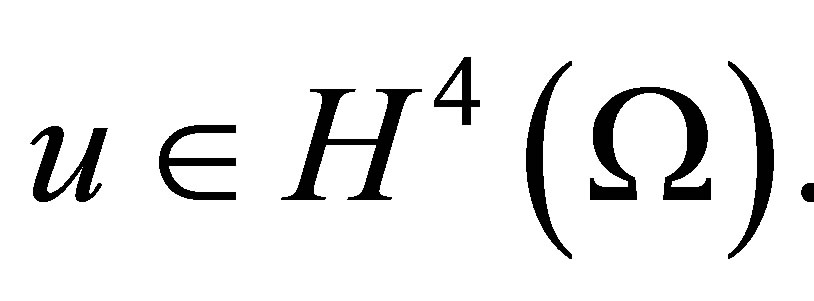 And let
And let 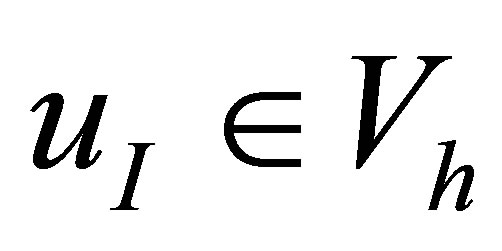 be its interpolant defined by (11). Then
be its interpolant defined by (11). Then

Here and later constants 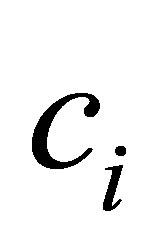 are independent of
are independent of 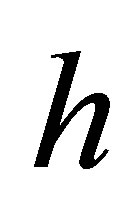 and
and 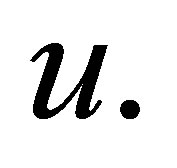
5. Numerical Example
We illustrate properties of the proposed finite elements by the following example. Let  be a right triangle with unit catheti (see Figure 5) and a boundary
be a right triangle with unit catheti (see Figure 5) and a boundary  Consider the problem
Consider the problem

with the right-hand side
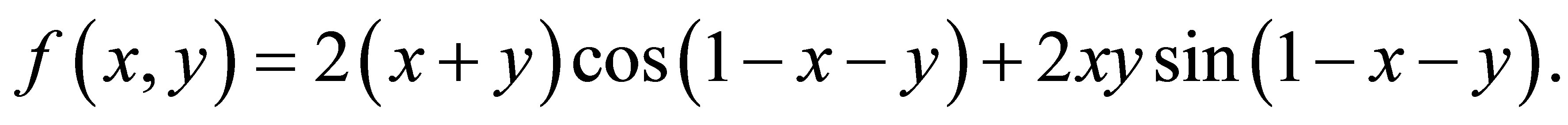
It has the exact solution

Subdivide the domain  into elementary squares (with triangles adjacent to the hupotenuse) by drawing two families of parallel straight lines
into elementary squares (with triangles adjacent to the hupotenuse) by drawing two families of parallel straight lines  and
and 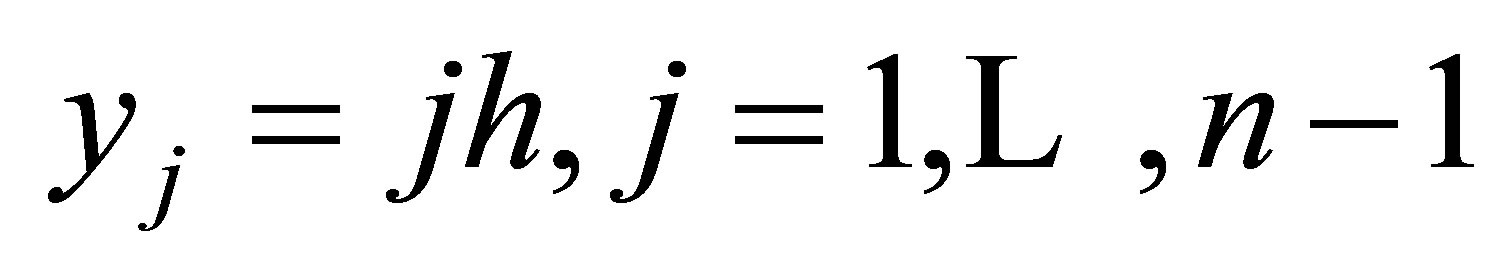 with mesh size
with mesh size 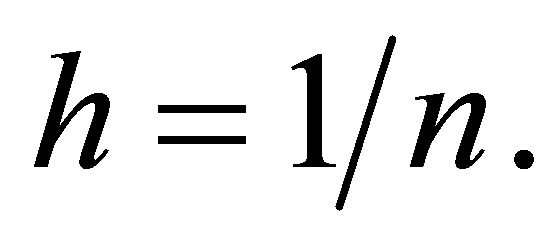
To compare accuracy with decreasing mesh size, we construct a system of linear algebraic equations of the finite element method with the BFS-elements on the elementary squares and the proposed elements on the
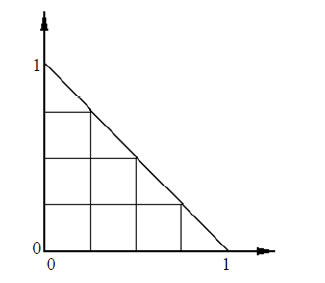
Figure 5. Domain Ω with initial triangulation.
triangles for  Since the exact solution is known, the difference
Since the exact solution is known, the difference  between exact and approximate solutions can be expressed in the explicit form. As a result, we have the following accuracy.
between exact and approximate solutions can be expressed in the explicit form. As a result, we have the following accuracy.
Theoretically, in the finite element method we have the estimate [12,14]

Combining it with the estimate in Theorem 2, we arrive at the following error estimate for an approximate solution:
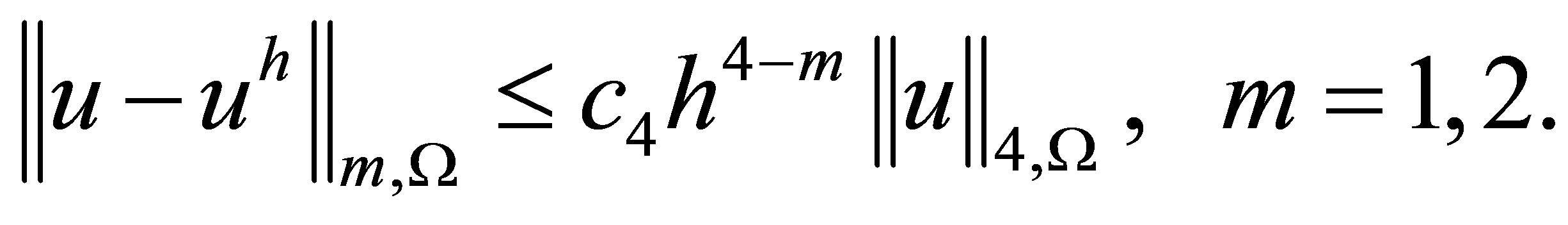 (12)
(12)
Comparing the last two results in Table 1, observe that they are close to the asymptotic values 4 and 3, respectively.
6. Summary and Further Implementations
Thus, the use of the proposed triangular finite elements only near a boundary extends the field of application of the BFS-elements at least for second order equations. In its turn, an approximate solution is of the class  enabling one to calculate a residual directly and considerably simplifies a posteriori accuracy estimates for an approximate solution.
enabling one to calculate a residual directly and considerably simplifies a posteriori accuracy estimates for an approximate solution.
In principle, to achieve the same order accuracy, instead of the BFS-elements, one can use the Lagrange bicubic elements on rectangles and the Lagrange elements of degree three on triangles. But in this case a general advantage of Hermite finite elements in comparison with Lagrange ones makes itself evident in the number of unknowns of a discrete system. In particular, Table 2 shows the number of degrees of freedom for an approximate solution which is equal to the number of unknowns and the number of equations in a discrete system of linear algebraic equations for the example from the above section.

Table 1. Accuracy of an approximate solution.

Table 2. The numbers of degrees of freedom for an approximate solution.

Figure 6. A “hanging” node b.
Observing a considerable gain in the number of unknowns, with the further refinement of triangulation, the number of unknowns (and equations) asymptotically tends to the ratio of 4:9 in favour of Hermite elements.
Now we notice an apparent inconvenience and show a way to overcome it that is also useful for nonconforming grid refinement. The triangulation shown in Figure 1 is constructed by adjusting cells of a rectangular grid in the  - and
- and  -directions. It imposes restrictions on the ratio of steps for a rectangular grid inside a domain. We show that the proposed triangular elements are sufficient to construct a conforming interpolant, generally speaking, on an “uncoordinated” grid without restriction on the ratio between steps.
-directions. It imposes restrictions on the ratio of steps for a rectangular grid inside a domain. We show that the proposed triangular elements are sufficient to construct a conforming interpolant, generally speaking, on an “uncoordinated” grid without restriction on the ratio between steps.
Considering a typical case shown in Figure 6, the node  is a so-called “hanging” node. At the algorithmic level, the challenge is solved as follows. For the degrees of freedom at the node b, instead of the corresponding variational equations for an approximate solution
is a so-called “hanging” node. At the algorithmic level, the challenge is solved as follows. For the degrees of freedom at the node b, instead of the corresponding variational equations for an approximate solution 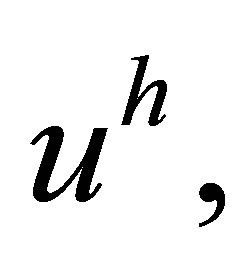 we write 4 linear algebraic equalities which express the quantities
we write 4 linear algebraic equalities which express the quantities 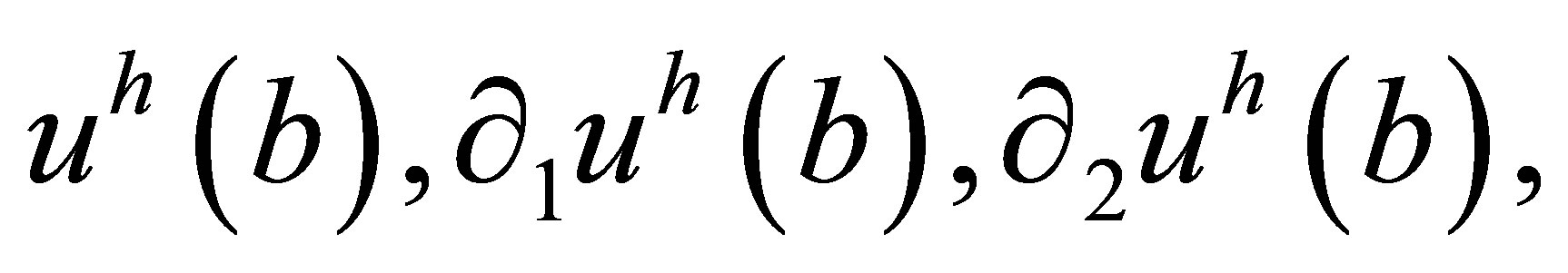 and
and 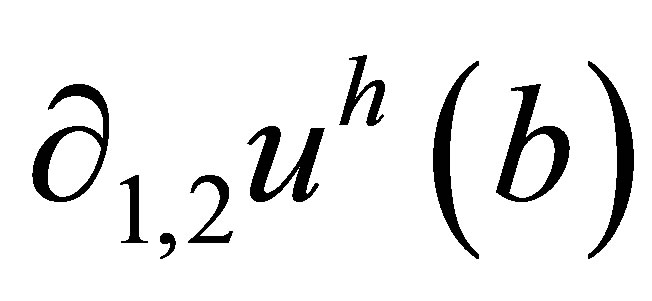 in terms of 16 degrees of freedom of the neighbouring rectangle
in terms of 16 degrees of freedom of the neighbouring rectangle 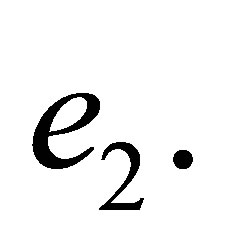 This trick ensures interelemental continuous differentiability of an interpolant between
This trick ensures interelemental continuous differentiability of an interpolant between  and
and 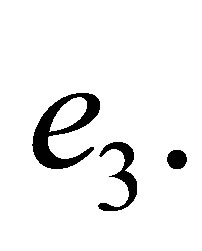 Thus in this case one again may implement proposed pair of elements in the frame of the conforming finite element method with estimate (12).
Thus in this case one again may implement proposed pair of elements in the frame of the conforming finite element method with estimate (12).
REFERENCES
- J. H. Argyris, I. Fried and D. W. Scharpf, “The TUBA Family of Plate Elements for the Matrix Displacement Method,” Journal of the Royal Aeronautical Society, Vol. 72, No. 692, 1968, pp. 701-709.
- K. Bell, “A Refined Triangular Plate Bending Element”, International Journal of Numerical Methods in Engineering, Vol. 1, No. 1, 1969, pp. 101-122. http://dx.doi.org/10.1002/nme.1620010108
- J. Morgan and L. R. Scott, “A Nodal Basis for C1 Piecewise Polynomials of Degree n,” Mathematics of Computation, Vol. 29, No. 131, 1975, pp. 736-740.
- R. W. Clough and J. L. Tocher, “Finite Element Stiffness Matrices for Analysis of Plates in Bending,” Proceedings of the Conference on Matrix Methods in Structural Mechanics, Wright-Patterson Air Force Base, Ohio, October 1965, pp. 515-545.
- P. Percell, “On Cubic and Quartic Clough-Tocher Finite Elements,” SIAM Journal on Numerical Analysis, Vol. 13, No. 1, 1976, pp. 100-103. http://dx.doi.org/10.1137/0713011
- J. Douglas Jr., T. Dupont, P. Percell and R. Scott, “A Family of C1 Finite Elements with Optimal Approximation Properties for Various Galerkin Methods for 2nd and 4th Order Problems”, RAIRO Analise Numérique, Vol. 13, No. 3, 1979, pp. 227-255.
- M. J. D. Powell and M. A. Sabin, “Piecewise Quadratic Approximations on Triangles,” ACM Transactions on Mathematical Software, Vol. 3-4, No. 4, 1977, pp. 316- 325. http://dx.doi.org/10.1145/355759.355761
- B. Fraeijs de Veubeke, “Bending and Stretching of Plates”, Proceedings of the Conference on Matrix Methods in Structural Mechanics, Wright-Patterson Air Force Base, Ohio, October 1965, pp. 863-886.
- B. Fraeijs de Veubeke, “A Conforming Finite Element for Plate Bending,” In: J. C. Zienkievicz and G. S. Holister, Eds., Stree Analysis, Wiley, New York, 1965, pp. 145- 197.
- F. K. Bogner, R. L. Fox and L. A. Schmit, “The Generation of Interelement Compatible Stiffness and Mass Matrices by the Use of Interpolation Formulas,” Proceedings of the Conference on Matrix Methods in Structural Mechanics, Wright-Patterson Air Force Base, Ohio, October 1965, pp. 397-444.
- S. Zhang, “On the full C1-Qk Finite Element Spaces on Rectangles and Cuboids,” Advances in Applied Mathematics and Mechanics, Vol. 2, No. 6, 2010, pp. 701-721.
- P. G. Ciarlet, “The Finite Element Method for Elliptic Problems,” North-Holland, Amsterdam, 1978.
- Z. C. Li and N. Yan, “New Error Estimates of Bi-Cubic Hermite Finite Element Methods for Biharmonic Equations,” Journal of Computational and Applied Mathematics, Vol. 142, No. 2, 2002, pp. 251-285. http://dx.doi.org/10.1016/S0377-0427(01)00494-0
- S. C. Brenner and L. R. Scott, “The Mathematical Theory of Finite Element Methods,” Springer-Verlag, New York, 1994. http://dx.doi.org/10.1007/978-1-4757-4338-8
- B. M. Irons, “A Conforming Quadratic Triangular Element for Plate Bending,” International Journal for Numerical Methods in Engineering, Vol. 1, No. 1, 1969, pp. 101-122.
- D. L. Logan, “A First Course of Finite Element Method,” SI Edition, 2011.
- J. Blaauwendraad, “Plates and FEM: Surprises and Pitfalls,” Springer, New York, 2010. http://dx.doi.org/10.1007/978-90-481-3596-7
- J. Zhao, “Convergence of Vand F-cycle Multigrid Methods for Biharmonic Problem Using the HsiehClough-Tocher Element,” Numerical Methods for Partial Differential Equations, Vol. 21, No. 3, 2005, pp. 451-471. http://dx.doi.org/10.1002/num.20048
- J. Petera and J. F. T. Pittman, “Isoparametric Hermite elements,” Intenational Journal for Numerical Methods in Engineering, Vol. 37, No. 20, 1994, pp. 3480-3519.
- R. A. Adams and J. J. F. Fournier, “Sobolev Spaces,” Academic Press, New York, 2003.
- Z. Chen and H. Wu, “Selected Topics in Finite Element Methods,” Science Press, Beijing, 2010.

