Applied Mathematics
Vol.4 No.12(2013), Article ID:39801,8 pages DOI:10.4236/am.2013.412220
Hybrid Adaptive Synchronization of Hyperchaotic Systems with Fully Unknown Parameters
Mathematics Department, Faculty of Science, University of Ha’il, Ha’il, KSA
Email: sawalha_moh@yahoo.com
Copyright © 2013 M. Mossa Al-sawalha. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received October 1, 2013; revised November 1, 2013; accepted November 8, 2013
Keywords: Hybrid Synchronization; Adaptive Control; Unknown Parameters; Hyperchaotic System
ABSTRACT
In this paper, an adaptive control scheme is developed to study the hybrid synchronization behavior between two identical and different hyperchaotic systems with unknown parameters. This adaptive hybrid synchronization controller is designed based on Lyapunov stability theory and an analytic expression of the controller with its adaptive laws of parameters is shown. The adaptive hybrid synchronization between two identical systems (hyperchaotic Chen system) and different systems (hyperchaotic Lorenz and hyperchaotic Lű systems) are taken as two illustrative examples to show the effectiveness of the proposed method. Theoretical analysis and numerical simulations are shown to verify the results.
1. Introduction
Chaos is an omnipresent phenomenon. Scientists who understand its existence have been struggling to control chaos to our benefit. There is a great need to control the chaotic systems as chaos theory plays an important role in industrial applications particularly in chemical reactions, biological systems, information processing and secure communications [1-3]. Many scientists who are interested in this field have struggled to achieve the synchronization or anti-synchronization of different hyperchaotic systems. Therefore due to its complexity and applications, a wide variety of approaches have been proposed for the synchronization or anti-synchronization of hyperchaotic systems. The types of synchronization used so far include generalized active control [4-8], nonlinear control [9,10], and adaptive control [11-19].
The co-existence of synchronization and anti-synchronization, known as hybrid synchronization, has good application prospects in digital communications. Therefore it attracted a lot of attention in recent years. In hybrid synchronization scheme, one part of the system is anti-synchronized and the others are completely synchronized so that complete synchronization and anti-synchronization co-exist in the system. The co-existence of CS and AS may enhance security in communication and chaotic encryption schemes. Li [20] studied full state hybrid projective synchronization behavior in multiscroll chaotic systems in symmetrical coordinate subspace. Xie, Chen and Bolt [21], through numerical studies show that an arbitrary signal can be synchronized by hybrid chaotic system and then that particular signal can then be stored for password and message identification. They further identify potential applications in information storage, message identification and certain types of secure signal and image communications.
Zhang and Lű [22] introduce a new type of hybrid synchronization called full state hybrid log projective synchronization and apply it to the Rossler systems and the hyperchaotic Lorenz system to numerically verify their results. Similarly Chen, Chen and Lin [23] achieve hybrid synchronization in Chin-Lee system using both linear and non-linear control schemes. Recently Sun et al. [24] analyze the hybrid synchronization of two coupled complex networks using linear feedback and adaptive feedback control methods. They derive a criterion for the hybrid synchronization of the two complex networks and show that under suitable conditions two complex networks can realize hybrid synchronization. More recently, Vaidyanathan and Rasappan [25] investigate the hybrid chaos synchronization of hyperchaotic Qi and Jia systems using active nonlinear control. The idea of the aforementioned type of hybrid synchronization of chaotic systems deals with systems with known parameters. However in practical engineering situations, parameters are probably unknown and may change from time to time. Therefore, there is a vital need to effectively hybridsynchronize two chaotic systems (identical and different) with unknown parameters. This is typically important in theoretical research as well as practical applications. Among the aforementioned methods, adaptive control [11-19] is an effective option for achieving the synchronization of chaotic systems with fully unknown parameters. Therefore motivated by this, we study the hybrid synchronization of two identical and two different hyperchaotic systems with fully unknown parameters. The rest of the paper is organized as follows. In Section 2, we present a novel adaptive hybrid synchronization scheme with a parameter update law and give a brief description of the systems. In Sections 3 and 4, we present the hyperchaos hybrid synchronization between two identical and different hyper chaotic systems via adaptive control. Conclusions are given in Section 5.
2. Problem Formulation and Systems Description
In the first part of this section, we set up the problem and present novel adaptive hybrid synchronization scheme with parameter update law. By using Lyapunov stability theory we show the co-existence of hybrid synchronization between two systems described below. In the second part of this section we briefly describe the two systems used for further analysis.
2.1. Hybrid Synchronization of Chaotic Systems
Consider the master chaotic system in the form of
 (1)
(1)
where 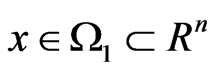 is the state vector,
is the state vector, 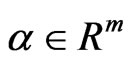 is the unknown constant parameter vector of the system,
is the unknown constant parameter vector of the system,  is an
is an 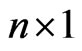 matrix,
matrix, 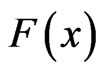 is an
is an 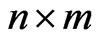 matrix whose elements
matrix whose elements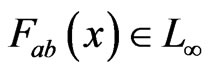 . The slave system is assumed by:
. The slave system is assumed by:
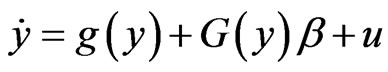 (2)
(2)
where  is the state vector,
is the state vector, 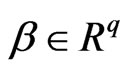 is the unknown constant parameter vector of the system
is the unknown constant parameter vector of the system 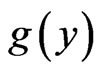 is an
is an 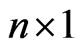 matrix,
matrix, 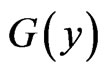 is an
is an  matrix whose elements
matrix whose elements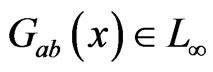 , and
, and 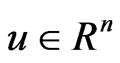 is control input vector. If we divide the master and the slave systems into two parts, then system (1) can be written as:
is control input vector. If we divide the master and the slave systems into two parts, then system (1) can be written as:
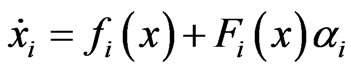 (3)
(3)
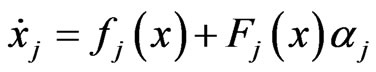 (4)
(4)
and the slave system (2) can be written as
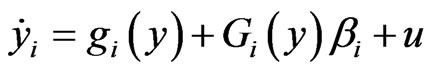 (5)
(5)
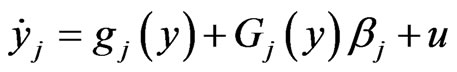 (6)
(6)
Let 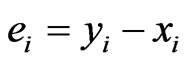 and
and 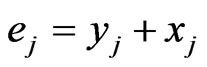 be the synchronization and the anti–synchronization error vector’s respectively. Our goal is to design a controller
be the synchronization and the anti–synchronization error vector’s respectively. Our goal is to design a controller 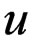 such that the trajectory of the response system (5)-(6) with initial conditions
such that the trajectory of the response system (5)-(6) with initial conditions 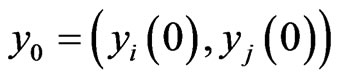 can asymptotically approach the drive system, (3)-(4), with initial condition
can asymptotically approach the drive system, (3)-(4), with initial condition 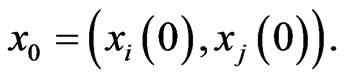 And finally implement the hybrid synchronization such that,
And finally implement the hybrid synchronization such that, 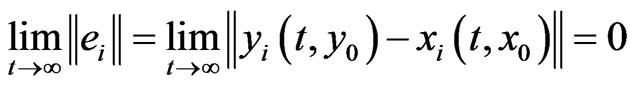 and the anti-synchronization such that
and the anti-synchronization such that
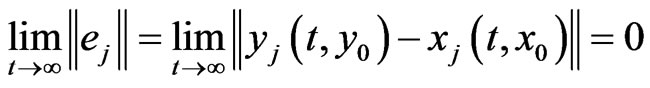
where 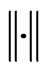 is the Euclidean norm.
is the Euclidean norm.
2.2. Adaptive Hybrid Synchronization Controller Design
Theorem: If the nonlinear control 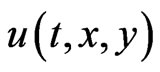 is selected as:
is selected as:

and adaptive laws of parameters are taken as:
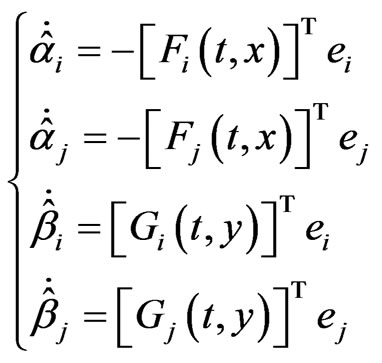
then the response system (5)-(6) can synchronize and anti-synchronize the drive system (3)-(4) globally and asymptotically, where 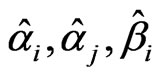 and
and 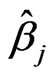 are respecttively, estimations of the unknown parameters
are respecttively, estimations of the unknown parameters  and
and 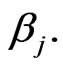
Proof: From Equations (3)-(6), we get the error dynamical systems as follows:
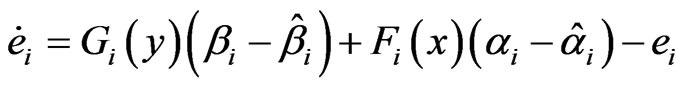 (7)
(7)
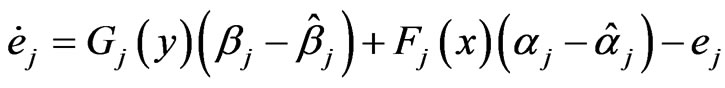 (8)
(8)
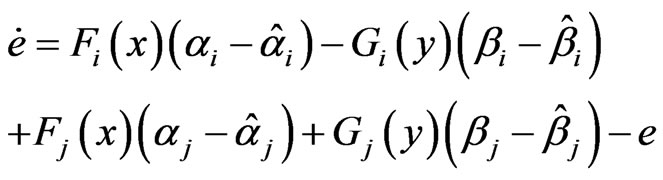 (9)
(9)
where 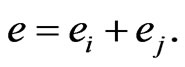
Let  and
and 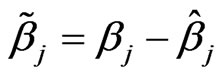 .
.
If a Lyapunov function candidate is chosen as
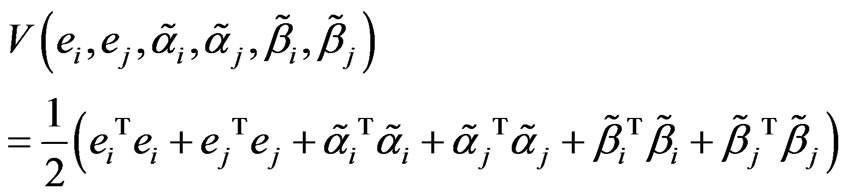 (10)
(10)
The time derivative of V along the error dynamical system is given by:
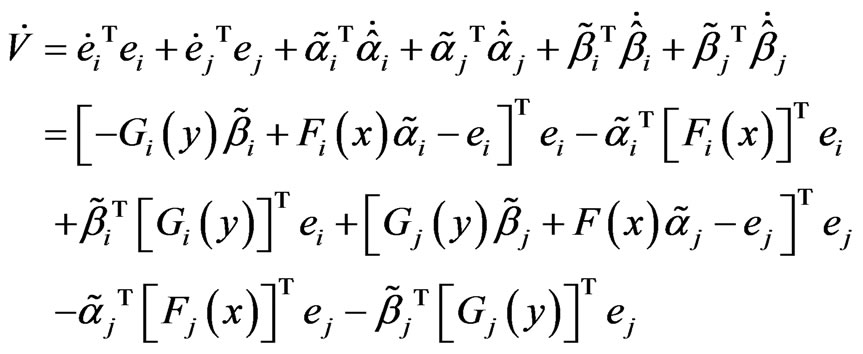 (11)
(11)
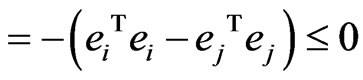 (12)
(12)
Since 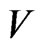 is positive definite, and
is positive definite, and 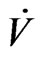 is negative semi-definite, it follows that from the fact that
is negative semi-definite, it follows that from the fact that
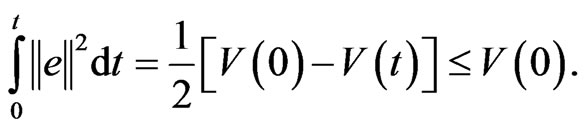
It can easily be seen that 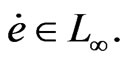 From Equation (9) have
From Equation (9) have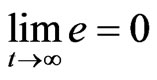 . Thus, by Barbalat’s lemma, we have
. Thus, by Barbalat’s lemma, we have 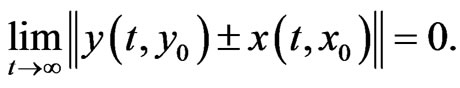 Thus the response system (2) can be synchronized and anti-synchronized the drive system (1) globally and asymptotically. This completes the proof.
Thus the response system (2) can be synchronized and anti-synchronized the drive system (1) globally and asymptotically. This completes the proof.
2.3. Systems Description
The hyperchaotic Chen system [26,27] is given by:
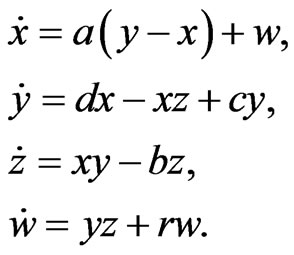 (13)
(13)
where 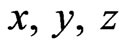 and
and 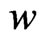 are state variables, and
are state variables, and 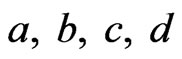 , and
, and 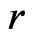 are real constants. When
are real constants. When 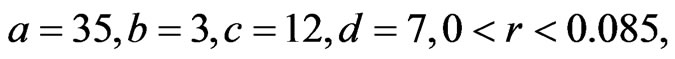 system (13) is chaotic, when
system (13) is chaotic, when 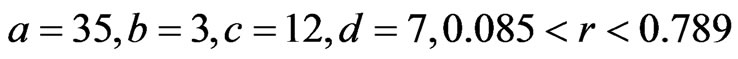 , system (13) is hyperchaotic.
, system (13) is hyperchaotic.
The hyperchaotic Lorenz system [28,29] is described by
 (14)
(14)
where , and
, and 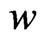 are state variables,
are state variables, 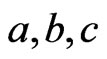 and
and 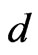 are real constants. When
are real constants. When  and
and 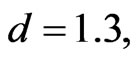 system (14) has hyperchaotic attractor.
system (14) has hyperchaotic attractor.
The hyperchaotic Lű system [30] is described by:
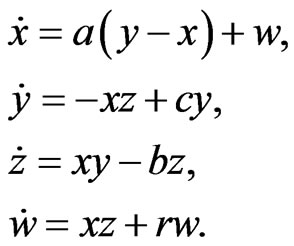 (15)
(15)
where  and
and 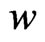 are state variables,
are state variables, 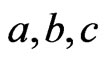 and
and  are real constants. When
are real constants. When 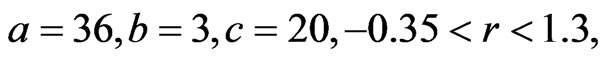 system (15) has hyperchaotic attractor.
system (15) has hyperchaotic attractor.
3. Adaptive Hybrid Synchronization of Two Identical Hyperchaotic Systems with Unknown Parameters
In order to observe the efficacy of our proposed method, we used two hyperchaotic Chen systems where the master system is denoted with the subscript 1 and the response system having identical equations denoted by the subscript 2. The two systems are defined below.
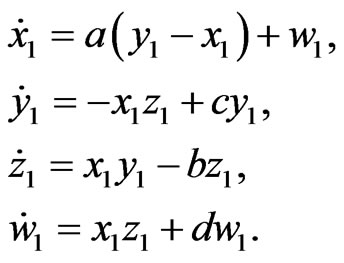 (16)
(16)
and
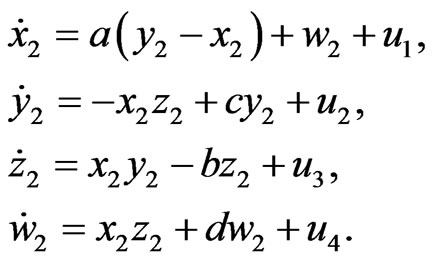 (17)
(17)
where  are four control functions to be designed. For the hybrid synchronization, we define the state errors between the response system that is to be controlled and the controlling drive system as
are four control functions to be designed. For the hybrid synchronization, we define the state errors between the response system that is to be controlled and the controlling drive system as 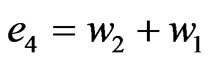
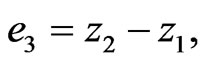
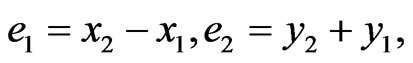 . The error system is given by
. The error system is given by
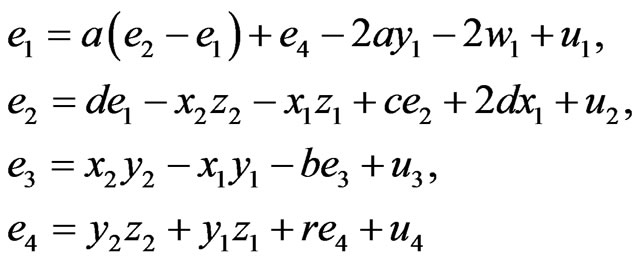 (18)
(18)
Now our goal is to find proper control functions 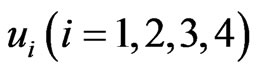 and parameter update rule, such that system (17) globally hybrid synchronizes system (16) asymptotically. i.e.,
and parameter update rule, such that system (17) globally hybrid synchronizes system (16) asymptotically. i.e., 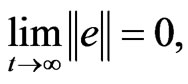 where
where
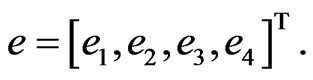 If the two systems are without controls
If the two systems are without controls 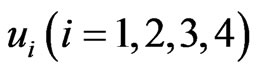 and the initial condition is:
and the initial condition is:
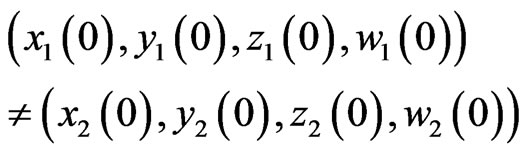
then the trajectories of the two systems will quickly separate each other and become irrelevant. However, when appropriate controls are applied the two systems will approach hybrid synchronization for any initial conditions. We shall propose the following adaptive control law for system (17).
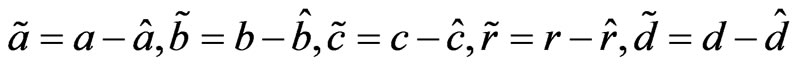
where 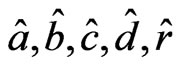 are the estimates of
are the estimates of  respectively. Now, let us choose a controller
respectively. Now, let us choose a controller 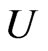 and parameters update law
and parameters update law 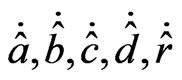 as follows:
as follows:
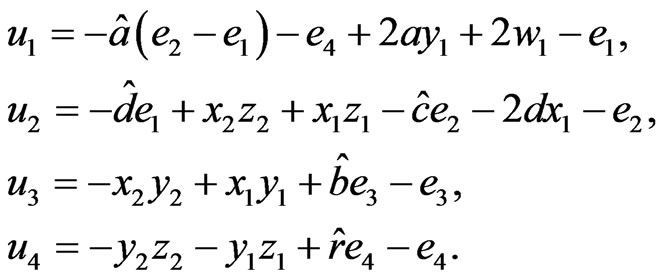 (19)
(19)
and the parameter update rule.
Consider the following Lyapunov function
 (20)
(20)
Consider the following Lyapunov function
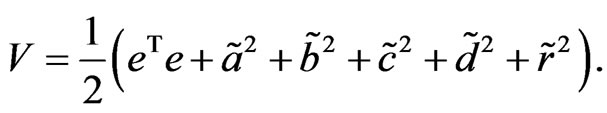
Then the time derivative of 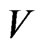 along the trajectories of Equation (18) is:
along the trajectories of Equation (18) is:
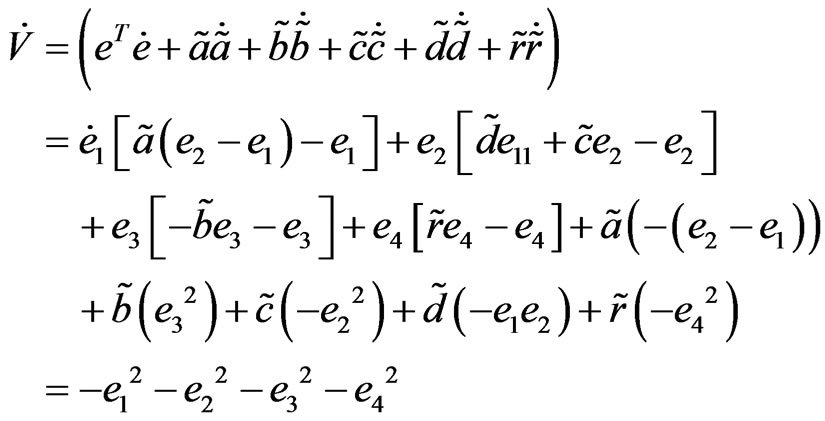 (21)
(21)
Since 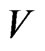 is positive definite function and
is positive definite function and  is negative definite function, it translates to
is negative definite function, it translates to  based on the Lyapunov stability theorem [31]. Therefore, the hyperchaotic Chen response system (17) is hybrid synchronized with hyperchaotic Chen drive system (16) with fully uncertain parameters under the adaptive controller (19) and the parameters update law (20).
based on the Lyapunov stability theorem [31]. Therefore, the hyperchaotic Chen response system (17) is hybrid synchronized with hyperchaotic Chen drive system (16) with fully uncertain parameters under the adaptive controller (19) and the parameters update law (20).
Numerical Simulations
To verify and demonstrate the effectiveness of the proposed method, we discuss the simulation results for hyperchaotic Chen system. In the numerical simulations, the fourth-order Runge-Kutta method is used to solve the systems with time step size 0.001. For these numerical simulations, we used the initial conditions, 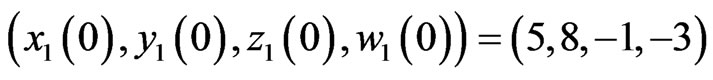 and
and 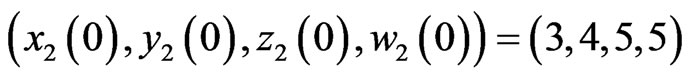 . Hence, the error system has the initial values
. Hence, the error system has the initial values 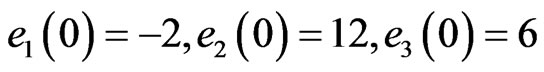 and
and 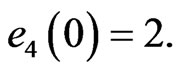 The unknown parameters are chosen as
The unknown parameters are chosen as  and
and 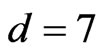 such that the hyperchaotic Chen system exhibits chaotic behavior. Hybrid synchronization of systems (16) and (17) via adaptive control laws (Equations (19) and (20)) with the initial estimated parameters
such that the hyperchaotic Chen system exhibits chaotic behavior. Hybrid synchronization of systems (16) and (17) via adaptive control laws (Equations (19) and (20)) with the initial estimated parameters 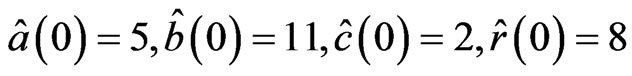 and
and  are shown in Figures 1 and 2. Figures 1(a) and (d) display state trajectories of drive system (16) and the response system (17). Figure 2(a) displays the hybrid synchronization errors between system (16) and (17). Figure 2(b) Shows that the estimates
are shown in Figures 1 and 2. Figures 1(a) and (d) display state trajectories of drive system (16) and the response system (17). Figure 2(a) displays the hybrid synchronization errors between system (16) and (17). Figure 2(b) Shows that the estimates  and
and 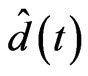 of the unknown parameters converges to
of the unknown parameters converges to 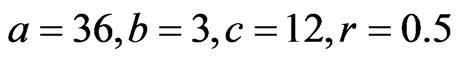 and
and 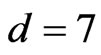 as
as 
4. Adaptive Hybrid Synchronization between Two Different Hyperchaotic Systems
In order to observe the hybrid synchronization behavior between hyperchaotic Lorenz system (15) and hyperchaotic Lű system (14), we assume that hyperchaotic Lorenz system with four unknown parameters is the drive system and hyperchaotic Lű system with four unknown parameters is the response system. The drive and response systems are defined as follows:
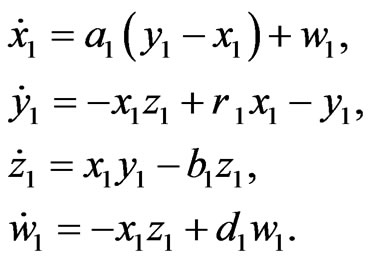
and
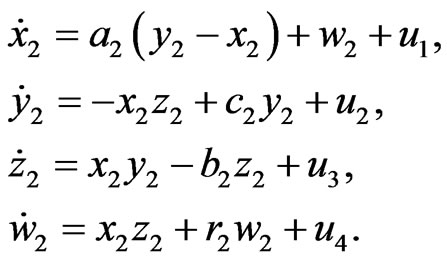 (23)
(23)
where 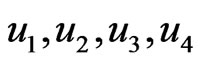 are four control functions to be designed. For the hybrid synchronization, we define the state errors between the response system that is to be controlled and the controlling drive system as
are four control functions to be designed. For the hybrid synchronization, we define the state errors between the response system that is to be controlled and the controlling drive system as 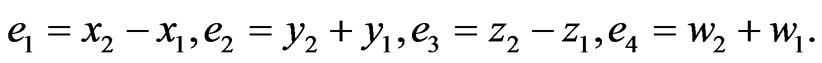
The error system is given by
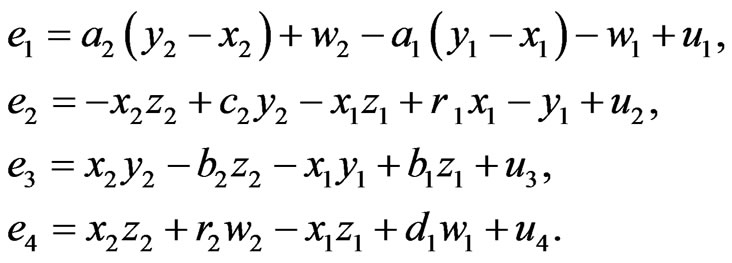 (24)
(24)
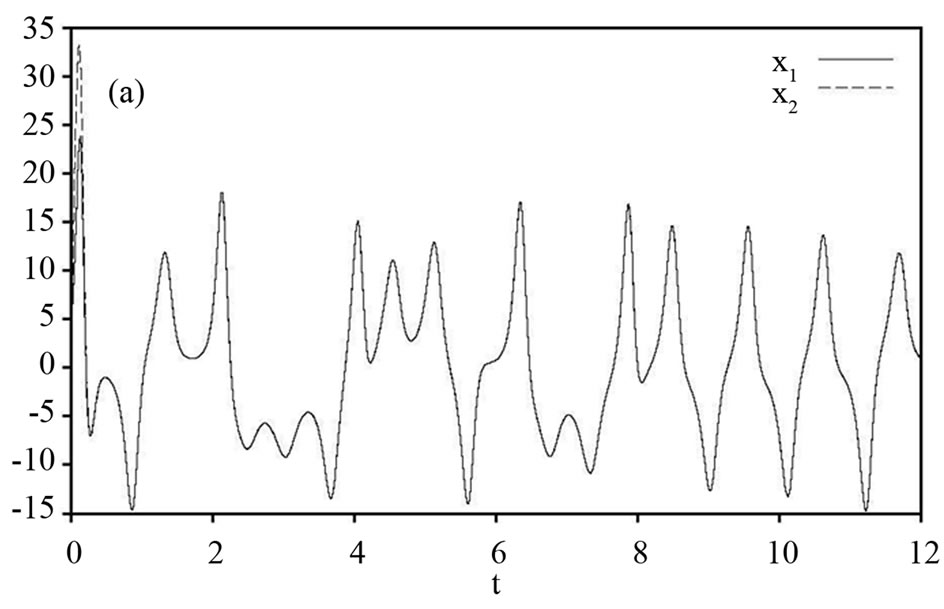
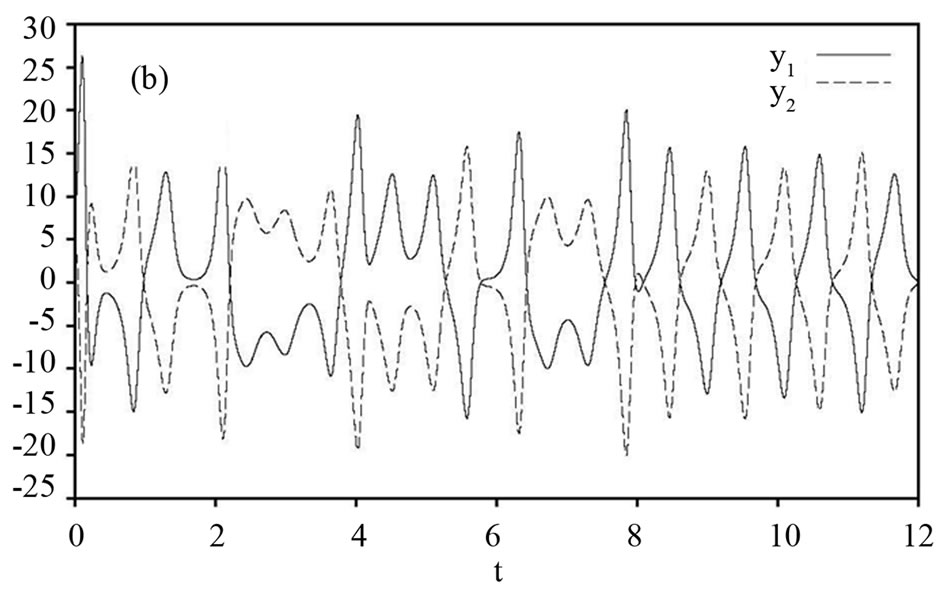
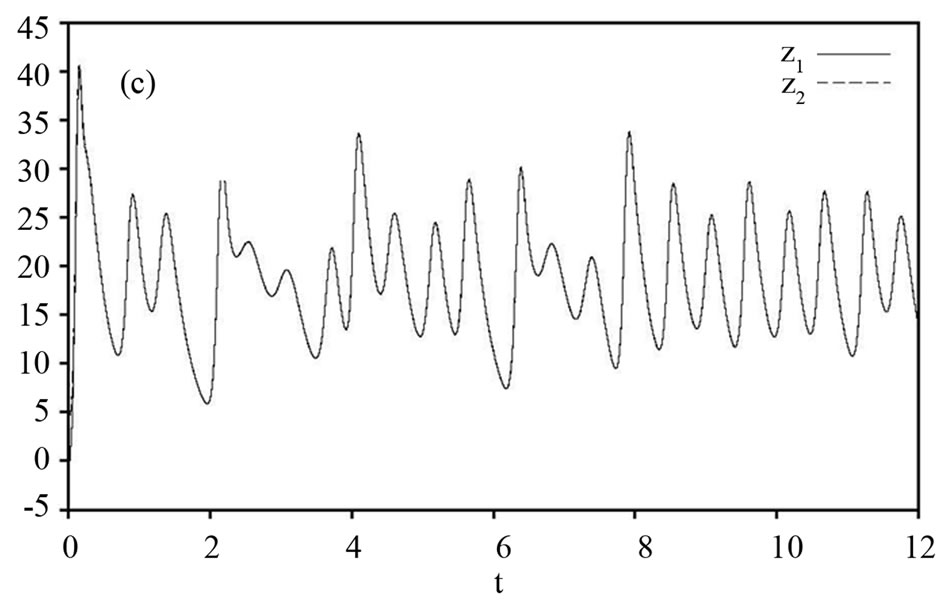
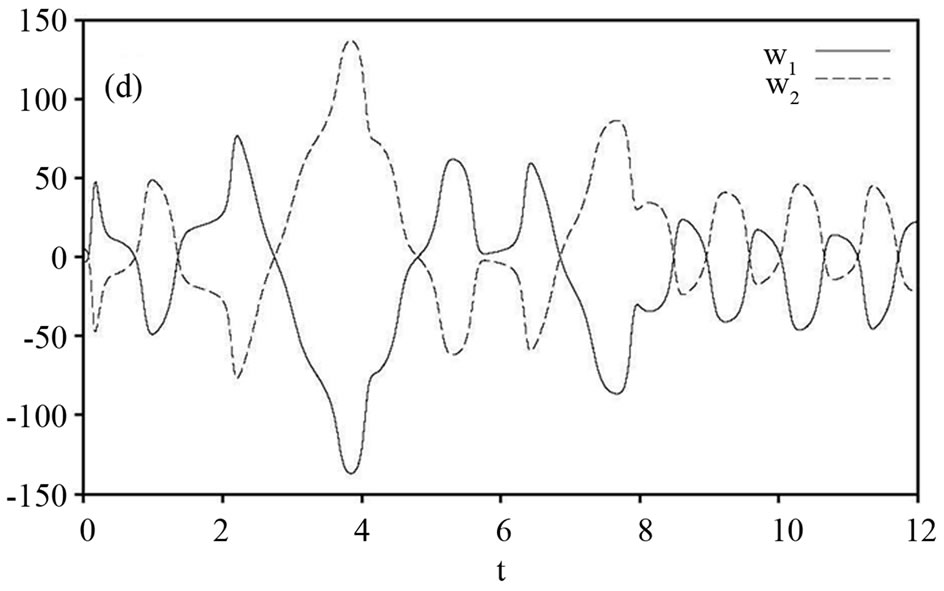
Figure 1. State trajectories of the drive system (16) and the response system (17). (a) Signals 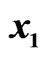 and
and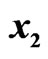 ; (b) Signals
; (b) Signals 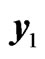 and
and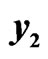 ; (c) Signals
; (c) Signals 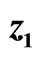 and
and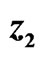 ; and (d) Signals
; and (d) Signals 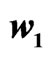 and
and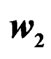 .
.
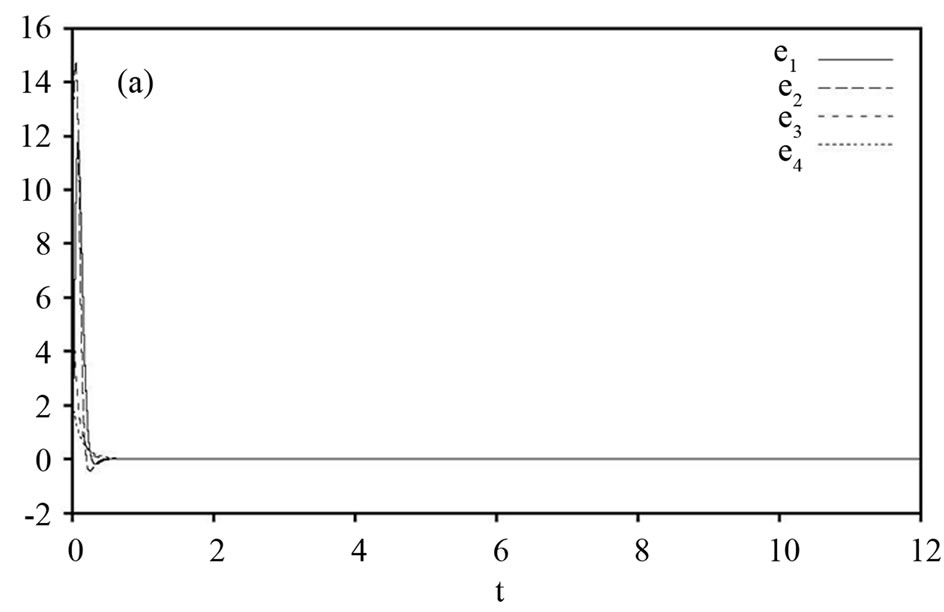
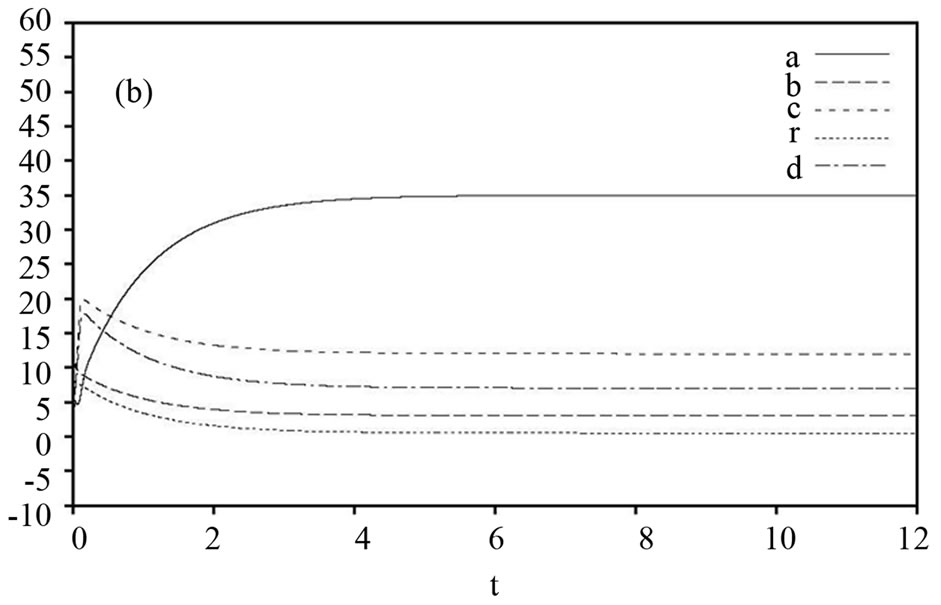
Figure 2. (a) Hybrid synchronization errors 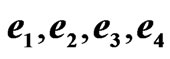 of the drive system (16) and the response system (17) with time
of the drive system (16) and the response system (17) with time ; (b) Changing parameters
; (b) Changing parameters 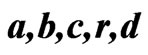 of the drive system (16) and the response system (17) with time
of the drive system (16) and the response system (17) with time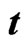 .
.
Now our goal is to find proper control functions 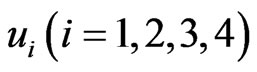 and parameter update rule, such that system (17) globally hybrid synchronizes system (16) asymptotically. i.e.
and parameter update rule, such that system (17) globally hybrid synchronizes system (16) asymptotically. i.e. 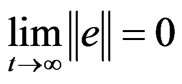 where
where
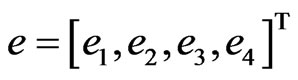 . If the two systems are without controls
. If the two systems are without controls 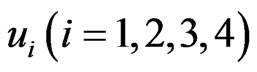 and the initial condition is
and the initial condition is
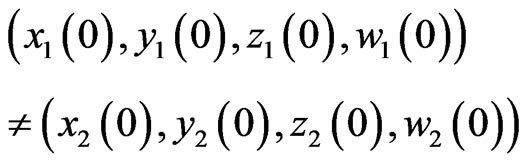
then the trajectories of the two systems will quickly separate each other and become irrelevant. However, when appropriate controls are applied the two systems will approach hybrid synchronization for any initial conditions. We shall propose the following adaptive control law for system (23). We define the parameters error 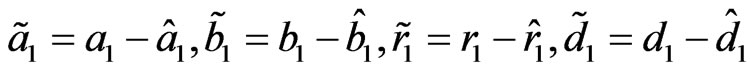 and
and
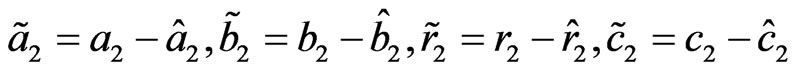 where
where
 and
and 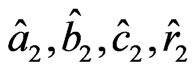 are the estimates of
are the estimates of 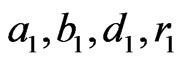 and
and 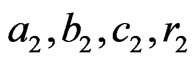 respectively. Now, let us choose a controller
respectively. Now, let us choose a controller 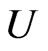 and parameters update law
and parameters update law 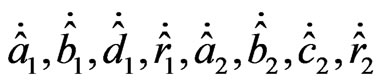 as follows:
as follows:
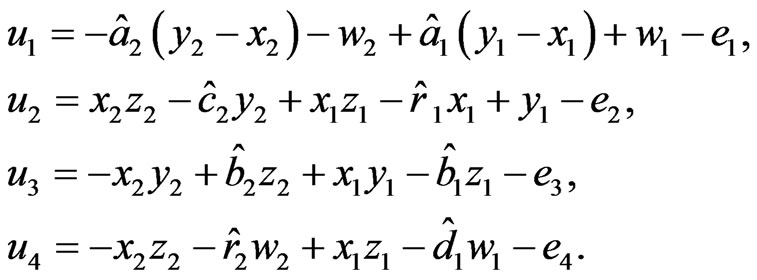 (25)
(25)
and the parameter update rule
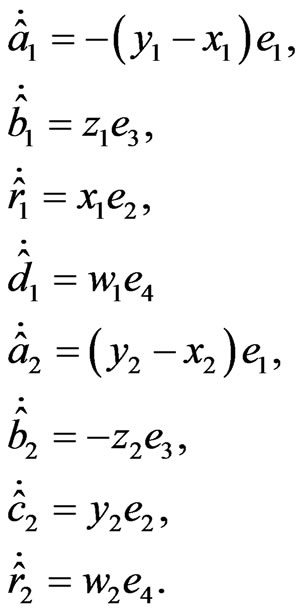 (26)
(26)
Consider the following Lyapunov function

Then the time derivative of 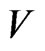 along the trajectories of Equation (24) is
along the trajectories of Equation (24) is
 (27)
(27)
Since 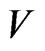 is positive definite function and
is positive definite function and  is negative definite function, it translates to
is negative definite function, it translates to 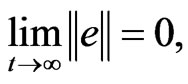 based on the Lyapunov stability theorem [31]. Therefore, the hyperchaotic Lű response system (14) is hybrid synchronized the hyperchaotic Lorenz drive system (15) with fully uncertain parameters under the adaptive controller (25) and the parameters update law (26).
based on the Lyapunov stability theorem [31]. Therefore, the hyperchaotic Lű response system (14) is hybrid synchronized the hyperchaotic Lorenz drive system (15) with fully uncertain parameters under the adaptive controller (25) and the parameters update law (26).
Numerical Simulations
To verify and demonstrate the effectiveness of the proposed method, we discuss the simulation result for the hybrid synchronization between hyperchaotic Lorenz

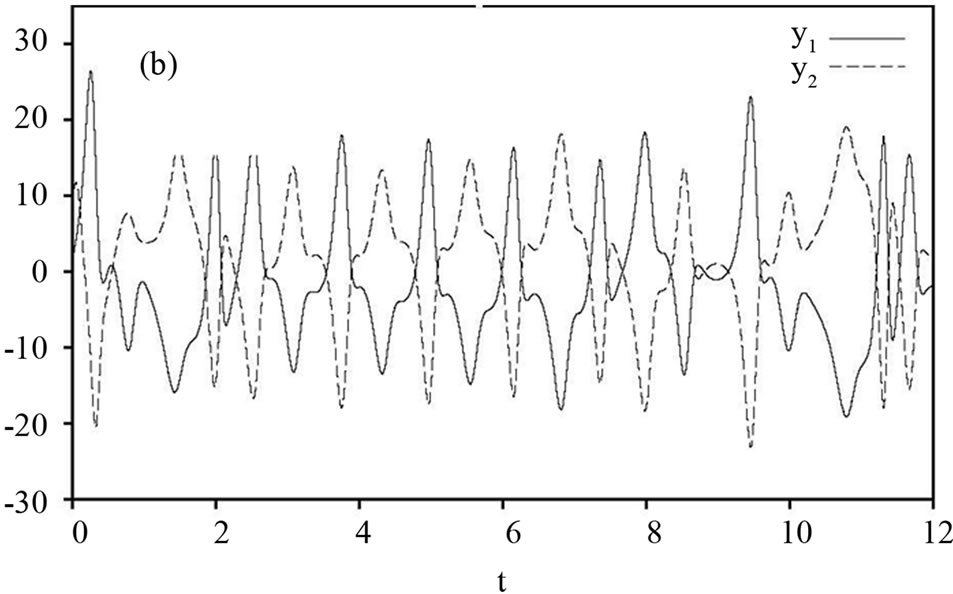
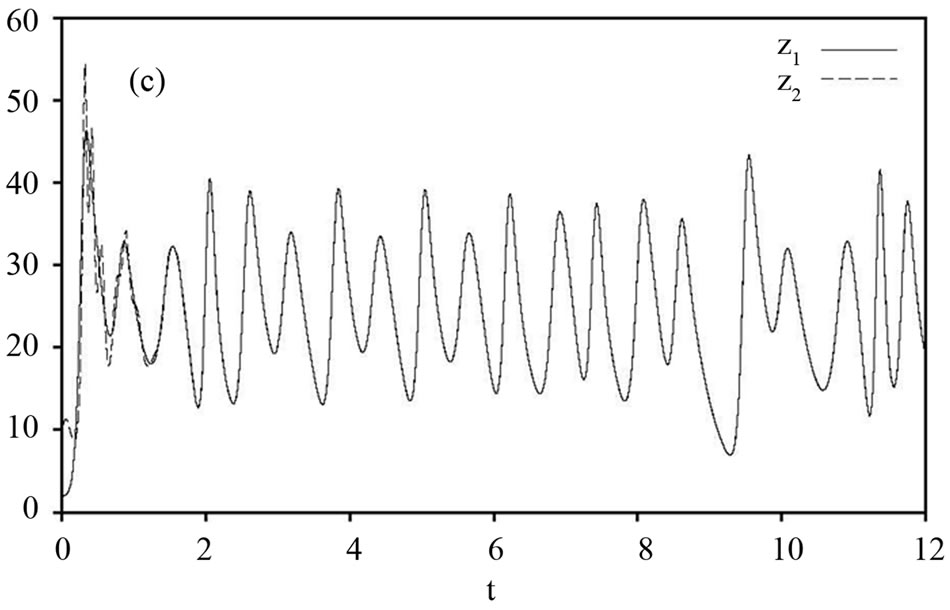
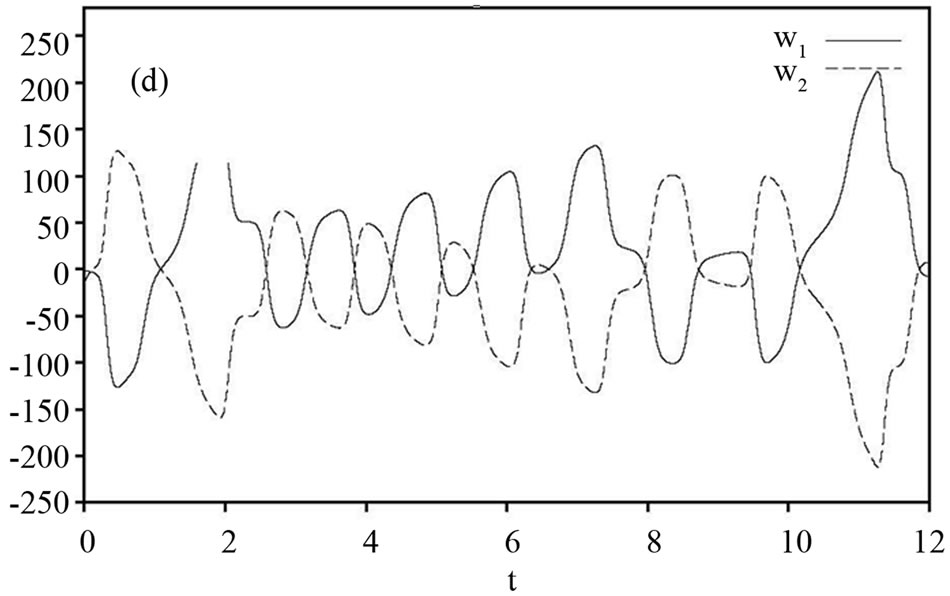
Figure 3. State trajectories of the drive system (22) and the response system (23). (a) Signals  and
and ; (b) Signals
; (b) Signals 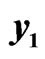 and
and ; (c) Signals
; (c) Signals 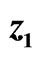 and
and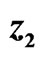 ; and (d) Signals
; and (d) Signals 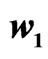 and
and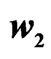 .
.
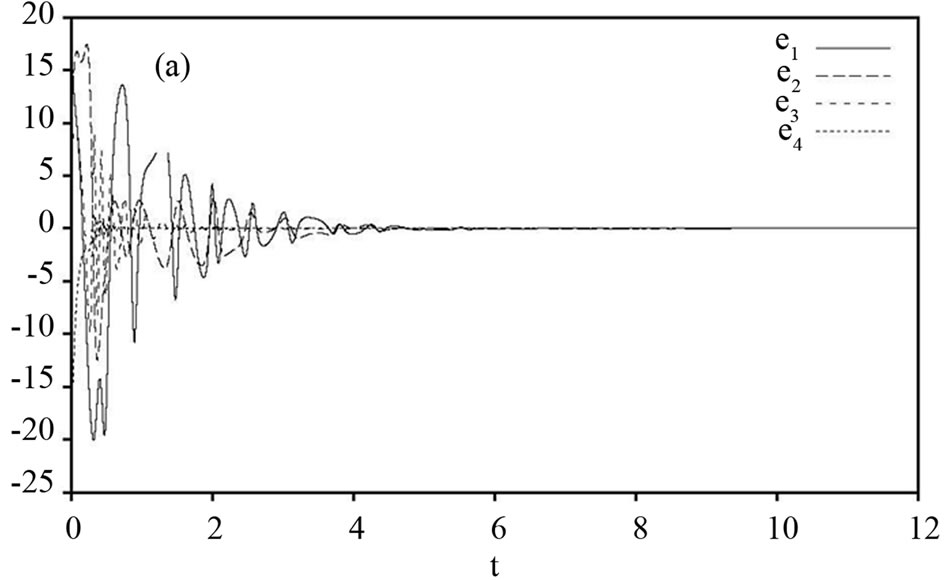
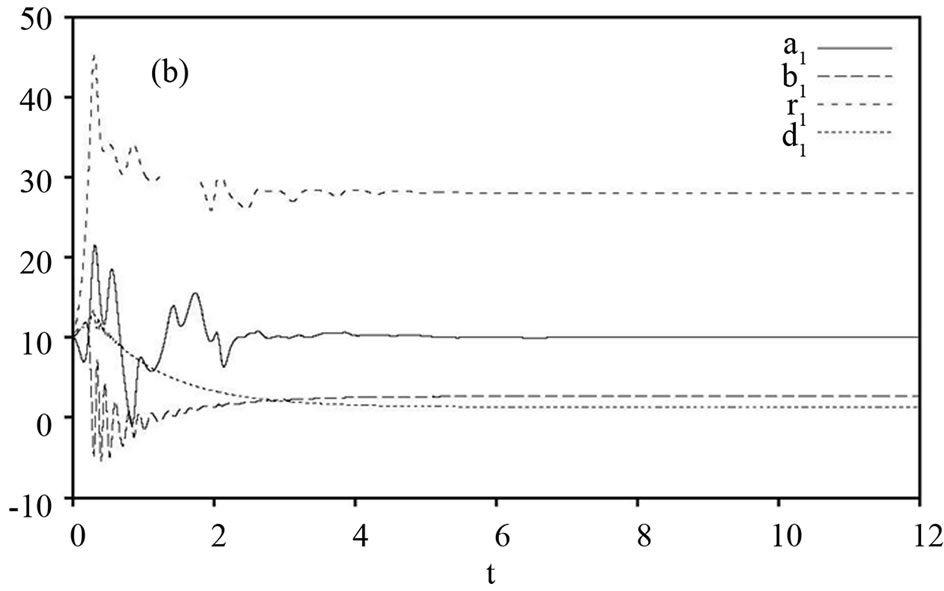
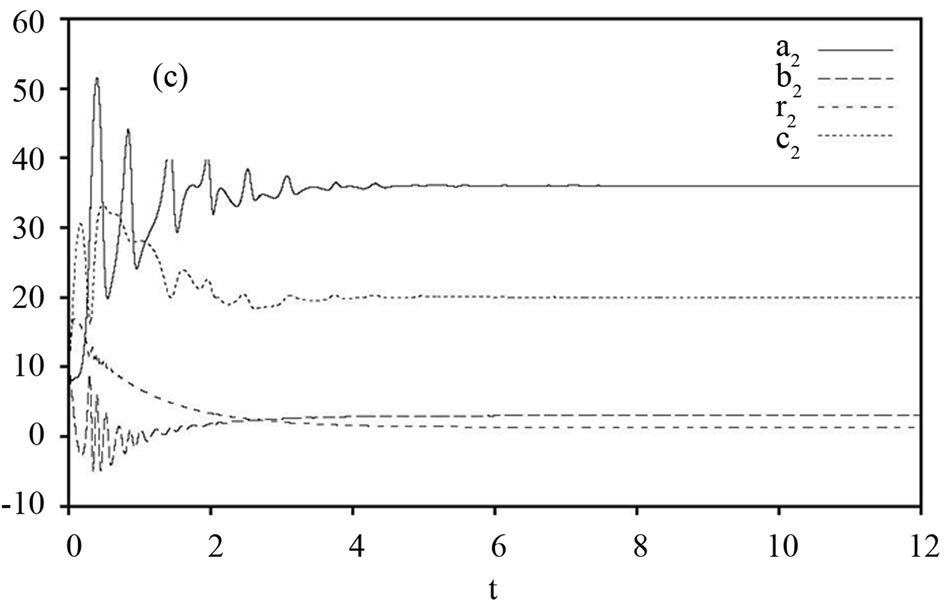
Figure 4. (a) Hybrid synchronization errors, 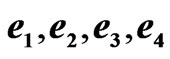 of the drive system (22) and the response system (23) with time
of the drive system (22) and the response system (23) with time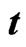 ; (b) and (c) Changing parameters
; (b) and (c) Changing parameters  of the drive system (22) and the response system (23) with time
of the drive system (22) and the response system (23) with time .
.
system and hyperchaotic Lű system. In the numerical simulations, the fourth-order Runge-Kutta method is used to solve the systems with time step size 0.001. For this numerical simulation, we assume that the initial condition, 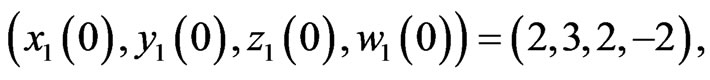 and
and 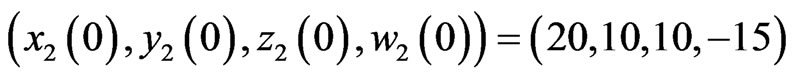 is employed. Hence the error system has the initial values
is employed. Hence the error system has the initial values  and
and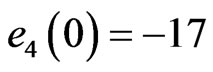 . The unknown parameters are chosen as
. The unknown parameters are chosen as
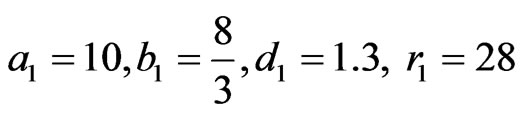 and
and
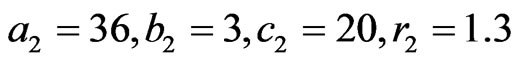 in simulations so that both the systems exhibits a hyperchaotic behavior. Hybrid synchronization of and (26) with the initial estimated parameters
in simulations so that both the systems exhibits a hyperchaotic behavior. Hybrid synchronization of and (26) with the initial estimated parameters
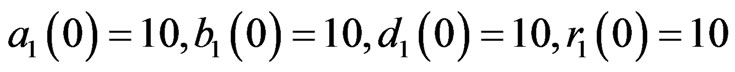 and
and 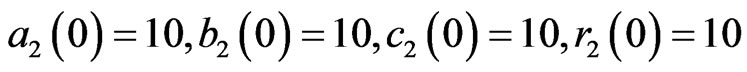 are shown in Figures 3 and 4. Figure 3 displays state trajectories of drive system (22) and the response system (23). Figure 4(a) displays the hybrid synchronization errors between system (22) and (23). Figures 3(b) and (c) show that the estimates
are shown in Figures 3 and 4. Figure 3 displays state trajectories of drive system (22) and the response system (23). Figure 4(a) displays the hybrid synchronization errors between system (22) and (23). Figures 3(b) and (c) show that the estimates  and
and 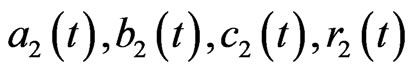 of the unknown parameters converges to
of the unknown parameters converges to 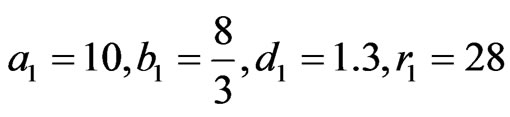 and
and
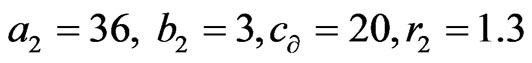 as
as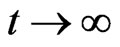 .
.
5. Conclusion
In this paper, we discussed the problem of adaptive hybrid synchronization of hyperchaotic systems with fully unknown parameters. On the basis of the Lyapunov stability theory and the adaptive control theory, a new adaptive hybrid synchronization control law and a novel parameter estimation update law are proposed to achieve hybrid synchronization between the two identical and different hyperchaotic systems with uncertain parameters. This shows that our proposed method has strong robustness. Finally, the simulation results are presented to show the effectiveness of this approach.
REFERENCES
- A. C. J. Luo, “A Theory for Synchronization of Dynamical Systems,” Communications in Nonlinear Science and Numerical Simulation, Vol. 4, No. 5, 2009, pp. 1901- 1951. http://dx.doi.org/10.1016/j.cnsns.2008.07.002
- F. Dou, J. Sun, W. Duan and K. Lu, “Controlling Hyperchaos in the New Hyperchaotic System,” Communications in Nonlinear Science and Numerical Simulation, Vol. 14, No. 2, 2009, pp. 552-559. http://dx.doi.org/10.1016/j.cnsns.2007.10.009
- M. Rafikov and J. Balthazar, “On Control and Synchronization in Chaotic and Hyperchaotic Systems via Linear Feedback Control,” Communications in Nonlinear Science and Numerical Simulation, Vol. 13, No. 7, 2008, pp. 1246-1255. http://dx.doi.org/10.1016/j.cnsns.2006.12.011
- M. C. Ho, Y. C. Hung and C. H. Chou, “Phase and AntiPhase Synchronization of two Chaotic Systems by Using Active Control,” Physics Letters A, Vol. 296, No. 1, 2002, pp. 43-48. http://dx.doi.org/10.1016/S0375-9601(02)00074-9
- G. H Li and S. P. Zhou, “Anti-Synchronization in Different Chaotic Systems,” Chaos, Solitons & Fractals, Vol. 32, No. 2, 2007, pp. 516-520. http://dx.doi.org/10.1016/j.chaos.2006.05.076
- Z. Wang, “Anti-Synchronization in Two Non-Identical Hyperchaotic Systems with Known or Unknown Parameters,” Communications in Nonlinear Science and Numerical Simulation, Vol. 14, No. 5, 2008, pp. 2366-2372. http://dx.doi.org/10.1016/j.cnsns.2008.06.027
- M. M. Al-Sawalha and M. S. M. Noorani, “Adaptive Anti-Synchronization of Chaotic Systems with Fully Unknown Parameters,” Computers & Mathematics with Applications, Vol. 59, No. 10, 2010, pp. 3234-3244. http://dx.doi.org/10.1016/j.camwa.2010.03.010
- M. M. Al-Sawalha and M. S. M. Noorani, “Adaptive Anti-Synchronization of two Identical and Different Hyperchaotic Systems with Uncertain Parameters,” Communications in Nonlinear Science and Numerical Simulation, Vol. 15, No. 4, 2010, pp. 1036-1047. http://dx.doi.org/10.1016/j.cnsns.2009.05.037
- M. M. Al-Sawalha and M. S. M. Noorani, “On AntiSynchronization of Chaotic Systems via Nonlinear Controll,” Chaos, Solitons & Fractals, Vol. 42, No. 1, 2009, pp. 170-179. http://dx.doi.org/10.1016/j.chaos.2008.11.011
- M. M. Al-Sawalha and M. S. M. Noorani, “Anti-Synchronization of two Hyperchaotic Systems via Nonlinear Control,” Communications in Nonlinear Science and Numerical Simulation, Vol. 14, No. 8, 2009, pp. 3402-3411. http://dx.doi.org/10.1016/j.cnsns.2008.12.021
- L. Ruihong, X. Wei and L, Shuang, “Anti-Synchronization on Autonomous and Non-Autonomous Chaotic Systems via Adaptive Feedback Control,” Chaos, Solitons & Fractals, Vol. 40, 2007, pp. 1288-1296.
- J. Feng, S. Chen and C. Wang, “Adaptive Synchronization of Uncertain Hyperchaotic Systems Based on Parameter Identification,” Chaos, Solitons & Fractals, Vol. 26, No. 4, 2005, pp. 1163-1169. http://dx.doi.org/10.1016/j.chaos.2005.02.027
- S. Chen, J. Hua, C. Wang and J. Lu, “Adaptive Synchronization of Uncertain Rossler Hyperchaotic System Based on Parameter Identification,” Physics Letters A, Vol. 321, No. 1, 2004, pp. 50-55. http://dx.doi.org/10.1016/j.physleta.2003.12.011
- X. Wu and H. Zhang, “Synchronization of Two Hyperchaotic Systems via Adaptive Control,” Chaos, Solitons & Fractals, Vol. 39, No. 5, 2009, pp. 2268-2273. http://dx.doi.org/10.1016/j.chaos.2007.06.100
- X. Wua, Z. Guana and Z. Wua, “Adaptive Synchronization between Two Different Hyperchaotic Systems,” Nonlinear Analysis, Vol. 68, No. 5, 2008, pp. 1346-1351. http://dx.doi.org/10.1016/j.na.2006.12.028
- T. Gao, Z. Chen, Z. Yuan and D. Yu, “Adaptive Synchronization of a New Hyperchaotic System with Uncertain Parameters,” Chaos, Solitons & Fractals, Vol. 33, No. 3, 2007, pp. 922-928. http://dx.doi.org/10.1016/j.chaos.2006.01.042
- B. Wang and G. Wen, “On the Synchronization of a Hyperchaotic System Based on Adaptive Method,” Physics Letters A, Vol. 372, No. , 2008, pp. 3015-3020. http://dx.doi.org/10.1016/j.physleta.2008.01.019
- Q. Jia, “Adaptive Control and Synchronization of a New Hyperchaotic System with Unknown Parameters,” Physics Letters A, Vol. 362, No. 17, 2007, pp. 424-429. http://dx.doi.org/10.1016/j.physleta.2006.10.044
- H. Zhang, W. Huang, Z. Wang and T. Chai, “Adaptive Synchronization between Two Different Chaotic Systems with Unknown Parameters,” Physics Letters A, Vol. 350, No. 5-6, 2006, pp. 363-366. http://dx.doi.org/10.1016/j.physleta.2005.10.033
- R. H. Li, “A Special Full-State Hybrid-Synchronization in Symmetrical Chaotic System,” Applied Mathematics and Computation, Vol. 200, No. 1, 2008, pp. 319-321. http://dx.doi.org/10.1016/j.amc.2007.11.010
- Q. Xie, G. Chen and E. M. Bollt, “Hybrid Chaos Synchronization and its Application in Information Processing,” Mathematical and Computer Modeling, Vol. 35, No. 1-2, 2002, pp. 145-163. http://dx.doi.org/10.1016/S0895-7177(01)00157-1
- Q. Zhang and J. Lu, “Full State Hybrid Lag Projective Synchronization in Chaotic (Hyperchaotic) Systems,” Physics Letters A, Vol. 372, No. 9, 2008, pp. 1416-1421. http://dx.doi.org/10.1016/j.physleta.2007.09.051
- J. Chen, H. Chen and Y. Lin, “Synchronization and AntiSynchronization Coexist in Chen-Lee Chaotic Systems,” Chaos Solitions & Fractals, Vol. 39, No. 2, 2009, pp. 707-716. http://dx.doi.org/10.1016/j.chaos.2007.01.104
- W. Sun, Z. Chen, Y. Lu and S. Chen, “An intriguing Hybrid Synchronization Phenomenon of Two Coupled Complex Networks,” Applied Mathematics and Computation, Vol. 216, No. 8, 2010, pp. 2301-2309. http://dx.doi.org/10.1016/j.amc.2010.03.066
- S. Vaidyanathan and S. Rasappan, “Hybrid Chaos Synchronization of 4D Hyperchaotic Qi and Jia Systems by Active Nonlinear Control,” International Journal of Distributed and Parallel Systems (IJDPS), Vol. 2, No. 2, 2011, pp. 83-94. http://dx.doi.org/10.5121/ijdps.2011.2208
- L. Yuxia, K. Wallace and G. Chen, “Generating Hyperchaos via State Feedback Control,” International Journal of Bifurcation and Chaos, Vol. 15, No. 10, 2005, pp. 3367-3375. http://dx.doi.org/10.1142/S0218127405013988
- J. Park, “Adaptive Synchronization of Hyperchaotic Chen System with Uncertain Parameters,” Chaos, Solitons & Fractals, Vol. 26, No. 3, 2005, pp. 959-964. http://dx.doi.org/10.1016/j.chaos.2005.02.002
- Q. Jia, “Hyperchaos Generated from the Lorenz Chaotic System and Its Control,” Physics Letters A, Vol. 366, No. 3, 2007, pp. 217-222. http://dx.doi.org/10.1016/j.physleta.2007.02.024
- Q. Jia, “Projective Synchronization of a New Hyperchaotic Lorenz System,” Physics Letters A, Vol. 370, No. 1, 2007, pp. 40-45. http://dx.doi.org/10.1016/j.physleta.2007.05.028
- A. Chen, J. Lu, J. Lu and S. Yu, “Generating Hyperchaotic Lu Attractor via State Feedback Control,” Physica A, Vol. 364, 2006, pp. 103-110. http://dx.doi.org/10.1016/j.physa.2005.09.039
- J. Lasalle and S. Lefschtg, “Stability by Lyapunovs Direct Method with Application,” Academic Press, New York, 1961.

