Applied Mathematics
Vol.4 No.11A(2013), Article ID:40118,7 pages DOI:10.4236/am.2013.411A1006
Stabilization of Functional System with Markovian Switching
School of Mathematics and Computer Science, Jianghan University, Wuhan, China
Email: fengliahu11@163.com
Copyright © 2013 Lizhu Feng, Qiong Cai. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received October 14, 2013; revised November 14, 2013; accepted November 21, 2013
Keywords: Stochastic Functional System; Brownian Noise; Markovian Switching; Boundedness; Stabilization
ABSTRACT
There are many papers related to stability, some on suppression or on stabilization are one type of them. Functional differential systems are common and important in practice. They are special situations of neutral differential systems and generalization of ordinary differential systems. We discussed conditions on suppression on functional system with Markovian switching in our previous work: “Suppression of Functional System with Markovian Switching”. Based on it, by slightly modifying and adding some conditions, we get this paper. In this paper, we will study a functional system whose coefficient satisfies the local Lipschitz condition and the one-sided polynomial growth condition under Markovian switching. By introducing two appropriate intensity Brownian noise, we find the potential explosion system stabilized.
1. Introduction
There are many papers which discuss stability of systems. It is called a stabilization problem when we impose such conditions on a given unstable system to make it stable. There have been rich literatures on this topic, here we only mention [1-4]. It is talked about suppression of noise in [1,2]. It is showed similar stabilization phenomena in stochastic systems as those in deterministic systems in [3,4]. They all indicate clearly that different structures of environmental noise may have different effects on the deterministic system. On the other hand, there are also many papers related to stabilization of functional systems, such as [5-8]. [5] investigates a stochastic Lotka-Volterra system with infinite delay, whose initial data come from an admissible Banach space C, and show that its unique global positive solution has asymptotic boundedness property by using the exponential martingale inequality. [6] studies existence and uniqueness of the global positive solution of stochastic functional Kolmogorov-type system and its asymptotic bound properties and moment average boundedness in time under the traditionally diagonally dominant condition. [7] studies the same problems as [6] under some other conditions. [8] discusses stabilization of a given unstable nonlinear functional system by introducing two Brownian noise.
Many practical systems may experience abrupt changes in their structure and parameters caused by phenomena such as component failures or repairs, changing subsystem interconnections, and abrupt environmental disturbances. The hybrid systems have been used to desribe such situations. Along the trajectories of the Markovian jump system, the mode switches from one value to another in a random way are governed by a Markov process with discrete state space. [9,10] studied the stability of a jump system. Feng et al. [11] systematically studied stochastic stability properties of jump linear systems and the relationship among various moment and sample path stability properties. Shen and Wang [12] presented new exponential stability results for recurrent neural networks with Markovian switching. Wang et al. [13] dealt with the problem of state estimation for a class of delayed neural networks with Markovian jumping parameters without the traditional monotonicity and smoothness assumptions on the activation function.
Taking both the environmental noise and jump into account, the system under consideration becomes a stochastic differential system with Markovian switching (SDSwMS), which has received a lot of attention (see [14-24]) recently. [17] provided some useful conditions on the exponential stability for general nonlinear SDSwMSs, which was improved by himself in Mao et al. [19]. Yuan and Lygeros [20] investigated almost sure exponential stability for a class of switching diffusion processes. [25] discusses the asymptotic stability and exponential stability of SDSwMSs, whose coefficients are assumed to satisfy the local Lipschitz condition and the polynomial growth condition.
Motivated by [25,26] and some other literatures, we will investigate suppression and stabilization by noise of functional differential system with Markov chains, whose coefficient satisfies the local Lipschitz condition and the one-sided polynomial growth condition. For a given unstable functional system with Markovian switching
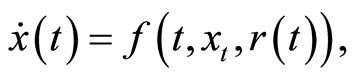 (1)
(1)
where
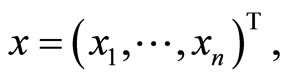

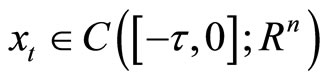 is defined by
is defined by , by introducing two independent scalar Brownian noise under some conditions, we get a stochastic functional system which admits a unique global positive solution. Furthermore, choosing appropriate intensity noise, we can get an exponential stable stochastic functional system
, by introducing two independent scalar Brownian noise under some conditions, we get a stochastic functional system which admits a unique global positive solution. Furthermore, choosing appropriate intensity noise, we can get an exponential stable stochastic functional system
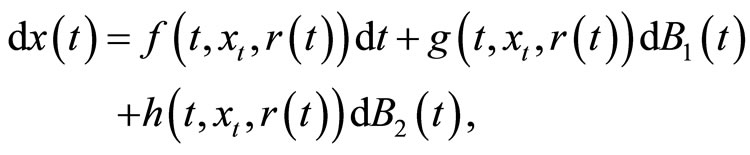 (2)
(2)
on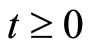 , where
, where 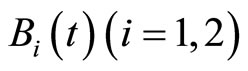 is a scalar Brownian motion, and
is a scalar Brownian motion, and
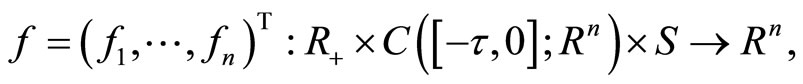
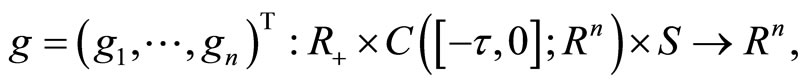
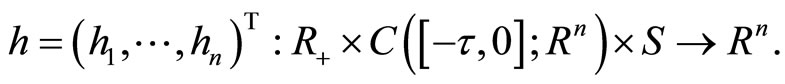
In the next section we will give some necessary notations and lemmas. In Section 3, we will give the main results of this paper.
2. Preliminaries
Throughout this paper, unless otherwise specified, let  be the Euclidean norm in
be the Euclidean norm in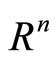 . If
. If 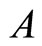 is a vector or matrix, its transpose is denoted by
is a vector or matrix, its transpose is denoted by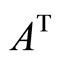 . If
. If 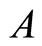 is a matrixits trace norm is denoted by
is a matrixits trace norm is denoted by . Denote the inner product of
. Denote the inner product of 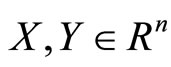 by
by 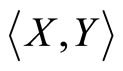 or
or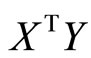 . Let
. Let 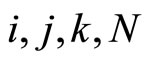 be positive integers. Let
be positive integers. Let 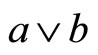 denote the maximum of
denote the maximum of 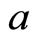 and
and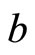 , while
, while 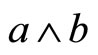 the minimum of
the minimum of 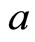 and
and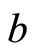 . Let
. Let 
 . Denote by
. Denote by 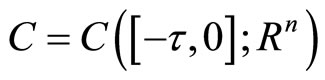 the family of continuous functions from
the family of continuous functions from 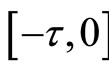 to Rn with the norm
to Rn with the norm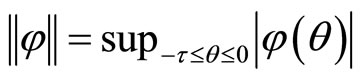 which forms a Banach space. Let
which forms a Banach space. Let 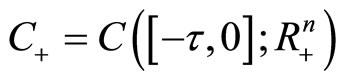 and
and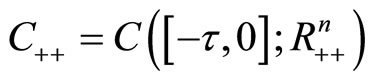 . Let
. Let  denote the family of functions
denote the family of functions  on
on  which are continuously twice differentiable in
which are continuously twice differentiable in  and once in
and once in .
.
Let 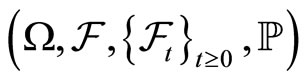 be a complete probability space with a filtration
be a complete probability space with a filtration 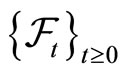 satisfying the usual conditions (i.e. it is increasing and right continuous while
satisfying the usual conditions (i.e. it is increasing and right continuous while 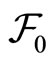 contains all
contains all 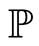 -null sets). Let
-null sets). Let 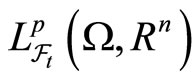 denote the family of
denote the family of 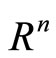 -valued
-valued  -measurable random variables
-measurable random variables 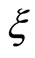 with
with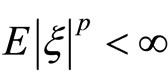 . Denote the family of Rn-valued bounded
. Denote the family of Rn-valued bounded 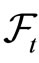 -measurable random variables by
-measurable random variables by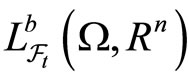 . If
. If 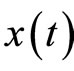 is an Rn-valued process on
is an Rn-valued process on , let
, let
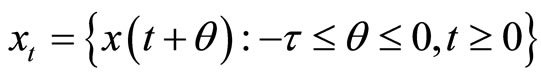 .
.
If 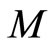 is a continuous local martingale, denote the quadratic variation of
is a continuous local martingale, denote the quadratic variation of 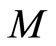 by
by . Let
. Let
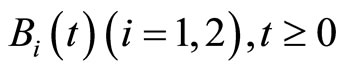
be independent scalar Brownian motion defined on the probability space. Let 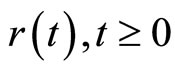 be a right-continuous Markov chain on the probability space taking values in a definite state space
be a right-continuous Markov chain on the probability space taking values in a definite state space 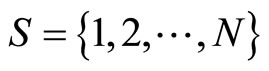 with the generator
with the generator 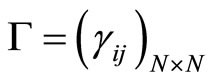 given by
given by
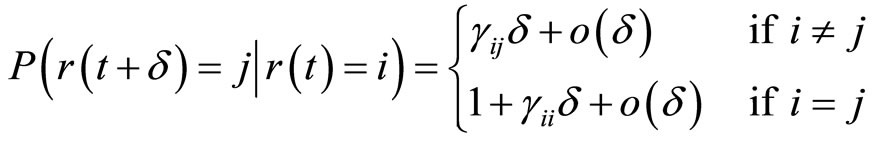
where 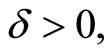
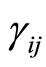 is the transition rate from
is the transition rate from 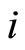 to
to 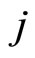 and
and 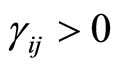 if
if 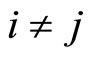 while
while . We assume that the Markov chain
. We assume that the Markov chain 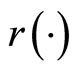 is independent of the Brownian motion
is independent of the Brownian motion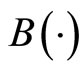 . For any initial value
. For any initial value 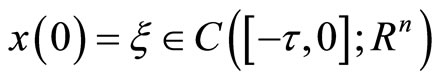 denote the solution of the corresponding initial value problem by
denote the solution of the corresponding initial value problem by 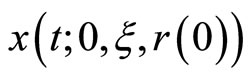 or simply
or simply 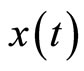 on
on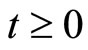 .
.
In order to obtain the main results, we need the following assumptions.
(H1) There are some nonnegative constants 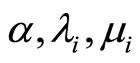 such that
such that
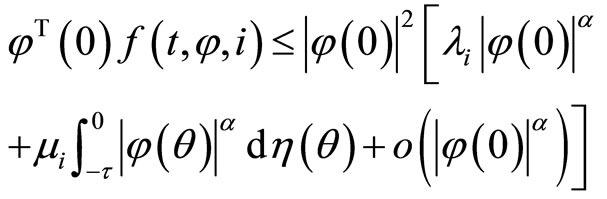 (3)
(3)
for all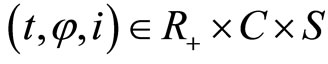 , where
, where 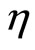 is a probability measure on
is a probability measure on 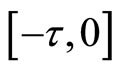 and
and  means some functions satisfying
means some functions satisfying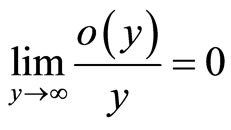 .
.
(H2) For every integer , there is a
, there is a  such that
such that
 (4)
(4)
for all 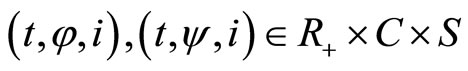 with
with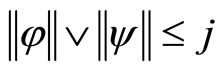 .
.
(H3) There are some nonnegative constants 
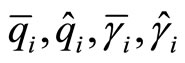 and probability measure
and probability measure 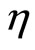 such that for any
such that for any 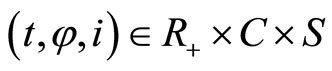 satisfying
satisfying ,
,
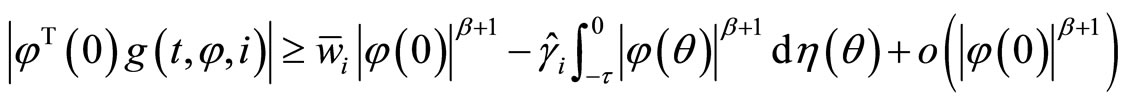 (5)
(5)
 (6)
(6)
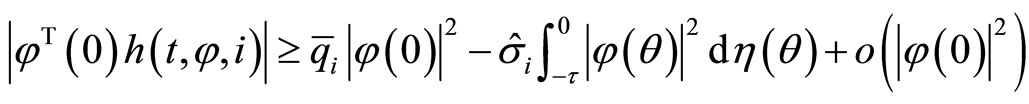 (7)
(7)
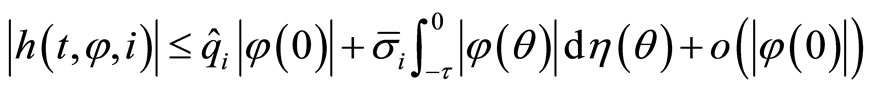 . (8)
. (8)
Definition 1: The irreducibility of the Markov chain means that the Markov chain has a unique stationary (probability) distribution  which can be determined by solving the following linear equation
which can be determined by solving the following linear equation
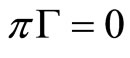 (9)
(9)
subject to
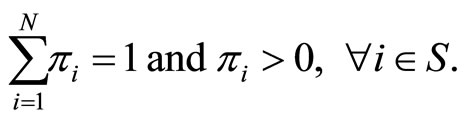 (10)
(10)
Lemma 1: [27] Let (H2) hold, for any initial value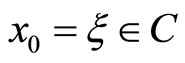 , system (2) has a unique maximal local strong solution on
, system (2) has a unique maximal local strong solution on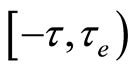 , where
, where 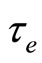 is the explosion time.
is the explosion time.
3. Main Results
Similar to the proof of Theorem 1 in [28], we slightly modify the condition on the coefficient of (1) and obtain the following theorem.
Theorem 1: Let (H1) - (H3) hold, for any initial value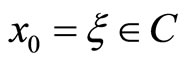 , if
, if 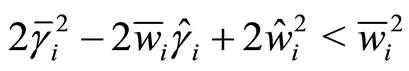 and
and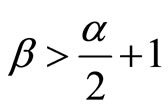 then there exists a unique global solution
then there exists a unique global solution 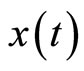 of system (2) on all
of system (2) on all  a.s.
a.s.
Similarly to that in [28], we define the stopping time
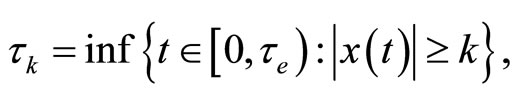 (11)
(11)
and a C2-function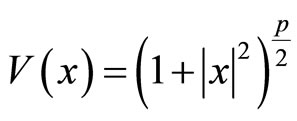 , for any
, for any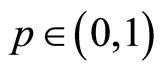 .
.
Using the Itô formula and the Young inequality, for any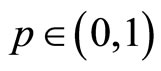 , by (H1) and (H3), we get
, by (H1) and (H3), we get
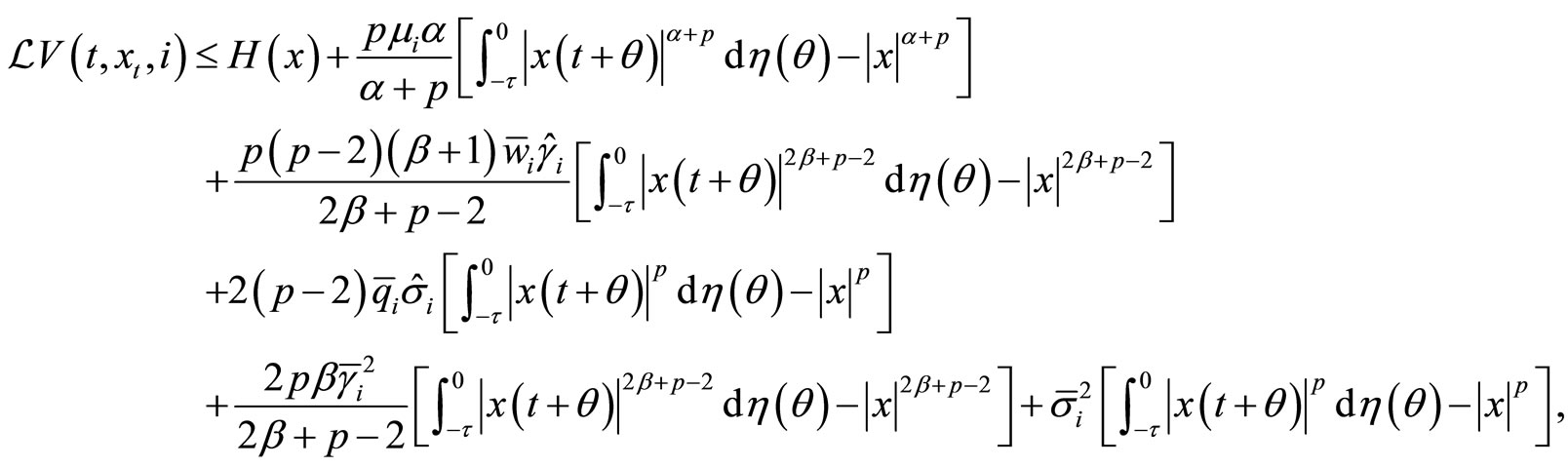 (12)
(12)
where
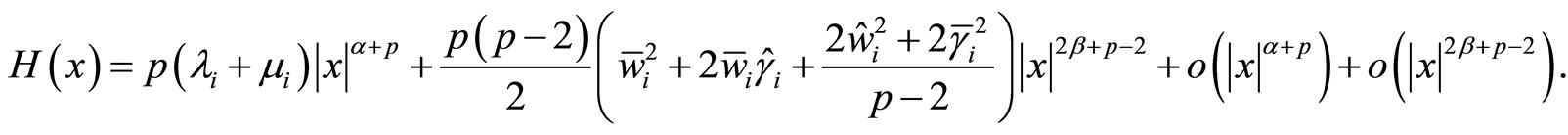 (13)
(13)
These results will be used in the following.
3.1. Boundedness
Theorem 2: Let (H1) - (H3) hold, for any initial value 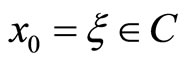 and
and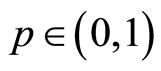 , if
, if 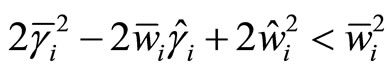 and
and , then there exists a constant
, then there exists a constant 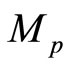 such that the global solution
such that the global solution  of system (2) has the property that
of system (2) has the property that
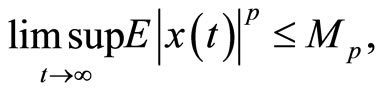 (14)
(14)
where 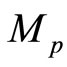 is dependent on
is dependent on 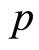 and independent of the initial value
and independent of the initial value , that is,
, that is, 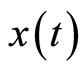 is bounded in moment.
is bounded in moment.
Proof: For any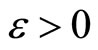 , applying the Itô formula to
, applying the Itô formula to 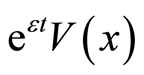 yields
yields

By (12) and (13), we have
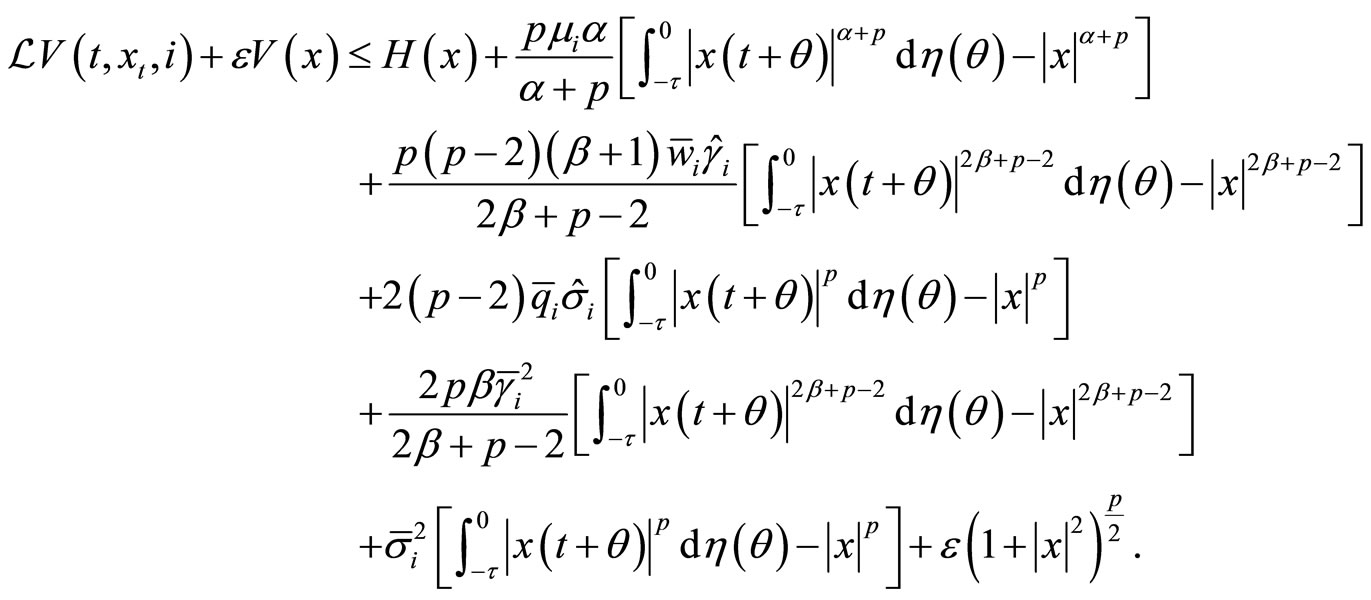
By the boundedness of polynomial functions, there exists a constant 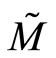 such that
such that 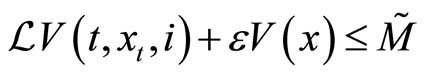 which implies
which implies
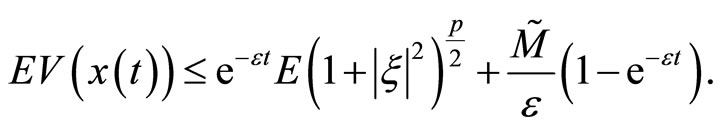
Then
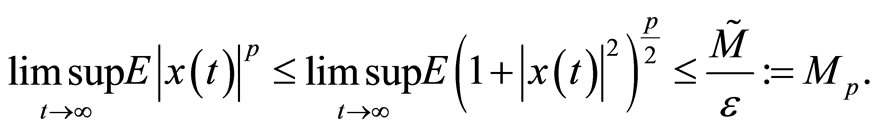
That is, the global solution 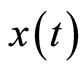 of system (2) is bounded in
of system (2) is bounded in 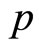 -th moment for any
-th moment for any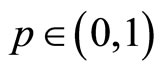 .
.
Theorem 3: Let (H1) - (H3) hold, if
 and
and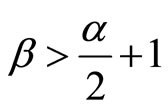
then for any initial value 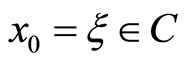 and
and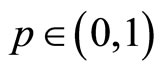 , the solution
, the solution 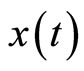 of system (2) has the property that
of system (2) has the property that
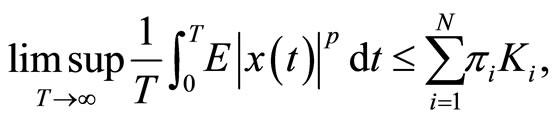 (15)
(15)
where
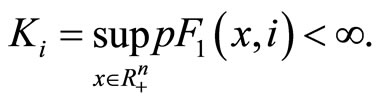
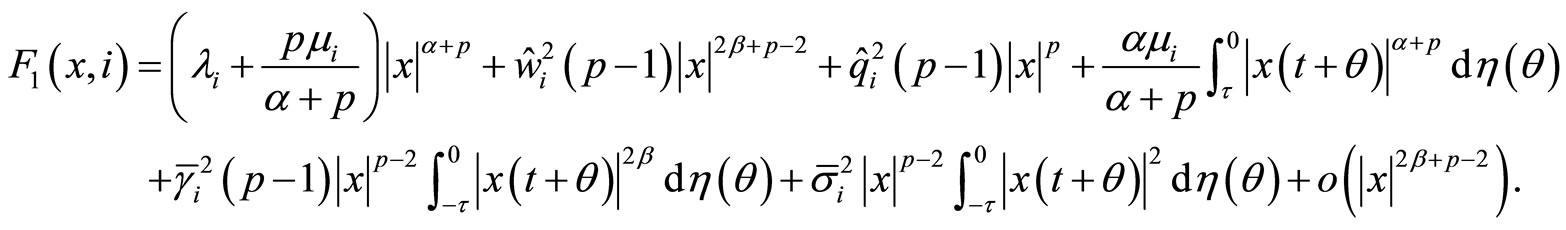 (16)
(16)
Proof: By Theorem 1, there a.s. exists a unique global solution  to system (2) on
to system (2) on  a.s. Let
a.s. Let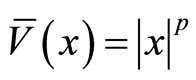 , by the Itô formula, we have
, by the Itô formula, we have

where
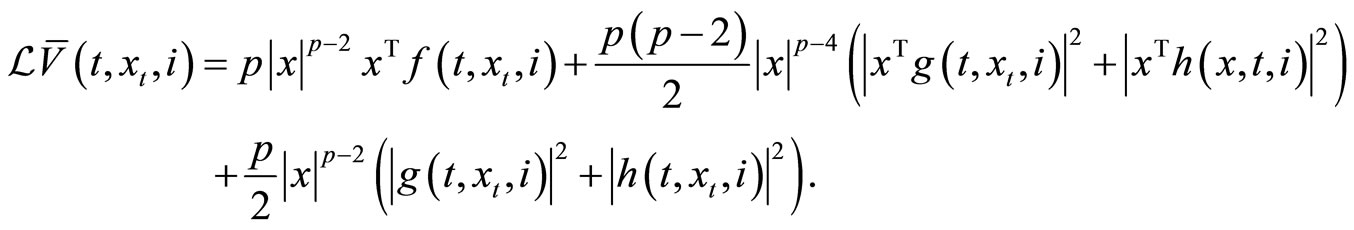
By (H1) and (H3), we have
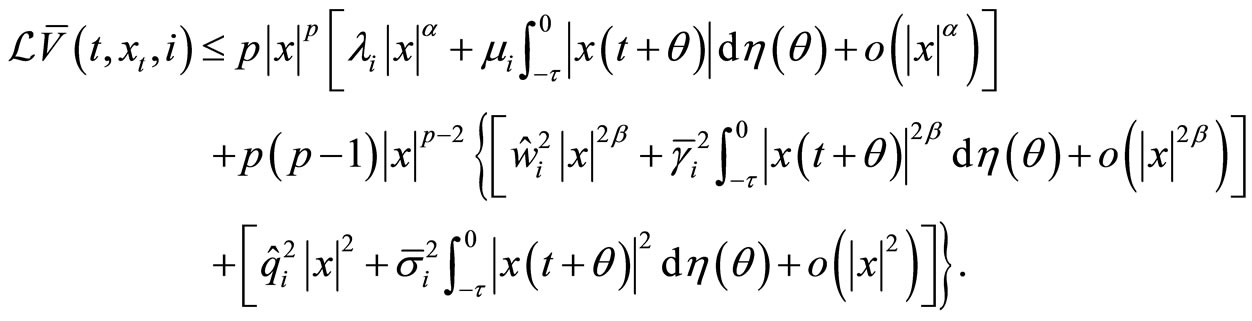
Let 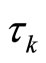 be the same stopping time as defined in the proof of Theorem 1. By (13) and (14), we have
be the same stopping time as defined in the proof of Theorem 1. By (13) and (14), we have
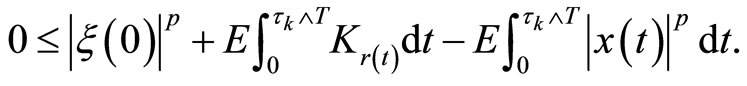
Then as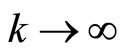 , we have
, we have
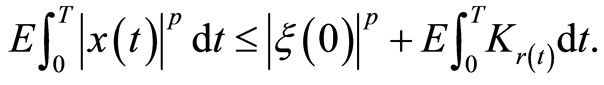
That is,
 (17)
(17)
By the ergodic and irreducibility property of the Markov chain, we have
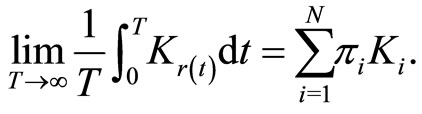
Hence,
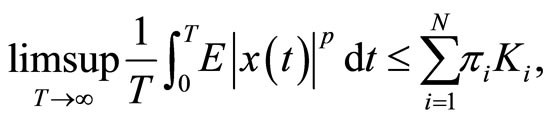
as required.
3.2. Stabilization of Noise
The following lemma can be obtained by slightly modifying the proof of Mao [2].
Lemma 2: Let (H1) - (H3) hold, for any initial value 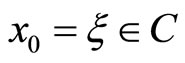 with
with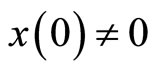 , the global solution of system (2) has the property that
, the global solution of system (2) has the property that
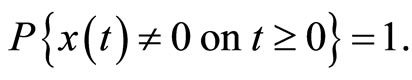 (18)
(18)
where 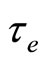 is the explosion time.
is the explosion time.
Theorem 4: Let (H1) - (H3) hold, assume that
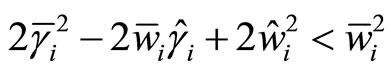 and
and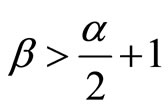 .
.
If
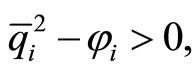 (19)
(19)
where
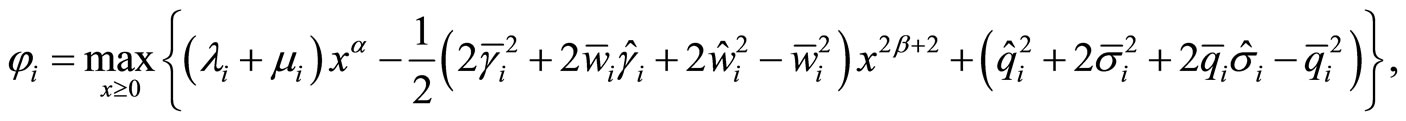 (20)
(20)
then for any initial value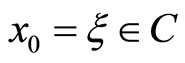 , satisfying
, satisfying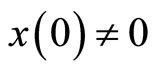 , the global solution of system (2) has the property that
, the global solution of system (2) has the property that
 (21)
(21)
That is, the solution to system (2) is a.s. exponentially stable.
Proof: By Lemma 2 and Theorem 1, 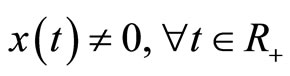 a.s. Thus, applying the Itô formula to
a.s. Thus, applying the Itô formula to 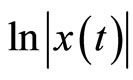 yields
yields
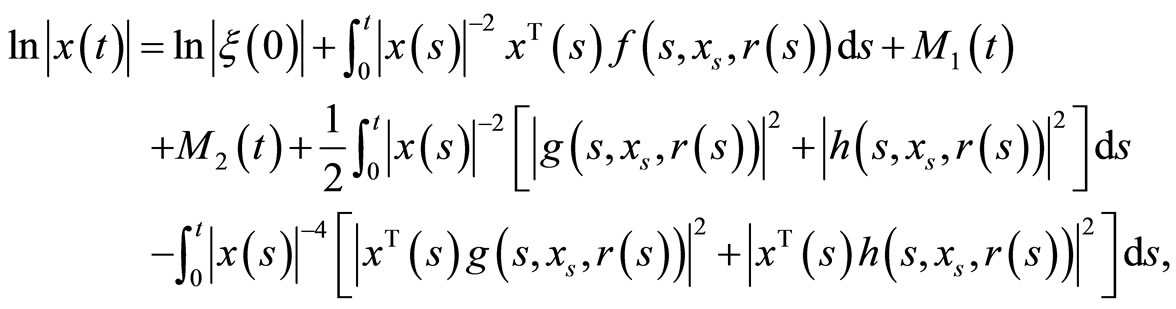
where 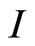 is an identity matrix and
is an identity matrix and
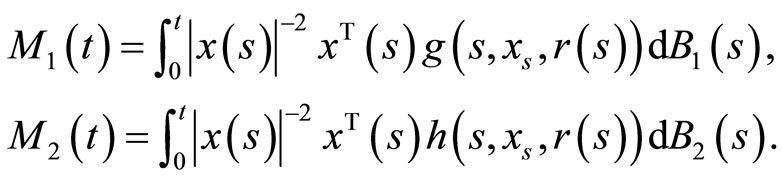
Clearly  and
and 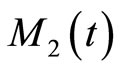 are continuous local martingales with the quadratic variation
are continuous local martingales with the quadratic variation
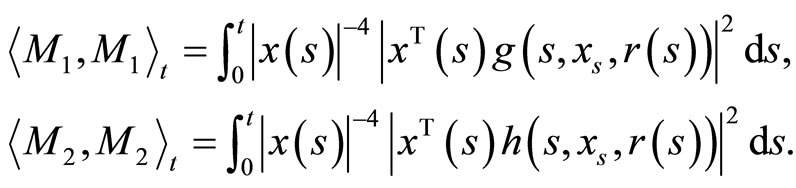
By (H3),
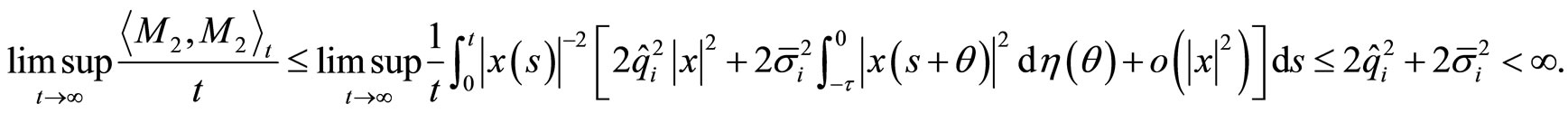
Applying the strong law of large number,
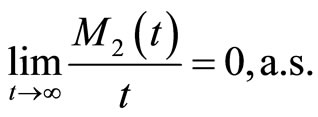
For any  and each integer
and each integer , by the exponential martingale inequality,
, by the exponential martingale inequality,
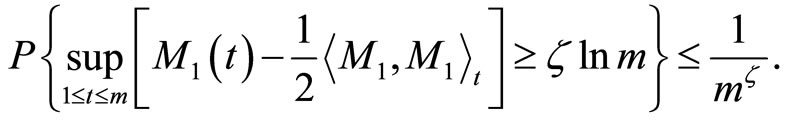
Since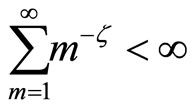 , by the Borel-Cantelli lemma, there exists an
, by the Borel-Cantelli lemma, there exists an 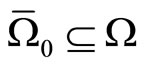 with
with 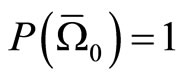 such that for any
such that for any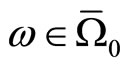 , when
, when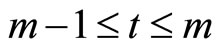 ,
,
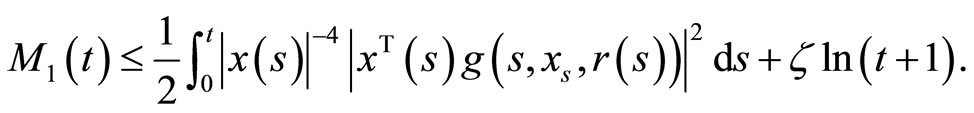
From (H1) and (H3),
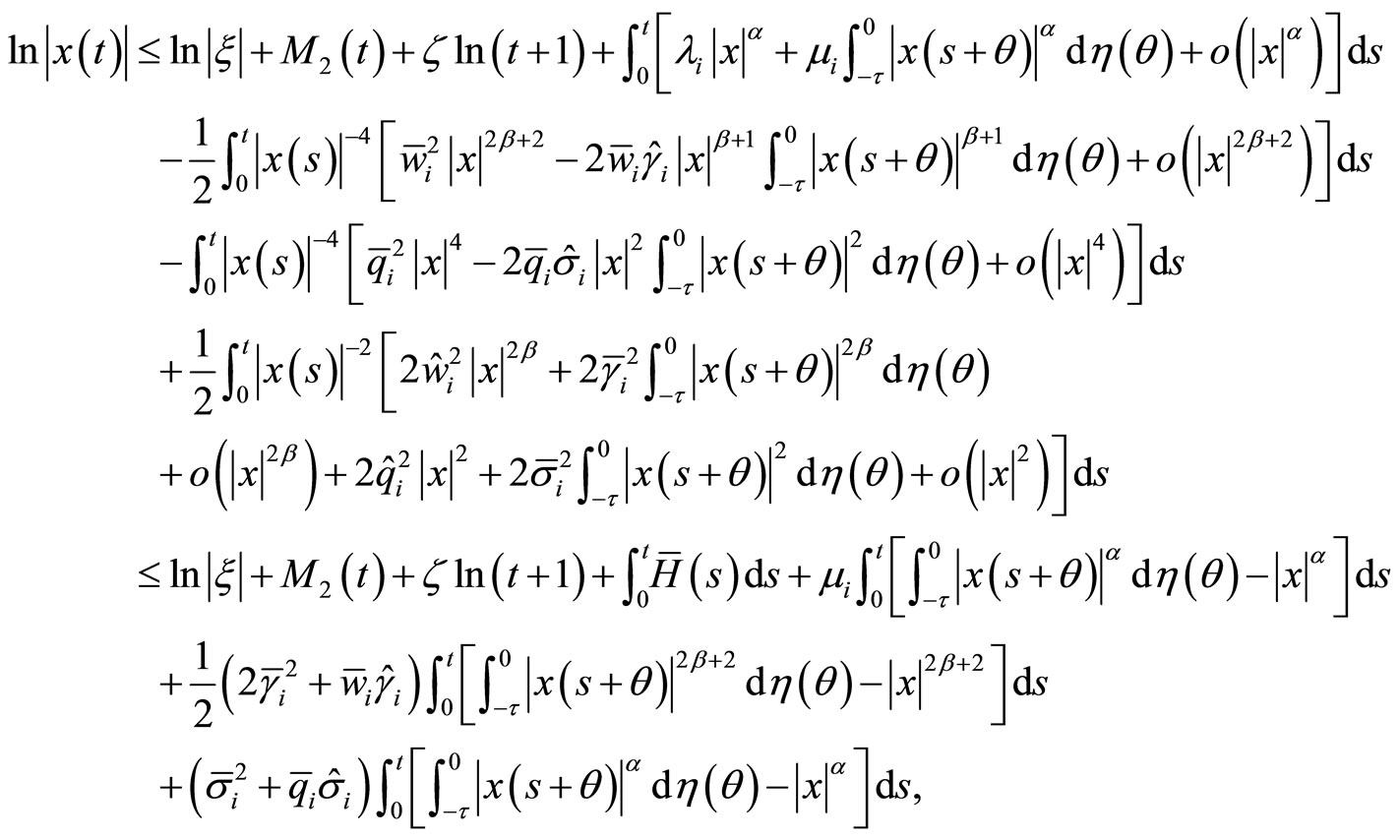
where
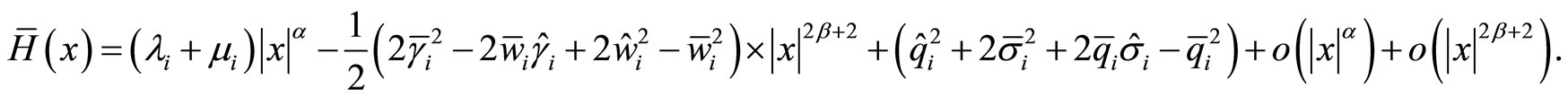
By the definition of  in (20),
in (20),
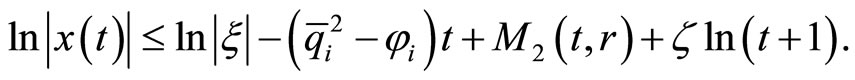
Applying the strong law of large number to the Brownian motion,

which implies
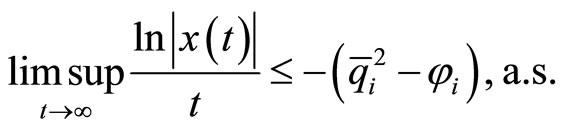
4. Conclusion
In this paper, we study a stochastic functional system with Markovian switching. Motivated by [25,26] and other literatures, we introduce two appropriate intensity Brownian noise to perturb the system so as to suppress its potential explosion and stabilize it. Based on [28], we just slightly modify some conditions on its coefficients and add some contents, then we get some new conclusions about boundedness and stabilization of the system.
REFERENCES
- X. Mao, G. Marion and E. Renshaw, “Environmental Noise Suppresses Explosion in Population Dynamics,” Stochastic Processes and their Applications, Vol. 97, No. 1, 2002, pp. 96-110. http://dx.doi.org/10.1016/S0304-4149(01)00126-0
- J. K. Hale and J. Kato, “Phase Space for Retarded Equations with Infinite Delay,” Funkcial Ekvac, Vol. 21, 1978, pp. 11-41.
- X. Mao, S. Sabanis and E. Renshaw, “Asymptotic Behaviour of the Stochastic Lotka-Volterra Model,” Journal of Mathematical Analysis and Applications, Vol. 287, No. 1, 2003, pp. 141-156. http://dx.doi.org/10.1016/S0022-247X(03)00539-0
- Y. Song and C. T. H. Baker, “Qualitative Behaviour of Numerical Approximations to Volterra Integro-Differential Equations,” Journal of Computational and Applied Mathematics, Vol. 172, No. 1, 2004, pp. 101-115. http://dx.doi.org/10.1016/j.cam.2003.12.049
- F. Wu and S. Hu, “Positive Solution and Its Asymptotic Behaviour of Stochastic Functional Kolmogorov-Types System,” Journal of Mathematical Analysis and Applications, Vol. 364, No. 1, 2012, pp. 104-118. http://dx.doi.org/10.1016/j.jmaa.2009.10.072
- Y. Xu, F. Wu and Y. Tan, “Stochastic Lotka-Volterra System with Infinite Delay,” Journal of Computational and Applied Mathematics, Vol. 232, No. 2, 2009, pp. 472-480. http://dx.doi.org/10.1016/j.cam.2009.06.023
- F. Wu, X. Mao and S. Hu, “Stochastic Suppression and Stabilization of Functional Differential Equations,” Systems & Control Letters, Vol. 59, No. 12, 2010, pp. 745- 753. http://dx.doi.org/10.1016/j.sysconle.2010.08.011
- F. Wu and S. Hu, “Stochastic Functional KolmogorovType Population Dynamics,” Journal of Mathematical Analysis and Applications, Vol. 347, No. 2, 2008, pp. 534-548. http://dx.doi.org/10.1016/j.jmaa.2008.06.038
- Y. Ji and H. J. Chizeck, “Controllability, Stabilizability and Continuous-Time Markovian Jump Linear Quadratic Control,” IEEE Transaction on Automatic Control, Vol. 35, No. 7, 1990, pp. 777-788. http://dx.doi.org/10.1109/9.57016
- M. Marition, “Jump Linear Systems in Automatic Control,” Marcel Dekker, New York, 1990.
- X. Feng, K. A. Loparo, Y. Ji and H. J. Chizeck, “Stochastic Stability Properties of Jump Linear Systems,” IEEE Trans. Automat. Control, Vol. 31, 1992, pp. 38-53. http://dx.doi.org/10.1109/9.109637
- Y. Shen and J. Wang, “Almost Sure Exponential Stability of Recurrent Neural Networks with Markovian Switching,” IEEE Transaction on Neural Network, Vol. 20, No. 5, 2009, pp. 840-855. http://dx.doi.org/10.1109/TNN.2009.2015085
- Z. Wang, Y. Liu and X. Liu, “State Estimation for Jumping Recurrent Neural Networks with Discrete and Distributed Delays,” Neural Networks, Vol. 22, No. 1, 2009, pp. 41-48. http://dx.doi.org/10.1016/j.neunet.2008.09.015
- P. Bolzern, P. Colaneri and G. De Nicolao, “On Almost Sure Stability of Continuous-Time Markov Jump Linear Systems,” Automatica, Vol. 42, No. 6, 2006, pp. 983-988. http://dx.doi.org/10.1016/j.automatica.2006.02.007
- Z. Fei, H. Gao and P. Shi, “New Results on Stabilization of Markovian Jump Systems with Time Delay,” Automatica, Vol. 45, No. 10, 2009, pp. 2300-2306. http://dx.doi.org/10.1016/j.automatica.2009.06.020
- L. Huang, X. Mao and F. Deng, “Stability of Hybrid Stochastic Retarded Systems,” IEEE Transactions on Circuits and Systems I: Regular Papers, Vol. 55, No. 11, 2008, pp. 3413-3420. http://dx.doi.org/10.1109/TCSI.2008.2001825
- X. Mao, “Stability of Stochastic Differential Equations with Markovian Switching,” Stochastic Processes and their Applications, Vol. 79, No. 1, 1999, pp. 45-67. http://dx.doi.org/10.1016/S0304-4149(98)00070-2
- X. Mao and C. Yuan, “Stochastic Differential Equations with Markovian Switching,” Imperial College Press, London, 2006. http://dx.doi.org/10.1142/p473
- X. Mao, G. G. Yin and C. Yuan, “Stabilization and Destabilization of Hybrid Systems of Stochastic Differential Equations,” Automatica, Vol. 43, No. 2, 2007, pp. 264- 273. http://dx.doi.org/10.1016/j.automatica.2006.09.006
- C. Yuan and J. Lygeros, “On the Exponential Stability of Switching Diffusion Processes,” IEEE Transaction on Automatic Control, Vol. 50, No. 9, 2005, pp. 1422-1426. http://dx.doi.org/10.1109/TAC.2005.854641
- C. Yuan and J. Lygeros, “Stabilization of a Class of Stochastic Differential Equations with Markovian Switching,” Systems Control Letters, Vol. 54, No. 9, 2005, pp. 819-833. http://dx.doi.org/10.1016/j.sysconle.2005.01.001
- C. Yuan and G. Yin, “Stability of Hybrid Stochasti Delay Systems Whose Discrete Components Have a Large State Space: A Two-Time-Scale Approach,” Journal of Mathematical Analysis and Applications, Vol. 368, No. 1, 2010, pp. 103-119. http://dx.doi.org/10.1016/j.jmaa.2010.02.053
- Y. Yang, J. Li and G. Chen, “Finite-Time Stability and Stabilization of Nonlinear Stochastic Hybrid Systems,” Journal of Mathematical Analysis and Applications, Vol. 356, No. 1, 2009, pp. 338-345. http://dx.doi.org/10.1016/j.jmaa.2009.02.046
- L. Zhao and F. Xi, “Explicit Conditions for Asymptotic Stability of Stochastic Linard-Type Equations with Markovian Switching,” Journal of Mathematical Analysis and Applications, Vol. 348, No. 1, 2008, pp. 267-273. http://dx.doi.org/10.1016/j.jmaa.2008.07.030
- L. Liu and Y. Shen, “The Asymptotic Stability and Exponential Stability of Nonlinear Stochastic Differential Systems with Markovian Switching and with Polynomial Growth,” Journal of Mathematical Analysis and Applications, Vol. 391, No. 1, 2012, pp. 323-334. http://dx.doi.org/10.1016/j.jmaa.2012.01.058
- F. Wu and S. Hu, “Suppression and Stabilisation of Noise,” International Journal of Control, Vol. 82, No. 11, 2009, pp. 2150-2157. http://dx.doi.org/10.1080/00207170902968108
- X. Mao, “Exponential Stability of Stochastic Differential Equations,” Dekker, NewYork, 1994.
- L. Feng, Y. Shen and Z. Li, “Suppression of Functional System with Markovian Switching,” In: Lecture Notes in Computer Science 7664 of the 19th International Conference on Neural Information Processing, Springer, Doha, Qatar, 2012, pp. 460-466.

