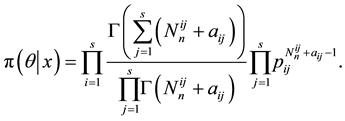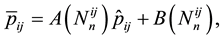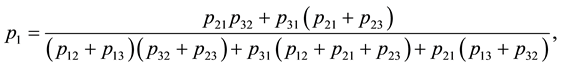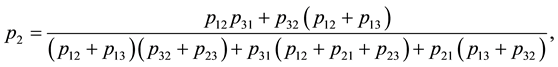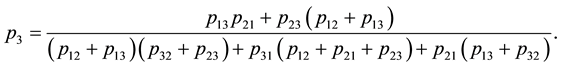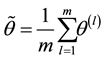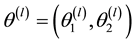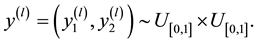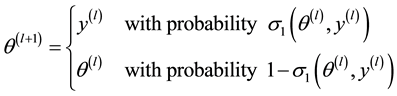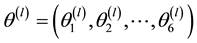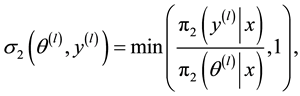Applied Mathematics
Vol.05 No.01(2014), Article ID:41613,7 pages
10.4236/am.2014.51006
Note on the Linearity of Bayesian Estimates in the Dependent Case
Souad Assoudou1, Belkheir Essebbar2
1Department of Economics, Faculty of Law, Economics and Social Sciences, Hassan I University, Settat, Morocco
2Department of Mathematics and Computer Sciences, Faculty of Science, Mohammed V University, Rabat, Morocco
Email: s_assoudou@yahoo.fr
Copyright © 2014 Souad Assoudou, Belkheir Essebbar. This is an open access article distributed under the Creative Commons At- tribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is prop- erly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Souad Assoudou, Belkheir Essebbar. All Copyright © 2014 are guarded by law and by SCIRP as a guar- dian.
ABSTRACT
Received September 21, 2013; revised October 21, 2013; accepted October 28, 2013
This work deals with the relationship between the Bayesian and the maximum likelihood estimators in case of dependent observations. In case of Markov chains, we show that the Bayesian estimator of the transition proba- bilities is a linear function of the maximum likelihood estimator (MLE).
Keywords:
Bayes Estimator; Maximum Likelihood Estimator; Markov Chain; Transition Probabilities; Jeffreys’ Prior; Multivariate Beta Prior; MCMC
1. Introduction
Let  be the random variable with Bernoulli distribution with parameter
be the random variable with Bernoulli distribution with parameter . It’s known that the Bayesian solution, under quadratic loss and a beta distribution
. It’s known that the Bayesian solution, under quadratic loss and a beta distribution 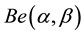 as prior for
as prior for , is given by
, is given by
 (1.1)
(1.1)
with  and
and . If
. If 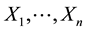 is a sample from
is a sample from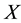 , the Bayesian estimate becomes
, the Bayesian estimate becomes
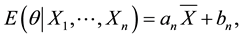 (1.2)
(1.2)
with  and
and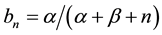 .
.
Moreover, 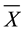 is the MLE which coincides with the empirical estimate.
is the MLE which coincides with the empirical estimate.
Formulas (1.1) and (1.2) are still true with distribution of 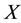 in the exponential family [1].
in the exponential family [1].
Let’s now move to the dependent case and show that (1.2) is still true for the Markov chains.
Let  be the
be the  first observations of an homogeneous Markov chain with a finite state space
first observations of an homogeneous Markov chain with a finite state space 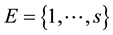 and let
and let  be the matrix of transition probabilities. The likelihood is
be the matrix of transition probabilities. The likelihood is
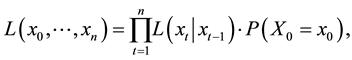 (1.3)
(1.3)
where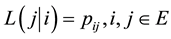 .
.
Let 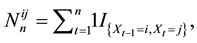
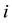
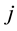

then (1.3) becomes
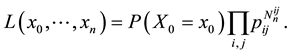
The parameter 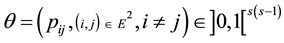
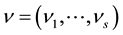
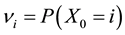
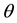

which coincides with the empirical estimate.
The Bayesian estimator under the quadratic error loss, is given by
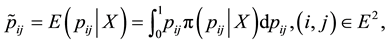
where 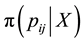
This work is organized as follows: In the second Section, we develop the Bayesian estimation for different priors. In Section 3, the cases of 2 and 3 states Markov chain are discussed. A numerical study is given in Section 4.
2. The Bayesian Framework
In this section, we introduce two conjugate prior distributions for 
2.1. Multivariate Beta Priors
Given the characteristics of the transition probabilities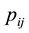


where 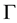
There are 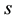

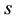
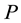
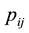
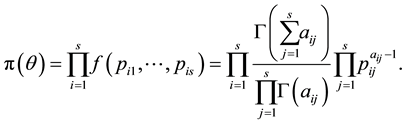
Making use of the likelihood given by (1.4) and the prior in (1.8), the joint posterior is
The Bayesian estimator of 
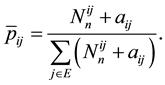
Let us remark that the Bayesian estimator 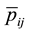
with 
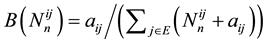
be compared to (1.2), but here, the coefficients 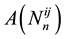
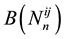
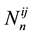
2.2. The Jeffreys’ Prior
Assoudou and Essebbar [3] have studied the Bayesian estimation for the multistate Markov chains, under the Jeffreys’ prior distribution. As shown, this prior has many advantages: it permits a certain type of dependence between the various transition probabilities. Moreover it’s a conjugate prior for 
The Jeffreys’ prior and the correspondent posterior distributions [3] are respectively given by
where 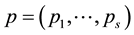

One can deduce the Jeffreys’ prior and posterior distributions for the two-states Markov chain,
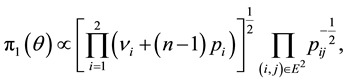
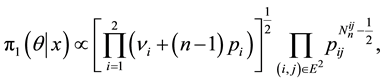
where 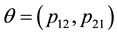

For the three-states Markov chain with parameter
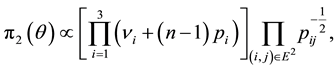
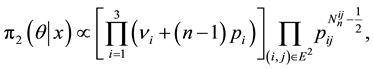
where the stationary probability 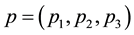
3. The Bayesian Solution
For either posterior distributions (1.11) or (1.13), the integral given by (1.6) is difficult to calculate, so we propose an approximation of it by mean of an algorithm, namely the Independent Metropolis-Hasting algorithm (IMH) [4].
The fundamental idea behind these algorithms is to construct an homogeneous and ergodic Markov chain 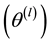
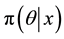
For 
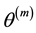
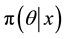

used to derive the posterior means. For instance, the Ergodic Theorem [4] justifies the approximation of the integral (1.6) by the empirical average
in the way that 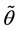

For next, we will give the description of this algorithm in the cases of two-states and three-states.
1) Case of the two-states Markov chain
Given
・ Step1. Generate
・ Step2. Take
where
・
・ 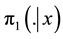
2) Case of the three-states Markov chain
Given
・ Step1. Generate 
1) Generate 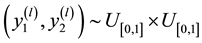
2) Generate 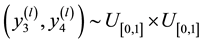
3) Generate 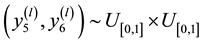
・ Step2. Take
where
・ 
4. Numerical Study
In order to characterize the relationship between the Bayesian estimator and the MLE, it’s indispensable to perform simulation studies. The first part of the analysis is devoted to Bayesian model founded on the multivariate beta prior given by (1.8) while the second deals with the Bayesian model using the Jeffreys’ prior given by theorem 1. We discuss through this analysis the cases of Markov chain with two and three states.
In both experiments, a pascal program is written to run the transition probabilities. The Bayesian estimator corresponding to Jeffreys’ prior is obtained from a single chain including 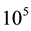
4.1. Experiment (a)
In Section 2.1, we have shown that, under the multivariate beta prior, the analytical Bayesian solution doesn’t express clearly a certain linearity of the MLE. In this experiment, we demonstrate by simulation that the Bayesian estimator given by (1.9) is a linear function of the MLE given by (1.5).
4.1.1. Case of the Two-States Markov Chain
The data set is composed of 100 independent two-states Markov chains with 20 observations. To generate this data set, transition probabilities for each chain are drawn from the beta prior given by (1.8) with 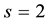
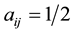

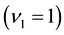
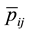
Figure 1(a) (resp. Figure 2(a)) shows the plot of 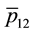
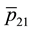

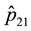
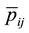
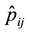
4.1.2. Case of the Three-States Markov Chain
In this experiment we generate 100 independent Markov chains each with three states and 60 observations. By using the IMH algorithm, the transition probabilities are simulated from the multivariate beta given by (1.8) with 
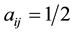
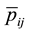
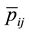
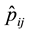
4.2. Experiment (b)
Now let us consider the Bayesian model based on the Jeffreys’ prior such that described in Section 2.2.
4.2.1. Case of the Two-States Markov Chain
In this experiment, we simulate 100 independent two-states Markov chains with
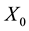
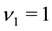
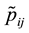

Figure 1(b) (resp. Figure 2(b)) displays the plot of 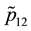
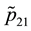
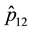
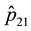
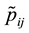
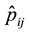
4.2.2. Case of the Three-States Markov Chain
The same experiment is repeated once more, but now the transition probabilities are drawn from the Jeffreys’ prior given by (1.12) in order to gererate 100 independent three-states Markov chains with
The next figures (Figure 3(b) until Figure 8(b)) show the plots of 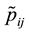
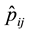
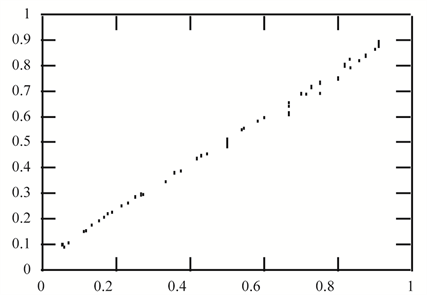
Figure 1. (a) Plot of 
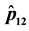
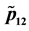
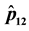
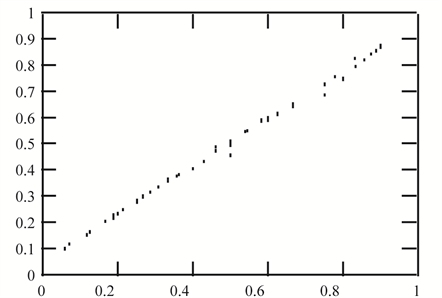
Figure 2. (a) Plot of 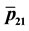
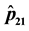
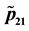
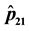

Figure 3. Plot of 
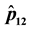
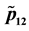
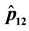

Figure 4. (a) Plot of 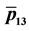
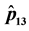
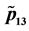
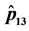
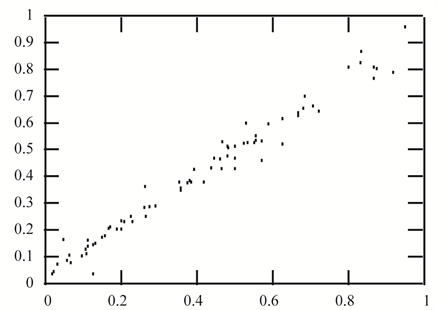
Figure 5. (a) Plot of 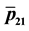
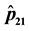
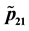
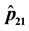

Figure 6. (a) Plot of 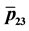
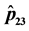
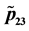
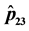
5. Conclusion
The objective of this work is to study the relationship between the Bayesian estimator and the MLE in a dependent case such as a Markov chain. A numerical study by simulation is carried out to describe the nature of this relationship. Under the multivariate beta and the Jeffreys’ priors we have shown that the Bayesian solution is still a linear function of the MLE. This linearity is now verified by simulation for these two models, others

Figure 7. (a) Plot of 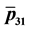
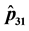
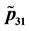
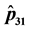

Figure 8. (a) Plot of 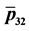
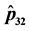
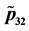
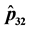
simulation will be developed for different Bayesian models. The next step will be to proof analytically this property.
References
- P. Diaconis and D. Ylvisaker, “Conjugate Priors for Exponential Families,” The Annals of Statistics, Vol. 7, No. 2, 1979, pp. 269-281.
- T. C. Lee, G. G. Judge and A. Zellner, “Maximum Likelihood and Bayesian Estimation of Transition Probabilities,” JASA, Vol. 63, No. 324, 1968, pp. 1162-1179.
- S. Assoudou and B. Essebbar, “A Bayesian Model for Markov Chains via Jeffreys’ Prior,” Department of Mathematics and Computer Sciences, Faculté des Sciences of Rabat, Morocco, 2001.
- C. Robert, “Méthode de Monte Carlo par Chanes de Markov,” Economica, Paris, 1996.