Applied Mathematics
Vol.4 No.10A(2013), Article ID:37403,5 pages DOI:10.4236/am.2013.410A1006
On the Metaheuristics Approach to the Problem of Genetic Sequence Comparison and Its Parallel Implementation
1Department of Mathematics and Information Science, Togliatti State University, Togliatti, Russia
2Togliatti Branch of Samara State University, Togliatti, Russia
3Yandex Company, Moscow, Russia
Email: S.Makarkin@gmail.com, bormel@rambler.ru, AG.Panin@gmail.com
Copyright © 2013 Sergey Makarkin et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received August 2, 2013; revised September 2, 2013; accepted September 9, 2013
Keywords: Metaheuristic Approach; Genetic Sequence Analysis; Levenshtein Distance; Strings Alignment; Parallel Programming
ABSTRACT
We describe parallel implementation of the metaheuristic approach to the problem of comparing strings representing DNA sequence. By this approach, one can define a whole new class of metrics on a set of strings; some of this metrics can lead to interesting results when used for string comparison. We propose several heuristics; compare results achieved when using those heuristics and compare parallel and sequential implementation of proposed approach.
1. Introduction
Determining DNA likeness is a particular case of a more common task of approximate comparison of strings, although called fuzzy comparison [1]. “Fuzzy” means here, which we should be able to determine similar sequences even if there are some errors and distortions, like insertion or deletion of several symbols. The amount of such distortions can be used as a metrics on a set of strings, defined as the minimum number of edits needing to transform one string into the other. This task can be found in many areas, like comparison of genes, chromosomes and proteins, which are one of the most important problems and at the same time one of the basic tools in molecular biology and bioinformatics [1,2]. Strict comparison of chains of nucleotides is unacceptable because of errors in data and possibility of mutations. Although the fuzzy comparison is used in text processing, Levenshtine metrics is used for error correction, for improvement of text recognition quality and in database search [1].
There are several approaches used for string comparison. Algorithms based on dynamic programming (like Hunt-Shimansky, Khirshberg, Wagner-Fisher and other) can provide the exact solution ([1,3-6]). Mostly, such algorithms have quadratic worst-case complexity and are considered too slow when speed is more important than accuracy (like database search). There are many approximate algorithms designed especially for some field of science, like BLAST [7] algorithm, designed for genetic database search.
Metaheuristic approach to fuzzy string comparison was firstly described in [8]. The strings likelihood assertion made by this approach is close to Levenshtein distance, but it is not equal to, nor is an approximation of Levenshtine distance. This algorithm allows using multiple alternative metrics on space of chains of nucleotides, depending on used heuristics. This metrics can reflect the likelihood of compared strings, although they show different meanings of likelihood itself.
2. Implementing Metaheuristic Approach
Meta-heuristic approach to discrete optimization problems uses branch and bound algorithm combined with several different heuristics that are used for next step selection. Heuristics assessments are averaged using dynamical risk functions. Genetic algorithms are used to fit the averaging ratios, the same genetic algorithms with simplified self-learning are used for branch and bound startup ([9,10]).
For this particular problem we did the following. Let x, y be the source strings, i, j be indexes of symbol in x and y, respectively, r be metrics value. By shift of a string we mean increasing appropriate index by 1. The algorithm is described by the following:
Input: Strings x and y.
Step 1: i: = 0, j: = 0, r: = 0;
Step 2: if x [i] = y [j] then begin Shift both strings;
r: = r + cost of matching x [i] and y [j];
end
else begin
apply heuristics to generate possible “trajectories” to shift into i' and j' such, that x [i'] = y [j'];
rate trajectories with some other heuristics;
apply risk function to average ratings;
perform a shift (possibly updating r);
end;
Step 3: repeat step 2 until the end of one of the strings is reached.
The cost of matching two symbols in a simplest case equals to 1; for DNA it can be defined using some table of amino acid replacement costs, e.g. BLOSUM [11].
The following heuristics were used:
1) We select such trajectories that the value (i' − i) + (j' − j) is minimum, or close to minimum. E.g. we first lookup all the trajectories with one string shifted by one symbol; next with one string shifted by two symbols or both strings shifted by one symbol, etc.
2) We shift a string, which current symbol found less frequent in the other string. For this heuristics it’s preferable to know probabilities of appearance of a given symbol in each of the strings. If those probabilities are not known a priori, we consider them being equal. While following the algorithm we can adjust those probabilities or use aging algorithm, such that probability of a given symbol will be defined by some fragment of a string instead of a whole string. If probabilities for both strings are equal, we shift a string in which more symbols are left.
3) Combination of previous heuristics (1 and 2); to calculate the position using second heuristics we sum probabilities of finding other string for all symbols that will be passed by a shift.
4) Use of an algorithm of a longest common subsequence search for x [i..i + k] and y [j..j + k], where k ~ 15. For shift we use i', j', at which the longest common subsequence ends. If no common subsequence found, the search range is increased. When using this heuristics the result is close to the longest common subsequence value.
5) Combination of 3 and 4; the position (i', j') given by forth heuristics is a ratio of length of the longest common subsequence of strings x [i..i'] and y [j..j'] to an average shift length from (i, j) to (i', j').
6) We use algorithm [10] for strings x [i..i + k] and y [j..j + k], where k ~ 15, then shift to (i', j'), having the greatest value in Needleman-Wunsch table.
Combination of 3 and 6; the position (i', j') given by sixth heuristics is a ratio of a value in NeedlemanWunsch table, corresponded to that position, to average shift length from (i, j) to (i', j').
3. Using Multiple Greedy Heuristics
Now let us consider heuristics used to select the element that separates the problem into right and left sub-problems for branch and bounds method. Solving a discrete optimization problem by branch and bounds method, it is desirable to choose separating algorithms depending on the solved sub-problem. Separating algorithms can be selected based on dimension of the solved problem, its bound, and by taking into account some specific characteristics of considered problem.
In classical examples of branch and bounds method for travelling salesman problem ([12] etc.), some good separating algorithms were used (by “good” we mean that they perform better than other ones). However, long before [12], various other heuristics were used for the branching, see, e.g., [13] Let us mention, for example, the following heuristics for the reduced TSP-matrix: total number of zeroes, sum of minimums for all the rows and columns, sum of some minimum values of considered row and columns multiplied by special “dam-nation constants”; all these values are computed by the TSP-matrix after reducing and selecting separating element (i.e., separating edge for branching). Probably we mentioned here less than 10% of the heuristics used before.
Thus, how can we use the fact that in different situations (i.e., in different sub-problems of the same discrete optimization problem) different heuristics relatively perform better? (This question is true for both exact and unfinished algorithms). We need decide which separating element to use for branching. We have information from various experts, i.e., of various special heuristics, so called predictors (or estimators). The predictors often give discrepant information, and we have to average it in some special way. We use an approach that is used in nondeterministic games programming: dynamic risk functions.
Since different heuristics return values of different measurement units, we have to normalize them for computing the final result. For that purpose one can use a special set of normalizing coefficients. The other possible solution is a modification of “voting method”: use special dynamic risk functions for the results of voting. It is important to note, that the dynamic selection of the particular risk function is similar to selecting it in nondeterministic games programming ([14,15]). Since we consider here discrete optimization problems (not nondeterministic games programming), we have to add here new heuristics, i.e. heuristics for selecting “current position estimation”, in other words, for evaluation of the situation obtained by the solving some discrete optimization problem using branch and bounds method.
Thus, let us have some various heuristics for selecting next step element of branch and bounds method (or, generally speaking, for selecting the strategy of solving). Let each of possible strategies have some various expert evaluations of availability (i.e., let us have some independent expert sub-algorithms, so called predictors). Then the concluding strategy could be chosen by maximum of average values. However, let us consider the following example; this example is connected with backgammon programming, because it uses 36 predictors).
Let expert evaluations of availability lie in segment [0,1]. Let the 1st expert evaluation of availability for the 1st strategy be equal to 1, and evaluations of 35 other experts be equal to 0.055. And for the 2nd strategy, 2 experts have evaluation equal to 0.95, and other 34 experts have evaluation equal to 0. It is very likely that each human expert in such case will choose 2nd strategy. However, averaging-out by the simplest algorithm (i.e. simple average of expert evaluations) gives 0.081 for the 1st case and 0.053 for the 2nd one; so do we have to choose the 1st strategy?
On the other hand, we can use an approach similar to [15], i.e., use the same algorithms for dynamic risk function construction. For the 1st strategy, we obtain the following risk function:
–0.685·x2 + 1.300·x + 0.386;
and for the 2nd strategy:
–0.694·x2 + 1.374·x + 0.321.
The final values of expert evaluations averaging-out by using these risk functions are 0.111 for the 1st strategy and 0.147 for the 2nd strategy. Therefore, using such algorithms for dynamic risk function construction for expert evaluations averaging-out gives “natural” answers.
Note that repeating the averaging procedure twice (i.e., averaging-out using preliminary values of the first step of dynamic risk functions) chooses 1st strategy. However, in the limit we have “natural” answers again. This can be seen in Table 1; the column headers are equal to the number of step of averaging-out using dynamic risk function (i.e., the number of iterations ran by a dynamic risk function constructing algorithm). The column 0 is the simple average of expert evaluations, and the column ¥ is the limit value.
Note that in real discrete optimization problems such situations, when the difference between minimum and maximum values is more than 0.5 (i.e., more than 50% of the segment of values) are very often; for example, for accidental TSP having dimension 75 and some of predictors mentioned before, they contain, by statistics of
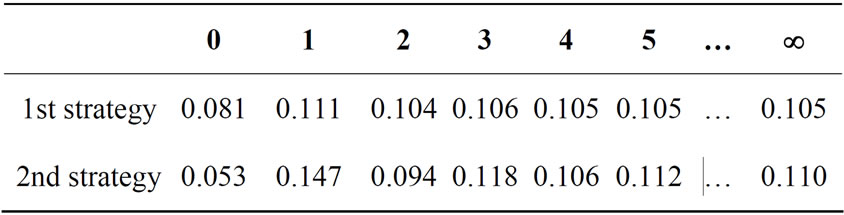
Table 1. Risk function values for different strategies.
the author, about 10%.
4. Approach to a Parallel Algorithm
Main problem in parallel algorithm design is finding informational dependencies and independent sub-tasks.
The proposed algorithm is based on iterative shift of strings in some position, defined by two indexes (i, j) for first and second string respectively. To define next step we search in some small set of positions, closest to current one, and then we select the position with the highest score. Obviously, such shifts can be made only sequentially, and the only part of an algorithm that has independent subtasks is a usage of heuristics for position selection. There are two possible ways for parallelizing this subtask: applying each heuristics in separate thread, and using parallel algorithms for heuristics themselves.
Using separate threads for each heuristics has the following disadvantages. First, the final result of using several heuristics is not always their “linear sum”, sometimes several heuristics are combined and considered as one complex heuristics. Second, some heuristics have relatively low computational complexity, and thread management costs become too significant.
Parallelizing heuristics although has disadvantages. Some heuristics being parallelized work slower, then their serial analogues, because of high overhead costs (like mentioned above thread management costs).
Thereby selecting independent subtasks seems not to be effective enough for practical use. But this does not mean that it is impossible to create effective parallel algorithm, because one can define some new subtasks. Thereto at each step we can select multiple possible shift positions, creating several “phase trajectories” in shift position space. There are several ways to do that, e.g. use several positions with highest score or use some ad hoc heuristics. Subtasks created like this can have a fixed size (i.e. iterations of basic shift cycle). After processing subtasks we can select several best results and generate new subtasks based on them.
Parallel implementation of meta-heuristic approach described above is a new algorithm, and introduced method of subtasks creation is basically, a new heuristics. This new parallel algorithm has better results than the sequential one, it is more precise. While the initial algorithm uses greedy heuristics to select next shift position, the introduced algorithm make deeper analysis of consequences of next step selection.
5. Results of DNA Comparison
To test our algorithm, we used mitochondrial DNA of different organisms. Those DNA molecules containing in cell’s mitochondria are not recombined, and they are inherited from mother’s organism by most of multicellular organisms. Therefore they can be changed only due to mutations. By analyzing mitochondrial DNA and its mutations, one can determine not only the degree of kinship of two species, but although a time, needed to accumulate some mutations in population [16]. Thereby one can estimate a moment of time when there were no mutations and population was genetically homogeneous.
We used genetic data for next species: Homo sapiens (human), Pan troglodytes (chimpanzee), Bison bison (bison), Bos taurus (wild bull), Sus scrofa taiwanensis (pig), Canis lupus (wolf), Felis catus (domestic cat), Gallus gallus (chicken), Mus musculus (mouse), Rattus norvegicus (rat), Orcinus orca (killer whale), Orcaella brevirostris (Irrawaddy dolphin), Peponocephala electra (melon-headed whale), Gadus morhua (Atlantic cod), Drosophila simulans (see [17]). An example of DNA comparison results are presented in Table 2.
After analyzing test results we have made the following conclusions: First two heuristics show insignificant differences for all compared pairs of DNA. However this does not mean that the underlying principals are wrong, because the third heuristics, which based on the former two, showed adequate results, pretty close to the results showed by longest common subsequence search. Thus
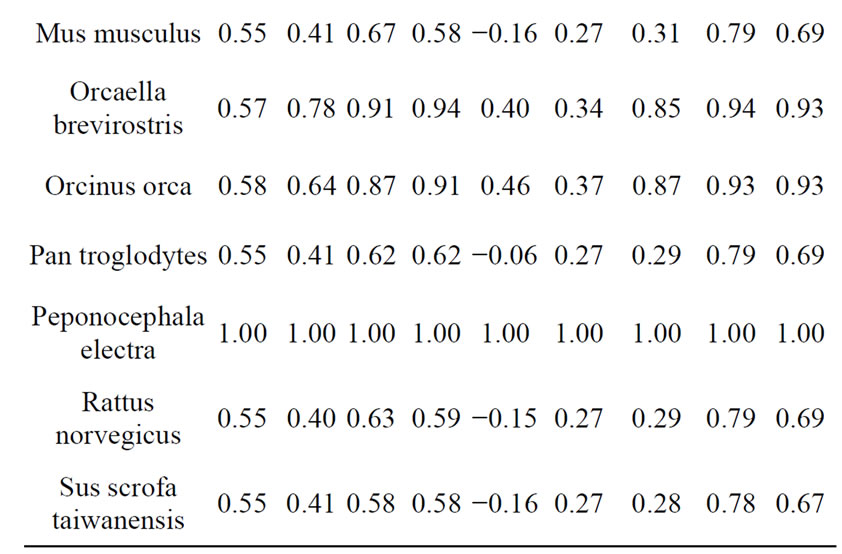

Table 2. Results of comparison Peponocephala electra with other species.
the kinship rate for Irrawaddy dolphin and melon-headed was 0.91, Irrawaddy dolphin and a killer whale were 0.87, Irrawaddy dolphin and other Chordata were 0.59 to 0.63, Irrawaddy dolphin and Drosophila were 0.45. Results shown by the forth heuristics are pretty similar to those of the third one. Fifth heuristic showed pretty similar results, but feebly marked for small values. Results shown by sixth heuristics do not allow to mate any conclusion about DNA kinship. Seventh heuristics (that is a combination of third and sixth one) showed results pretty similar to Needlemah-Wulsch algorithm. For big values (more than 0.9) seventh heuristics results differing from Needleman-Wulsch were not more than 1%.
Results shown by parallel version of algorithm showed the same results, but shifted to a high values range. Parallel implementation of fifth heuristics performed better than sequential one, and was closer to results showed by the longest common subsequence search algorithm. On the contrary, results of parallel implementation of the seventh heuristic performed poor, and showed obviously wrong results for some DNA pairs. In [10] we had already covered an approach to parallelizing branch-andbouds algorithms, and here we used the same approach with heuristics. The results of that research contain lots of data and can’t be presented here, so it will be described in a separate paper.
For most of heuristics the results of DNA comparison correspond to biological taxonomy [18]. At the same time the proposed algorithms are pretty fast, because the run time is in linear dependence with input length, but depends on heuristics parameters. This makes the proposed algorithms applicable for DNA data analysis.
REFERENCES
- D. Gusfield, “Algorithms on Strings, Trees and Sequences,” Informatics and Computers, BHV-Peterburg, Saint-Petersburg, 2003.
- I. Torshin, “Bioinformatics in the Post-Genomic Era: The Role of Biophysics,” Nova Publishers, 2006.
- D. S. Hirschberg, “A Linear Space Algorithm for Computing Maximal Common Subsequences,” Communications of the ACM, Vol. 18, No. 6, 1975, pp. 341-343. http:dx.doi.org/10.1145/360825.360861
- J. W. Hunt and T. G. Szymanski, “A Fast Algorithm for Computing Longest Common Subsequences,” Communications of the ACM, Vol. 20, No. 5, 1977, pp. 350-353. http:dx.doi.org/10.1145/359581.359603
- E. W. Myers, “An Overview of Sequence Comparison Algorithms in Molecular Biology,” 1991.
- R. A. Wagner and M. J. Fischer, “The String-to-String Correction Problem,” Journal of the ACM, Vol. 21, No. 1, 1974, pp. 168-173. http:dx.doi.org/10.1145/321796.321811
- G. Wieds, “Bioinformatics Explained: BLAST versus Smith-Waterman,” CLCBio, 2007.
- A. Panin, “Using Metaheuristic Approach for DNA Comparison,” Vector of Science TSU, Vol. 3, No. 17, 2011, pp. 27-29.
- B. Melnikov, “Discrete Optimization Problems. Some New Heuristic Approaches,” 8th International Conference on High Performance Computing and Grid in Asia Pacific Region, IEEE Computer Society Press, 2005, pp. 73-80. http:dx.doi.org/10.1109/HPCASIA.2005.34
- B. Melnikov, “Multiheuristic Approach to Discrete Optimization Problems,” Cybernetics and Systems Analysis, Vol. 42, No. 3, 2006, pp. 335-341. http://dx.doi.org/10.1007/s10559-006-0070-y
- S. Henikoff and J. G. Henikoff, “Amino Acid Substitution Matrices from Protein Blocks,” PNAS, Vol. 89, No. 22, 1992, pp. 10915-10919. http:dx.doi.org/10.1073/pnas.89.22.10915
- J. Hromkovič, “Algorithms for Hard Problems. Introduction to Combinatorial Optimazation, Randomization, Approximation, and Heuristics,” Springer, Berlin, 2003.
- M. Bellmore and G. Nemhauser, “The Traveling Salesman Problem: A Survey,” Operation Research, Vol. 16, No. 3, 1968, pp. 538-558. http:dx.doi.org/10.1287/opre.16.3.538
- B. Mel’nikov and A. Radionov, “A Choice of Strategy in Nondeterministic Antagonistic Games,” Programming and Computer Software, Vol. 24, No. 5, 1998, pp. 247-252.
- B. Melnikov, “Heuristics in Programming of Nondeterministic Games,” Programming and Computer Software, Vol. 27, No. 5, 2001, pp. 277-288. http://dx.doi.org/10.1023/A:1012345111076
- A. C. Wilson, R. L. Cann, S. M. Carr, M. George Jr., U. B. Gyllensten, K. Helm-Bychowski, R. G. Higuchi, S. R. Palumbi, E. M. Prager, R. D. Sage and M. Stoneking, “Mitochondrial DNA and Two Perspectives on Evolutionary Genetics,” Biological Journal of the Linnean Society, Vol. 26, No. 4, 1985, pp. 375-400. http:dx.doi.org/10.1111/j.1095-8312.1985.tb02048.x
- NCBI Nucleotide Database. http:www.ncbi.nlm.nih.gov/nuccore
- A. Shipunov, “Systema Naturae or the Outline of Living World Classification,” Protistology, Vol. 6, No. 1, 2009, pp. 3-13.

