Applied Mathematics
Vol.4 No.8(2013), Article ID:35326,12 pages DOI:10.4236/am.2013.48153
Two-Sided First Exit Problem for Jump Diffusion Processes Having Jumps with a Mixture of Erlang Distribution*
School of Mathematical Sciences, Qufu Normal University, Qufu, China
Email: #wenyzhen@163.com, ccyin@mail.qfnu.edu.cn
Copyright © 2013 Yuzhen Wen, Chuancun Yin. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received May 29, 2013; revised June 29, 2013; accepted July 7, 2013
Keywords: First Exit Time; Two-Sided Jumps; Jump Diffusion Process; Overshoot
ABSTRACT
In this paper, we consider the two-sided first exit problem for jump diffusion processes having jumps with rational Laplace transforms. We investigate the probabilistic property of conditional memorylessness, and drive the joint distribution of the first exit time from an interval and the overshoot over the boundary at the exit time.
1. Introduction
Consider the following jump diffusion process
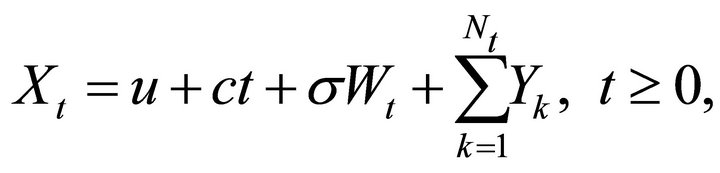 (1.1)
(1.1)
where the constant 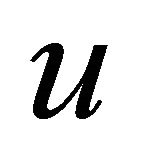 is the starting point of
is the starting point of ,
,  and
and  represent the drift and the volatility of the diffusion part, respectively,
represent the drift and the volatility of the diffusion part, respectively, 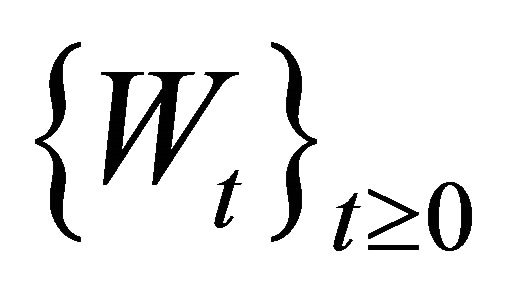 is a standard Brownian motion with
is a standard Brownian motion with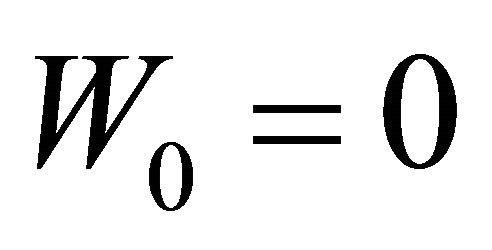 ,
,  is a Poisson process with rate
is a Poisson process with rate , and the jumps sizes
, and the jumps sizes 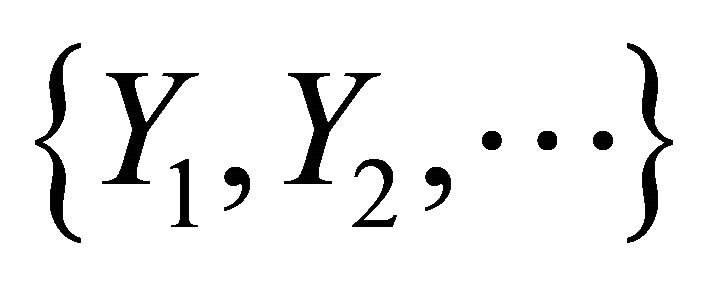 are assumed to be i.i.d. real valued random variables with common density
are assumed to be i.i.d. real valued random variables with common density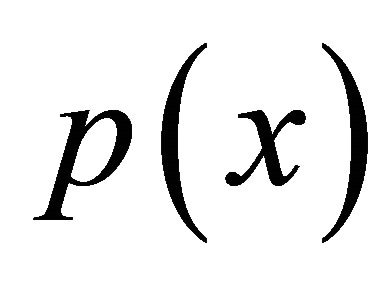 . Moreover, it is assumed that the random processes
. Moreover, it is assumed that the random processes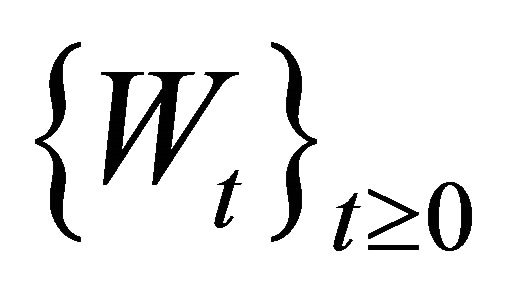 ,
, 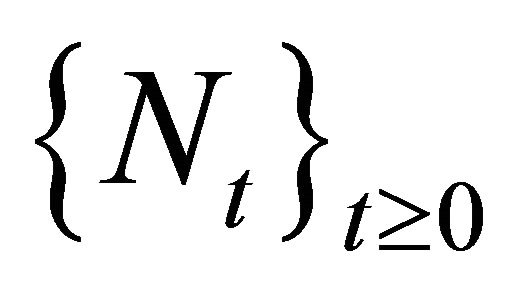 and random variables
and random variables 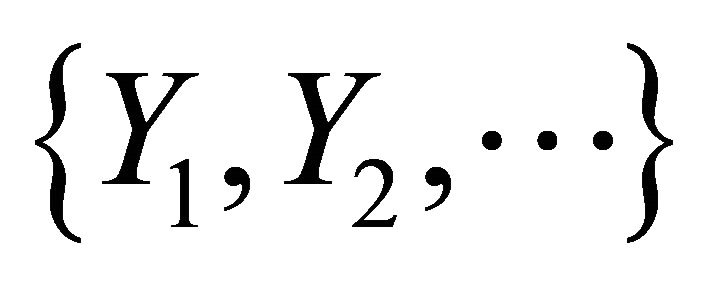 are mutually independent. In this paper we are interested in the density
are mutually independent. In this paper we are interested in the density 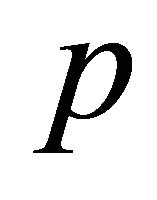 of following type
of following type
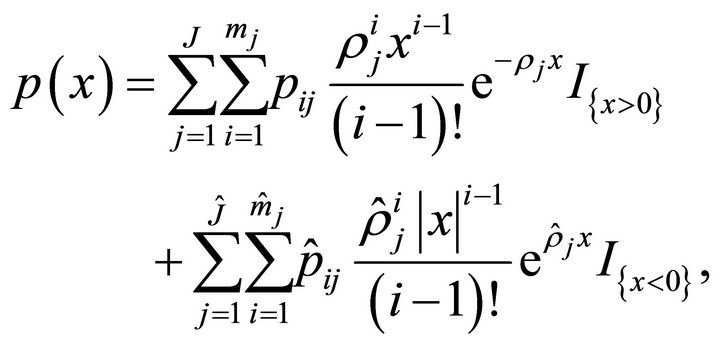 (1.2)
(1.2)
where ,
,  ,
,  ,
, 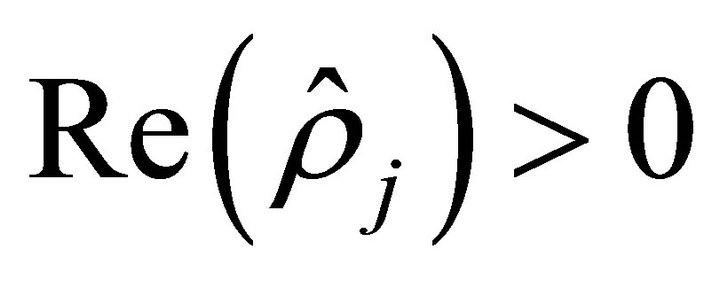 and that
and that ,
, 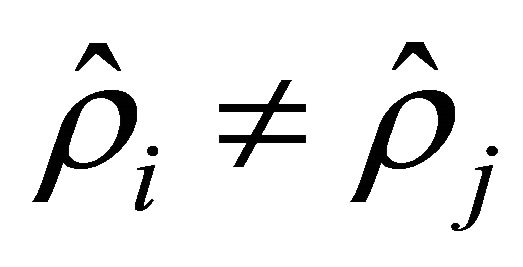 for all
for all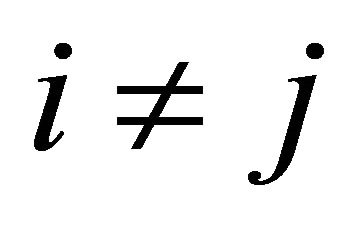 . Moreover,
. Moreover,

Define  to be the first exit time of
to be the first exit time of  to two flat barriers
to two flat barriers  and
and 
 , i.e.
, i.e.

Recently, one-sided and two-sided first exit problems for processes with two-sided jumps have attracted a lot of attentions in applied probability (see [1-7]). For example, Perry and Stadje [1] studied two-sided first exit time for processes with two-sided exponential jumps; Kou and Wang [2] studied the one-sided first passage times for a jump diffusion process with exponential positive and negative jumps. Cai [3] investigated the first passage time of a hyper-exponential jump diffusion process. Cai et al. [4] discussed the first passage time to two barriers of a hyper-exponential jump diffusion process. Closed form expressions are obtained in Kadankova and Veraverbeke [5] for the integral transforms of the joint distribution of the first exit time from an interval and the value of the overshoot through boundaries at the exit time for the Poisson process with an exponential component. For some related works, see Perry et al. [8], Cai and Kou [9], Lewis and Mordecki [10] and the references therein.
Motivated by works mentioned above, the main objective of this paper is to study the first exit time of the process (1.1) with jump density (1.2) from an interval and the overshoot over the boundary at the exit time. In Section 2, we study the roots of the generalized Lundberg equation and conditional memory lessness. The main results of this paper are given in Section 3.
2. Preliminary Results
It is easy to see that the infinitesimal generator of 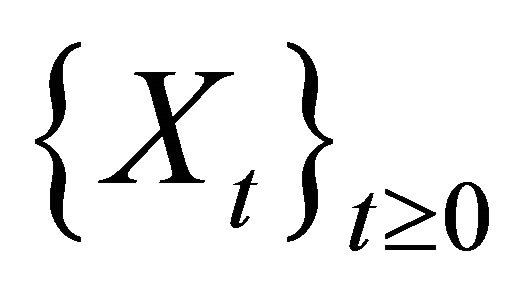 is given by
is given by
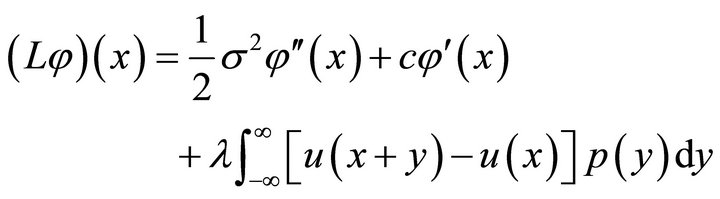
for any twice continuously differentiable function  and the Lévy exponent of
and the Lévy exponent of  is given by
is given by
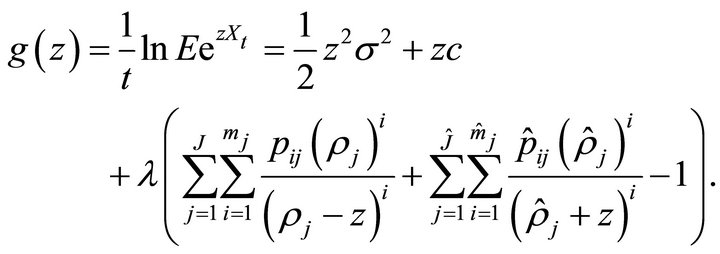
By analytic continuation, the function 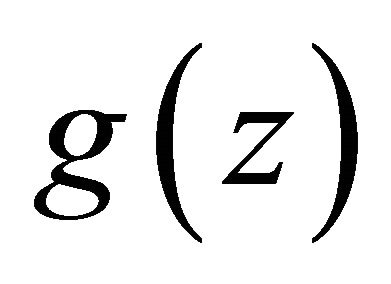 can be extended to the complex plane except at finitely many poles. In the following, we consider the resulting extension
can be extended to the complex plane except at finitely many poles. In the following, we consider the resulting extension 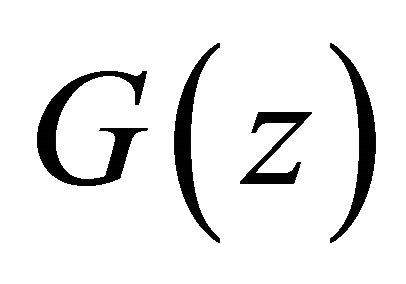 of
of , i.e.,
, i.e.,

Let us denote 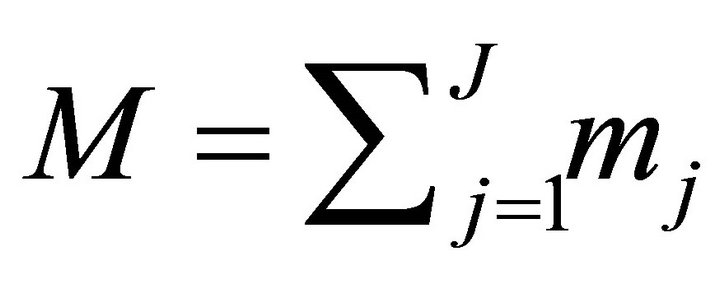 and
and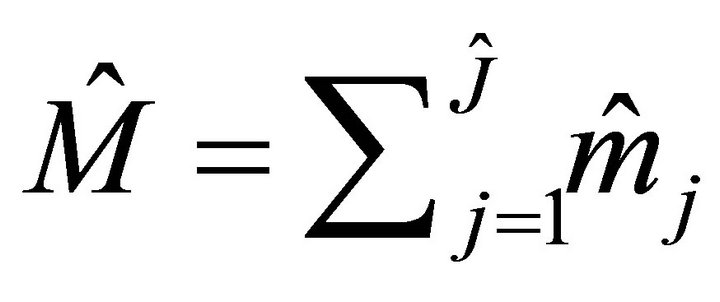 .
.
In [11], Kuznetsov has studied the roots of the equation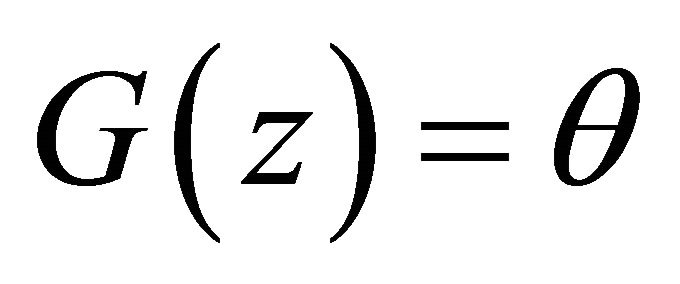 . However, for this particular Lévy process
. However, for this particular Lévy process , we will give another simple proof for the roots of this equation.
, we will give another simple proof for the roots of this equation.
Lemma 2.1. For fix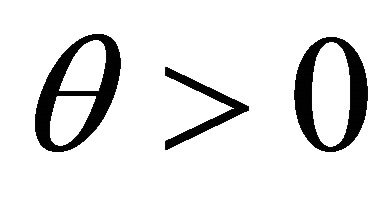 , the generalized CramérLundberg equation
, the generalized CramérLundberg equation

has 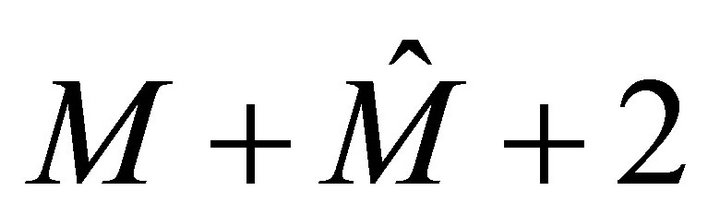 complex roots
complex roots  with
with 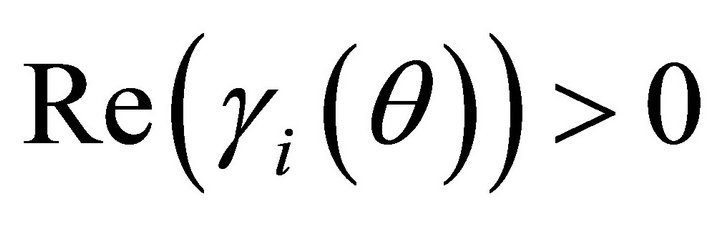 for
for  and
and 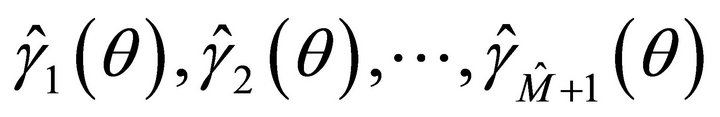 with
with 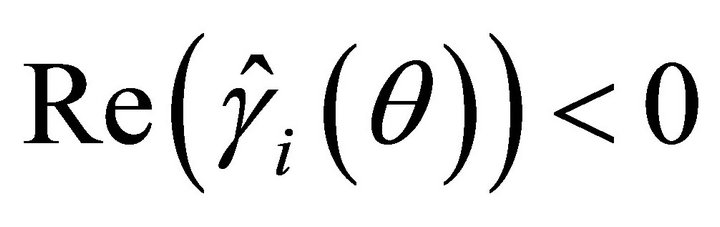 for
for .
.
Proof. Let
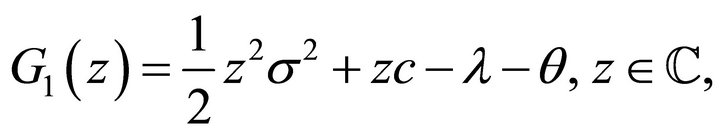
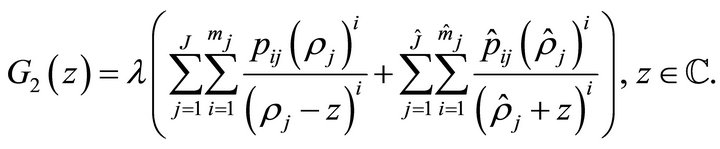
Firstly, we prove that for given ,
, 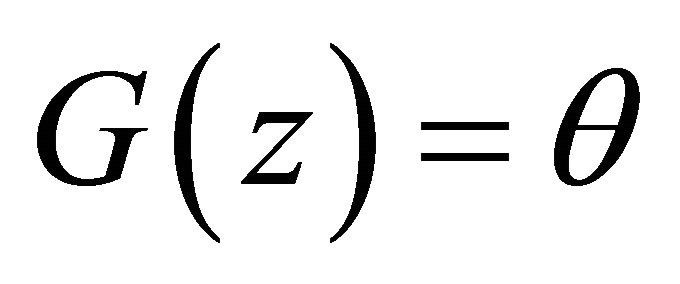 has
has 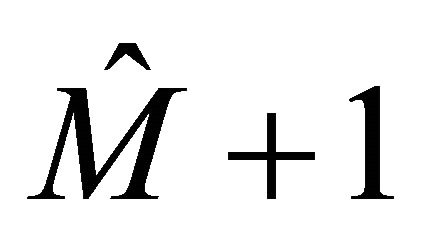 roots with negative real parts. Set
roots with negative real parts. Set
 with
with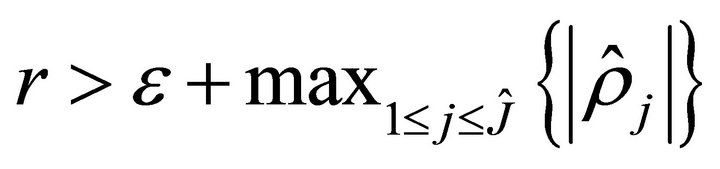 where
where  is an arbitrary positive constant. Applying Rouchés theorem on the semi-circle
is an arbitrary positive constant. Applying Rouchés theorem on the semi-circle , consisting of the imaginary axis running from
, consisting of the imaginary axis running from  to
to  and with radius
and with radius 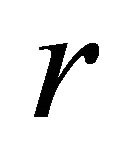 running clockwise from
running clockwise from 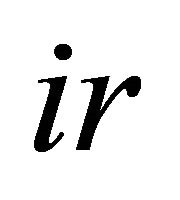 to
to . We let
. We let  and denote by
and denote by  the limiting semi-circle. It is known that both
the limiting semi-circle. It is known that both  and
and 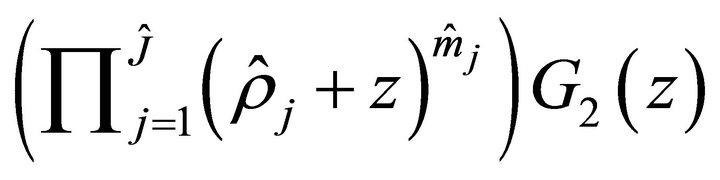 are analytic in
are analytic in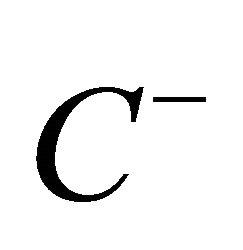 . We want to show that
. We want to show that

Notice that  for
for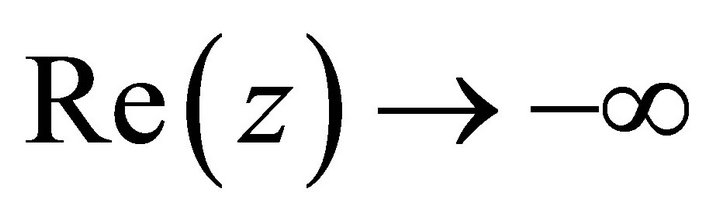 , and
, and
 is bounded for
is bounded for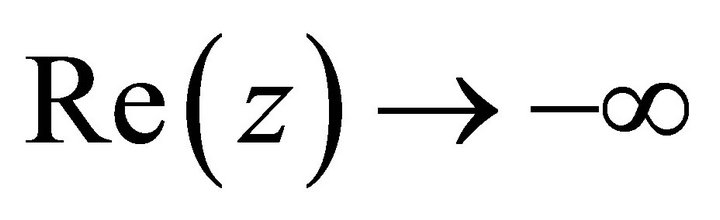 . Hence, for
. Hence, for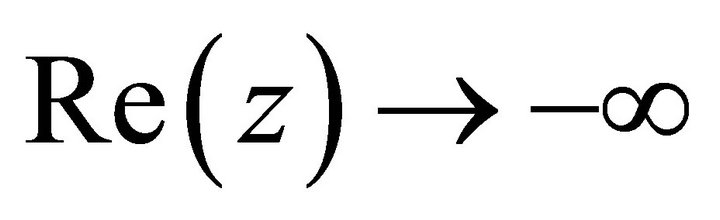 ,
,

on the boundary of the half circle in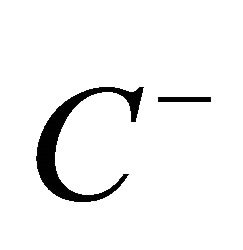 . For
. For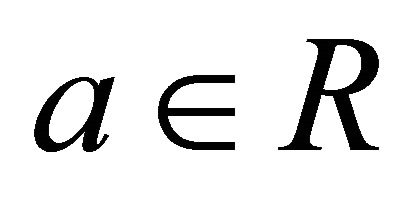 , we have
, we have 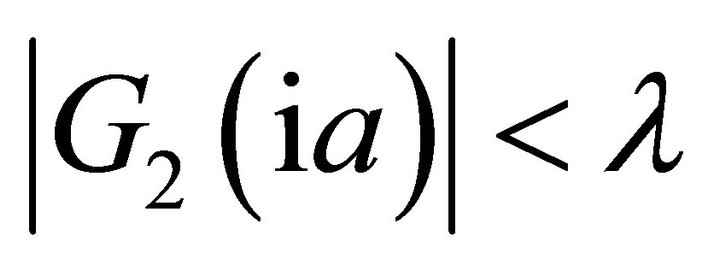 (see Lewis and Mordecki [10]). On the other hand,
(see Lewis and Mordecki [10]). On the other hand,
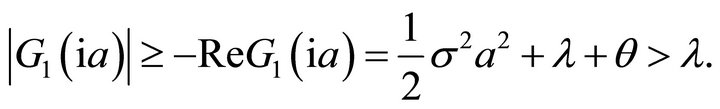
Thus we have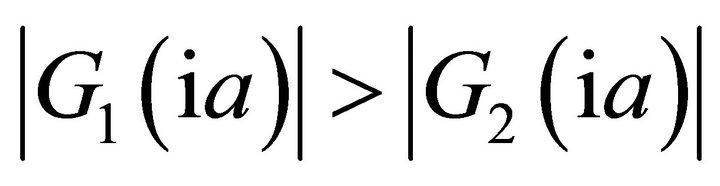 . Since
. Since
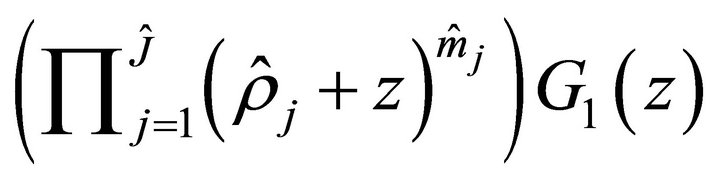 has
has 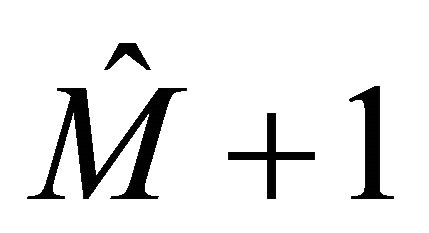 roots with negative real parts, so equation
roots with negative real parts, so equation 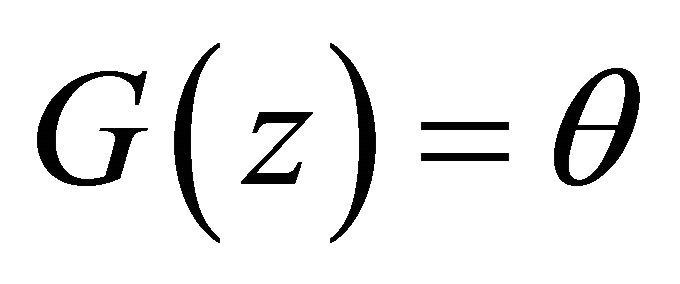 has
has 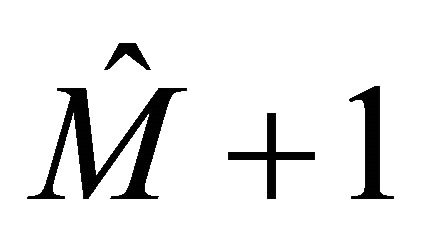 roots with negative real parts. Similarly, we can prove
roots with negative real parts. Similarly, we can prove  has
has 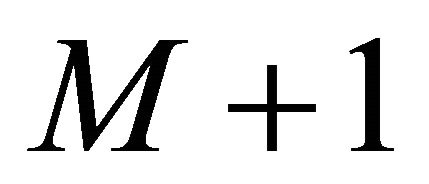 roots with positive real parts.
roots with positive real parts.
In the rest of this paper, we assume all the roots of equation  are distinct and denote
are distinct and denote  ,
,  for notational simplicity, and denote
for notational simplicity, and denote 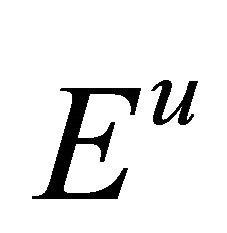 (or
(or 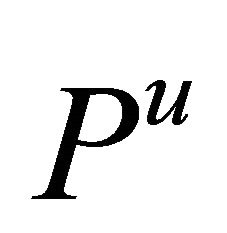 in the sequel) representing the expectation (or probability) when
in the sequel) representing the expectation (or probability) when 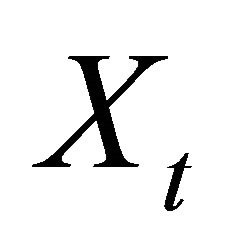 starts from
starts from . We denote a sequence of events
. We denote a sequence of events
 ,
, 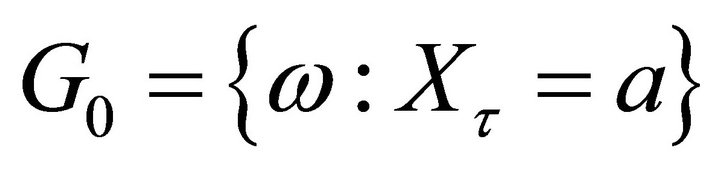
 = {
= { :
: 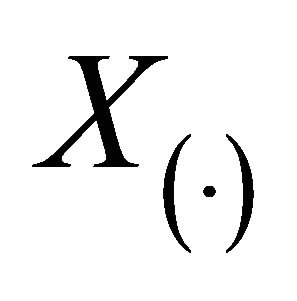 crosses
crosses  at time
at time  by the
by the  th phase of
th phase of  th positive jump whose parameter is
th positive jump whose parameter is 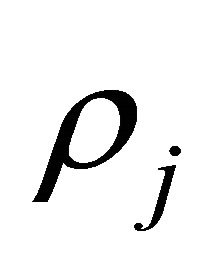 },
},
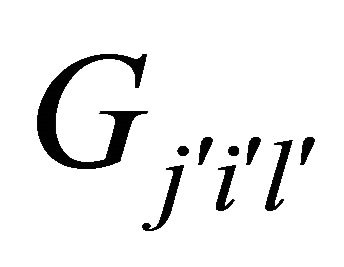 = {
= { :
:  crosses
crosses  at time
at time  by the
by the  th phase of
th phase of  th negative jump whose parameter is
th negative jump whose parameter is 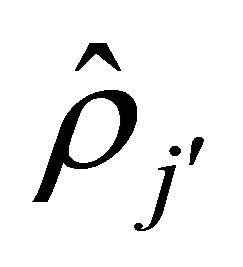 }
}
for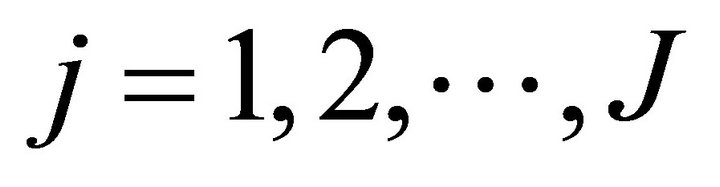 ,
,  ,
, 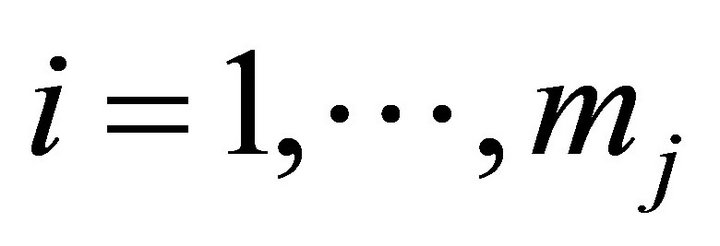 ,
,  ,
,  and
and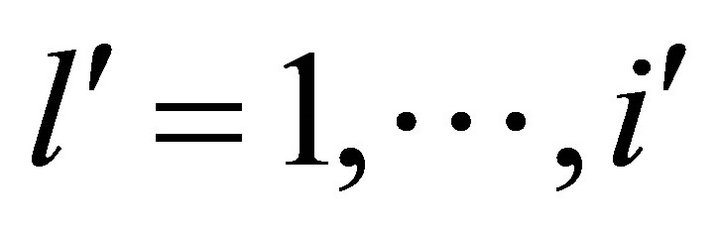 .
.
Theorem 2.2. For any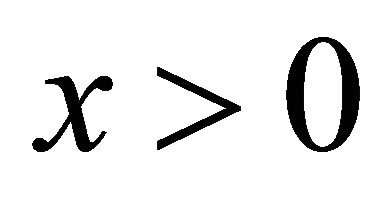 , we have
, we have
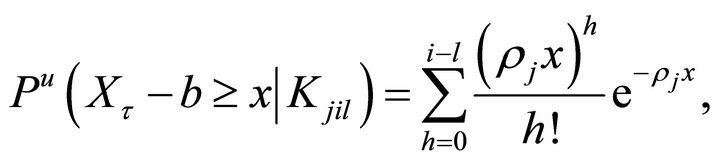 (2.1)
(2.1)
 (2.2)
(2.2)
Furthermore, conditional on 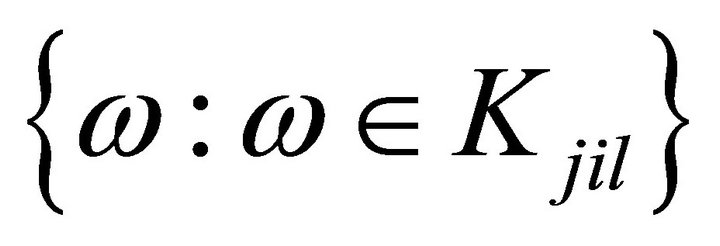
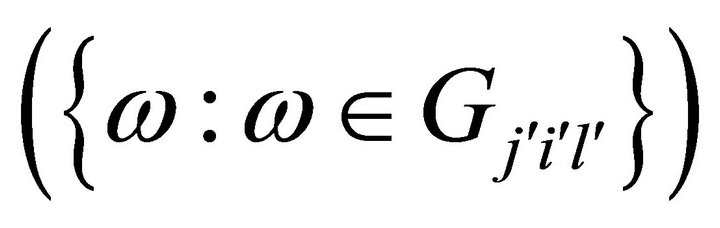 , the stopping time
, the stopping time  is independent of the overshoot
is independent of the overshoot 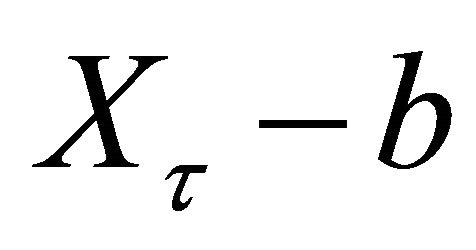 (the undershoot
(the undershoot ). More precisely, for any
). More precisely, for any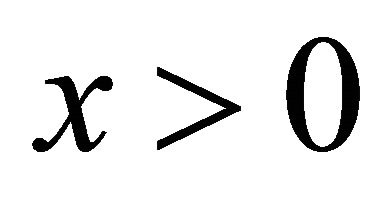 , we have
, we have
 (2.3)
(2.3)
 (2.4)
(2.4)
Proof. Firstly, we prove (2.1) and (2.3). It suffices to show
 (2.5)
(2.5)
since (2.1) can be obtained by letting  in (2.5) and then dividing both sides of the resulting equation by
in (2.5) and then dividing both sides of the resulting equation by . It is known that an Erlang(n) random variable can be expressed as an independent sum of
. It is known that an Erlang(n) random variable can be expressed as an independent sum of  exponential random variables with same parameters. Let
exponential random variables with same parameters. Let  the
the  independent exponentially distributed random variables with parameter
independent exponentially distributed random variables with parameter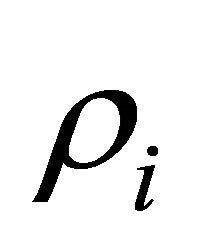 . Denote by
. Denote by  the arrival times of the Poisson process
the arrival times of the Poisson process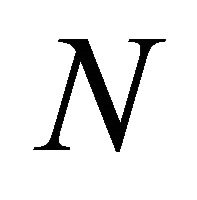 , and let
, and let 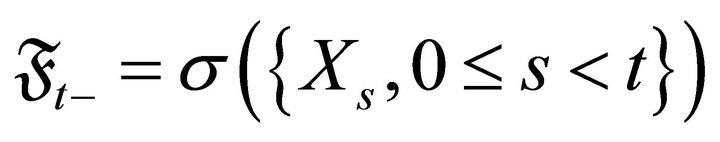 be the field generated by process
be the field generated by process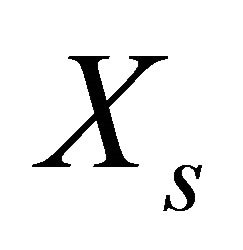 ,
, . It follows that
. It follows that
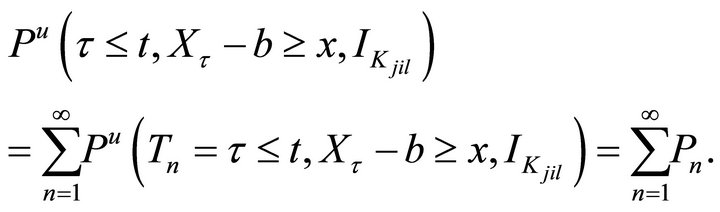
With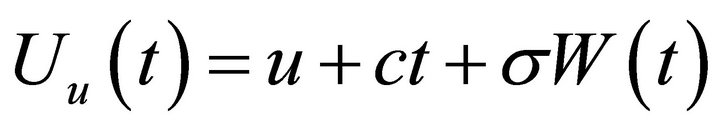 , we have
, we have

Thus we have
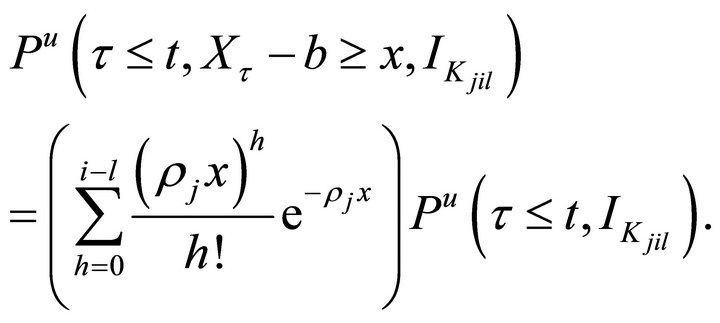
(2.2) and (2.4) can be obtained similarly. This completes the proof.
The following results are immediate consequences of Theorem 2.2.
Corollary 2.3. For ,
,  ,
,  ,
,  ,
,  ,
,  , we have
, we have


Corollary 2.4. For any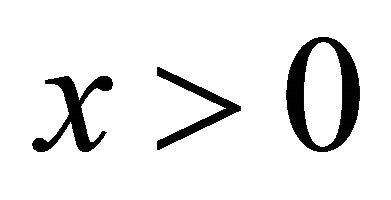 , we have
, we have

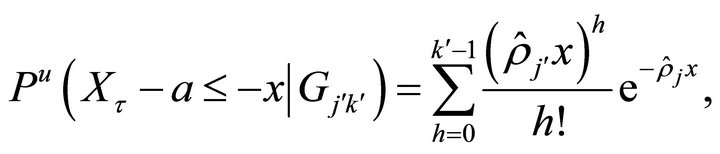


where
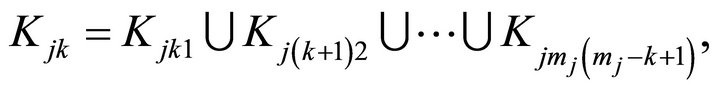
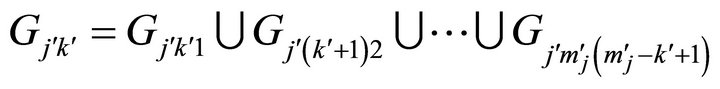
for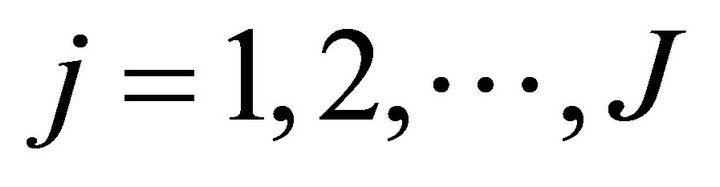 ,
, 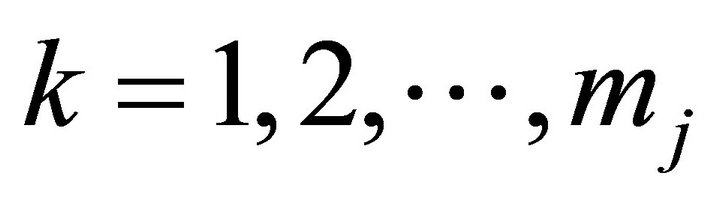 ,
, 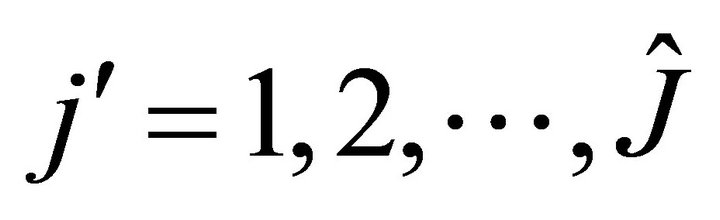 ,
, 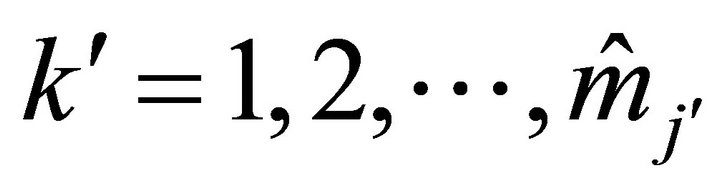 .
.
Corollary 2.5. For ,
,  ,
,  ,
, 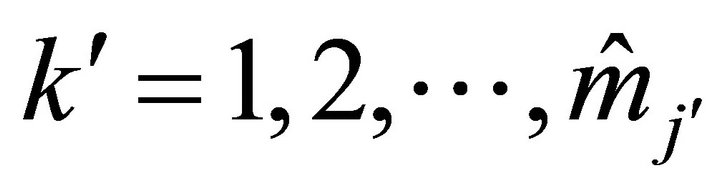 , we have
, we have
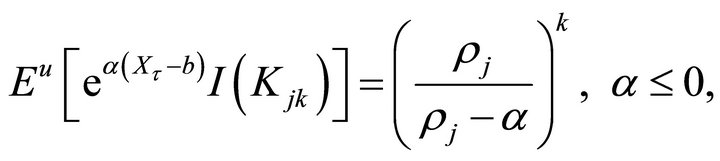

Remark 2.6. When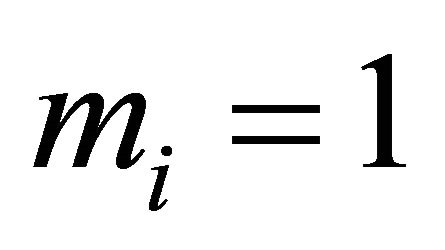 ,
,  , (2.1) and (2.3) reduce to Equations (8) and (9) of Cai [3], respectively.
, (2.1) and (2.3) reduce to Equations (8) and (9) of Cai [3], respectively.
3. Main Results
In this section, we study the distribution of the first exit problem to two barriers. We first define three vectors:
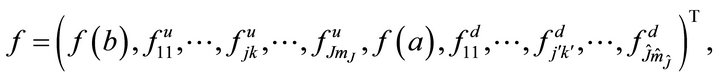

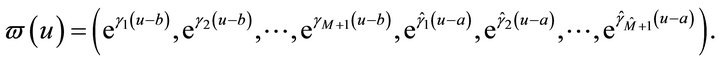
where
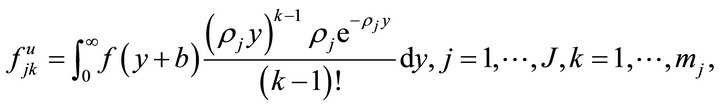
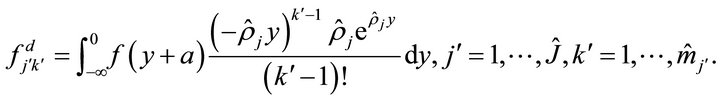
Let

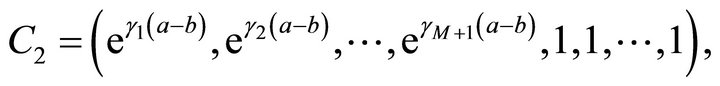
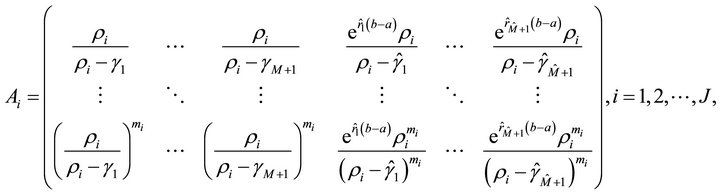

Define a matrix 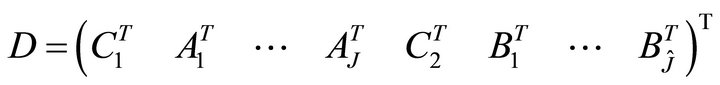 .
.
Theorem 3.1. Consider any nonnegative measurable function  such that
such that 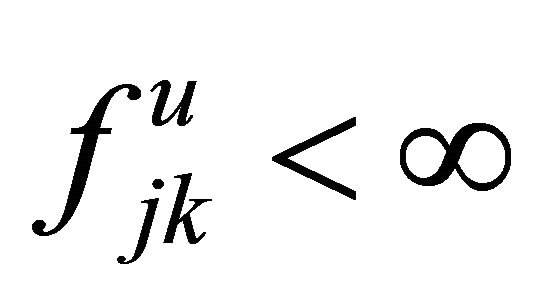 and
and 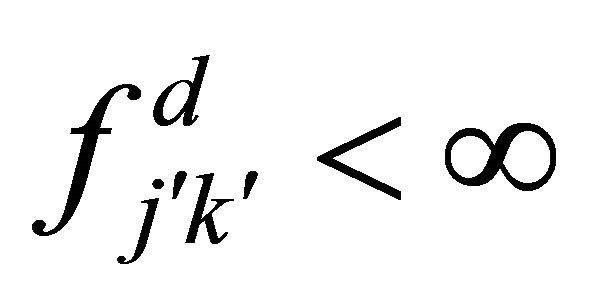 for
for ,
, 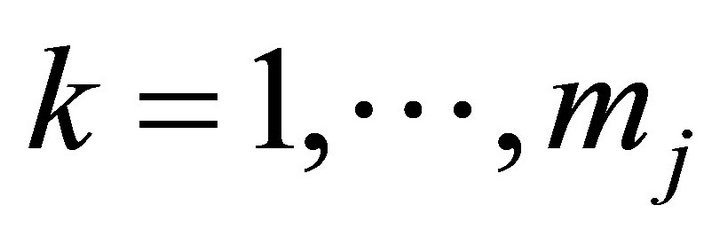 ,
, 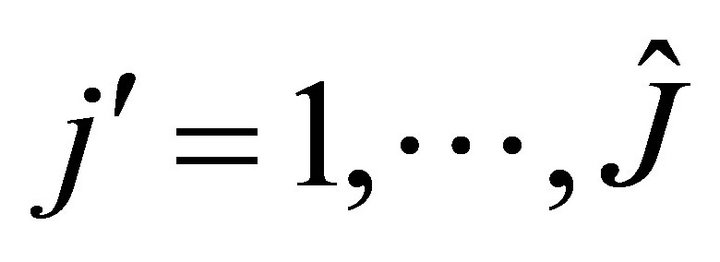 ,
, . For any
. For any 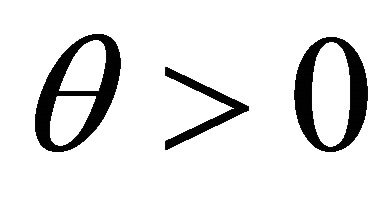 and
and , we have
, we have
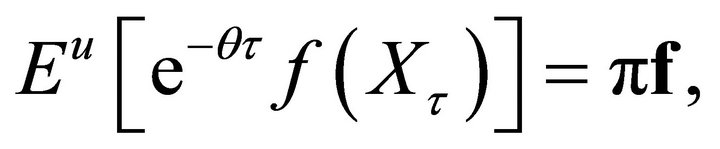 (3.1)
(3.1)
where  satisfies
satisfies
 (3.2)
(3.2)
Moreover, when 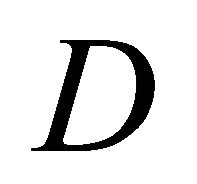 is a non-singular matrix,
is a non-singular matrix,  is the unique solution of (3.2), i.e.,
is the unique solution of (3.2), i.e.,
 (3.3)
(3.3)
Proof. By the law of total probability, we have

It follows from Corollary 2.4, for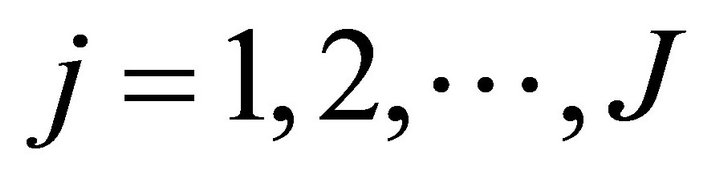 ,
, 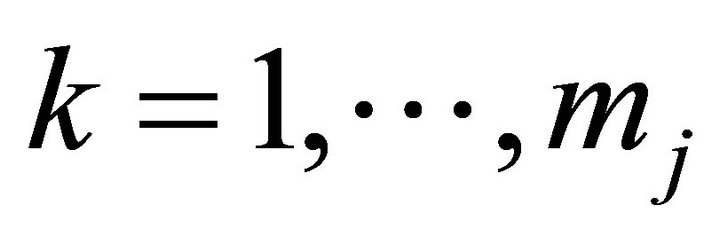 ,
, 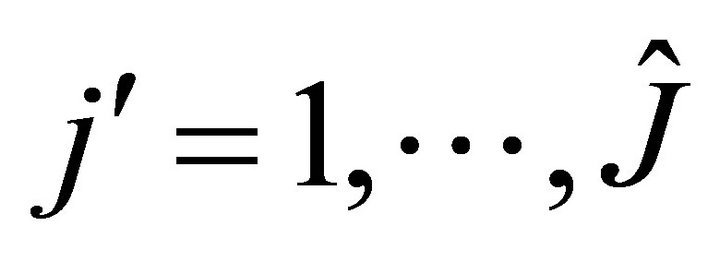 ,
, 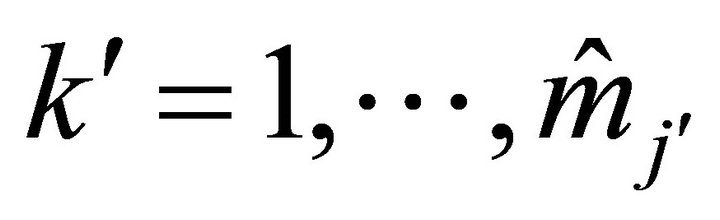 , we have
, we have

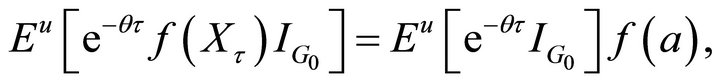

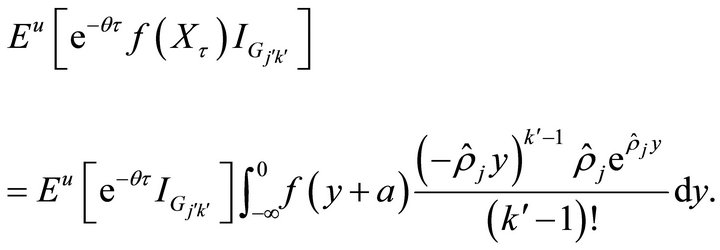
Combining these equations, we get
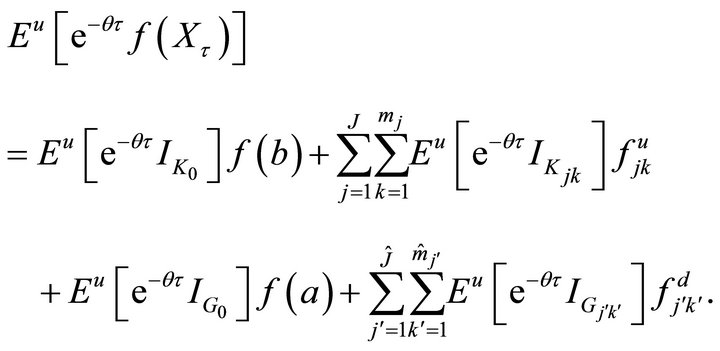
The expressions for ,
, 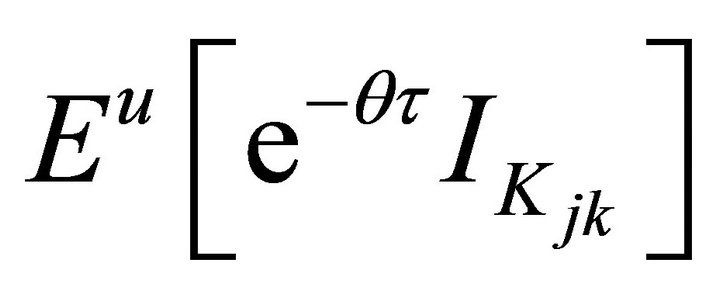 ,
, 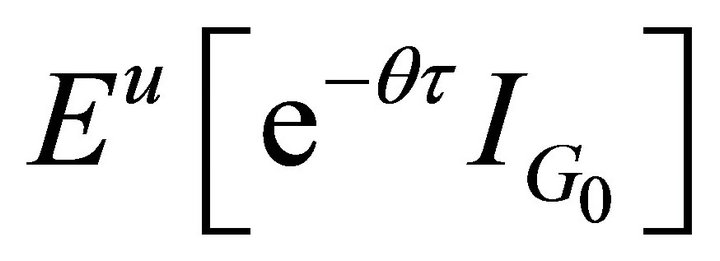 and
and  can be determined as follows. Let
can be determined as follows. Let  denote the set of functions
denote the set of functions 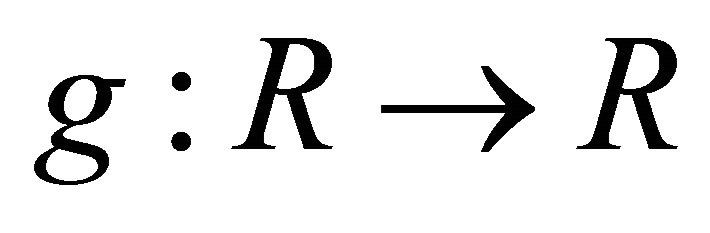
such that 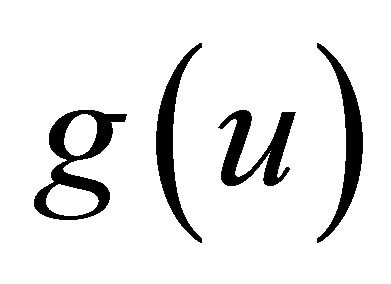 is twice continuously differentiable and bounded for
is twice continuously differentiable and bounded for  with
with 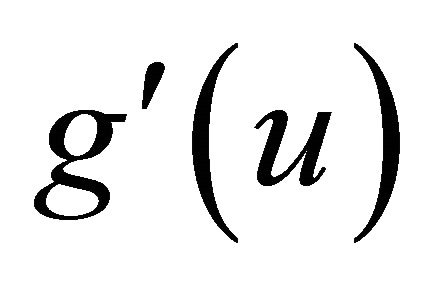 and
and 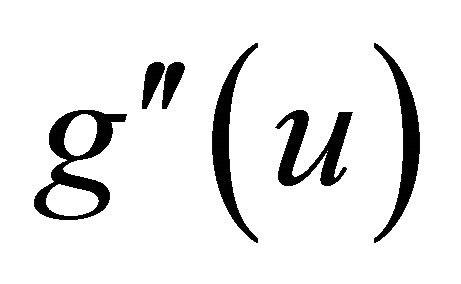 bounded for
bounded for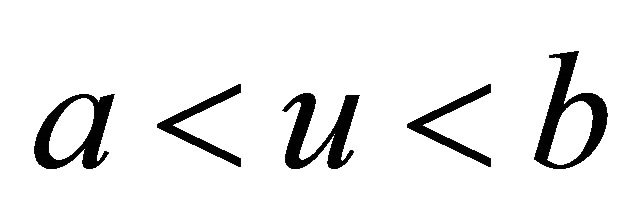 . By applying Itô formula to the process
. By applying Itô formula to the process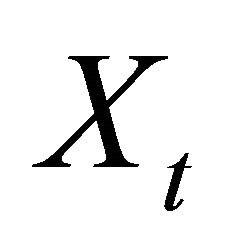 , we have that for
, we have that for 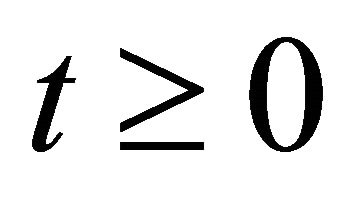 and
and ,
,

where 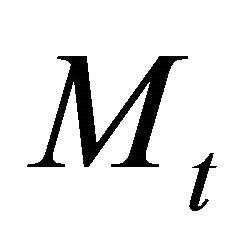 is a martingale with
is a martingale with . Note that we have
. Note that we have  as
as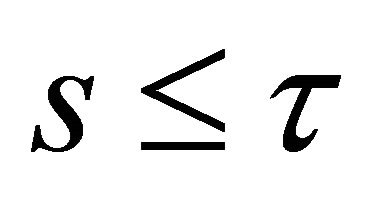 .
.
For any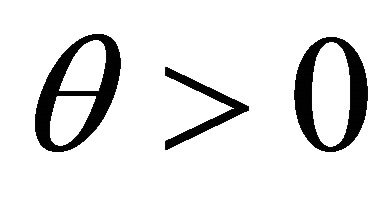 , we can easily obtain from the above equation that
, we can easily obtain from the above equation that

where the last term of the above equation is a mean-0 martingale. This implies that
 (3.4)
(3.4)
By simple calculation, the function 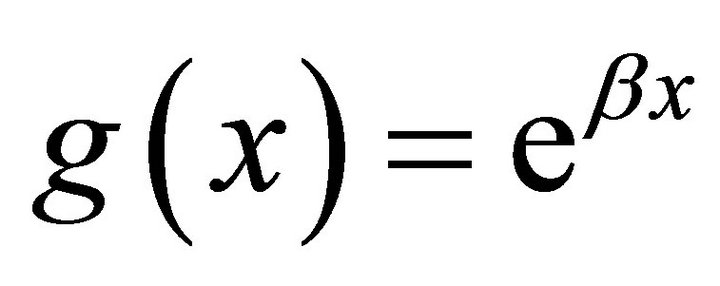 with
with 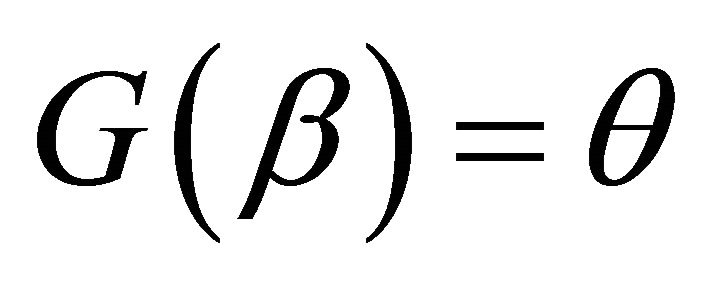 and
and  satisfies
satisfies 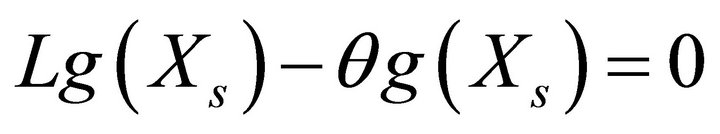 for
for . It follows from (3.4) that the process
. It follows from (3.4) that the process
 is a martingale. Then
is a martingale. Then
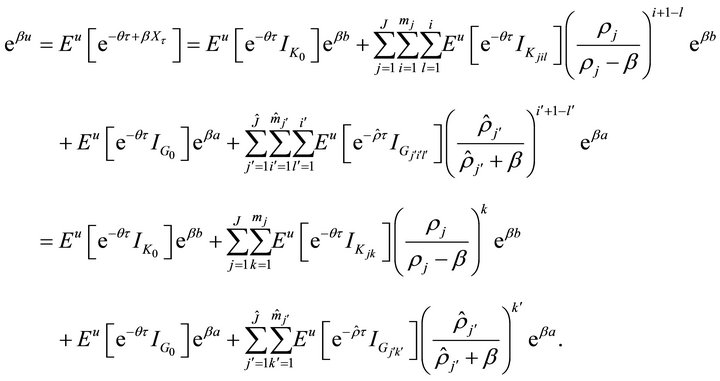 (3.5)
(3.5)
Setting  for
for  and
and 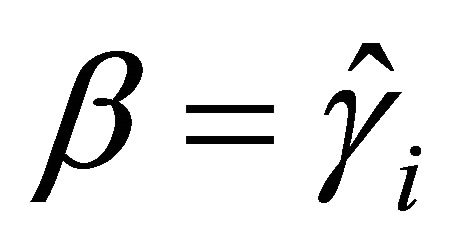 for
for 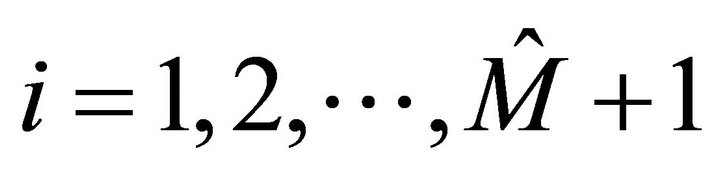 in (3.5), we have the following linear equations:
in (3.5), we have the following linear equations:
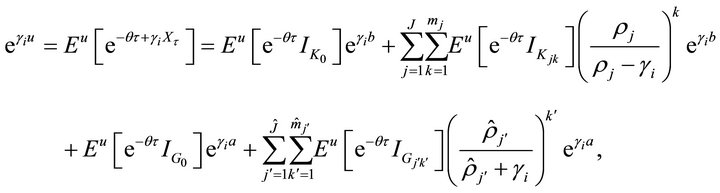
and
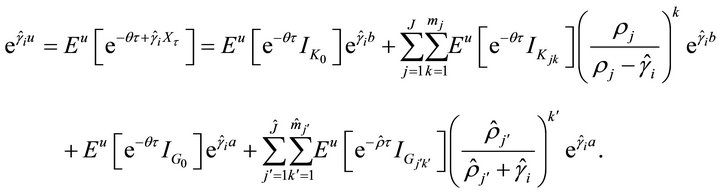
Then the vector  satisfies
satisfies 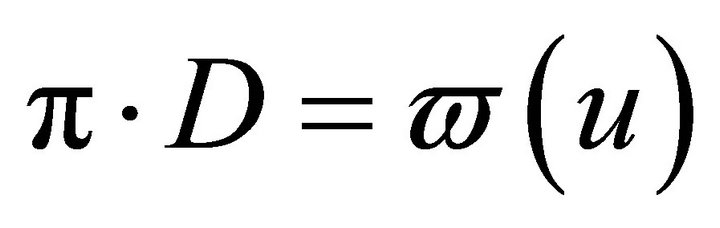 and we have (3.1). If
and we have (3.1). If  is non-singular, we have
is non-singular, we have  . This completes the proof.
. This completes the proof.
Corollary 3.2. For any
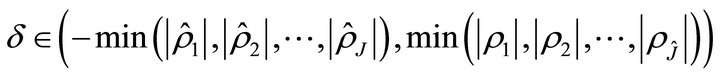 , we have
, we have
 (3.6)
(3.6)
where
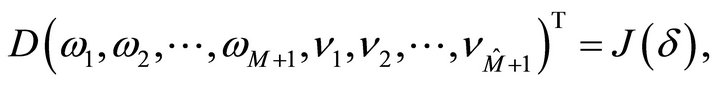
and
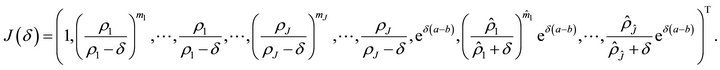
Remark 3.3. When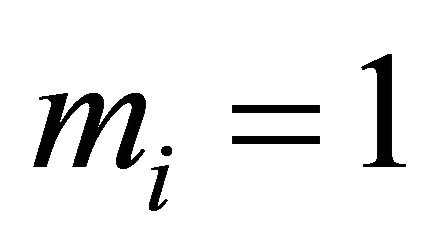 ,
, 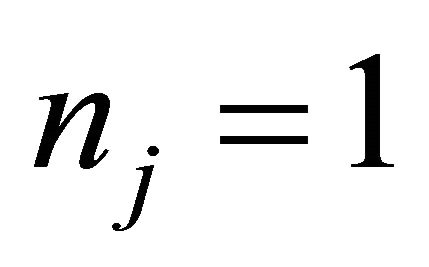 , (3.1) and (3.6) reduce to equation (6) and (15) of [4], respectively.
, (3.1) and (3.6) reduce to equation (6) and (15) of [4], respectively.
From Theorem 3.1, choosing 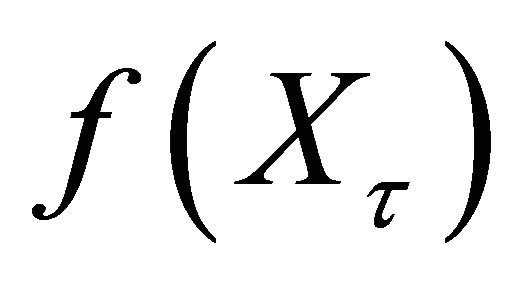 to be
to be ,
,
 ,
, 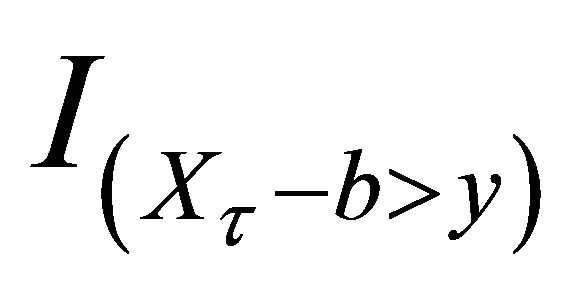 ,
, 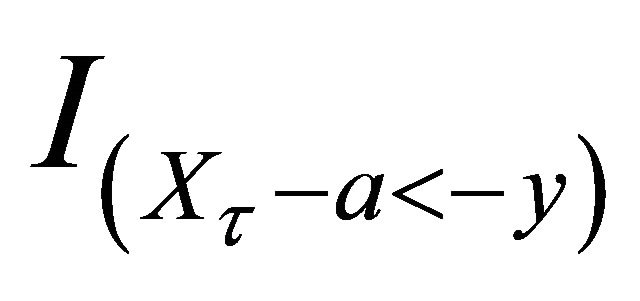 ,
, 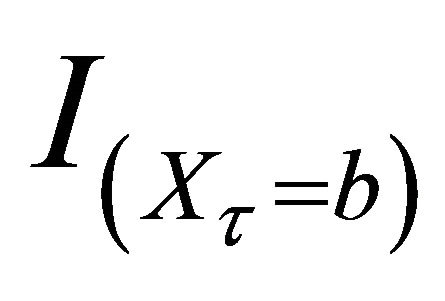 ,
, 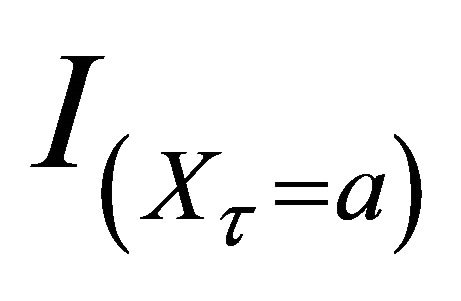 and
and 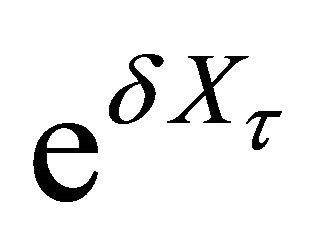 respectively, we can obtain the following corollaries.
respectively, we can obtain the following corollaries.
Corollary 3.4. 1) For any , we have
, we have
 (3.7)
(3.7)
where

is determined by the linear system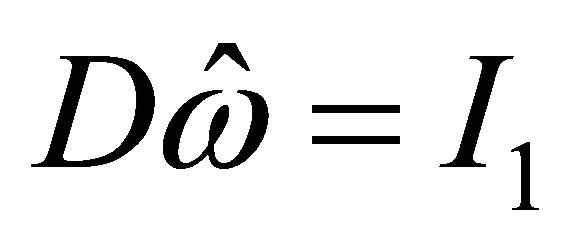 . Here
. Here

2) For any , we have
, we have
 (3.8)
(3.8)
where

is determined by the linear system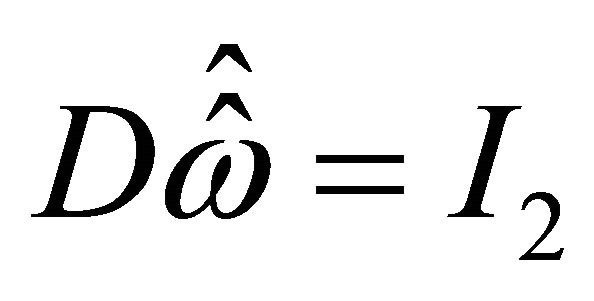 . Here
. Here
Corollary 3.5. 1) For  and any
and any ,
,  , we have
, we have
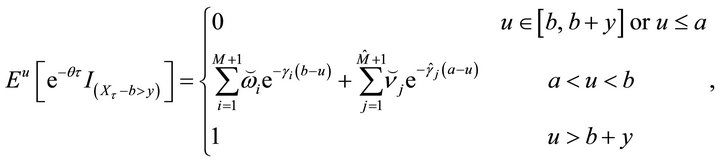 (3.9)
(3.9)
where

is determined by the linear system . Here
. Here
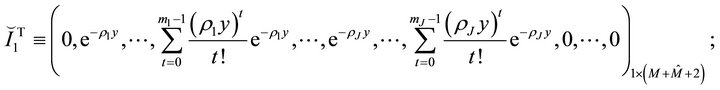
2) For 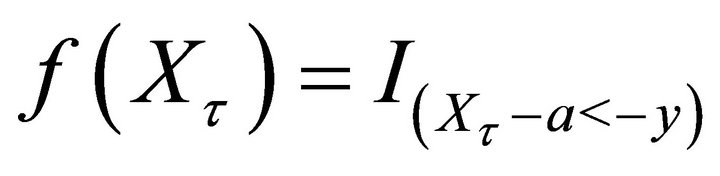 and any
and any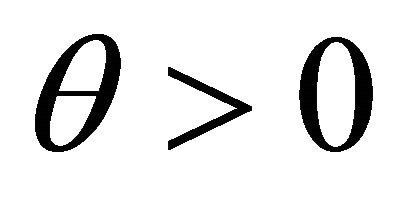 ,
, 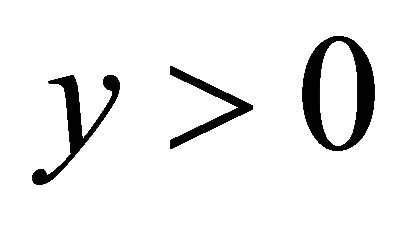 , we have
, we have
 (3.10)
(3.10)
where

is determined by the linear system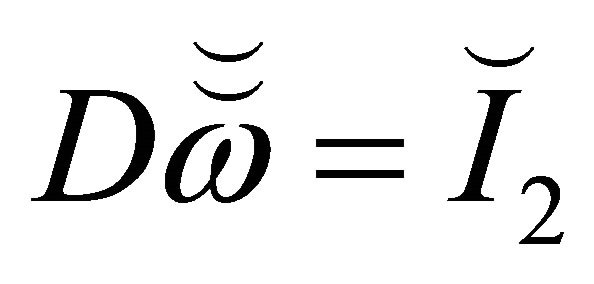 . Here
. Here
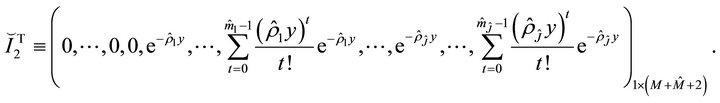
Note that the difference of 
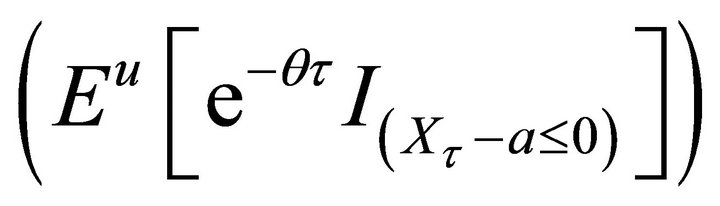 and
and 
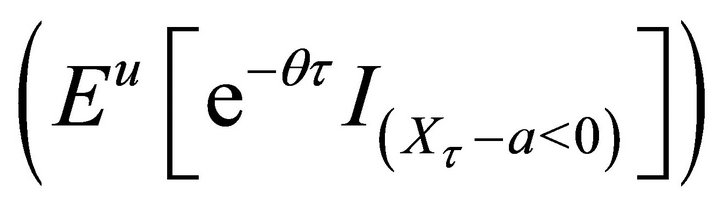 is exactly
is exactly 
 . Thus we obtain the following results.
. Thus we obtain the following results.
Corollary 3.6. 1) For , and for any
, and for any , we have
, we have
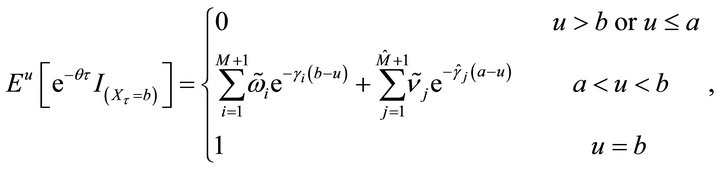 (3.11)
(3.11)
where
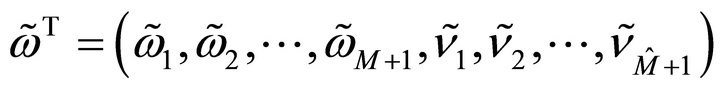
is determined by the linear system . Here
. Here

2) For  and any
and any ,
,  , we have
, we have
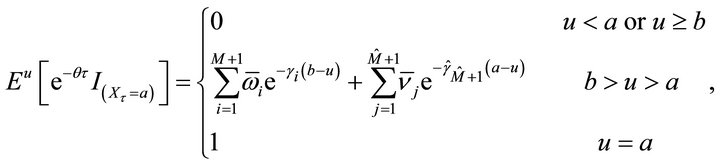 (3.12)
(3.12)
where
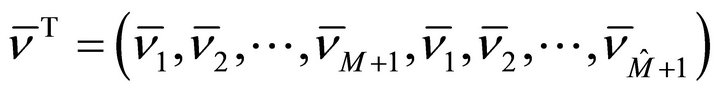
is determined by the linear system . Here
. Here
To end the paper, we give an example.
Example 3.7. When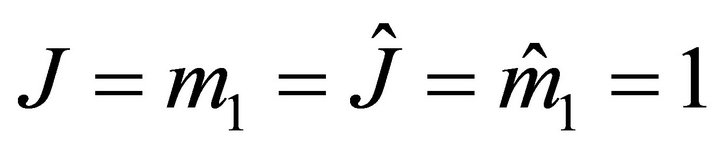 ,
,
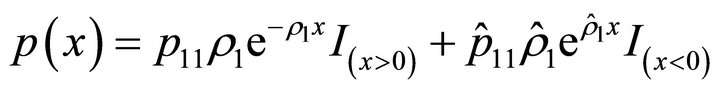 and
and
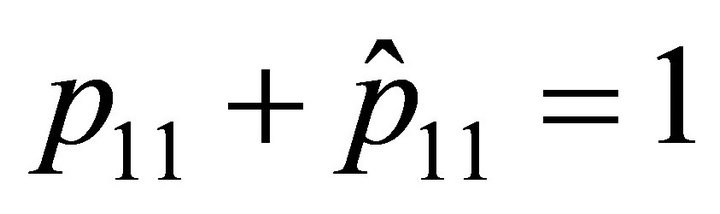 , the equation
, the equation  has
has  real roots:
real roots: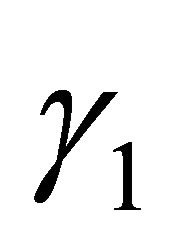 ,
, 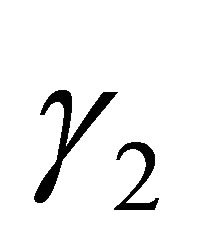 ,
, 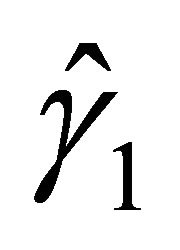 and
and 
 . Let
. Let

Denote 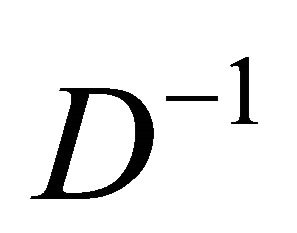 by
by
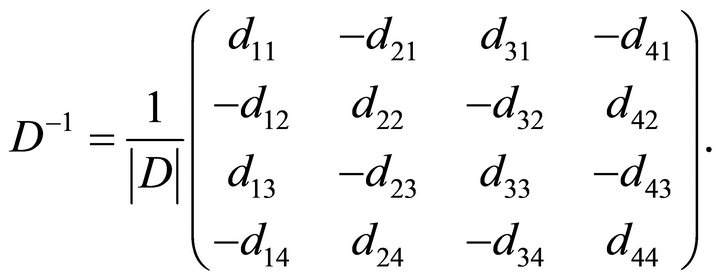
Then we have
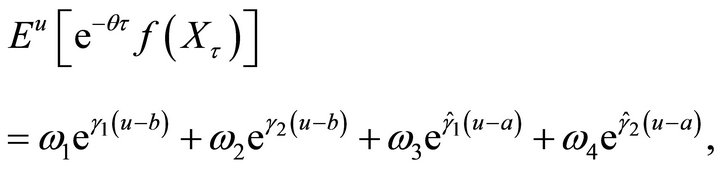
where
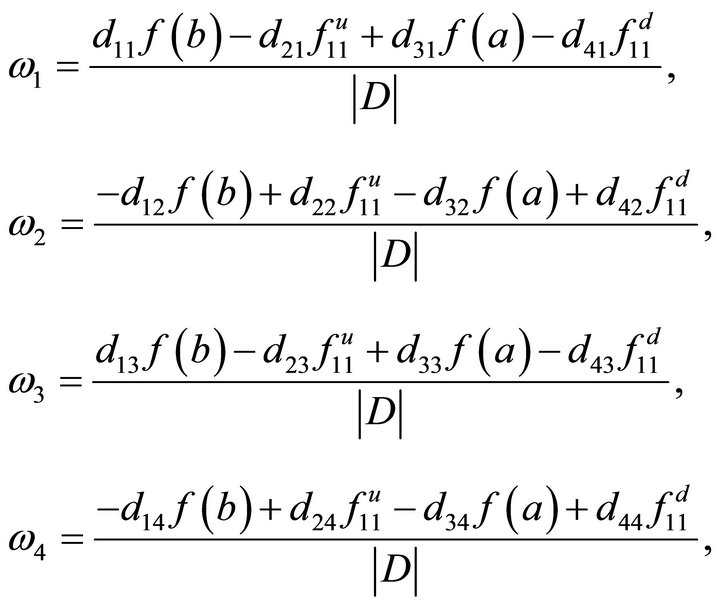


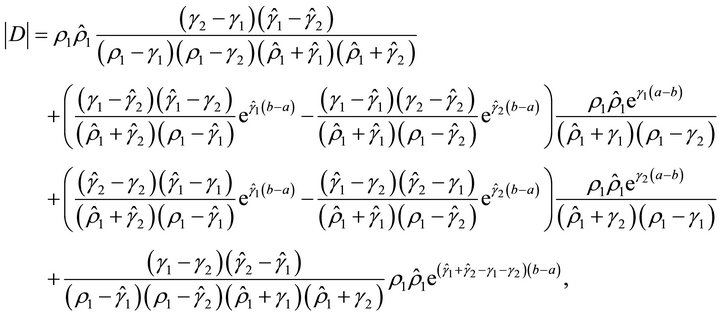

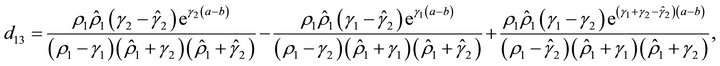


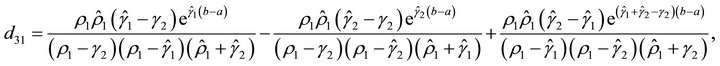
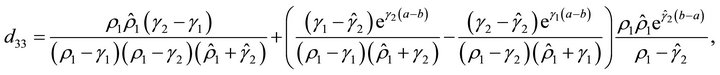
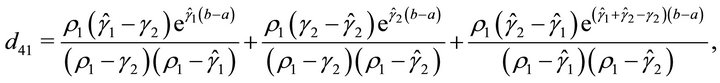
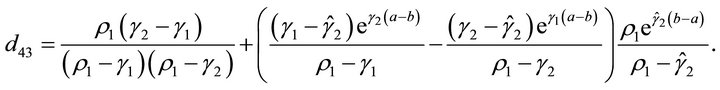
We define 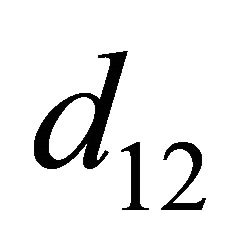 (
(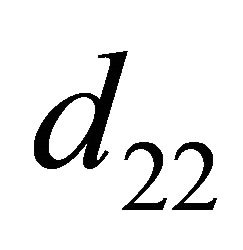 ,
, 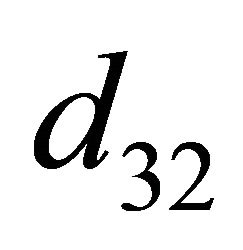 ,
,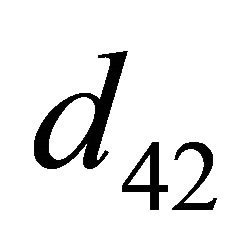 ) and
) and  (
( ,
,  ,
, ) as follows: let
) as follows: let  (
(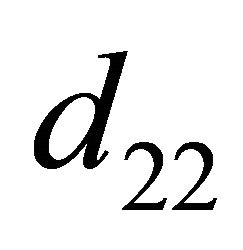 ,
, 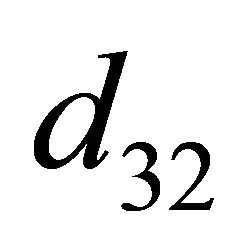 ,
,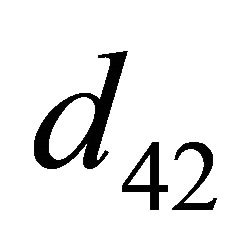 ) be obtained from
) be obtained from  (
(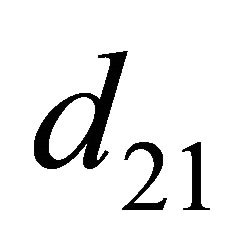 ,
, 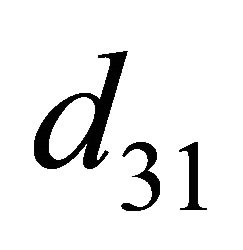 ,
, ) by changing
) by changing  to
to 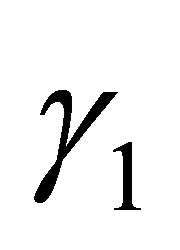 in
in  (
(
 ,
, ); let
); let  (
(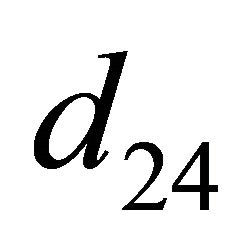 ,
,  ,
, ) be obtained from
) be obtained from  (
(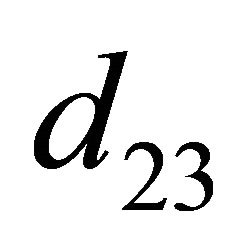 ,
,  ,
, ) by changing
) by changing 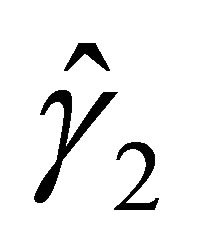 to
to 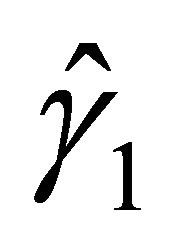 in
in  (
(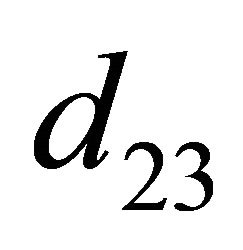 ,
,  ,
, ).
).
• If , then we have
, then we have
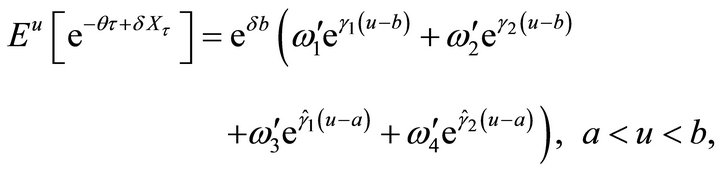
where
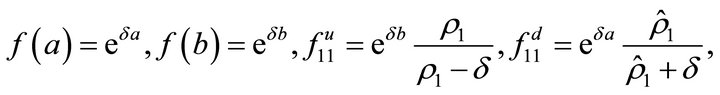
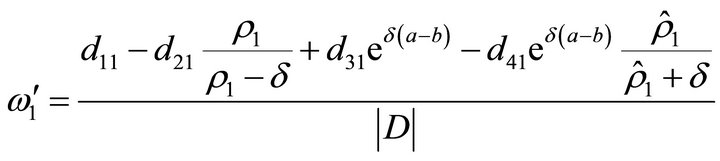
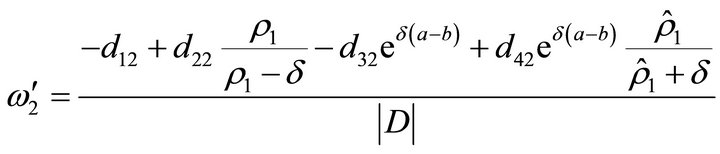
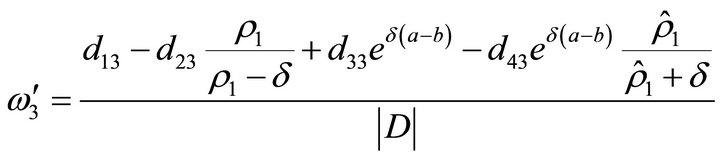
• 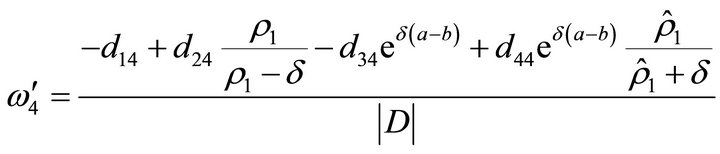
• If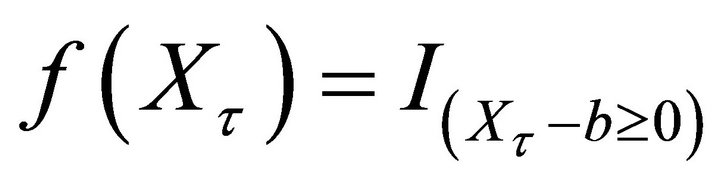 , then we have
, then we have
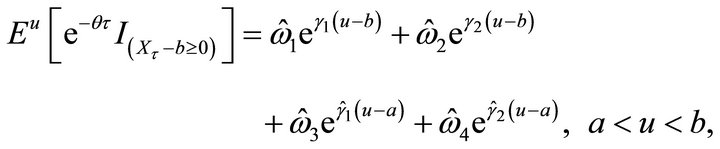
where
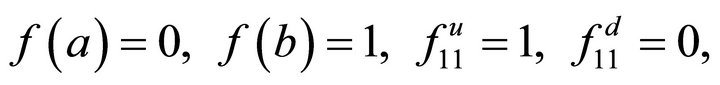
• 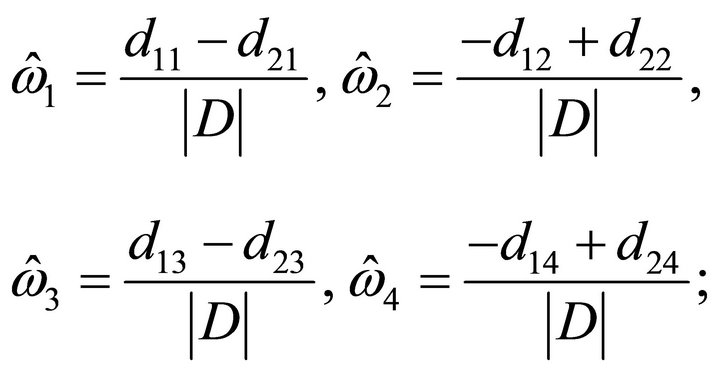
• If , then we have
, then we have

where
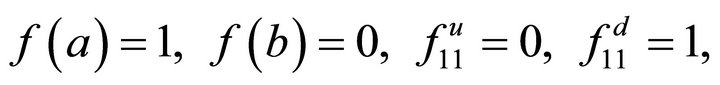
• 
• If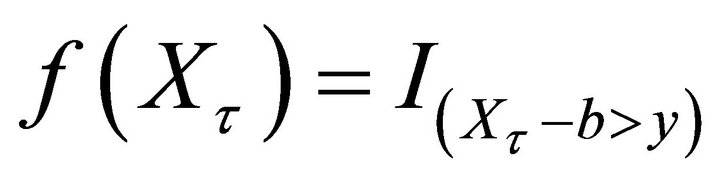 ,
,  , then we have
, then we have


• 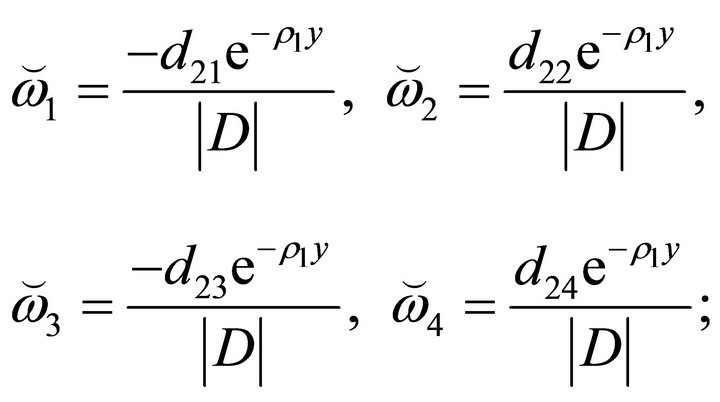
• If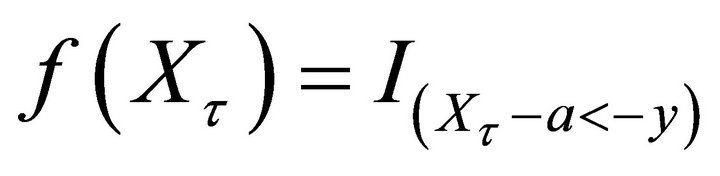 ,
, 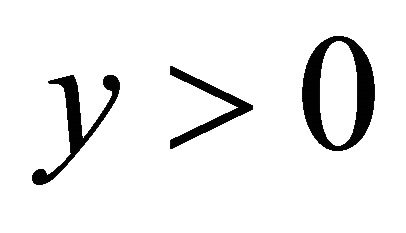 , then we have
, then we have

where

• 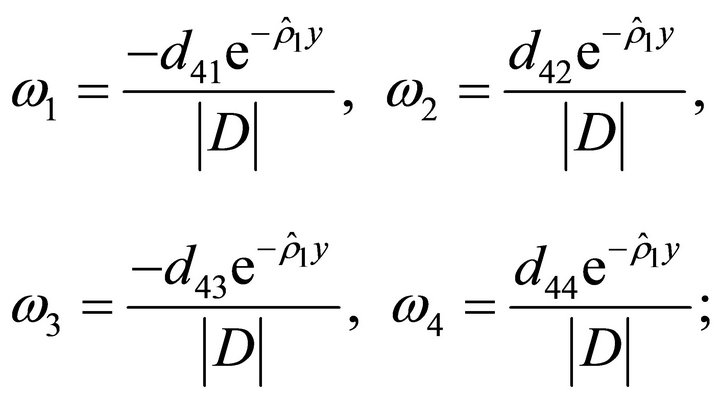
• If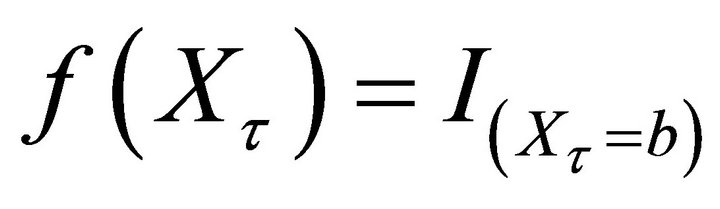 , then we have
, then we have
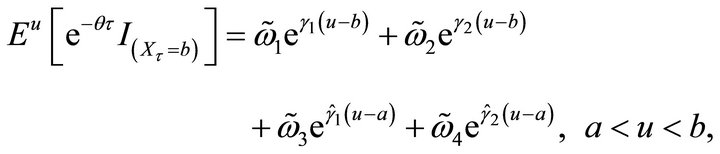
where
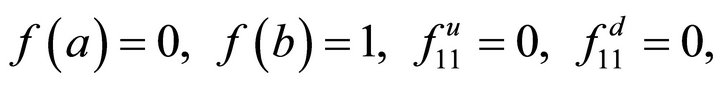
• 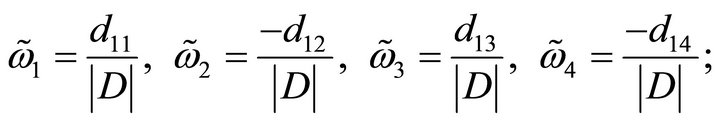
• If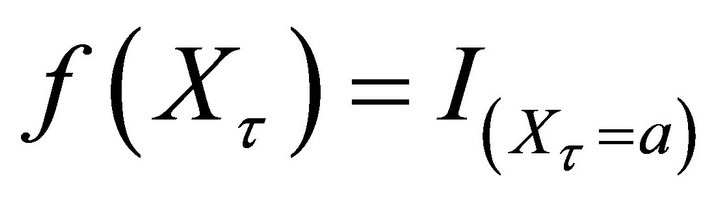 , then we have
, then we have
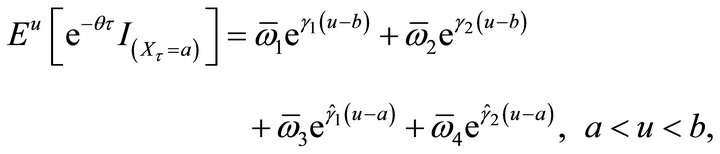
where


When , we have
, we have

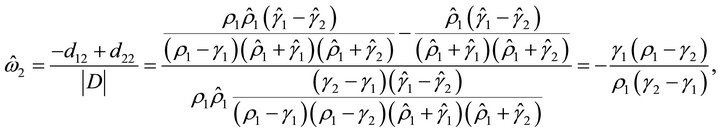



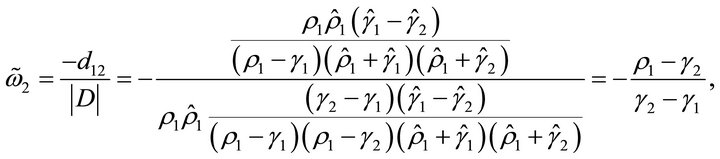
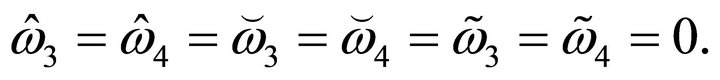
Therefore, we have

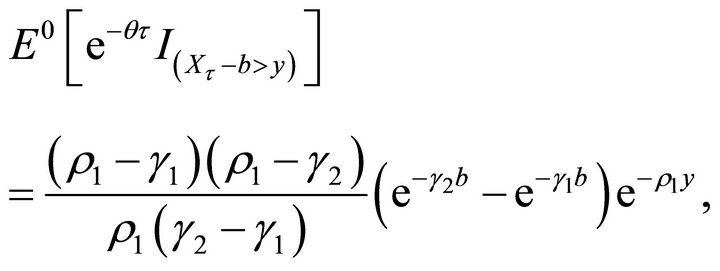

These results are all consistent with that of Theorem 3.1 of Kou and Wang [2] for the one-sided exit problem of the doubly exponential jump diffusion process.
REFERENCES
- D. Perry and W. Stadje, “Risk Analysis for a Stochastic Cash Management Model with Two Types of Customers,” Insurance: Mathematics and Economics, Vol. 26, No. 1, 2000, pp. 25-36. doi:10.1016/S0167-6687(99)00037-2
- S. G. Kou and H. Wang, “First Passage Times of a Jump Diffusion Process,” Advances in Applied Probability, Vol. 35, No. 2, 2003, pp. 504-531. doi:10.1239/aap/1051201658
- N. Cai, “On First Passage Times of a Hyper-Exponential Jump Diffusion Process,” Operations Research Letters, Vol. 37, No. 2, 2009, pp. 127-134. doi:10.1016/j.orl.2009.01.002
- N. Cai, N. Chen and X. W. Wan, “Pricing Double-Barrier Options under a Flexible Jump Diffusion Model,” Operations Research Letters, Vol. 37, No. 3, 2009, pp. 163-167. doi:10.1016/j.orl.2009.02.006
- T. Kadankova and N. Veraverbeke, “On Several TwoBondary Problems for a Particular Class of Lévy Processes,” Journal of Theoretical Probability, Vol. 20, No. 4, 2007, pp. 1073-1085. doi:10.1007/s10959-007-0088-8
- S. Fourati, “Explicit Solutions of the Exit Problem for a Class of Lévy Processes; Applications to the Pricing of Double-Barrier Options,” Stochastic Processes and their Applications, Vol. 122, No. 3, 2012, pp. 1034-1067. doi:10.1016/j.spa.2011.09.008
- M. Jacobsen, “The Time to Ruin for a Class of Markov Additive Risk Process with Two-Sided Jumps,” Advances in Applied Probability, Vol. 37, No. 4, 2005, pp. 963-992. doi:10.1239/aap/1134587749
- D. Perry, W. Stadje and S. Zacks, “Contributions to the Theory of First-Exit Times of Some Compound Processes in Queueing Theory,” Queueing Systems, Vol. 33, No. 4, 1999, pp. 369-379. doi:10.1023/A:1019140616021
- N. Cai and S. G. Kou, “Option Pricing under a Mixed-Exponential Jump Diffusion Model,” Management Science, Vol. 57, No. 11, 2011, pp. 2067-2081. doi:10.1287/mnsc.1110.1393
- A. L. Lewis and E. Mordecki, “Wiener-Hopf Factorization for Lévy Processes Having Positive Jumps with Rational Transforms,” Journal of Applied Probability, Vol. 45, No. 1, 2008, pp. 118-134. doi:10.1239/jap/1208358956
- A. Kuznetsov, “On the Distribution of Exponential Functionals for Lévy Processes with Jumps of Rational Transform,” Stochastic Processes and their Applications, Vol. 122, No. 2, 2012, pp. 654-663. doi:10.1016/j.spa.2011.09.007
NOTES
*This work was supported by the National Natural Science Foundation of China (No. 11171179) and Natural Science Foundation of Shandong Province (No. ZR2010AQ015).
#Corresponding author.

