Applied Mathematics
Vol.4 No.2(2013), Article ID:28194,5 pages DOI:10.4236/am.2013.42046
Fractional Order for Food Gums: Modeling and Simulation
Department of Basic Sciences, University of São Paulo, São Paulo, Brazil
Email: sergiodavid@usp.br, aline.katayama@usp.br
Received December 10, 2012; revised January 4, 2013; accepted January 12, 2013
Keywords: Fractional Calculus; Mathematical Model; Food Gums; Viscoelasticity
ABSTRACT
Fractional order calculus can represent systems with high-order dynamics and complex nonlinear phenomena using few coefficients, since the arbitrary order of the derivatives provides an additional degree of freedom to fit a specific behavior. Numerous mathematicians have contributed to the history of fractional calculus by attempting to solve a fundamental problem to the best of their understanding. Each researcher sought a definition and therefore different approaches, which has led to various definitions of differentiation and anti-differentiation of non-integer orders that are proven equivalent. Although all these definitions may be equivalent, from one specific standpoint, i.e., for a specific application, some definitions seem more attractive. Furthermore, it is well known that food gums are complex carbohydrates that can suit for a wide variety of functions in the context of food engineering. The viscoelastic behavior of food gums is crucial for these applications and formulations of new or improved food products. Small progress has been made to understand the viscoelastic behavior of food gums and there are few studies in the literature about these models. In this paper, we applied the Riemann-Liouville approach and the Fourier transform in order to obtain numerical simulations results of a fractional derivative model based on previous literature that to make a quantitative description of the viscoelastic properties behavior for a food gum. The results reveal that the fractional model shows good simulation capability and can be an attractive means for predicting and to elucidate the dynamic viscoelastic behavior of food gums.
1. Introduction
It is known that, historically, fractional calculus (FC) is the subarea of Science that investigates and applies the concepts that involve derivatives of non-integer order. However, until recently, applications involving derivatives and integrals of non-integer order did not advance at the same pace as calculus of integer order. Nevertheless, in the last few years, scientific and technological advances have sparked renewed interest in this field of research. Many research centers, particularly in Europe and the United States, have worked with FC applications in, for example, physics, chemistry, wave diffusion and propagation, biology, electromagnetism, image processing, and others.
With regard to its applications in food engineering, this area can be considered to be practically untouched by this mathematical tool. That, allied to the fact that food gums are complex carbohydrates with a variety of functions in the context of food engineering, has motivated this project. Food gums are useful in the production of many foods, e.g., in the design and modification of the texture of the product. The viscoelastic behavior of food gums is crucial for applications that involve new or improved formulations of food products. In essence, the models thus developed can considered to comprise two parts: one that involves the viscous behavior and another that involves the elastic behavior. Few studies about these models are available in the literature, and therefore the goal of this work is to use fractional calculus as a tool to model and simulate the viscoelastic behavior of food gums.
This paper is organized as follows: after this introductory section, section two offers a brief literature review about the food gums and fractional calculus—origins and approaches. Section three describes the mathematical model used here, while section four presents the main numerical simulations results and our findings, and lastly, section five presents our discussion and conclusions.
2. Literature Review of Support
2.1. Food Gums
Gums present important properties for the food industry, such as thickeners of aqueous solutions, dispersing agents, emulsion and suspension stabilizers, stabilizers of room temperature, rheological and pseudoplastic properties, and compatibilizers of food ingredients [1].
Gums are complex carbohydrates with various rheological properties that result in viscoelastic behavior. According to Luvielmo et al. [1], xanthan gum solutions, for example, are non-Newtonian fluids that are highly pseudo-plastic, i.e., their viscosity decreases as the strain rate of the fluid increases. However, according to Salah and Besbes [2], in 1978, Whitcomb and Macosko [3] investigated the rheology of aqueous solutions of xanthan gum over a wide range of shear rates and found that the solution behaves like a Newtonian fluid when sufficiently diluted and at low shear rates. Studies conducted by Lopes da Silva et al. [4] and Kobayashi and Nakahama [5] presented positive results that increased the understanding of the viscoelastic behavior of food gums. Understanding this behavior by means of theoretical mechanisms can provide guidelines to relate the behavior with the composition and structure. However, much remains to be investigated through modeling and simulation of such gums in order to obtain information to enable the right choice of this food ingredient. Moreover, such investigations may lead to the discovery of solutions to further enhance the attractiveness of food products that use such gums.
2.2. Fractional Calculus
The theory of fractional calculus dates back to the birth of the theory of differential calculus, but its inherent complexity delayed the application of its associated concepts [6,7]. In fact, fractional calculus is a natural extension of classical mathematics. Since the inception of the theory of differential and integral calculus, mathematiccians such as Euler and Liouville developed their ideas about the calculation of non-integer order derivatives and integrals. Perhaps the subject would be more aptly called “integration and differentiation of arbitrary order”.
The best-known definitions and gained more popularity in the scientific definitions were the Riemann-Liouville and Grünwald-Letnikov [6]. Caputo [8] reformulated the definition of fractional derivative given by the Riemann-Liouville initial conditions so as to incorporate the integer order to solve differential equations of fractional order.
Many of the theories applied to the study of (FC) has been developed in the second half of the nineteenth century and, therefore, only in the twentieth century is that there have been some applications of this theory in science and engineering areas.
Within this context, this topic can be considered “new”, since there are about thirty years held the first conference on the subject and the first book entirely devoted to this subject was published in 1974 by K. B. Oldham and J. Spanier [6]. Today, the list of texts and papers that refer to concepts and applications of (FC) in several areas, for instance, control theory, diffusion processes, electricity, modal analysis, among others, has already reached a high number [6-12].
2.3. Fractional Calculus—Approaches
Numerous mathematicians have contributed to the history of fractional calculus by attempting to solve a fundamental problem to the best of their understanding.
Each researcher sought a definition and therefore different approaches, which has led to various definitions of differentiation and anti-differentiation of non-integer orders that are provenly equivalent [6,9].
Although Leibniz (1695), Euler (1730) and Laplace (1812) had wondered about the non-integer order derivatives, a first discussion about fractional order calculus has been described by Lacroix in 1819 [9].
One can found in David et al. [7] that organized and presented these and others settings most recurrent and important approaches about FC such as listed in Table 1.
Although all these definitions may be equivalent, from one specific standpoint, i.e., for a specific application, some definitions seem more attractive. In the Section 3, one can note the mathematical model involving the viscoelastic behavior of food gums in the context of fractional order calculus.
3. Mathematical Model
For Newtonian viscous fluids, then following relationship is applicable:
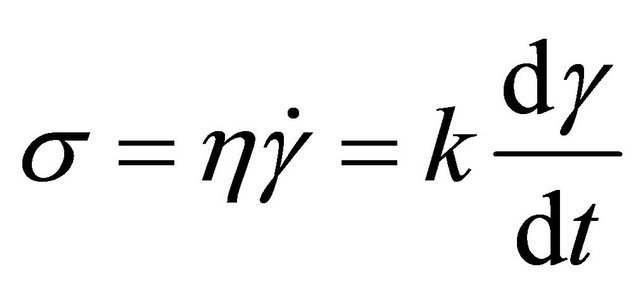 (1)
(1)
where ![]() is the shears stress,
is the shears stress, 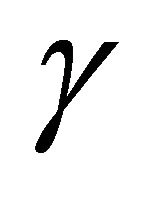 is the shear strain,
is the shear strain, 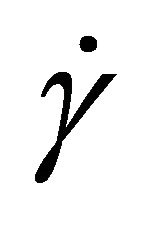 is the shear strain rate ,
is the shear strain rate ,  is the viscosity and
is the viscosity and 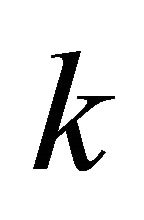 is a
is a
Table 1. Fractional derivatives—different approaches.

constant. It is also well known that for elastic bodies (Hookean):
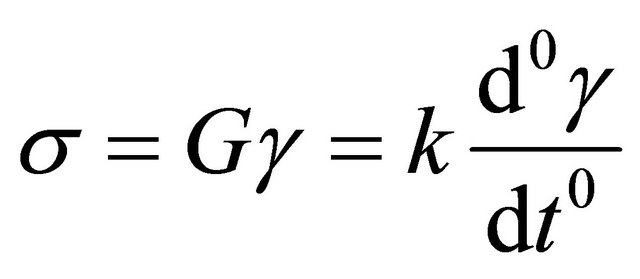 (2)
(2)
where ![]() is the shears stress,
is the shears stress,  is the shear strain, G is the elastic modulus and
is the shear strain, G is the elastic modulus and 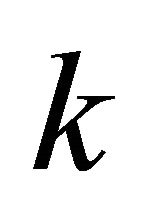 is a constant.
is a constant.
For a material that is neither a Hookean solid nor a Newtonian fluid, Ma and Barbosa-Cánovas [11] proposed the following relationship:
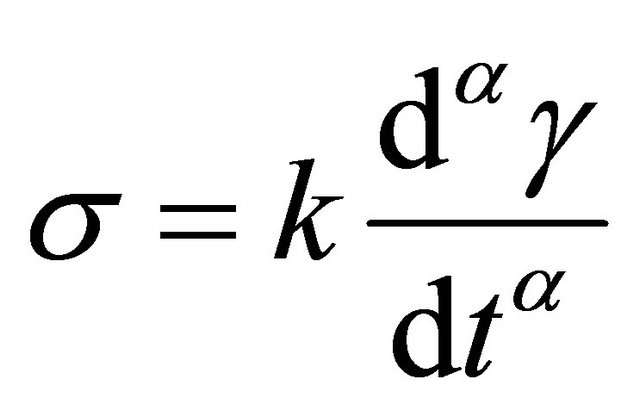 (3)
(3)
where k is a constant, 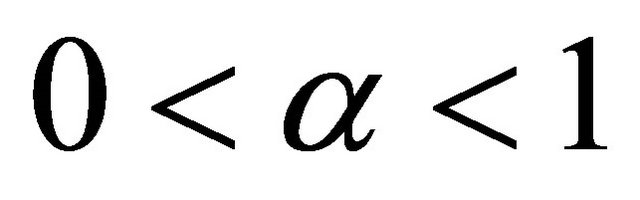 ,
, ![]() is the shear stress and
is the shear stress and  is the shear strain.
is the shear strain.
Based on the last equation that describes a linear viscoelastic behavior and by applying the Boltzmann superposition principle using a fractional derivative operator, the Equation (3) has the following form:
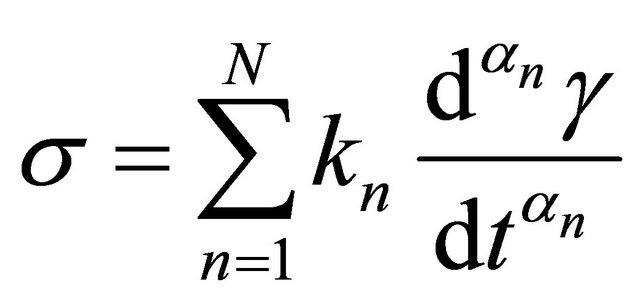 (4)
(4)
The Equation (4) can be rewritten in terms of fractional derivative (Riemann-Liouville approach) [7,11], as follows:
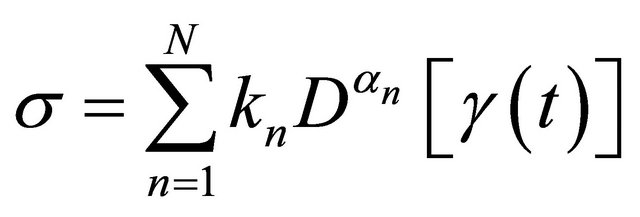 (5)
(5)
The Equation (5) was investigated by Song [12] et al., in order to describe a linear viscoelastic behavior of a food gum in terms of fractional derivative. The theory of fractional derivatives and Laplace transformers would be employed to manipulate these material functions that need to be obtained [6].
Then, one can write the fractional operator such as:
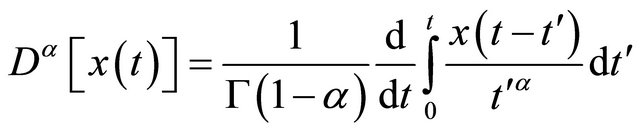 (6)
(6)
with, 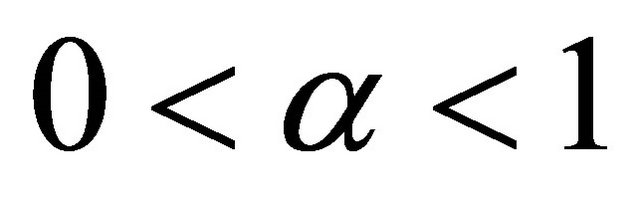 .
.
The Leibniz rule [6] may be used to differentiate the integral in Equation (6) and provides:
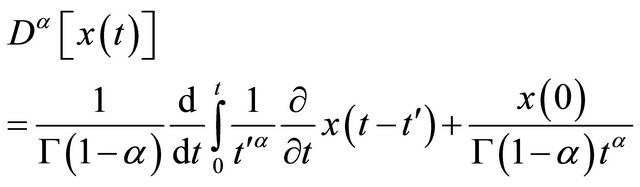 (7)
(7)
By applying the Laplace transform to Equation (7), the following expression is obtained [11]:
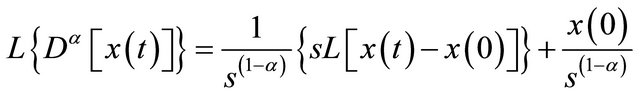 (8)
(8)
In accordance with Song [12] et al., a frequency-dependent complex modulus can be obtained and by decomposing into real and imaginary parts, the following expression is produced [12]:
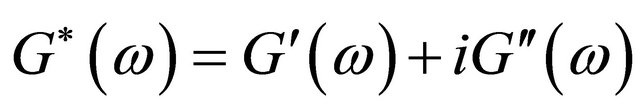 (9)
(9)
where,
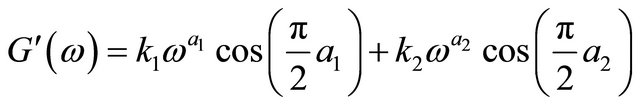 (10)
(10)
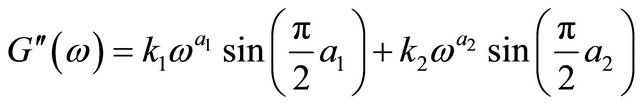 (11)
(11)
The dynamic viscosity, 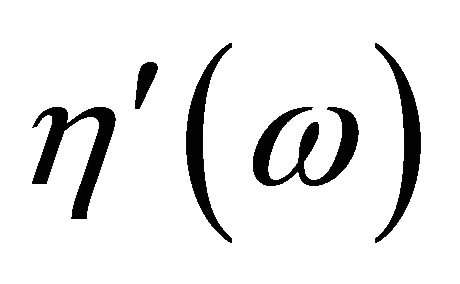 , and the out-of-phase component of the complex viscosity,
, and the out-of-phase component of the complex viscosity, 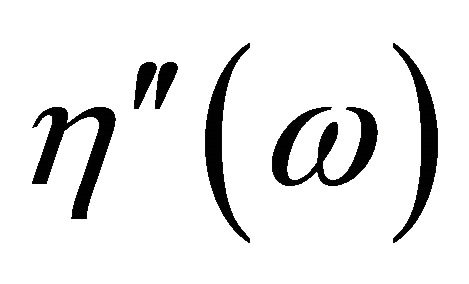 , can be obtained by the following relationships:
, can be obtained by the following relationships:
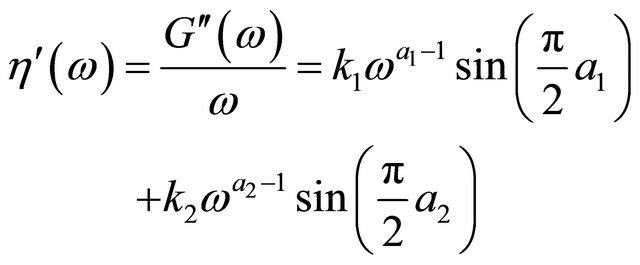 (12)
(12)
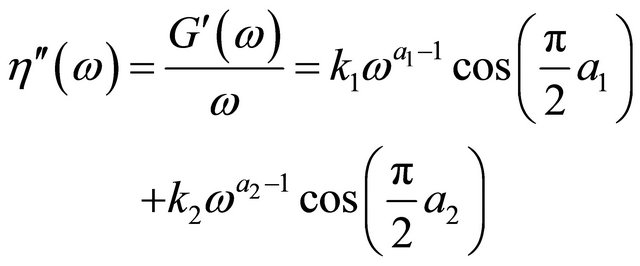 (13)
(13)
and  and
and 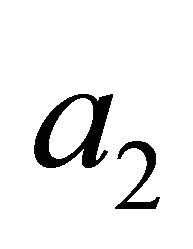 are parameters of a simplified model. These equations were used to simulate a linear viscoelastic behavior of a food gum since the constants in these equations be known.
are parameters of a simplified model. These equations were used to simulate a linear viscoelastic behavior of a food gum since the constants in these equations be known.
With this fact in mind, we have chosen a set of constants [11-13] in order to investigate, by means of numerical simulation, the viscoelastic behavior of the system. Some results are presented in the next section.
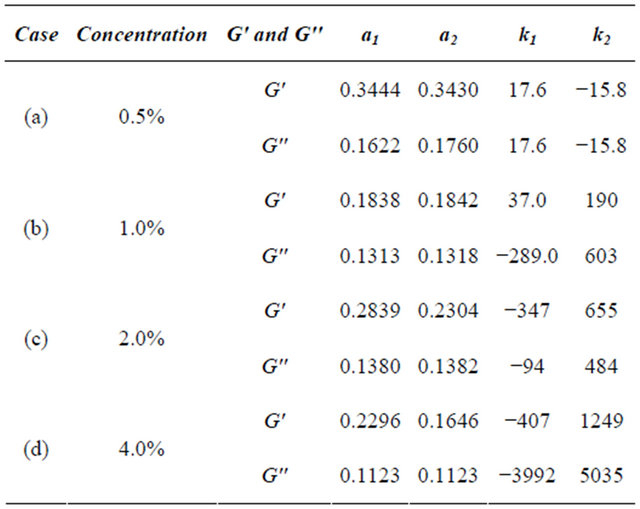
Table 2 shows the simulations cases with the model parameters. The parameters were obtained from the experimental data in the literature [11,12] and were determined by a least squares fit.
Table 2. Model parameters for the fractional calculus model.
4. Numerical Simulations Results
The numerical simulations were realized with the usage of the MATLAB®-MathWorks package and then by an algorithm developed in C++. The results show that the Storage Modulus increases with the frequency (Figures 1-4). Except in case (a), low concentration (Figure 1), the same occur with the Loss Modulus (Figures 2-4). On the other hand, for the sake of comparison with previous results presented in the literature, the Dynamic Viscosity and Out-of-phase Complex Viscosity tends to a fixed value, when the frequency increases (Figures 5-8). Besides, one can note that the Dynamic Viscosity is variable when the frequency is very low.
5. Discussion and Conclusions
In this article, we have investigated, by means of numerical simulations, the dynamic viscoelastic behavior of a food gum using a fractional calculus model. The fractional calculus was employed to make a quantitative description of the viscoelastic behavior based on paper of
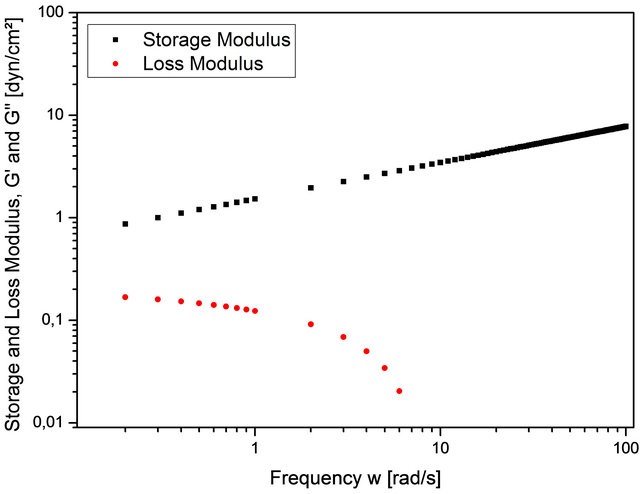
Figure 1. Case (a).

Figure 2. Case (b).

Figure 3. Case (c).
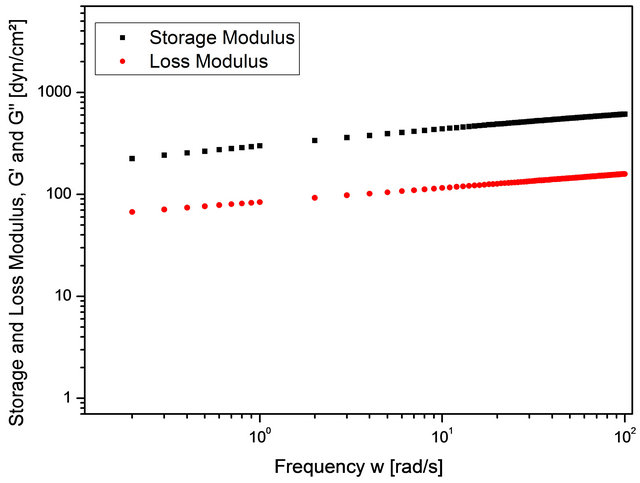
Figure 4. Case (d).
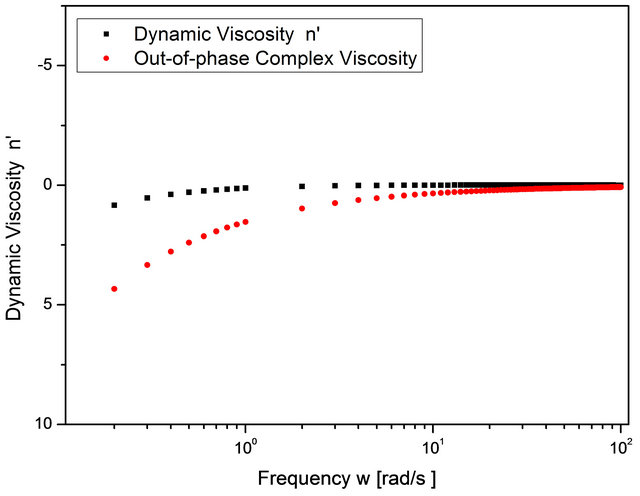
Figure 5. Case (a).
Ma and Barbosa-Cánovas [11]. Some different and curious results to the storage modulus (G') and dynamic viscosity (η') versus frequency (ω) were obtained when compared to the previous literature. We outline that the

Figure 6. Case (b).
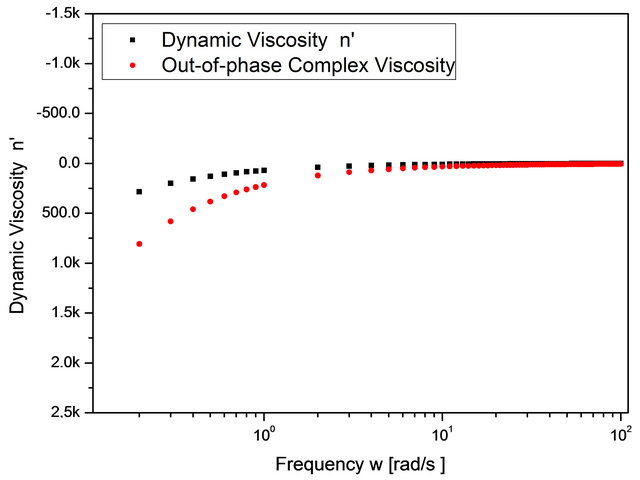
Figure 7. Case (c).

Figure 8. Case (d).
model parameters for the numerical simulations were obtained from the experimental data in the literature [11,12] and a future research should be realized in order to verify real physical meaning for the model parameters.
6. Acknowledgements
This project was supported by São Paulo Research Foundation (FAPESP) through grants n-2010/15824-0 and by a fellowship of the Dean’s Office for Research of the University of São Paulo (USP).
REFERENCES
- M. M. Luvielmo and A. R. P. Scamparini, “Goma Xantana: Produção, Recuperação, Propriedades e Aplicação,” Estudos Tecnológicos, Vol. 5, No. 1, 2009, pp. 50-67.
- R. B. Salah, S. Besbes, K. Chaari, A. Rhouma, H. Attia, C. Deroanne and C. Blecker, “Rheological and Physical Properties of Date Juice Palm By-Product (Phoenix dactylifera L.) and Commercial Xanthan Gums”, Journal of Texture Studies, Vol. 41, No. 2, 2010, pp. 125-138. doi:10.1111/j.1745-4603.2010.00217.x
- P. J. Whitcomb and C. W. Macosko, “Rheology of Xanthan Gum,” Journal of Rheology, Vol. 22, No. 5, 1978, pp. 493-505. doi:10.1122/1.549485
- J. A. Lopes da Silva, M. P. Gonçalves and M. A. Rao, “Viscoelastic Behavior of Mixtures of Locust Bean Gum and Pectin Dispersions,” Journal of Food Engineering, Vol. 18, No. 3, 1993, pp. 211-228. doi:10.1016/0260-8774(93)90087-Z
- M. Kobayashi and N. Nakahama, “Rheological Properties of Mixed Gels,” Journal of Texture Studies, Vol. 17, No. 2, 1986, pp. 161-174. doi:10.1111/j.1745-4603.1986.tb00402.x
- K. B. Oldham and J. Spanier, “The Fractional Calculus,” Academic Press, New York, 1974.
- S. A. David, J. L. Linares and E. M. J. A. Pallone, “Fractional Order Calculus: Historical Apologia, Basic Concepts and Some Applications,” Revista Brasileira de Ensino de Física, Vol. 33, No. 4, 2011, p. 4202. doi:10.1590/S1806-11172011000400002
- M. Caputo, “Distributed Order Differentia Equations Modeling Dieletric Induction and Diffusion,” Fractional Calculus and Applied Analysis, Vol. 4, No. 4, 2001, pp. 421- 442.
- B. Ross, “Fractional Calculus,” Mathematics Magazine, Vol. 50, No. 3, 1977, pp. 115-122. doi:10.2307/2689497
- M. Caputo and F. Mainardi, “Linear Models of Dissipation in Anelastic Solids,” Rivista del Nuovo Cimento, Vol. 1, No. 2, 1971, pp. 161-198. doi:10.1007/BF02820620
- L. Ma and G. V. Barbosa-Cánovas, “Simulating Viscoelastic Properties of Selected Food Gums and Gum Mixtures Using a Fractional Derivative Model,” Journal of Texture Studies, Vol. 27, No. 3, 2007, pp. 307-325. doi:10.1111/j.1745-4603.1996.tb00077.x
- K. W. Song, H. Y. Kuk and G. S. Chang, “Rheology of Concentrated Xanthan Gum Solutions: Oscillatory Shear Flow Behavior,” Korea-Australia Rheology Journal, Vol. 18, No. 2, 2006, pp. 67-81.
- R. L. Bagley, “Power Law and Fractional Calculus Model of Viscoelasticity,” AIAA Journal, Vol. 27, No. 10, 1989, pp. 1414-1417. doi:10.2514/3.10279

