Applied Mathematics
Vol.4 No.1A(2013), Article ID:27495,7 pages DOI:10.4236/am.2013.41A032
The Continuous Analogy of Newton’s Method for Solving a System of Linear Algebraic Equations
1School of Mathematics and Computer Science, National University of Mongolia, Ulan-Bator, Mongolia
2Joint Institute for Nuclear Research, Dubna, Moscow Region, Russia
Email: *chuka@jinr.ru
Received October 31, 2012; revised January 2, 2013; accepted January 9, 2013
Keywords: Continuous Analogy of Newton’s Method; Solving the System of Linear Algebraic Equations; Convergence; Choice of Iteration Parameter
ABSTRACT
We propose a continuous analogy of Newton’s method with inner iteration for solving a system of linear algebraic equations. Implementation of inner iterations is carried out in two ways. The former is to fix the number of inner iterations in advance. The latter is to use the inexact Newton method for solution of the linear system of equations that arises at each stage of outer iterations. We give some new choices of iteration parameter and of forcing term, that ensure the convergence of iterations. The performance and efficiency of the proposed iteration is illustrated by numerical examples that represent a wide range of typical systems.
1. Introduction
We consider a system of linear algebraic equations
 (1)
(1)
For a numerical solving of Equation (1) we consider an iterative process:
 (2)
(2)
Of course, the quality of iterative process Equation (2) essentially depends on the choices of matrix B and of iteration parameter 
Let H be a linear space of m-dimensional vectors. We will denote the Euclidean vector norm in H by , as well as the corresponding norm of matrices.
, as well as the corresponding norm of matrices.
Theorem 1.1. Let  Then a necessary and sufficient condition for the
Then a necessary and sufficient condition for the  to be decreasing
to be decreasing  is that
is that

Proof. From Equation (2) we obtain

Hence we have
 (3)
(3)
The assertion follows from (3).
The interval  we call τ-region of convergence of the iteration method (2). Thus we have to choose
we call τ-region of convergence of the iteration method (2). Thus we have to choose  from this region. Moreover, it is desirable that the
from this region. Moreover, it is desirable that the  to be optimal in some sense. Further we will use wellknown assertions to study the convergence of (2).
to be optimal in some sense. Further we will use wellknown assertions to study the convergence of (2).
Theorem 1.2. [1]. Let S be an m × m matrix. Then the successive approximations
 (4)
(4)
converge for each  and each
and each  if and only if
if and only if
 (5)
(5)
where  is a spectral radius of the matrix S.
is a spectral radius of the matrix S.
It is easy to show that the iteration process (2) can be rewritten as (4) with iteration matrix
 (6)
(6)
Here E is an m × m unit matrix.
Theorem 1.3. [2]. The iteration process (2) with parameter  given by
given by
 (7)
(7)
converges to  for any
for any . The following a posteriori estimate holds true:
. The following a posteriori estimate holds true:
 (8)
(8)
where

We call the nonzero value of  defined by (10) the optimal one in the sense that it yields the minimum value of functional
defined by (10) the optimal one in the sense that it yields the minimum value of functional .
.
2. The Continuous Analogy of Newton’s Method
The continuous analogy of Newton’s method is also applicable to (1) and leads to [2]
 (9a)
(9a)
 (9b)
(9b)
It should be mentioned that not only the convergence, but also the convergence rate of iteration (9) depends on the choice of the parameter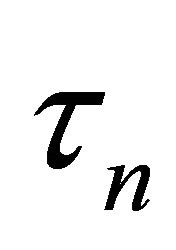 . We have the following:
. We have the following:
Lemma 2.1. The sufficient condition for 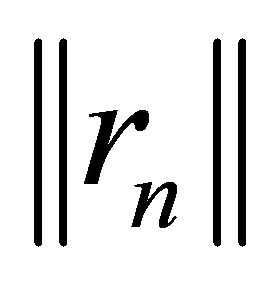 to be decreasing is
to be decreasing is 
Lemma 2.2. Suppose that  for all
for all . Then the iteration process (2) gives two-sided approximations to
. Then the iteration process (2) gives two-sided approximations to , i.e.,
, i.e.,

or

The proofs are immediately followed from the equalities

At each step of iterations one can solve the system (9a) by means of some iterative methods. We call this inner iteration. We consider the following decomposition of :
:

in which the matrix  is simple and invertible. For finding the correction
is simple and invertible. For finding the correction  we use inner iteration
we use inner iteration
 (10)
(10)
Theorem 2.3. Suppose that
 (11)
(11)
Then the inner iteration (10) converges and holds the following estimate
 (12)
(12)
Proof. The linear system (10) can be rewritten as
 (13)
(13)
By assumption (11) there exists  and the following series representation is valid
and the following series representation is valid
 (14)
(14)
Then from (13) it follows that
 (15)
(15)
In a similar way, from (10) we have
 (16)
(16)
From (15) and (16) immediately follows (14).
The estimate (12) means that the inner iteration (10) converges under condition (11). In real computations we have to terminate the inner iteration before convergence. We will restrict the number of inner iteration by k. Then the whole iteration process looks like:
 (17a)
(17a)
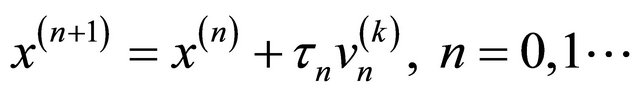 (17b)
(17b)
We now formulate the convergence theorems for these methods.
Theorem 2.4. Suppose that the condition (11) is satisfied and the iteration parameter  is given by
is given by
 (18)
(18)
Then the iteration process (17) converges for any  and for arbitrary chosen starting
and for arbitrary chosen starting .
.
Proof. We rewrite the iteration process (17) as (2) with

By Theorem 1.3, such a process converges if we choose 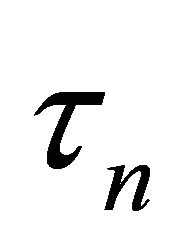 by (7), in which the
by (7), in which the  is replaced by
is replaced by .
.
Obviously the number k may be different for each n. From (12) it is evident, that it suffices to restrict the number of inner iteration only by k = 0 or 1, when the residual norm  is small enough.
is small enough.
Theorem 2.5. Suppose that the condition (11) is satisfied. Then the iteration process (17) with  converges for any
converges for any  and for arbitrary chosen starting
and for arbitrary chosen starting . The following inequality holds:
. The following inequality holds:
 (19)
(19)
Proof. From (17) we get

Using (11) and (16) we rewrite the last expression as
 (20)
(20)
If , then from (20) we obtain
, then from (20) we obtain

According to (11), we have . The convergence of (17) follows from (19).
. The convergence of (17) follows from (19).
Corollary 2.6. Let the condition (11) fulfill, and  is given by [3]
is given by [3]

Then the iteration (17) converges.
Remark 2.7. In proofs of Theorems 2.3-2.5 the condition (11) is essentially used. In particular, it may be fulfilled if the matrix A of the system (1) is a strongly diagonally dominant and A1 is chosen as

Theorem 2.8. Suppose that the condition (11) is satisfied and that the eigenvalues of matrix 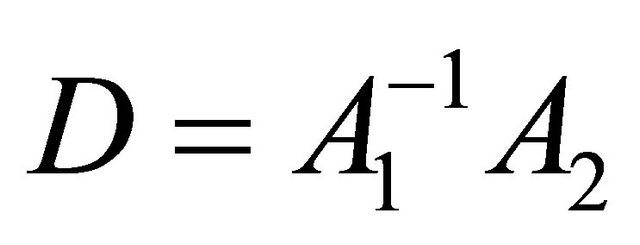 are real. Then the spectral radius of iteration matrices of the iterations (17) is decreasing with respect to k when
are real. Then the spectral radius of iteration matrices of the iterations (17) is decreasing with respect to k when .
.
Proof. The iterations (17) can be rewritten as (4) with iteration matrices
 (21)
(21)
We denote by  the eigenvalues of D. If
the eigenvalues of D. If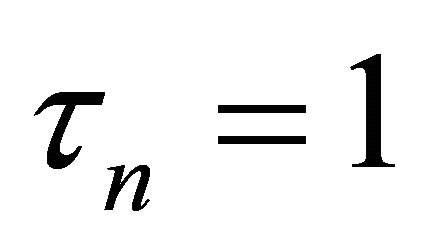 , then
, then

Therefore, we have

By virtue of (11) we obtain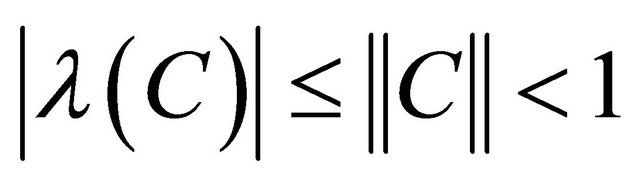 . Since the spectrums of matrices C and D coincide, we also have
. Since the spectrums of matrices C and D coincide, we also have

By definition we get

which is valid for all  Thus we have
Thus we have
 (22)
(22)
Obviously, from (21) it is clear that  is a continuous function of
is a continuous function of . Therefore, (22) is valid for
. Therefore, (22) is valid for .
.  The iteration (17) with a few small k represents a special interest from a computational view point. Moreover, it is worth to stay at (17) with k = 0 in detail. The iteration (17) with k = 0 and
The iteration (17) with a few small k represents a special interest from a computational view point. Moreover, it is worth to stay at (17) with k = 0 in detail. The iteration (17) with k = 0 and  leads to the well-known Jacobi iteration with relaxation parameter
leads to the well-known Jacobi iteration with relaxation parameter . It is also known that [1] the Jacobi method with optimal relaxation parameter
. It is also known that [1] the Jacobi method with optimal relaxation parameter
 (23)
(23)
converges under the assumption that the Jacobi matrix  has real eigenvalues and spectral radius less than one. Here by
has real eigenvalues and spectral radius less than one. Here by  and
and ![]() denoted are the smallest and largest eigenvalues of B. Fortunately, we can prove the convergence of Jacobi method with relation parameter under a mild condition than the above mentioned assumption. Namely, we have.
denoted are the smallest and largest eigenvalues of B. Fortunately, we can prove the convergence of Jacobi method with relation parameter under a mild condition than the above mentioned assumption. Namely, we have.
Corollary 2.9. Suppose that the condition (11) is satisfied. Then the Jacobi method with relaxation parameter:
 (24)
(24)
converges for any starting.
From (24) it is clear that the relaxation parameter changes depending on n. Therefore the iteration (17) with k = 0, and  and with
and with  given by (24) we call nonstationary Jacobi method with optimal relaxation parameters. The iteration (17) with k = 0 and with a lower triangular matrix
given by (24) we call nonstationary Jacobi method with optimal relaxation parameters. The iteration (17) with k = 0 and with a lower triangular matrix  leads to GaussSeidel with one parameter.
leads to GaussSeidel with one parameter.
The Formula (18) can be rewritten as:
 (25)
(25)
where  From this it is clear that
From this it is clear that  as
as . This means that whole iteration (17) with the parameter given by (18) converges quadratically in the limit.
. This means that whole iteration (17) with the parameter given by (18) converges quadratically in the limit.
Since  as
as , then τ-region of convergence for iterations (17) leads to
, then τ-region of convergence for iterations (17) leads to

The number of outer iteration n depends on the number of inner iteration k, i.e., . In general, n is a decreasing function of k, i.e.,
. In general, n is a decreasing function of k, i.e., 
On the other hand, the iteration (17) can be considered as a defect correction iteration [1]
![]() (26)
(26)
where  defined by
defined by
 (27)
(27)
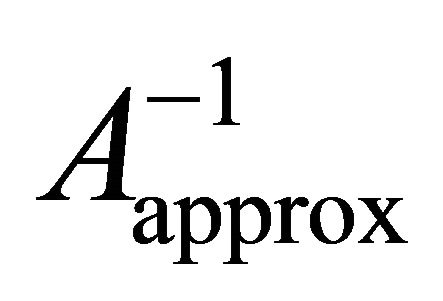 is a reasonable approximation to
is a reasonable approximation to  since
since
 (28)
(28)
for large k. The choice of parameter  given by (25) allows us to decrease the residual norm from iteration to iteration. By this reason we call (26) as a minimal defect (or residual) correction iteration.
given by (25) allows us to decrease the residual norm from iteration to iteration. By this reason we call (26) as a minimal defect (or residual) correction iteration.
From (26) it follows that
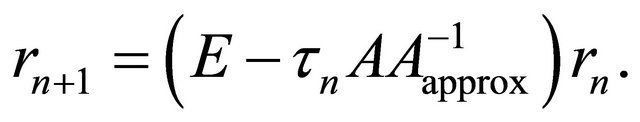 (29)
(29)
From (29) and , it follows that
, it follows that

Therefore we have

This means that the spectral radius of matrix  depends on the number of inner iteration k, i.e.,
depends on the number of inner iteration k, i.e., . Therefore we have
. Therefore we have 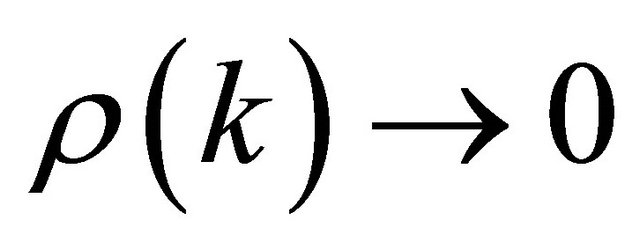 as
as , because
, because  as
as  and from (11)
and from (11)

Above we considered the cases, where the inner iteration number k is fixed at each outer iteration. It is desirable that the termination criterion for the inner iteration must be chosen carefully to preserve the superlinear convergence rate of the outer iteration. We stay at this problem in more detail. When , the iteration (17) is, indeed, inexact Newton (IN) method for (1). Therefore, iteration (17) with parameter
, the iteration (17) is, indeed, inexact Newton (IN) method for (1). Therefore, iteration (17) with parameter  given by formula (18) we call inexact damped Newton method (IDN). According to IN method [4,5], we must choose
given by formula (18) we call inexact damped Newton method (IDN). According to IN method [4,5], we must choose  and continue the inner iteration until satisfy the condition
and continue the inner iteration until satisfy the condition
 (30)
(30)
Thus (30) is a stopping criterion for inner iteration (17a). There are several choices of forcing term  in inexact Newton method [4-6]. For examples, in [6] two choices of
in inexact Newton method [4-6]. For examples, in [6] two choices of  were proposed:
were proposed:
 (31)
(31)
with

and
 (32)
(32)
Since we have formula (18) for , one can use the second choice (14) with no additional calculations. We can also use formula for
, one can use the second choice (14) with no additional calculations. We can also use formula for  [7]. Therefore, according to (32), we get
[7]. Therefore, according to (32), we get
 (33)
(33)
3. Numerical Results
The quality of the proposed iteration was checked up for numerous examples. We express the matrix A as

where , and AL, AU are lower and upper triangular matrices, respectively. All examples are calculated with an accuracy
, and AL, AU are lower and upper triangular matrices, respectively. All examples are calculated with an accuracy .
.
The numerical calculations are performed on Acer, CPU 1.8 GHz, 1 GB RAM, and using a software MATLAB R2007a for the Windows XP system.
Example 1. We consider a system of Equation (1) with matrix A and f given by
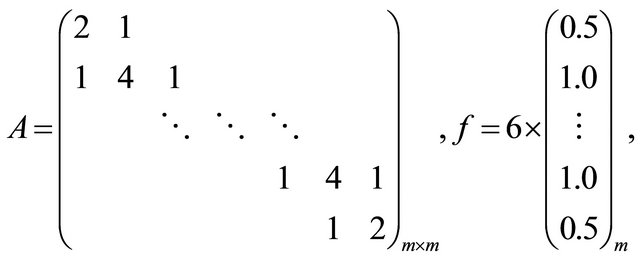
which was solved by the proposed iteration method (17), (18). For comparison, it was solved by Jacobi and successive over relaxation (SOR) iterations with a parameter .
.
Example 2.

Example 3.

Example 4.

where  and
and
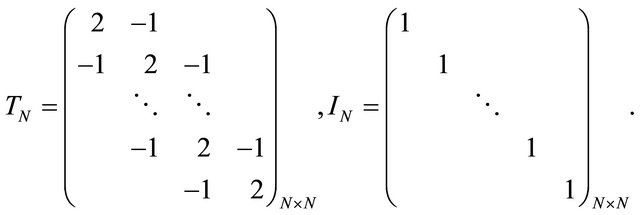
Such a system arises in discretization of two dimensional Poisson equation [8]:

The exact value of  is [9]
is [9]
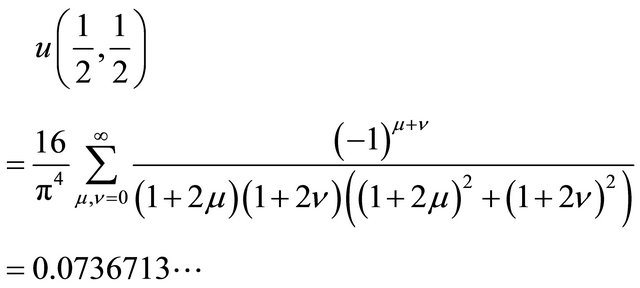 (34)
(34)
The properties of matrix for examples 1-4 are shown in Table 1. From this we see that the considered examples represent a wide range of typical systems.
The numbers of Jacobi and SOR iterations versus the dimension m of example 1 are presented in Table 2. Here k is the number of inner iteration in (17) (18). From this example we see that the proposed iteration (17), (18) can compete with SOR iteration with optimal relaxation parameter and seem to be superior to the Jacobi iteration. The behavior of the iteration parameter  given by (18) at m = 10 is explained in Table 3. From this we see that the iteration parameter
given by (18) at m = 10 is explained in Table 3. From this we see that the iteration parameter  tends to 1 as k increases.
tends to 1 as k increases.
The number n of outer iteration (17), (18) with fixed number k of inner iterations, and CPU time for examples 2 and 3 are shown in Table 4. From this we see that they are in example 2 considerable less than example 3. This explained by reason that matrix of this system has a strictly diagonally dominant. The number n of outer iteration, the total number k of inner iteration when forcing terms  was chosen by formulas (32) and (33), and CPU time are displayed in Table 5. Here it is observed similar situations as in the previous case.
was chosen by formulas (32) and (33), and CPU time are displayed in Table 5. Here it is observed similar situations as in the previous case.
Monotonic convergence of the calculated values 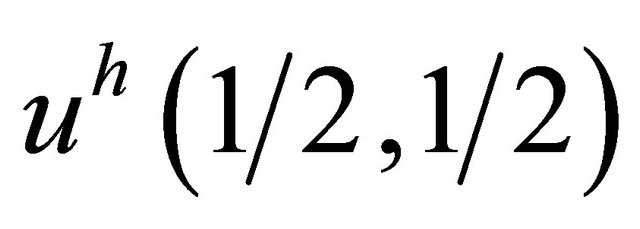 to exact value (34) versus the dimension N of the example 4 is shown in Table 6. The number n of outer iteration with fixed and unfixed number k of inner iteration and CPU time versus the dimension N of the example 4 are presented in Tables 7 and 8, respectively.
to exact value (34) versus the dimension N of the example 4 is shown in Table 6. The number n of outer iteration with fixed and unfixed number k of inner iteration and CPU time versus the dimension N of the example 4 are presented in Tables 7 and 8, respectively.
Table 1. The properties of matrix for examples 1-4.

Table 2. The numbers of Jacobi and SOR iterations versus the dimension ![]() of example 1. Here
of example 1. Here  is the number of inner iteration in (17), (18).
is the number of inner iteration in (17), (18).

Table 3. The behavior of the iteration parameter τn given by (18) for example 1. Here n and k are the numbers of outer and inner iterations in (17), respectively.

Table 4. The number n of outer iteration with fixed number k of inner iteration, and CPU time CT for examples 2 and 3.

Table 5. The number n of outer iteration, the total number k of inner iteration when forcing terms ηn was chosen by formulas (32) and (33), and CPU time CT.

4. Conclusions
Our method with inner iteration is quadratically convergent and therefore it can compete with other iterations such as SOR with an optimal relaxation parameter for a strictly diagonally dominant system. Moreover, our method is also applicable not only for the system with a strictly diagonal dominant matrix, but also for system, the matrix of which is not Hermitian and positive definite.
This work was partially sponsored by foundation for science and technology of Ministry of Education, Culture, and Science (Mongolia).
Table 6. A comparison of the calculated values u(1/2, 1/2) and an exact value (34) versus the dimension N of the example 4.

Table 7. The number n of outer iteration with fixed number k of inner iteration, and CPU time CT versus the dimension N of the example 4.

Table 8. The number n of outer iteration with unfixed number k of inner iteration, the itration parameter τn, and CPU time CT versus the dimension N of the example 4.

O. Chuluunbaatar acknowledges a financial support from the RFBR Grant No. 11-01-00523, and the theme 09-6-1060-2005/2013 “Mathematical support of experimental and theoretical studies conducted by JINR”.
REFERENCES
- R. Kress, “Numerical Analysis,” Springer-Verlag, Berlin, 1998. doi:10.1007/978-1-4612-0599-9
- T. Zhanlav, “On the Iteration Method with Minimal Defect for Solving a System of Linear Algebraic Equations,” Scientific Transaction, No. 8, 2001, pp. 59-64.
- T. Zhanlav and I. V. Puzynin, “The Convergence of Iterations Based on a Continuous Analogy Newton’s Method,” Journal of Computational Mathematics and Mathematical Physics, Vol. 32, No. 6, 1992, pp. 729-737.
- R. S. Dembo, S. C. Eisenstat and T. Steihaug, “Inexact Newton Methods,” SIAM Journal on Numerical Analysis, Vol. 19, No. 2, 1982, pp. 400-408. doi:10.1137/0719025
- H. B. An, Z. Y. Mo and X. P. Liu, “A Choice of Forcing Terms in Inexact Newton Method,” Journal of Computational and Applied Mathematics, Vol. 200, No. 1, 2007, pp. 47-60. doi:10.1016/j.cam.2005.12.030
- T. Zhanlav, O. Chuluunbaatar and G. Ankhbayar, “Relationship between the Inexact Newton Method and the Continuous Analogy of Newton Method,” Revue D’Analyse Numerique et de Theorie de L’Approximation, Vol. 40, No. 2, 2011, pp. 182-189.
- T. Zhanlav and O. Chuluunbaatar, “The Local and Global Convergence of the Continuous Analogy of Newton’s Method,” Bulletin of PFUR, Series Mathematics, Information Sciences, Physics, No. 1, 2012, pp. 34-43.
- J. W. Demmel, “Applied Numerical Linear Algebra,” SIAM, Philadelphia, 1997, pp. 265-360. doi:10.1137/1.9781611971446
- W. Hackbusch, “Elliptic Differential Equations: Theory and Numerical Treatment,” Springer Series in Computational Mathematics, Vol. 18, Springer, Berlin, 1992.
NOTES
*Corresponding author.

