Applied Mathematics
Vol.3 No.9(2012), Article ID:22999,4 pages DOI:10.4236/am.2012.39147
An Instability Result to a Certain Vector Differential Equation of the Sixth Order
Department of Mathematics, Faculty of Sciences, Yüzüncü Yıl University, Van, Turkey
Email: cemtunc@yahoo.com
Received August 12, 2012; revised September 12, 2012; accepted September 17, 2012
Keywords: Vector; Nonlinear Differential Equation; Sixth Order; Lyapunov-Krasovskii Functional; Instability; Delay
ABSTRACT
The nonlinear vector differential equation of the sixth order with constant delay is considered in this article. New criteria for instability of the zero solution are established using the Lyapunov-Krasovskii functional approach and the differential inequality techniques. The result of this article improves previously known results.
1. Introduction
In 2008, E. Tunç and C. Tunç [1] proved a theorem on the instability of the zero solution of the sixth order nonlinear vector differential equation
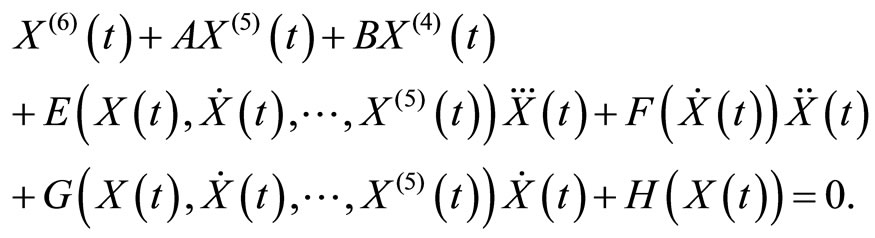 (1)
(1)
The objective of this article is to investigate the instability of the zero solution of the sixth order nonlinear vector differential equation with constant delay, 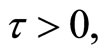
 (2)
(2)
by the Lyapunov-Krasovskii functional approach under assumptions  A and B are constant
A and B are constant  - symmetric matrices; E, F and G are continuous
- symmetric matrices; E, F and G are continuous  - symmetric matrix functions depending, in each case, on the arguments shown;
- symmetric matrix functions depending, in each case, on the arguments shown; 
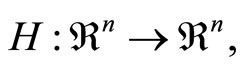 and H is continuous. Let
and H is continuous. Let  denote the Jacobian matrix corresponding to
denote the Jacobian matrix corresponding to 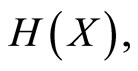 that is,
that is,
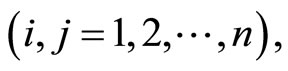

where 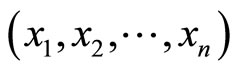 and
and 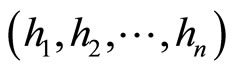 are the components of X and H, respectively. We also assume that the Jacobian matrix
are the components of X and H, respectively. We also assume that the Jacobian matrix 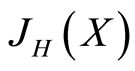 exists and is continuous.
exists and is continuous.
It should be noted that Equation (2) is the vector version for systems of real nonlinear differential equations of the sixth order
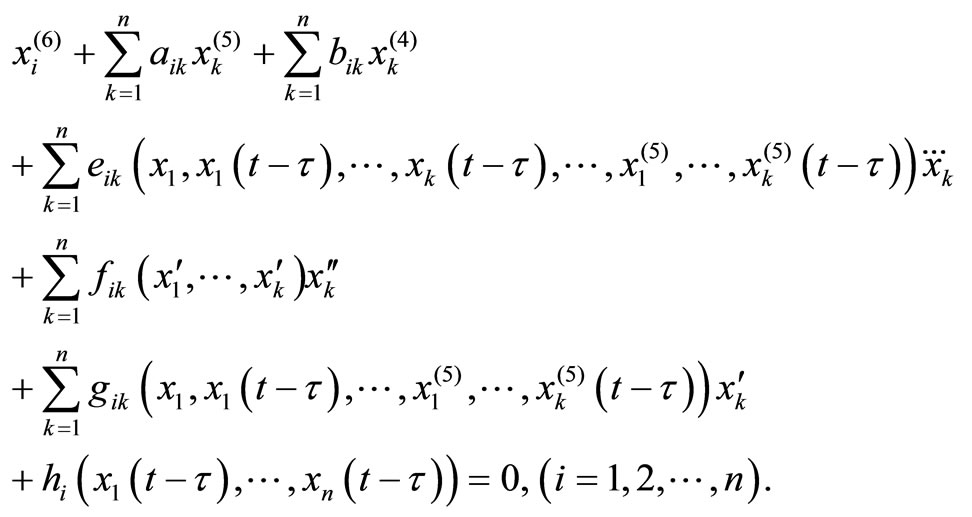
We can write Equation (2) in the system form
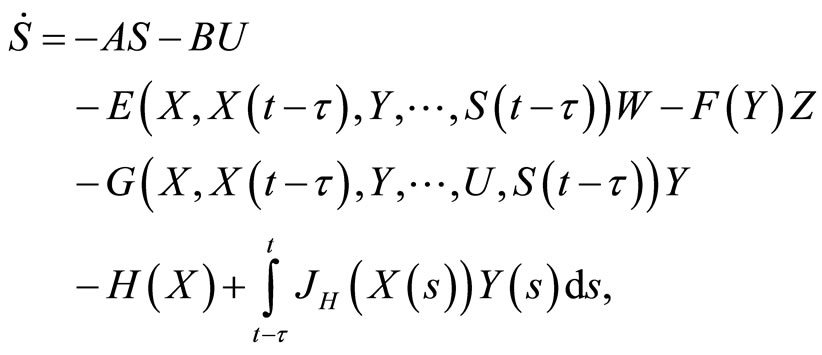 (3)
(3)
which is obtained from (2) by setting 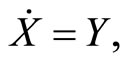

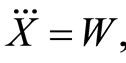
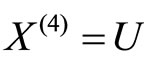 and
and 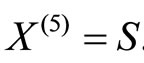 Throughout what follows
Throughout what follows 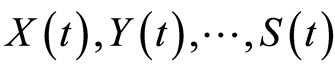 are abbreviated as
are abbreviated as  respectively.
respectively.
Consider, in the case 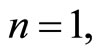 the linear differential equation of the sixth order:
the linear differential equation of the sixth order:
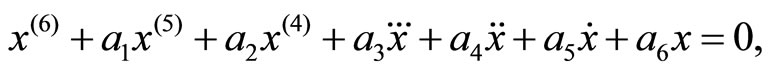 (4)
(4)
where 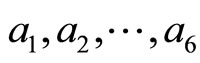 are real constants.
are real constants.
It is known from the qualitative properties of solutions of Equation (4) that the zero solution of this equation is unstable if and only if the associated auxiliary equation
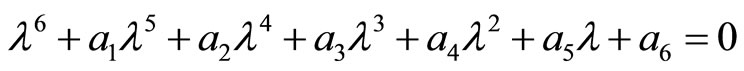 (5)
(5)
has at the least one root with a positive real part. The existence of such a root depends on (though not always all of) the coefficients 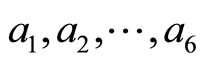 in Equation (5). Basing on the relations between the roots and the coefficients of Equation (5) it can be said that if
in Equation (5). Basing on the relations between the roots and the coefficients of Equation (5) it can be said that if
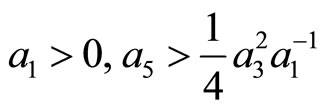
or
 (6)
(6)
then at the least one root of Equation (5) has a positive real part for arbitrary values of 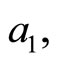
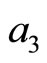 and
and 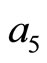 or
or 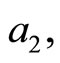
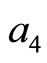 and
and 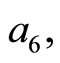 respectively.
respectively.
It should be noted that Equation (2) is an n-dimensional generalization of Equation (4), and when we establish our assumptions, we will take into consideration the estimates in (6). The symbol 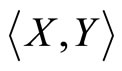 corresponding to any pair X, Y in
corresponding to any pair X, Y in 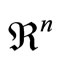 stands for the usual scalar product
stands for the usual scalar product 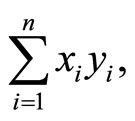 and
and 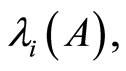
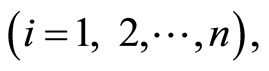 are the eigenvalues of the
are the eigenvalues of the 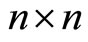 -matrix
-matrix 
It is worth mentioning that using the Lyapunov functions or Lyapunov-Krasovskii functionals and based on the Krasovskii properties [2], the instability of the solutions of the sixth order nonlinear scalar differential equations and the sixth order vector differential equations without delay were discussed by Ezeilo [3], Tejumola [4], Tiryaki [5] and Tunç [6-13]. The aim of this paper is to improve the results of ([1,3]) form the scalar and vector differential equations without delay to the sixth order nonlinear vector differential equation with delay, Equation (2).
2. Main Result
First, we give an algebraic result.
Lemma. Let D be a real symmetric 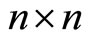 -matrix. Then for any
-matrix. Then for any 
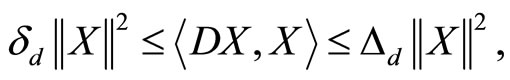
where 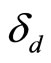 and
and 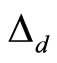 are the least and greatest eigenvalues of
are the least and greatest eigenvalues of 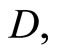 respectively (Bellman [14]).
respectively (Bellman [14]).
Let 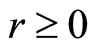 be given, and let
be given, and let  with
with
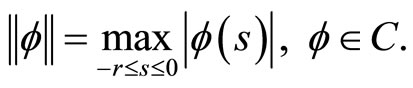
For 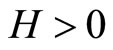 define
define 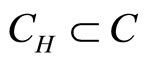 by
by
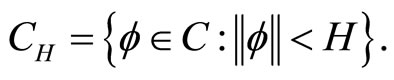
If 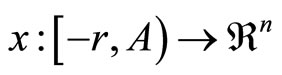 is continuous,
is continuous,  then, for each t in
then, for each t in 
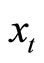 in C is defined by
in C is defined by

Let G be an open subset of C and consider the general autonomous delay differential system with finite delay
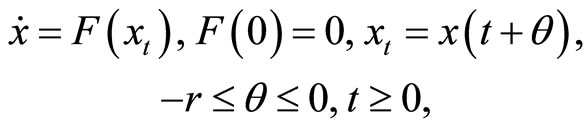
where 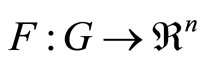 is continuous and maps closed and bounded sets into bounded sets. It follows from these conditions on F that each initial value problem
is continuous and maps closed and bounded sets into bounded sets. It follows from these conditions on F that each initial value problem
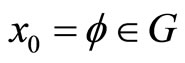
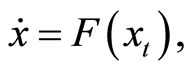
has a unique solution defined on some interval 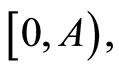
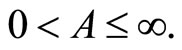 This solution will be denoted by
This solution will be denoted by 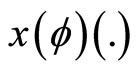 so that
so that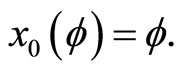
Definition. The zero solution, 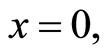 of
of 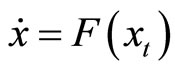 is stable if for each
is stable if for each 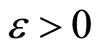 there exists
there exists 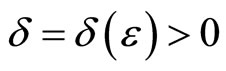 such that
such that 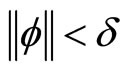 implies that
implies that 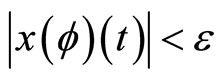 for all
for all 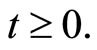 The zero solution is said to be unstable if it is not stable.
The zero solution is said to be unstable if it is not stable.
The result to be proved is the following theorem.
Theorem. In addition to the basic assumptions imposed on A, B, E, F, G and H that appear in Equation (2), we suppose that there are constants 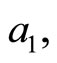
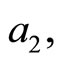
 and
and 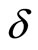 such that the following conditions hold:
such that the following conditions hold:
The matrices A, B, E, F, G and 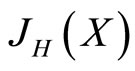 are symmetric and
are symmetric and 
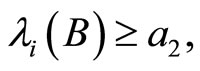
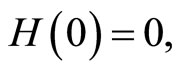
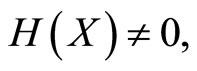 when
when 
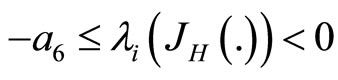 and
and
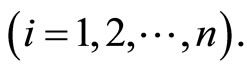

If
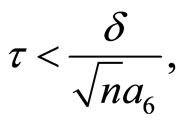
then the zero solution of Equation (2) is unstable.
Remark. It is worth mentioning that there is no sign restriction on eigenvalues of F, and it is obvious that for the delay case our assumptions also have a very simple form and their applicability can be easily verified.
Proof. Define a Lyapunov-Krasovskii functional
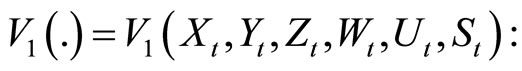
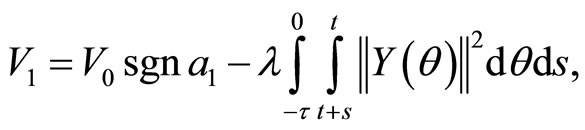
where
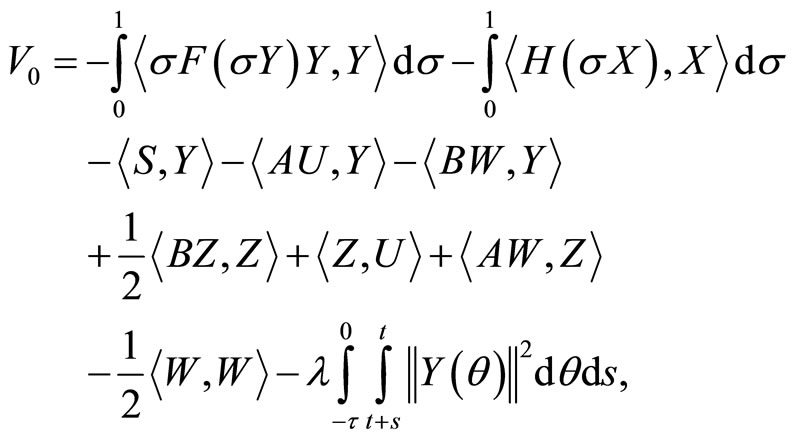
where 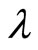 is a certain positive constant and will be determined later in the proof.
is a certain positive constant and will be determined later in the proof.
It follows that

and
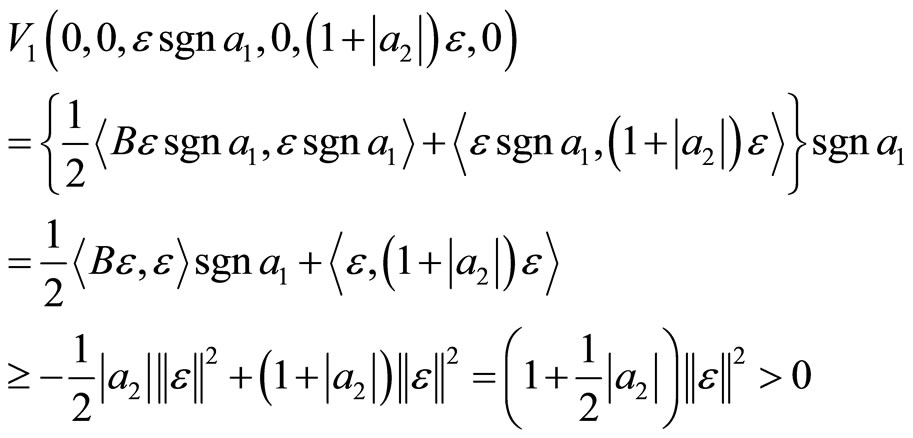
for all arbitrary 
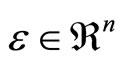 so that the property
so that the property 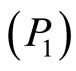 of Krasovskii [2] holds.
of Krasovskii [2] holds.
Using a basic calculation, the time derivative of 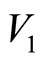 along solutions of (3) results in
along solutions of (3) results in
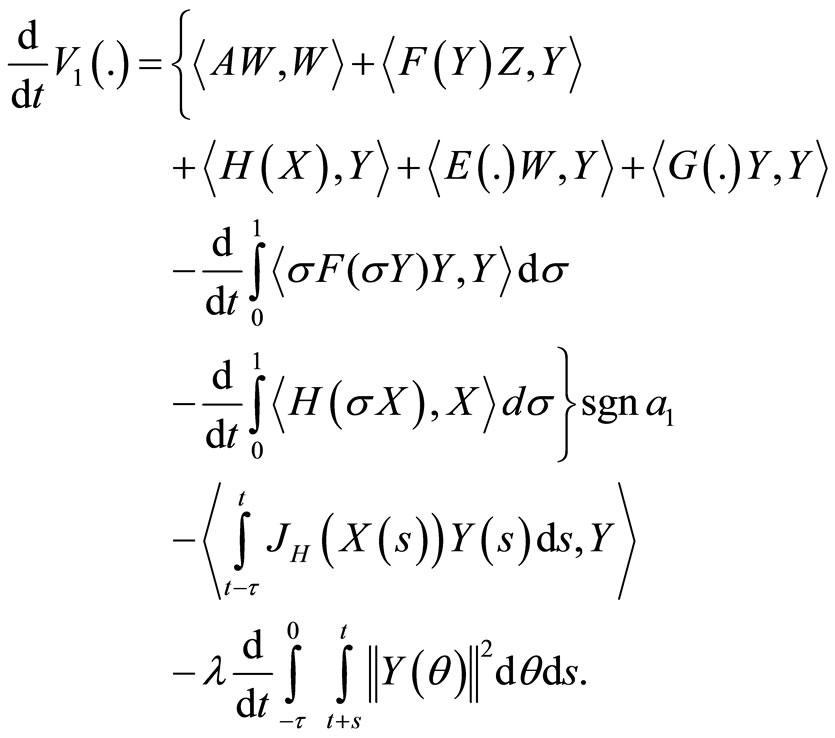
The following estimates can be easily calculated:
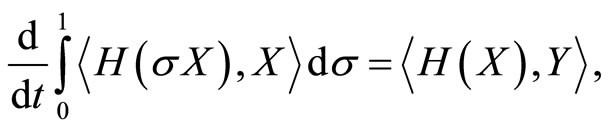
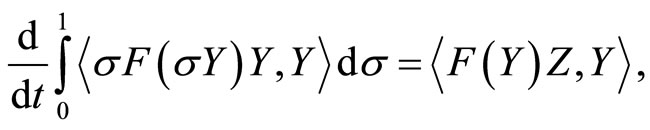
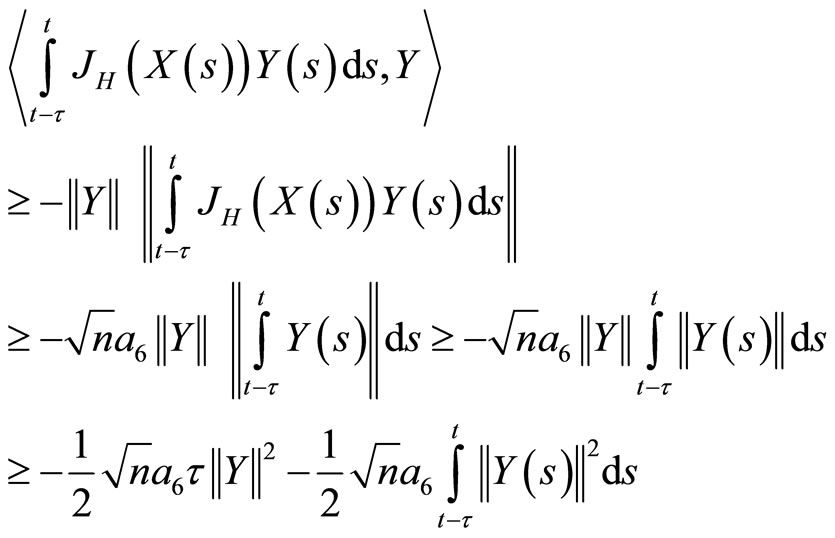
and

so that
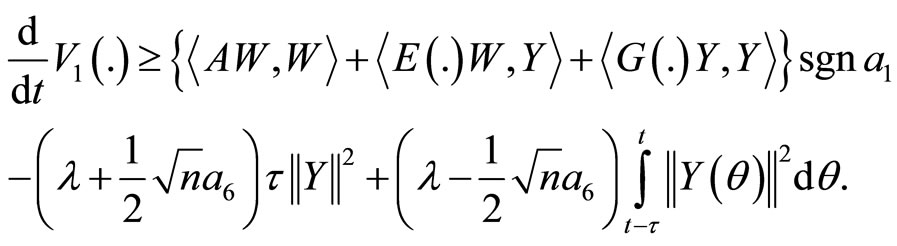
Using the assumptions of the theorem, we get
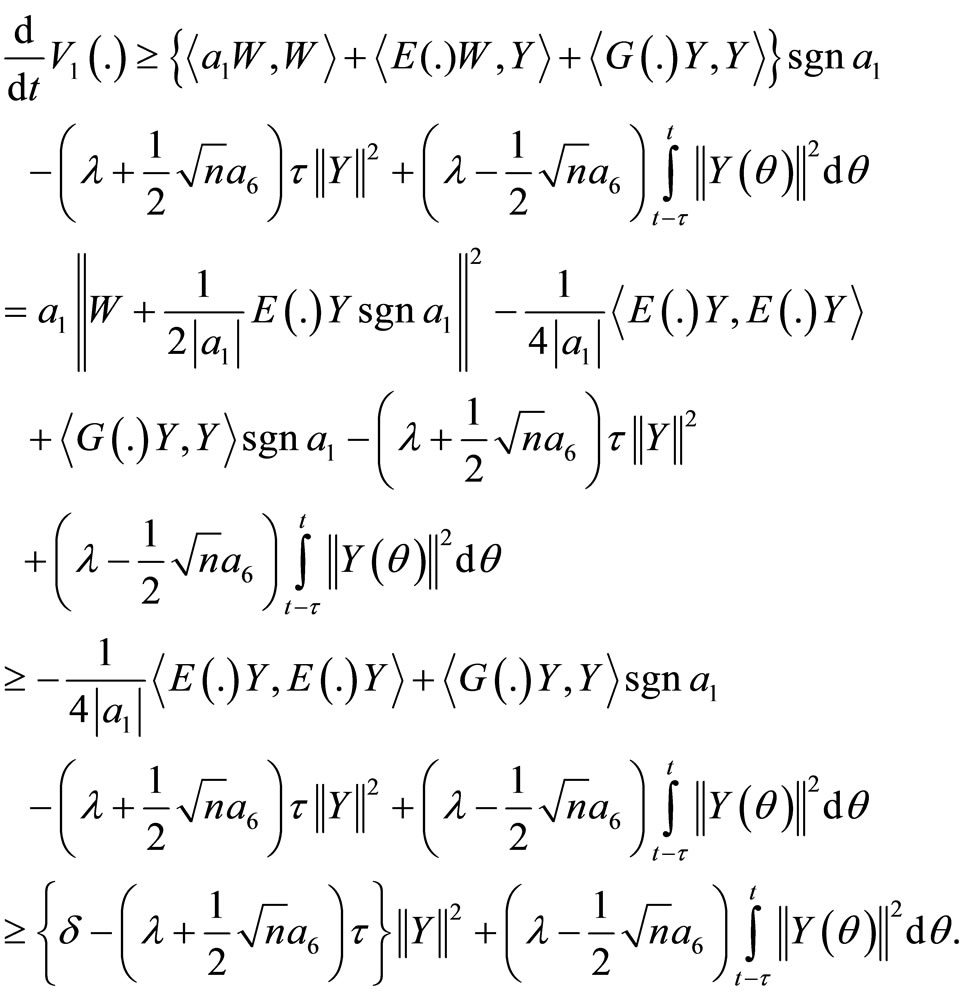
Let
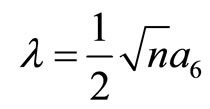
so that
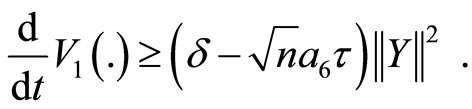
If 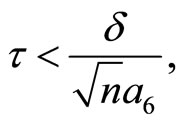 then, for a positive constant
then, for a positive constant  we have
we have
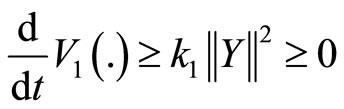
so that the property  of Krasovskii [2] holds.
of Krasovskii [2] holds.
It is seen that
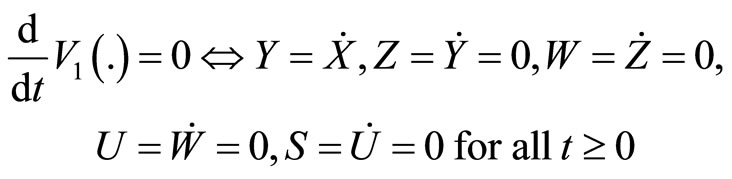
so that
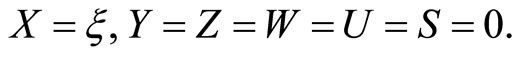
Using these estimates in (3) and the assumptions of the theorem, we get 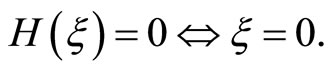 Thus, we have
Thus, we have
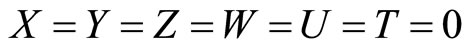 for all
for all 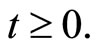 So that the property
So that the property  of Krasovskii [2] holds.
of Krasovskii [2] holds.
The proof of the theorem is complete.
Example. For the particular case 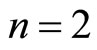 in Equation (2), we have
in Equation (2), we have
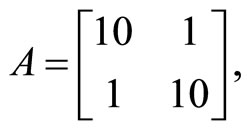

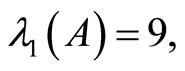


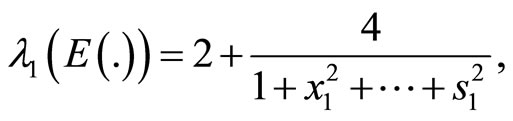

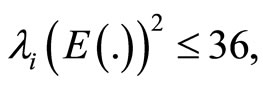
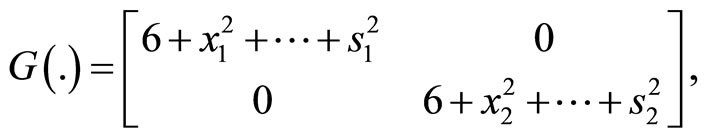
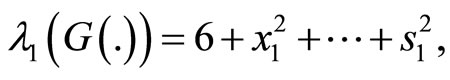
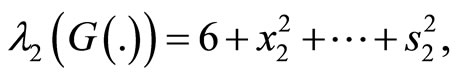

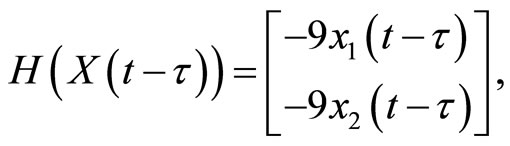
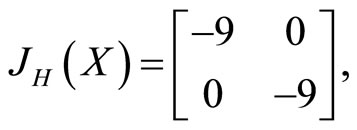

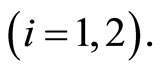

If
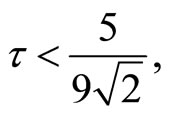
then all the assumptions of the theorem hold.
REFERENCES
- E. Tunç and C. Tunç, “On the Instability of Solutions of Certain Sixth-Order Nonlinear Differential Equations,” Nonlinear Stud, Vol. 15, No. 3, 2008, pp. 207-213.
- N. N. Krasovskii, “Stability of Motion. Applications of Lyapunov’s Second Method to Differential Systems and Equations with Delay,” Stanford University Press, Stanford, 1963.
- J. O. C. Ezeilo, “An Instability Theorem for a Certain Sixth Order Differential Equation,” Journal of the Australian Mathematical Society, Vol. 32, No. 1, 1982, pp. 129-133. doi:10.1017/S1446788700024460
- H. O. Tejumola, “Instability and Periodic Solutions of Certain Nonlinear Differential Equations of Orders Six and Seven,” Proceedings of the National Mathematical Centre, National Mathematical Center, Abuja, 2000.
- A. Tiryaki, “An Instability Theorem for a Certain Sixth Order Differential Equation,” Indian Journal of Pure and Applied Mathematics, Vol. 21, No. 4, 1990, pp. 330-333.
- C. Tunç, “An Instability Result for Certain System of Sixth Order Differential Equations,” Applied Mathematics and Computation, Vol. 157, No. 2, 2004, pp. 477-481. doi:10.1016/j.amc.2003.08.046
- C. Tunç, “On the Instability of Certain Sixth-Order Nonlinear Differential Equations,” Electronic Journal of Differential Equations, No. 117, 2004, p. 6.
- C. Tunç, “On the Instability of Solutions to a Certain Class of Non-Autonomous and Non-Linear Ordinary Vector Differential Equations of Sixth Order,” Albanian Journal of Mathematics, Vol. 2, No. 1, 2008, pp. 7-13.
- C. Tunç, “A Further Result on the Instability of Solutions to a Class of Non-Autonomous Ordinary Differential Equations of Sixth Order,” Applications & Applied Mathematics, Vol. 3, No. 1, 2008, pp. 69-76.
- C. Tunç, “New Results about Instability of Nonlinear Ordinary Vector Differential Equations of Sixth and Seventh Orders,” Dynamics of Continuous, Discrete and Impulsive Systems, Series A: Mathematical Analysis, Vol. 14, No. 1, 2007, pp. 123-136.
- C. Tunç, “Instability for a Certain Functional Differential Equation of Sixth Order,” Journal of the Indonesian Mathematical Society, Vol. 17, No. 2, 2011, pp. 123-128.
- C. Tunç, “Instability Criteria for Solutions of a Delay Differential Equation of Sixth Order,” Journal of Advanced Research in Applied Mathematics, Vol. 4, No. 2, 2012, pp. 1-7.
- C. Tunç, “An Instability Theorem for a Certain Sixth Order Nonlinear Delay Differential Equation,” Journal of the Egyptian Mathematical Society, 2012, in Press.
- R. Bellman, “Introduction to Matrix Analysis,” 2nd Edition, In: G. Golub, Ed., Classics in Applied Mathematics, Society for Industrial and Applied Mathematics (SIAM), Philadelphia, 1997.

