Applied Mathematics
Vol. 3 No. 4 (2012) , Article ID: 18881 , 6 pages DOI:10.4236/am.2012.34051
A Privacy-Preserving Grouping Proof Protocol Based on ECC with Untraceability for RFID
1Department of Electrical Engineering, Chang Gung University, Tao-Yuan, Chinese Taipei
2Department of Information Management, Chang Gung University, Tao-Yuan, Chinese Taipei
Email: curtis2gm@gmail.com,{ansel, *lueh, changher}@mail.cgu.edu.tw
Received February 14, 2012; revised March 12, 2012; accepted March 19, 2012
Keywords: ECC; RFID; Grouping Proof; Privacy-Preserving
ABSTRACT
An RFID (Radio-Frequency IDentification) system provides the mechanism to identify tags to readers and then to execute specific RFID-enabled applications. In those applications, secure protocols using lightweight cryptography need to be developed and the privacy of tags must be ensured. In 2010, Batina et al. proposed a privacy-preserving grouping proof protocol for RFID based on ECC (Elliptic Curve Cryptography) in public-key cryptosystem. In the next year, Lv et al. had shown that Batina et al.’s protocol was insecure against the tracking attack such that the privacy of tags did not be preserved properly. Then they proposed a revised protocol based on Batina et al.’s work. Their revised protocol was claimed to have all security properties and resisted tracking attack. But in this paper, we prove that Lv et al.’s protocol cannot work properly. Then we propose a new version protocol with some nonce to satisfy the functions of Batina et al.’s privacy-preserving grouping proof protocol. Further we try the tracing attack made by Lv et al. on our protocol and prove our protocol can resist this attack to recover the untraceability.
1. Introduction
An RFID system provides an identification mechanism to identify objects, having RFID tags attached, to reader by communicating over an insecure RF-channel. The basic architecture of an RFID system is combined with a tag, a reader and a backend database server. An RFID tag is a small and cheap device which consists of an IC chip and an antenna for radio communications. RFID tags provide more functionalities as barcodes. Each tag has memory to store more information than barcode. And tags can execute the communication process of answering the request of a reader. An RFID reader is used for querying, reading and writing tag data in no line-of-sight, contactlessly and bulkily. All the data between tags and reader need to send to backend database server. Therefore, RFID is considered to be a suitable replacement for barcodes to reduce the cost of store managements and goods distribution, and to increase the asset visibility.
Owing to RFID is based on radio waves, a kind of unsecured communication channel, RFID system needs secure protocol to protect tag’s identify information. Especially when a tag is linked to a person, then the tracing of a tag is equivalent to the tracing of a person. In that case, tag’s privacy will become a critical security issue in the RFID system.
In 2004, Juels [1] introduced the concept of RFID yoking proof. The proof means that two RFID tags have been scanned simultaneously. The RFID yoking proof also named grouping proof which is designed for any application that requires proving two or more entities are present. These applications of grouping proof are increasing in modern life such as delivering some related medication in groups, launching some kind of weapon system after the presence of certain group entities or starting a vehicle when the owner and his driver license on the scene. Most of RFID grouping proof schemes are designed based on symmetric-key cryptography. However, the significant disadvantage of symmetric-key cryptosystem is the key distribution problem that needs all parties to have shared the same key in a secure and authenticated channel before the secure communication happening. The key management is also a great challenge to symmetric-key cryptosystem. In 1976, Diffie and Hellman [2] introduced the fundamental public-key cryptography. In the public-key cryptosystem, the key is split into a public key and a private key, many parties can encrypt message with the receiver’s public key, and the encrypted message only can be decrypted by the receiver with her or his private key. In addition, one party can sign a message with her or his private key and send to many message signature receivers who can verify the signature with the sender’s public key. Therefore, the key management of public-key cryptosystem is easier than symmetric-key cryptosystem.
In 2007, Vaudenay [3] have proven that public-key cryptography can assure the highest level of feasible privacy in RFID applications. Up to now, there are major classes to construct the public-key cryptosystem, which are all based on a mathematical problem that is hard to solve, such as RSA based on large Integer Factorization Problem (IFP), the Diffie-Hellman and ElGamal based on the Discrete Logarithm Problem (DLP), and the Elliptic Curve Cryptosystem (ECC) based on the Elliptic Curve Discrete Logarithm Problem (ECDLP). Among these hard mathematical problems, there are subexponential algorithms for IFP and DLP. In the end of 1980s, Koblitz [4] and Miller [5] independently proposed using the group of points on an elliptic curve defined over a finite field in discrete logarithm cryptosystem. The advantage of ECDLP is that there is absent a subexponential algorithm [6] that could find discrete logarithm in these groups, provided that the curve and the finite field are suitably chosen. Hence, the ECDLP can be regarded as one of the hardest mathematical problem among these public-key cryptosystems. Therefore, the key length for similar level of security in ECC is far less than those public-key cryptosystems based on the IFP and DLP. Consequently, ECC increasingly becomes one of the most popular public-key cryptosystem and is used widely in constrained environment.
Recently in [7,8], ECC was proved to be suitable for RFID applications. In 2010, Batina et al. [9] first proposed a privacy-preserving grouping-proof RFID protocol based on ECC. The protocol allows a pair of RFID tags to prove that they have been scanned simultaneously. But in 2011, Lv et al. [10] proved the protocol in [9] that failed to resist the tracking attack and lost the untraceability. In an RFID system, the untraceability of a protocol means that an attacker cannot distinguish, based on protocol messages, whether two actions were performed by the same tag or by two different tags [11]. Attacking the untraceability of an RFID system, the attacker is trying to figure out that two (or more) seemingly unrelated interactions were with the same tag [12]. In the same article, Lv et al. [10] proposed an intensive protocol to fix the problem. Unfortunately, we found that Lv et al.’s protocol [10] had a defect that caused the protocol to execute improperly. In this paper, at first we review two privacy-preserving grouping proof protocols of [9] and [10]. The vulnerability of Batina et al. [9] will be discussed in detail. And we demonstrate the defect that we found in Lv et al.’s protocol [10]. Furthermore, we propose a new protocol with some nonce to fix the impracticability of Lv et al.’s protocol [10]. We also prove that our protocol can resist the Lv et al.’s tracking attack [10] to possess the untraceability. Therefore our new protocol can concurrently solve the defect of Lv et al.’s protocol [10] and the vulnerability of Batina et al.’s protocol [9].
The rest of this paper is organized as follows. Section 2 introduces the background of ECC. And then, the related works are particularly reviewed in Section 3. In Section 4, we analyze Lv et al.’s protocol and give the proof of the defect in Lv et al.’s protocol [10]. Section 5 gives our new protocol and proves it can resist Lv et al.’s tracing attack [10]. A comparison between protocols of [9,10] and ours are shown in Section 6. Finally, the conclusions and the acknowledgement are given in Section 7 and Section 8 respectively.
2. Background of ECC
This section gives some background of ECC. The addition cyclic subgroup, consisted by the points on an elliptic curve over a finite field, is described and the general form of an elliptic curve is given. Then the ECDLP, the security is relied on in ECC, is mentioned.
2.1. Cyclic Group for ECC
The ECC has a set of points, generated by a primitive point, on the elliptic curve over finite field. These points and the point at infinity, denoted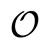 , construct an addition abelian group. Point
, construct an addition abelian group. Point 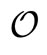 is also said on the curve as an addition identity element of the addition abelian group. Then the ECC is established by taking advantage to the difficult ECDLP in cyclic subgroups of such elliptic curve groups. In the affine plane coordinate system, the elliptic curve equation in general form can be represented as
is also said on the curve as an addition identity element of the addition abelian group. Then the ECC is established by taking advantage to the difficult ECDLP in cyclic subgroups of such elliptic curve groups. In the affine plane coordinate system, the elliptic curve equation in general form can be represented as , known as the affine long Weierstrass equation. Let q be a great prime number, and let Fq denote the finite field of integers modulo q. The equation can be rewritten as its isomorphic curve form
, known as the affine long Weierstrass equation. Let q be a great prime number, and let Fq denote the finite field of integers modulo q. The equation can be rewritten as its isomorphic curve form  by changing variables transforms, where q > 3,
by changing variables transforms, where q > 3, 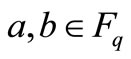 and
and .
.
2.2. ECDLP
The security of ECC is based on the intractability of ECDLP. Given an elliptic curve E, over a finite field Fq, denoted E(Fq). There is a point 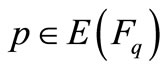 with prime order n. Then P generates the cyclic subgroup,
with prime order n. Then P generates the cyclic subgroup,  , of E(Fq). The public domain parameters are the prime q, the elliptic curve E, the primitive point P and its order n. When given the public domain parameters and a point Q in
, of E(Fq). The public domain parameters are the prime q, the elliptic curve E, the primitive point P and its order n. When given the public domain parameters and a point Q in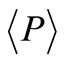 , to find the integer
, to find the integer 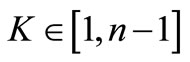 such that Q = kP is an ECDLP. The integer k is the discrete logarithm of Q to the base P, denoted k = logPQ [13].
such that Q = kP is an ECDLP. The integer k is the discrete logarithm of Q to the base P, denoted k = logPQ [13].
3. Related Works
In this section, the notations using throughout in this paper are given. The Batina et al.’s protocol [9], the Lv et al.’s tracing attack [10] on Batina et al.’s work and the protocol proposed by Lv et al. are reviewed in detail.
3.1. Notations
• P: a primitive point of a cyclic subgroup on an elliptic curve defined over a finite field;
• 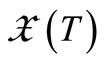 : a function that allows to input an EC point
: a function that allows to input an EC point 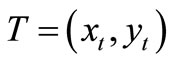 and to return the x-coordinate
and to return the x-coordinate 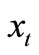 of the point T;
of the point T;
• v: Verifier’s private key;
• V: Verifier’s public key, 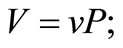
•  : Tag m’s private key;
: Tag m’s private key;
• 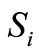 : Tag m’s public key,
: Tag m’s public key, 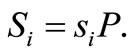
3.2. The Privacy-Preserving ECC-Based Grouping Proof Protocol of Batina et al.
In the Batina et al.’s protocol [9], the tag and/or the reader will abort when a timeout occurs or when they receive the EC (Elliptic Curve) point at infinity. On the basis of public-key cryptography, each tag has its own private key and the public key of verifier before executing the protocol. On the other side, verifier has all tag’s public key in backend database when tags have registered. Then, the details of protocol execution steps are described as follows and shown as Figure 1.
Reader sends the message “start left” to Tag A for assigning the role of tags.
1) Tag A generates a random number ra and computes the corresponding EC point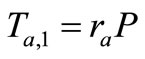 . Then Tag A sends
. Then Tag A sends 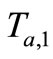 to Reader.
to Reader.
2) Reader generates a random number rs. Then Reader sends “start right”,  and
and 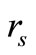 to Tag B.
to Tag B.
3) Tag B generates a random number rb and computes
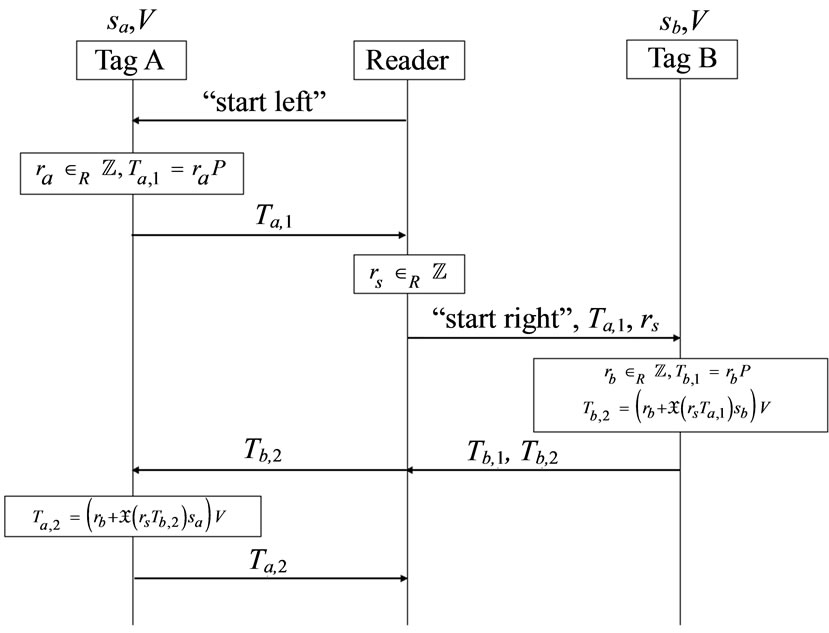
Figure 1. Batian et al.’s grouping-proof protocol [9].
EC points 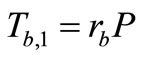 and
and
 .
.
Then Tag B responds 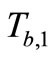 and
and  to Reader.
to Reader.
4) Reader forwards 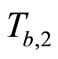 to Tag A. Tag A computes
to Tag A. Tag A computes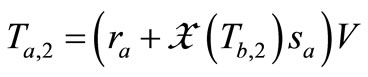 , and sends
, and sends 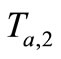 to Reader.
to Reader.
5) Then Reader collects the grouping proof 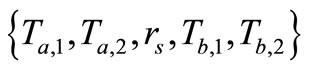 and forwards to Verifier.
and forwards to Verifier.
6) At the last, Verifier verifies
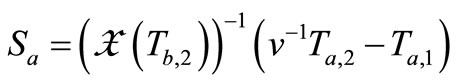
and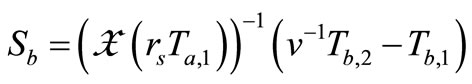 .
.
3.3. Vulnerability of Batina et al.’s Protocol
In 2011, Lv et al. [10] performed the tracking attack on Batina et al.’s grouping-proof protocol [9] in three phases to prove the vulnerability. These three phases are described as follows and shown as Figure 2.
Phase I:
Attacker eavesdrops on the normal messages 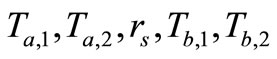 as her or his knowledge.
as her or his knowledge.
Phase II:
Attacker impersonates Reader to challenge Tag B with “start right”, 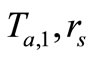 , where
, where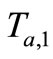 ,
, 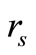 got from Phase I. After receiving the challenge from the fake Reader, Tag B generates a new random number
got from Phase I. After receiving the challenge from the fake Reader, Tag B generates a new random number 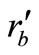 and computes
and computes 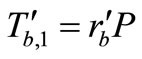 and
and
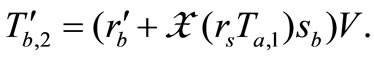
Then, Tag B replies the message 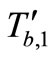 and
and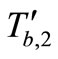 .
.
Phase III:
At the last phase, Attacker listens and waits for next normal session happening. In that case, Reader sends “start left” to Tag A. Then Tag A generates a new random number 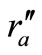 and calculates
and calculates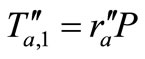 . Tag A replies
. Tag A replies 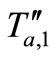 for Reader. Reader generates a new random number
for Reader. Reader generates a new random number 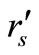 as
as  being received. Then Reader challenges Tag
being received. Then Reader challenges Tag
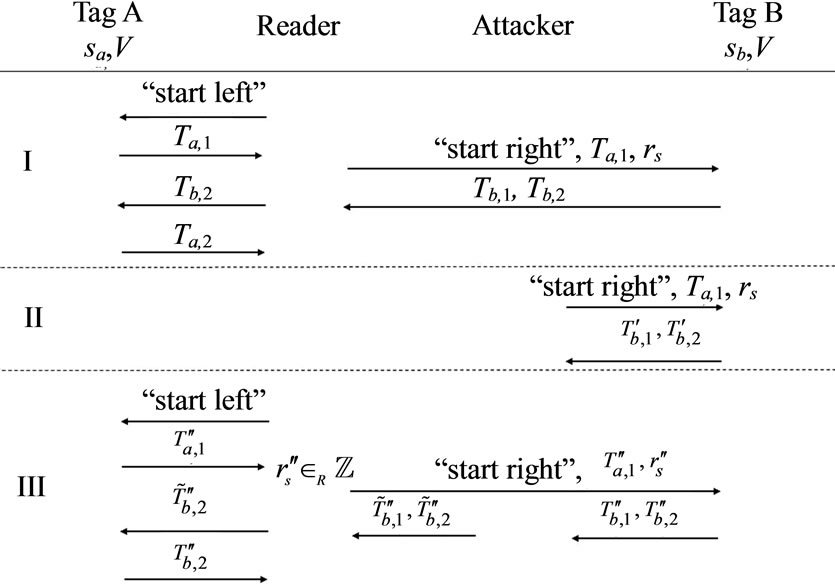
Figure 2. Lv et al.’s tracking attack [10].
B with 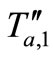 and
and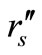 . After the challenge messages arriving, Tag B generates a random number
. After the challenge messages arriving, Tag B generates a random number 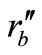 as well as computes
as well as computes  and
and 
Then Tag B replies 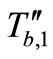 and
and . At this moment, Attacker blocks these messages and forges these messages as
. At this moment, Attacker blocks these messages and forges these messages as
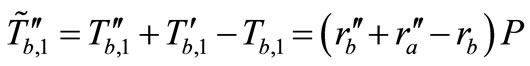
and
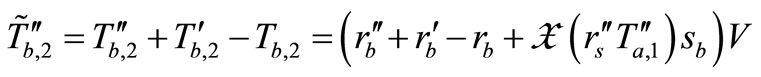 .
.
Then Attacker sends 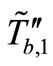 and
and 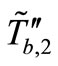 to Reader. And Reader forwards
to Reader. And Reader forwards  to Tag A. Once Tag A received
to Tag A. Once Tag A received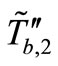 , Tag A computes
, Tag A computes 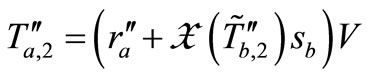 and replies it for Reader. Reader collects grouping proof messages as
and replies it for Reader. Reader collects grouping proof messages as 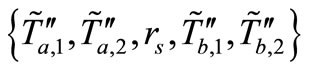 and forwards to Verifier. Then Verifier verifies
and forwards to Verifier. Then Verifier verifies
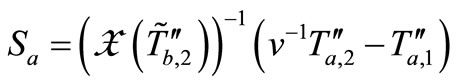
and
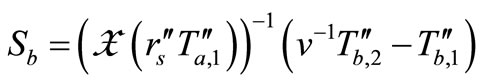
successfully. Thus, Attacker can perform a tracking attack which makes the leakage of tag location in the protocol.
3.4. The Revised Protocol Proposed by Lv et al.
Lv et al.’s proposed a revised protocol [10] to resist tracking attack for Batina et al.’s protocol [9]. The revised protocol is shown in Figure 3 and described as follows.
1) Reader sends the messages “start left” to Tag A.
2) Tag A generates a random number ra and computes the corresponding EC point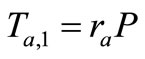 . Then Tag A sends
. Then Tag A sends 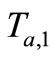 to Reader.
to Reader.
3) Reader generates a random number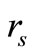 . Then Read-
. Then Read-
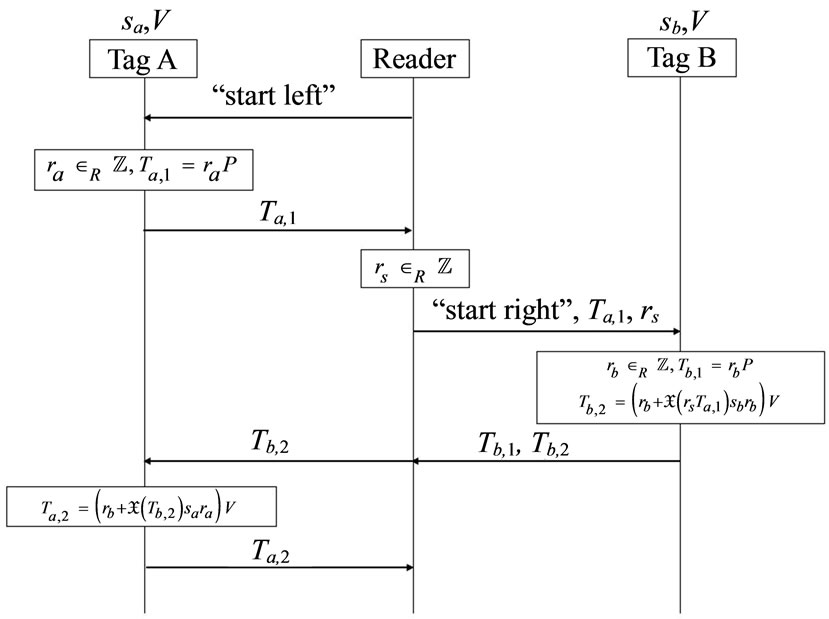
Figure 3. Lv et al.’s revised protocol [10].
er sends “start right”, 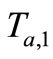 and
and 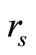 to challenge Tag B.
to challenge Tag B.
4) Tag B generates a random number 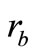 and computes EC points
and computes EC points 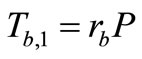 and
and
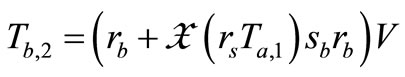 .
.
Then Tag B responds  and
and 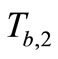 to Reader.
to Reader.
5) Reader forward 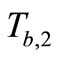 to tag A. Tag A computes
to tag A. Tag A computes 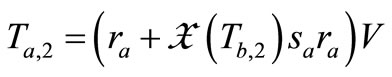 and sends
and sends 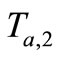 to Reader.
to Reader.
6) Then Reader collects the grouping proof 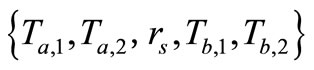 and forwards to Verifier.
and forwards to Verifier.
7) At the last, Verifier verifies
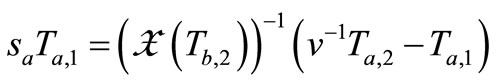
and
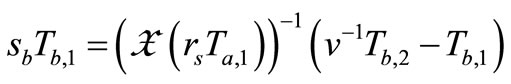 .
.
4. The Impracticability of Lv et al.’s Revised Protocol
Batia et al.’s protocol [9] was designed on the basis of public-key cryptography, therefore public key and private key were involved. Basically, Lv et al.’s protocol [10] was revised from Batia et al.’s protocol [9]. Thus, Lv et al.’s revised protocol [10] should follow the princeple of public-key cryptography. However, we find Lv et al.’s revised protocol [10] has impracticability on the basis of public-key cryptography.
In Lv et al.’s protocol [10], Reader collects the grouping proof 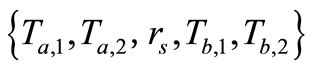 and provides for Verifier to verify. Then in accordance with the step (7) in subsection 3.4, Verifier needs to compute
and provides for Verifier to verify. Then in accordance with the step (7) in subsection 3.4, Verifier needs to compute 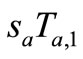 and
and . But based on public-key cryptography, Verifier cannot have tags’ secret keys,
. But based on public-key cryptography, Verifier cannot have tags’ secret keys,  and
and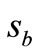 , to execute this verification. In the other case of
, to execute this verification. In the other case of  and
and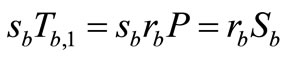 , Verifier can get tags’ public keys,
, Verifier can get tags’ public keys, 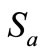 and
and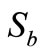 , but cannot get
, but cannot get 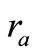 and
and 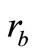 to compute
to compute  and
and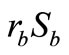 . Consequently, this verification cannot be completed. Obviously, Lv et al.’s protocol [10] is impracticable in the public-key cryptography.
. Consequently, this verification cannot be completed. Obviously, Lv et al.’s protocol [10] is impracticable in the public-key cryptography.
5. Proposed Protocol
In this section, we propose a new protocol to satisfy the functionalities of Batia et al.’s protocol [9] and resist the Lv et al.’s attack model [10]. The new protocol is described step by step in subsection 5.1. Then we analyze the security of the protocol and use Lv et al.’s attack [10] to our protocol to show its resistibility for this kind tracing attack.
5.1. Protocol Description
The proposed protocol is described as the following steps and shown as Figure 4.
1) Reader sends the message “start left” to Tag A.
2) Tag A generates a random number 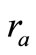 and a nonce
and a nonce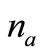 . Then Tag A computes the corresponding EC point
. Then Tag A computes the corresponding EC point 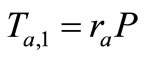 and sends
and sends 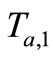 to reader.
to reader.
3) Reader generates a random number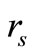 . Then Reader sends “start right”,
. Then Reader sends “start right”,  and
and 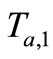 to challenge Tag B.
to challenge Tag B.
4) Tag B generates a random number rb and a nonce nb. Then Tag B computes EC points 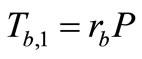 and
and 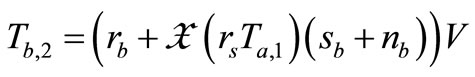 . Then Tag B responds
. Then Tag B responds 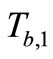 and
and 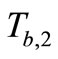 to Reader.
to Reader.
5) Reader forwards 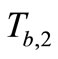 to Tag A. Tag A computes
to Tag A. Tag A computes 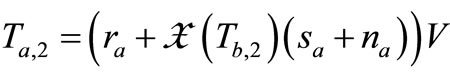 and sends
and sends  to Reader.
to Reader.
6) Then Reader collects the grouping proof 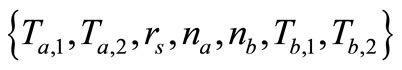 and forwards to Verifier.
and forwards to Verifier.
7) At the last, Verifier verifies
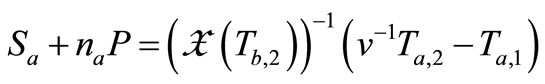
and
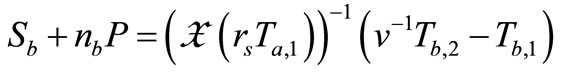 .
.
5.2. Analysis
In this section, we use Lv et al.’s attack [10] on our protocol and prove the protocol can resist this attack. As the tracking attack shown in Figure 2, the attacker eavesdrops on messages ,
, 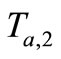 ,
, 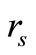 ,
,  ,
, 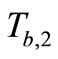 in Phase I. Then the attacker challenges Tag B by sending
in Phase I. Then the attacker challenges Tag B by sending 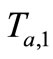 and
and

Figure 4. Proposed protocol.
 . In our protocol, Tag B generates a nonce
. In our protocol, Tag B generates a nonce 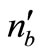 which guarantees every response include a different nonce in
which guarantees every response include a different nonce in
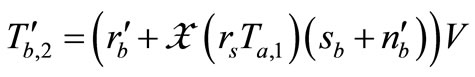 .
.
Then in the Phase III,
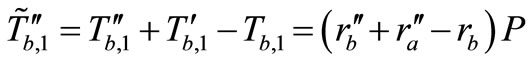
and
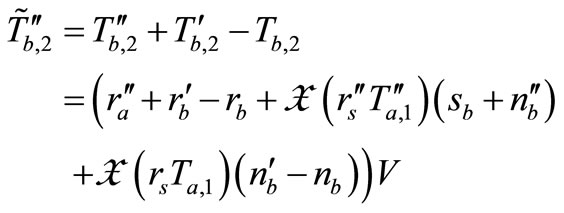
Verifier computes
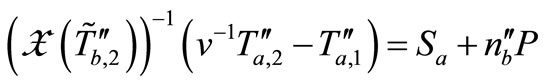
and
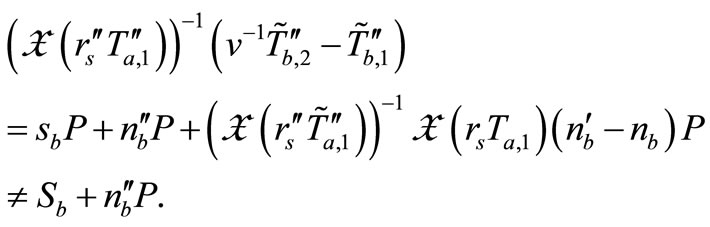
Therefore, the verification is failed. Thus our protocol can resist Lv et al.’s attack [10] and keep all secure properties of Batina et al.’s protocol [9].
6. Comparison with Previous Protocols
In this section we compare our protocol with previous ECC-based privacy-preserving grouping proof protocols as Table 1. At first, our protocol and Batina et al.’s protocol [9] are based on public-key cryptosystem that can avoid key management problem and support those applications which have large number of users. Both our protocol and Lv et al.’s protocol [10] can resist the tracking attack of [10] to possess untraceability, but our protocol is based on public-key cryptosystem that means our protocol has the practicability. To get better privacy security in our protocol, we needed additional two nonce involve in the protocol. In the last column of Table 1, we let MEC, MS and AS denote the scale multiplication of elliptic curve point, scale multiplication and the scale addition separately. The protocol computation overhead is shown in this column. And our protocol is only two more scale addition operations than the other protocols.

Table 1. Comparision between ECC-based privacy-preserving grouping proof protocols.
7. Conclusion
In this paper, we have reviewed related papers those are based on ECC and provided the privacy-preserving grouping proof for RFID applications. Lv et al. [10] successfully attacked on Batina et al.’s protocol [9] in untraceability. And then they proposed revised Batina et al.’s protocol [9] to resist the tracing attack. However, we found that Batina et al.’s protocol [9] was designed on the basis of public-key cryptography, but Lv et al.’s revised protocol [10] cannot execute properly in public-key cryptography. During the execution of the Lv et al.’s protocol [10], Verifier cannot get tags’ public keys to implement their verification. Besides, Verifier can get tags’ public keys, but cannot solve the ECDLP from 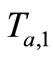 and
and  to get
to get  and
and 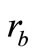 for the verification. Therefore, Lv et al.’s protocol [10] is impractical. To fix this problem, we propose a practical ECC-based privacypreserving grouping proof protocol on the basis of public-key cryptography. We have proved that our protocol can resist the Lv et al.’s tracking attack [10] to complete the untraceability and inherits the security properties of Batina et al.’s protocol [9]. Therefore our new protocol provide the contributions to give the solutions for the defect of Lv et al.’s protocol [10] and the vulnerability of Batina et al.’s protocol [9] simultaneously.
for the verification. Therefore, Lv et al.’s protocol [10] is impractical. To fix this problem, we propose a practical ECC-based privacypreserving grouping proof protocol on the basis of public-key cryptography. We have proved that our protocol can resist the Lv et al.’s tracking attack [10] to complete the untraceability and inherits the security properties of Batina et al.’s protocol [9]. Therefore our new protocol provide the contributions to give the solutions for the defect of Lv et al.’s protocol [10] and the vulnerability of Batina et al.’s protocol [9] simultaneously.
8. Acknowledgements
The authors would like to thank the National Science Council of the Republic of China, Taiwan for financially supporting this research under Contract No. NSC100- 2221-E-182-040.
REFERENCES
- A. Juels, “‘Yoking-Proofs’ for RFID Tags,” Proceedings of the Second IEEE Annual Conference on Pervasive Computing and Communications Workshops, Orlando, 14-17 March 2004, pp. 138-143.
- W. Diffe and M. E. Hellman, “New Directions in Cryptography,” IEEE Transaction on Information Theory, Vol. 22, No. 6, 1976, pp. 644-654. doi:10.1109/TIT.1976.1055638
- S. Vaudenay, “On Privacy Models for RFID,” In: Advances in Cryptology (ASI-ACRYPT’07), Lecture Notes in Computer Science, Vol. 4833, Springer-Verlag, Berlin, 2007, pp. 68-87.
- N. Koblitz, “Elliptic Curve Cryptosystems,” Mathematics of Computation, Vol. 48, 1987, pp. 203-209. doi:10.1090/S0025-5718-1987-0866109-5
- V. Miller, “Use of Elliptic Curves in Cryptography,” In: Advances in Cryptology CRYPTO85, Lecture Notes in Computer Science, Vol. 218, Springer-Verlag, Berlin, 1986, pp. 417-426.
- S. Galbraith, “Mathematics of Public Key Cryptography,” 2011. http://www.math.auckland.ac.nz/~sgal018/crypto-book/crypto-book.html
- J. Wolkerstorfer, “Is Elliptic Curve Cryptography Suitable to Secure RFID Tags?” Workshop on RFID and Lightweight Crypto, Graz, 13-15 July 2005.
- D. Hein, J. Wolkerstorfer and N. Felber, “ECC Is Ready for RFID—A Proof in Silicon,” Lecture Notes in Computer Science, Vol. 5381, 2008, pp. 401-413.
- L. Batina, Y. K. Lee, S. Seys, D. Singelée and I. Verbauwhede, “Short Paper: Privacy Preserving ECC-based Grouping Proofs for RFID,” Lecture Notes in Computer Science, Vol. 6531, 2010, pp. 159-165.
- C. Lv, H. Li, J. Ma, B. Niu and H. Jiang, “Security Analysis of a Privacy-Preserving ECC-Based Grouping-Proof Protocol,” Journal of Convergence Information Technology, Vol. 6 No. 3, 2011, pp. 113-119. doi:10.4156/jcit.vol6.issue3.13
- T. van Deursen, S. Mauw and S. Radomirovic, “Un-Traceability of RFID Protocols,” Lecture Notes in Computer Science, Vol. 5019, 2008, pp. 1-15. doi:10.1007/978-3-540-79966-5_1
- T. van Deursen, “50 Ways to Break RFID Privacy,” IFIP Advances in Information and Communication Technology, Vol. 352, 2011, pp. 192-205. doi:10.1007/978-3-540-79966-5_1
- D. Hankerson, A. Menezes and S. Vanstone, “Guide to Elliptic Curve Cryptography,” Springer-Verlag, Berlin, 2004.
NOTES
*Corresponding author.

