Applied Mathematics
Vol. 3 No. 2 (2012) , Article ID: 17391 , 7 pages DOI:10.4236/am.2012.32023
New Oscillation Results for Forced Second Order Differential Equations with Mixed Nonlinearities
Department of Mathematics, Faculty of Arts and Sciences, Gaziosmanpaşa University, Tokat, Turkey
Email: ercantunc72@yahoo.com, adilkaymaz@gmail.com
Received November 17, 2011; revised December 17, 2011; accepted December 25, 2011
Keywords: Generalized variational principle; variational principle; second order differential equations; Riccati transformation; oscillation
ABSTRACT
Some new oscillation criteria are given for forced second order differential equations with mixed nonlinearities by using the generalized variational principle and Riccati technique. Our results generalize and extend some known oscillation results in the literature.
1. Introduction
The oscillatory behavior of second order differential equations has a major role in the theory of differential equations. It has been shown that many real world problems can be modelled, in particular, by half linear differential equations which can be regarded as a natural generalization of linear differential equations [1- 14]. A considerable amount of research has also been done on quasi-linear [15-18] and nonlinear second order differential equations [19-23].
In this paper, we investigate the oscillatory behavior of second order forced differential equation with mixed nonlinearities.
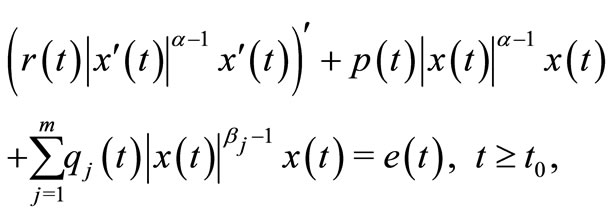 (1)
(1)
where ,
,  and
and  are real numbers,
are real numbers, 
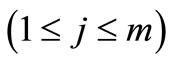 and
and ![]() might alternate signs.
might alternate signs.
By a solution of Equation (1), we mean a function , where
, where 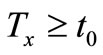 depends on the particular solution, which has the property that
depends on the particular solution, which has the property that 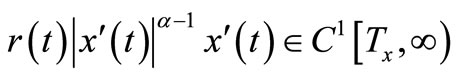 and satisfies Equation (1). We restrict our attention to the nontrivial solutions
and satisfies Equation (1). We restrict our attention to the nontrivial solutions 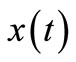 of Equation (1) only, i.e., to solutions
of Equation (1) only, i.e., to solutions  such that
such that 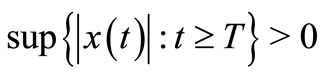 for all
for all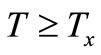 . A nontrivial solution of (1) is oscillatory if it has arbitrarily large zeros, otherwise, it is called non-oscillatory. Equation (1) is said to be oscillatory if all its nontrivial solutions are oscillatory.
. A nontrivial solution of (1) is oscillatory if it has arbitrarily large zeros, otherwise, it is called non-oscillatory. Equation (1) is said to be oscillatory if all its nontrivial solutions are oscillatory.
Equation (1) and its special cases such as the linear differential equation
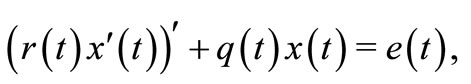 (2)
(2)
the half-linear differential equation
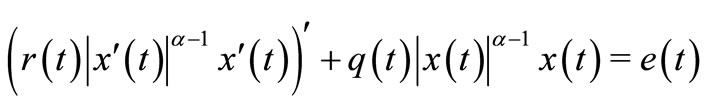 (3)
(3)
and the quasi-linear differential equation
 (4)
(4)
have been extensively studied by numerous authors with different methods (see, for example, [1-5,15-19] and the references quoted therein).
In 1999, Wong [1] proved the following theorem by making use of the “oscillatory intervals” of e(t) and Leighton’s variational principle (see [10]) for (2).
Theorem 1.1. Suppose that for any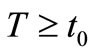 , there exist
, there exist  such that
such that
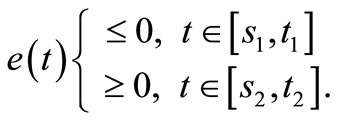 (5)
(5)
Denote

If there exist 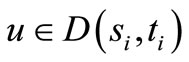 such that
such that
 (6)
(6)
then Equation (2) is oscillatory.
Afterwards, in 2002, the authors of [2] extended Wong’s results, using a similar method, to Equation (3) as follows.
Theorem 1.2. Suppose that for any , there exist
, there exist 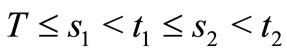 such that (5) holds. Let
such that (5) holds. Let
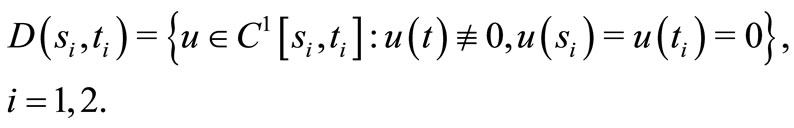
If there exist  and a positive, nondecreasing function
and a positive, nondecreasing function 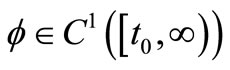 such that
such that
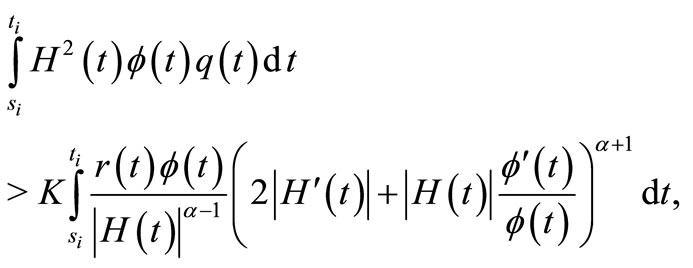 (7)
(7)
for i = 1, 2, where , then (3) is oscillatory.
, then (3) is oscillatory.
Later, in 2007, Zheng and Meng [16], considering a more general equation (4), improved the paper [2] and showed that the results obtained in [2] for Equation (3) can not be applied to the case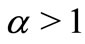 . The main result of Zheng and Meng [16] is the following.
. The main result of Zheng and Meng [16] is the following.
Theorem 1.3. Assume that for any , there exist
, there exist  such that (5) holds. Let
such that (5) holds. Let
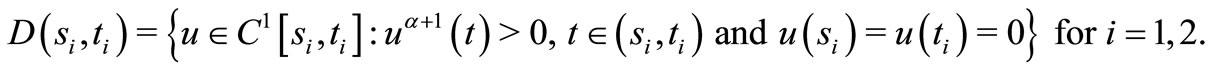
Suppose that there exist 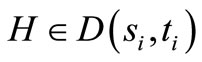 and a positive, nondecreasing function
and a positive, nondecreasing function 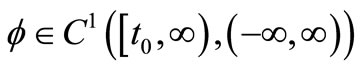 such that
such that
 (8)
(8)
for i =1, 2. Then Equation (4) is oscillatory, where
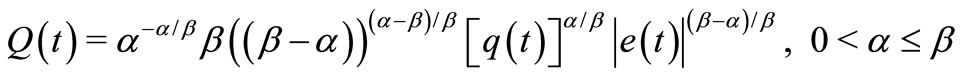 (9)
(9)
with the convention that 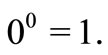
Also, in [2009], Zheng et al. [17] extended the results obtained for Equation (4) to Equation (1) as follows.
Theorem 1.4. Assume that for any , there exist
, there exist  such that
such that 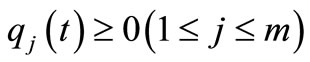 for
for 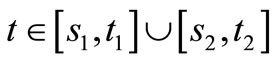 and (5) holds. Let
and (5) holds. Let
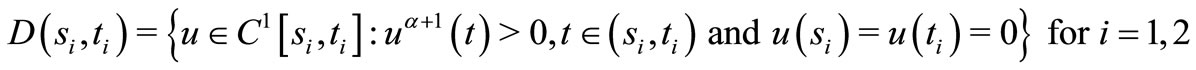 .
.
If there exist  and a positive function
and a positive function  such that
such that
 (10)
(10)
for i = 1, 2. Then Equation (1) is oscillatory, where
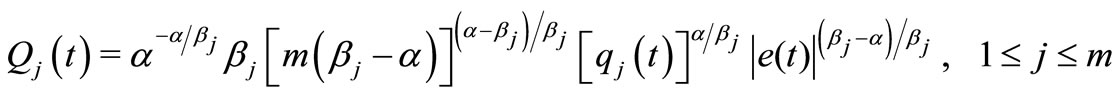 (11)
(11)
with the convention that 
Recently, Shao [15] generalized the results of Zheng and Meng [16] by using the generalized variational principle due to Komkov [24] and gave the following result for Equation (4).
Theorem 1.5. Assume that, for any , there exist
, there exist 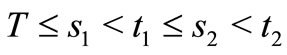 such that (1.5) holds. Let
such that (1.5) holds. Let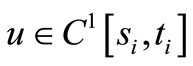 , and nonnegative functions
, and nonnegative functions  satisfying
satisfying 
 are continuous and
are continuous and 
for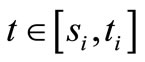 , i = 1, 2. If there exists a positive function
, i = 1, 2. If there exists a positive function 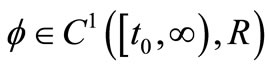 such that
such that
 (12)
(12)
for i = 1, 2, then Equation (4) is oscillatory, where 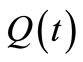 is the same as (9).
is the same as (9).
Motivated by the above theorems we propose some new oscillation results by employing the generalized variational principle and Riccati technique for Equation (1). Our results extend and generalize some known results in the literature. We now state our main results and several remarks.
2. New Oscillation Results
In order to prove our results we use the following wellknown inequality which is presented by Hardy et al. [25].
Lemma 2.1. (see [25]). If 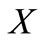 and
and ![]() are nonnegative, then
are nonnegative, then
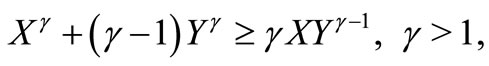 (13)
(13)
where equality holds if and only if 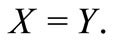
Theorem 2.1. Assume that, for any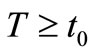 , there exist
, there exist 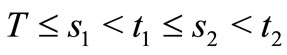 such that
such that
 for
for  and (5)
and (5)
holds. Let 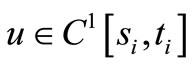 and nonnegative functions
and nonnegative functions
 satisfying
satisfying
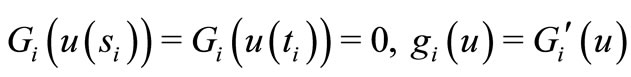
are continuous and
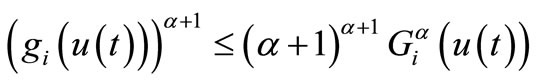
for , i = 1, 2. If there exists a positive function
, i = 1, 2. If there exists a positive function 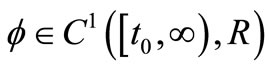 such that
such that
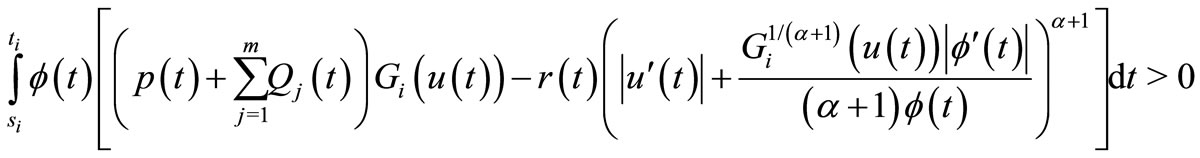 (14)
(14)
for i =1, 2, then Equation (1) is oscillatory, where  is the same as (11).
is the same as (11).
Proof. Suppose that  is a nonoscillatory solution of Equation (1). Then, there exists a
is a nonoscillatory solution of Equation (1). Then, there exists a  such that
such that 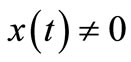 for all
for all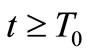 . Without loss of generality, we may assume that
. Without loss of generality, we may assume that 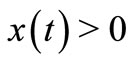 for all
for all
 . We introduce the Ricccati transformation
. We introduce the Ricccati transformation
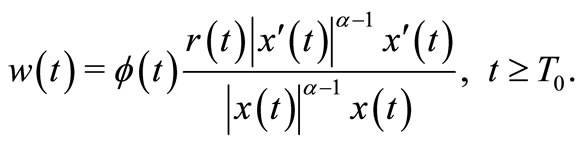 (15)
(15)
Differentiating (15) and using (1), we obtain, for all ,
,
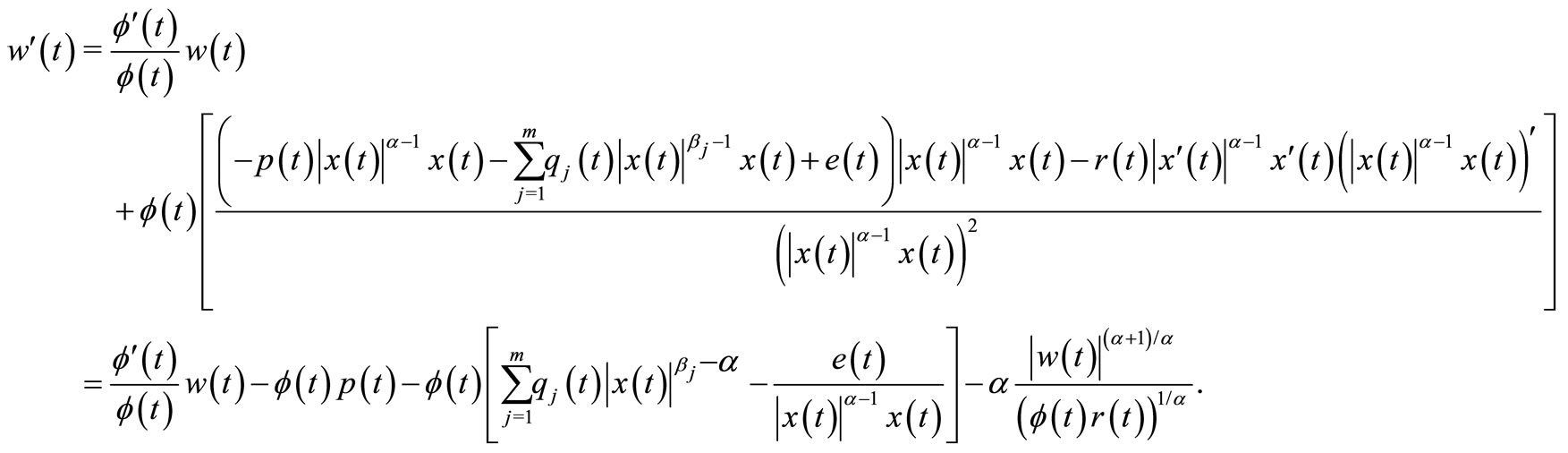 (16)
(16)
By the assumption, we can choose  so that
so that  on the interval
on the interval 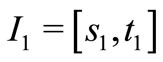 with
with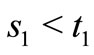 . As in [18], for given
. As in [18], for given , set
, set

It is easy to verify that

So  obtains its minimum on
obtains its minimum on 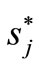 and
and
 (17)
(17)
Then, by using (17) in (16), we get
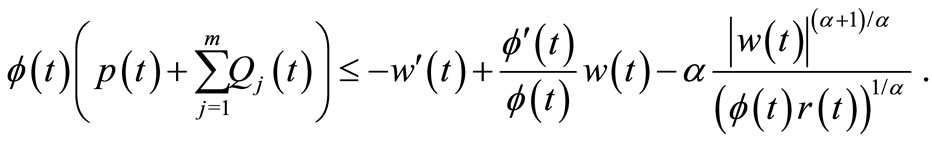 (18)
(18)
Multiplying 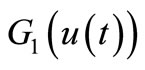 through (18) and integrating over
through (18) and integrating over![]() , we have
, we have
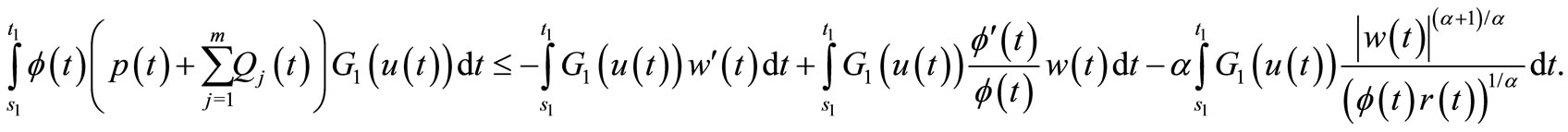 (19)
(19)
By integration by parts and using the fact that 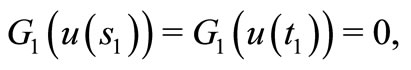 we have
we have
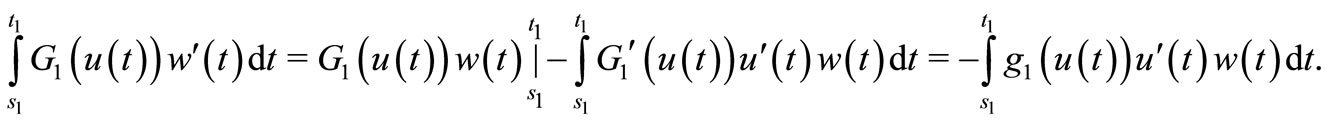 (20)
(20)
In view of (19) and (20), we conclude that
 (21)
(21)
Let
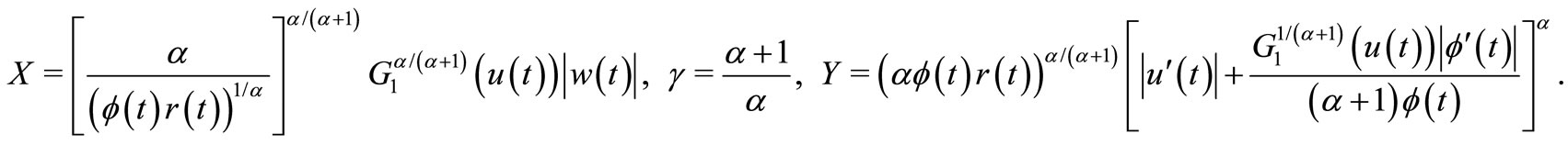
According to Lemma 2.1, we obtain for 
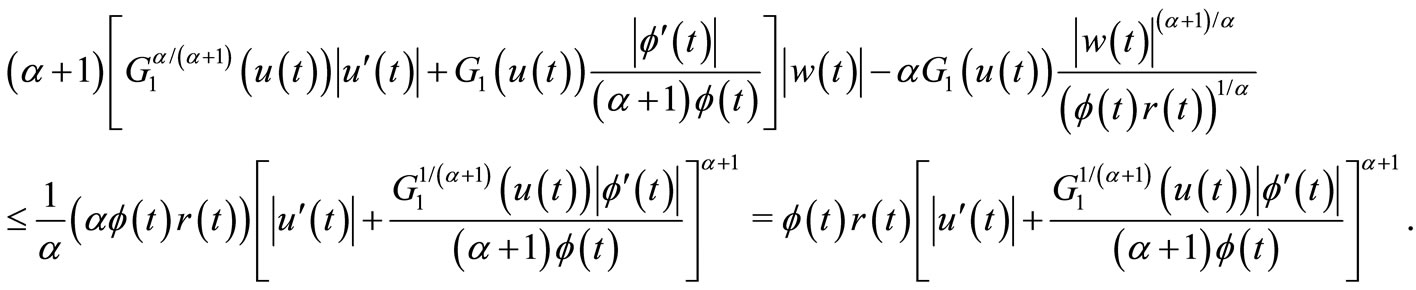
Therefore, (21) yields

which contradicts the assumption (14) for .
.
When  is a negative solution for
is a negative solution for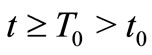 , we may employ the fact that
, we may employ the fact that  on
on 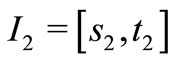 to reach a similar contradiction. Therefore, any solution
to reach a similar contradiction. Therefore, any solution 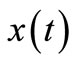 can be neither eventually positive nor eventually negative. Hence, any solution is oscillatory. This completes the proof of Theorem 2.1.
can be neither eventually positive nor eventually negative. Hence, any solution is oscillatory. This completes the proof of Theorem 2.1.
If 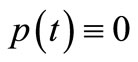 and
and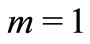 , then Equation (1) reduces to Equation (4). Thus by Theorem 2.1, we have the following oscillation result:
, then Equation (1) reduces to Equation (4). Thus by Theorem 2.1, we have the following oscillation result:
Corollary 2.1. Assume that, for any , there exist
, there exist 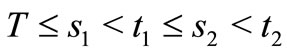 such that (5) holds. Let
such that (5) holds. Let
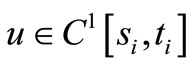 , and nonnegative functions
, and nonnegative functions  satisfying
satisfying 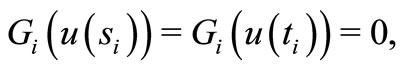
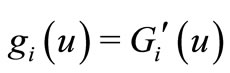 are continuous and
are continuous and 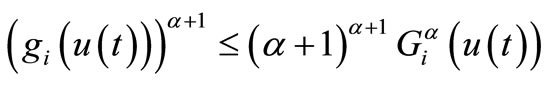
for  for i =1, 2. If there exists a positive function
for i =1, 2. If there exists a positive function  such that
such that
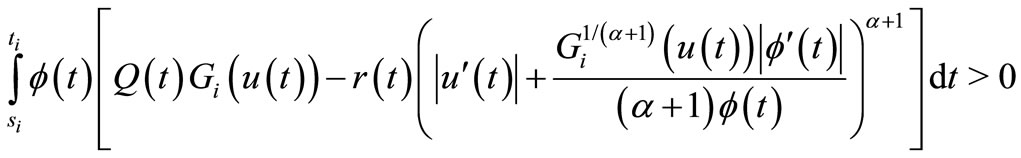 (22)
(22)
for i = 1, 2, then Equation (4) is oscillatory, where 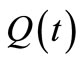 is the same as (9).
is the same as (9).
Remark 1. Corollary 2.1 shows that Theorem 2.1 is a generalization of Theorem 1.5.
Remark 2. Let 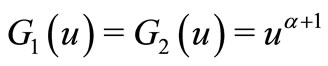 in Corollary 2.1, then our main Theorem 2.1 reduces to Theorem 1.3.
in Corollary 2.1, then our main Theorem 2.1 reduces to Theorem 1.3.
Remark 3. If we choose  in Theorem 2.1, then we obtain Theorem 1.4.
in Theorem 2.1, then we obtain Theorem 1.4.
Remark 4. If we choose 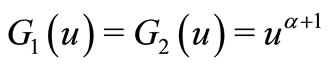 and
and 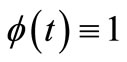 in Theorem 2.1, then we obtain Corollary 2.3 of Paper [17].
in Theorem 2.1, then we obtain Corollary 2.3 of Paper [17].
Remark 5. If we choose  and
and 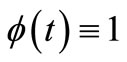 in Corollary 2.1, then we obtain Corollary 2.3 of paper [16].
in Corollary 2.1, then we obtain Corollary 2.3 of paper [16].
Remark 6. Let
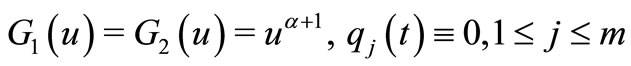
and  in Theorem 2.1, then Theorem 2.1 is a generalization of Theorem 1.1.
in Theorem 2.1, then Theorem 2.1 is a generalization of Theorem 1.1.
Remark 7. Let 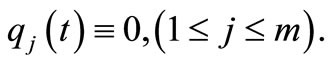 If we choose
If we choose 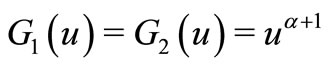 in Theorem 2.1, then Theorem 2.1 improves Theorem 1.2, since the positive constant
in Theorem 2.1, then Theorem 2.1 improves Theorem 1.2, since the positive constant ![]() in Theorem 2.1 can be chosen as any number lying in
in Theorem 2.1 can be chosen as any number lying in .
.
Remark 8. If the condition (5) in Theorem 2.1 and Corollary 2.1 is replaced by
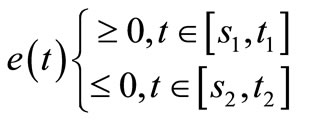
then the results given in this paper are still valid.
3. Examples
Example 3.1. Consider
 (23)
(23)
for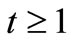 , where
, where 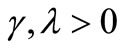 are constants. Let
are constants. Let 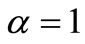
and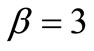 , so
, so . The zeros of forcing term
. The zeros of forcing term 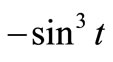 are
are![]() . For any
. For any , we choose
, we choose ![]() sufficiently large so that
sufficiently large so that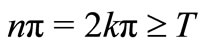 ,
,
 and
and  Letting
Letting 
 (it is easy to verify that
(it is easy to verify that 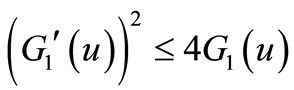 for
for ),
), 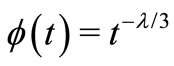 then we obtain
then we obtain

and

Therefore, Equation (14) is satisfied for i = 1 provided that  In a similar way, for
In a similar way, for  and
and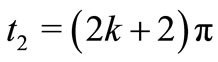 , we choose
, we choose ,
, 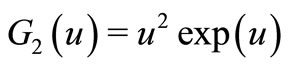 (it is easy to verify that
(it is easy to verify that  for
for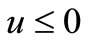 ) so that that (14) is valid for i = 2. Thus (23) is oscillatory for
) so that that (14) is valid for i = 2. Thus (23) is oscillatory for
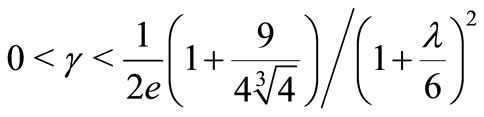
by Theorem 2.1.
Example 3.2. Consider the following forced quasilinear differential equation
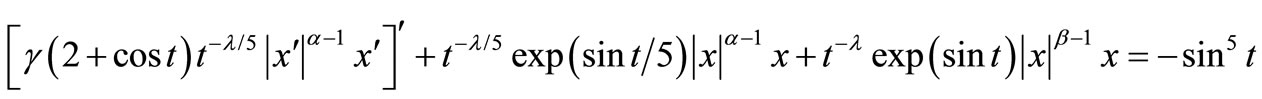 (24)
(24)
for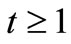 , where
, where  are constants. Let
are constants. Let 
and , so
, so 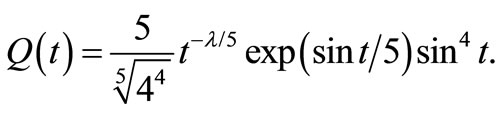 The zeros of forcing term
The zeros of forcing term 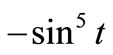 are
are![]() . For any
. For any 
we choose n sufficiently large so that  ,
,  and
and 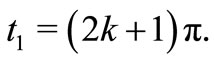 Letting
Letting
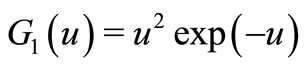
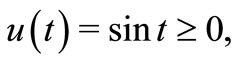 ,
,  then we obtain
then we obtain
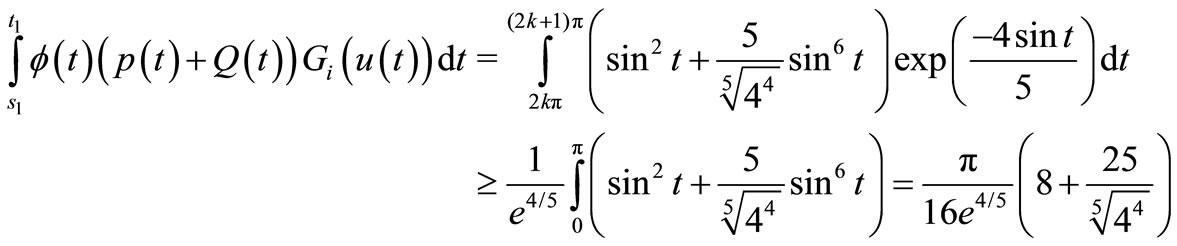
and
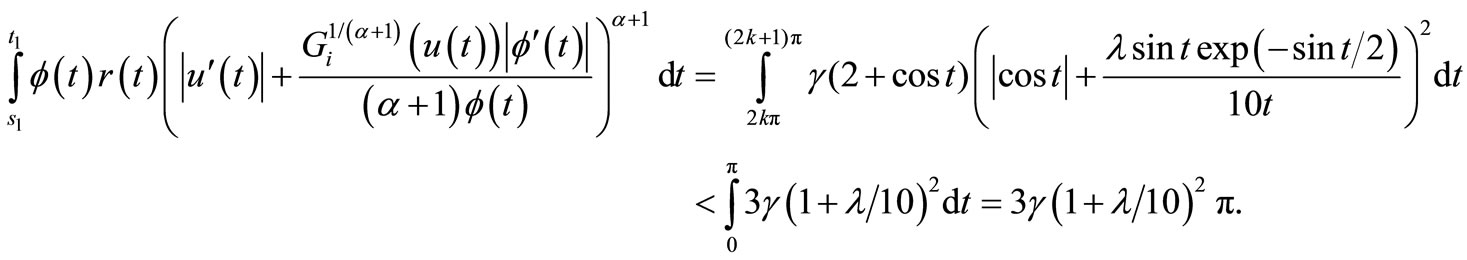
Therefore, Equation (14) is satisfied for i = 1 provided that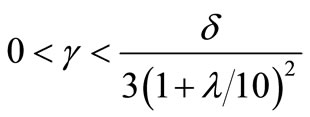 , where
, where 
In a similar way, for  and
and 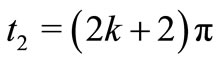 , we choose
, we choose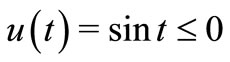 ,
, 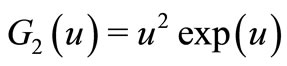 so that (14) is valid for i = 2. Thus (24) is oscillatory for
so that (14) is valid for i = 2. Thus (24) is oscillatory for  by Theorem 2.1.
by Theorem 2.1.
4. Conclusion
The oscillatory behavior of many different kinds of differential equations has been investigated and a great deal of results has been obtained in the literature. In this article, we generalized the results obtained in [16,17] and extended the results of Shao [15] by using the generalized variational principle and Riccati tecnique. In a similar way, the results obtained for Equation (1) can be extended to a more general class of differential equations.
5. Acknowledgements
The authors would like to express sincere thanks to the anonymous referee for her/his invauable corrections, comments and suggestions on the paper.
REFERENCES
- J. S. W. Wong, “Oscillation Criteria for a Forced SecondOrder Linear Differential Equation,” Journal of Mathematical Analysis and Applications, Vol. 231, No. 1, 1999, pp. 235-240. doi:10.1006/jmaa.1998.6259
- W. T. Li and S. S. Cheng, “An Oscillation Criterion for Nonhomogeneous Half-Linear Differential Equations,” Applied Mathematics Letters, Vol. 15, No. 3, 2002, pp. 259-263. doi:10.1016/S0893-9659(01)00127-6
- J. V. Manojlovic, “Oscillation Criteria for Second-Order Half-Linear Differential Equations,” Mathematical and Computer Modelling, Vol. 30, No. 5-6, 1999, pp. 109- 119. doi:10.1016/S0895-7177(99)00151-X
- Q. R. Wang, “Oscillation and Asymptotics for SecondOrder Half-Linear Differential Equations,” Applied Mathematics and Computation, Vol. 122, No. 2, 2001, pp. 253- 266. doi:10.1016/S0096-3003(00)00056-4
- Q. R. Wang and Q. G. Yang “Interval Criteria for Oscillation of Second-Order Half-Linear Differential Equations,” Journal of Mathematical Analysis and Applications, Vol. 291, No. 1, 2004, pp. 224-236. doi:10.1016/j.jmaa.2003.10.028
- J. Jaros and T. Kusano, “A Picone Type Identity for Second Order Half-Linear Differential Equations,” Acta Mathematica Universitatis Comenianae, Vol. 68, No. 1, 1999, pp. 137-151.
- A. Elbert, “A Half-Linear Second Order Differential Equation,” Colloquia Mathematica Societatis Janos Bolyai: Qualitative Theory of Differential Equations, Szeged, 1979, pp. 153-180.
- A. Wintner, “A Criterion of Oscillatory Stability,” Quarterly of Applied Mathematics, Vol. 7, 1949, pp. 115-117.
- I. V. Kamenev, “An Integral Criterion for Oscillation of Linear Differential Equations of Second Order,” Matematicheskie Zametki Vol. 23, No. 2, 1978, pp. 249-251.
- W. Leighton, “Comparison Theorems for Linear Differential Equations of Second Order,” Proceedings of the American Mathematical Society, Vol. 13, 1962, pp. 603- 610. doi:10.1090/S0002-9939-1962-0140759-0
- Q. Kong, “Interval Criteria for Oscillation of SecondOrder Linear Ordinary Differential Equation,” Journal of Mathematical Analysis and Applications, Vol. 229, No. 1, 1999, pp. 258-270. doi:10.1006/jmaa.1998.6159
- H. J. Li and C. C. Yeh, “Sturm Comparison Theorem for Half-Linear Second Order Differential Equations,” Proceedings of the Royal Society of Edinburgh, Vol. A125, 1995, pp. 1193-1240. doi:10.1017/S0308210500030468
- O. Došlý and P. Řehák, “Half-Linear Differential Equations,” North-Holland Mathematics Studies, Vol. 202, Elsevier Science, Amsterdam, 2005.
- R. P. Agarwal, S. R. Grace and D. O’Regan, “Oscillation Theory for Second Order Linear, Half-Linear, Superlinear Dynamic Equations,” Kluver, Dordrecht, 2002.
- J. Shao, “A New Oscillation Criterion for Forced SecondOrder Quasi-Linear Differential Equations,” Discrete Dynamics in Nature and Society, Vol. 2011, Hindawi Publishing Corporation, New York, pp. 1-8.
- Z. Zheng and F. Meng, “Oscillation Criteria for Forced Second Order Quasi-Linear Differential Equations,” Mathematical and Computer Modelling, Vol. 45, No. 1-2, 2007, pp. 215-220. doi:10.1016/j.mcm.2006.05.005
- Z. Zheng, X. Wang and H. Han, “Oscillation Criteria for Forced Second Order Differential Equations with Mixed Nonlinearities,” Applied Mathematics Letters, Vol. 22, No. 7, 2009, pp. 1096-1101. doi:10.1016/j.aml.2009.01.018
- J. Jaros, T. Kusano and N. Yoshida, “Generalized Picone’s Formula and Forced Oscillation in Quasi-Linear Differential Equations of the Second Order,” Archivum Mathematicum, Vol. 38, No. 1, 2002, pp. 53-59.
- J. Shao and F. Meng, “Generalized Variational Principles on Oscillation for Nonlinear Nonhomogeneous Differential Equations,” Abstract and Applied Analysis, Vol. 2011, 2011, pp. 1-10.
- Q. Yang, “Interval Oscillation Criteria for a Forced Second Order Nonlinear Ordinary Differential Equations with Oscillatory Potential,” Applied Mathematics and Computation, Vol. 135, No. 1, 2003, pp. 49-64.
- D. Çakmak and A. Tiryaki, “Oscillation Criteria for Certain Forced Second-Order Nonlinear Differential Equations,” Applied Mathematics Letters, Vol. 17, No. 3, 2004, pp. 275-279. doi:10.1016/S0893-9659(04)90063-8
- E. Tunç, “A Note on the Oscillation of Second-Order Differential Equations with Damping,” Journal of Computational Analysis and Applications, Vol. 12, No. 2, 2010, pp. 444-453.
- E. Tunç, “Interval Oscillation Criteria for Certain Forced Second-Order Differential Equations,” Carpathian Journal of Mathematics, Vol. 28, No. 1, 2012, in Press.
- V. Komkov, “A Generalization of Leighton’s Variational Theorem,” Applicable Analysis: An International Journal, Vol. 2, No. 4, 1972, pp. 377-383. doi:10.1080/00036817208839051
- G. H. Hardy, J. E. Littlewood and G. Polya, “Inequalities,” 2nd Edition, Cambridge University Press, Cambridge, 1988.

