Applied Mathematics
Vol. 3 No. 5 (2012) , Article ID: 19053 , 6 pages DOI:10.4236/am.2012.35066
A Casson Fluid Model for Multiple Stenosed Artery in the Presence of Magnetic Field
Department of Mathematics, Harcourt Butler Technological Institute, Kanpur, India
Email: {dr.rekhabali, usha_hbti}@rediffmail.com
Received September 16, 2011; revised March 26, 2012; accepted April 3, 2012
Keywords: Blood Flow; Magnetic Effect; Multiple Stenosis Artery; Casson Fluid
ABSTRACT
The flow of blood through a multistenosed artery under the influence of external applied magnetic field is studied. The artery is modeled as a circular tube. The effect of non-Newtonian nature of blood in small blood vessels has been taken into account by modeling blood as a Casson fluid. The effect of magnetic field, height of stenosis, parameter determining the shape of the stenosis on velocity field, volumetric flow rate in stenotic region and wall shear stress at surface of stenosis are obtained and shown graphically. Some important observations regarding the flow of blood in multi stenosed artery are obtained leading to medical interest.
1. Introduction
Stenosis narrowing of body passage tube or orifice [1] can cause series circulatory disorders by reducing or occluding the blood supply. Stenosis in the arteries supplying blood to the brain can cause cerebral strokes, and in coronary arteries, myocardial infarction, leading to the heart failure. The actual causes of the stenosis are not known, but it has been suggested that cholesterol deposition in arterial wall and profiliferation of connective tissues may be responsible [2], vascular fluid dynamics is reported to play a significant role in the development and progression of the pathological conditions [3].
Blood is suspension of cells in plasma. Due to the presence of hemoglobin (an iron compound) in red cells, blood can be regarded as a suspension of magnetic particle (red cells) in non-magnetic plasma. The effect of a magnetic field on blood flow has been analyzed theoretically by treating blood as an electrically conductive fluid [4]. The conductive flow in the presence of a magnetic field induces voltage and currents, resulting in a decrease in the flow. The importance of heat transfer on artery diseases and blood flow was mentioned by several researcher. Ugulu and Abby [5] claimed that, the heat transfer and a magnetic field have a significant effect on blood flow through constricted artery.
An analytical solution for the steady flow of a viscous fluid through an arbitrary shaped tube of variable crosssection has been presented by Manton [6] using the ideas of steady lubrication theory. Ramachandra Rao and Devanathan [7] and Hall [8] have extended the results of Manton [6] for unsteady pulsatile flows. The steady and unsteady flow through channels and tubes of variable cross-section have been studied by Smith [9] and Duck [10]. Mathematical model for analyzing pulsatile flow in a single stenosed vessels have been proposed by Padmanabhan [11], Mehrotha et al. [12] and Mishra and Chakravorty [13].
The studies on the blood flow/unsteady blood flow through an artery with mild stenosis [14,15] ,effect of arterial dispensability on blood flow through model of mild axi-symmetric arterial stenosis [16], flow of micropolar fluid through a tube with a stenosis [17] nonNewtonian aspects of blood flow through stenosed arteries [18], flow of couple stress fluid through stenotic blood vessels [19], pulsatile flow of Casson’s fluid through stenosed tube [20], oscillatory flow of blood in a stenosed artery [21] and in a single constrcted blood vessels [22], effect of erythrocytes on blood flow characteristics in an indented tube [23], effect of an externally applied uniform magnetic field on the blood flow in a single consitricted blood vessel [24] were also reported. In recent paper Manadal et al. [25] developed a two dimension mathematical model to study the effect of externally imposed periodic body acceleration on nonNewtonian blood flow through an elastic stenosed artery where the blood is characterized by the generalized power-law model.
In all the above studies none has applied magnetic field. But the application of magneto hydrodynamics principles in medicine and biology is of growing interest in the literature of bio-mathematics [26-28]. By Lenz’s law, the Lorentz’s force will oppose the motion of conducting fluid. Since blood is an electrically conducting fluid, The MHD principles may be used to deaccelerate the flow of blood in a human arterial system and thereby it is useful in the treatment of certain cardiovascular disorders and in the diseases which accelerate blood circulation like hemorrhages and hypertension etc. [29].
Our object in the present work is to study the effect of an externally applied uniform magnetic field on the multi-stenosed artery with core region. Blood is modeled as a Casson fluid by properly accounting for yield stress of blood in small blood vessel. The analytical expressions for the velocities (normal and core region), blood flow rate and wall shear stress are obtained. The effect of external magnetic field and other parameter has been shown graphically in these results.
2. Mathematical Formulation
Let us consider the Casson fluid motion of blood through a multi-stenosed artery under the influence of an external applied uniform transverse magnetic fluid. The geometry of the stenosis is as shown in Figure 1. We have taken some assumption for solving the model.
1) Let us take the flow of blood as axially symmetric and fully developed (i.e. , flow in z-direction only). This is entirely reasonable and reinforces the fact that in steady-state incompressible flow in a circular tube of uniform cross-section. The velocity does not change in the direction of the flow, except near the entrance and exist regions.
, flow in z-direction only). This is entirely reasonable and reinforces the fact that in steady-state incompressible flow in a circular tube of uniform cross-section. The velocity does not change in the direction of the flow, except near the entrance and exist regions.
2) Consider blood as a Casson fluid (non-Newtonian) and magnetic fluid. Since red cell is a major biomagnetic substance and blood flow may be influenced by the magnetic field.
3) Consider the transverse magnetic field. Since the biomagnetic fluid (blood) is subjected to a magnetic field, the action of magnetization will introduce a rotational motion to orient the magnetic fluid particle with the magnetic field).
The above assumptions for Navier-Stokes equation is given by (1)

Figure 1. Geometry of multiple stenosed artery.
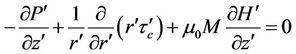 (1)
(1)
where 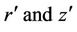 denote the radial and axial coordinates respectively,
denote the radial and axial coordinates respectively,  magnetic permeability, M magnetization,
magnetic permeability, M magnetization, 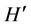 magnetic field intensity,
magnetic field intensity, 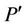 pressure and
pressure and 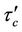 the shear stress. For Casson fluid the relation between shear stress and shear rate is given by Fung [30],
the shear stress. For Casson fluid the relation between shear stress and shear rate is given by Fung [30],
 (2)
(2)
where 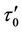 denotes yields stress and
denotes yields stress and 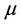 the viscosity of blood.
the viscosity of blood.
The boundary conditions appropriate to the problem under study are
1) (3a)
(3a)
2) 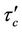 is finite at
is finite at 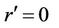 (3b)
(3b)
3) In core region  at
at 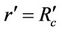 (3c)
(3c)
Here 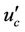 is core velocity.
is core velocity.
3. Solution of the Problem
Introducing the following non-dimensional scheme.
 (4)
(4)
where  is external transverse uniform constant magnetic field.
is external transverse uniform constant magnetic field.
Using the non-dimensional scheme the governing equations from (1)-(3) are written as:
 (5)
(5)
 (6)
(6)
where 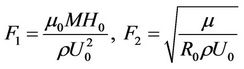
The boundary conditions (3a), (3b), (3c) reduce
1) (7a)
(7a)
2)  is finite at
is finite at 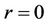 (7b)
(7b)
3) In core region  at
at 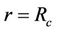 (7c)
(7c)
The geometry of the stenosis in non-dimensional form is given as
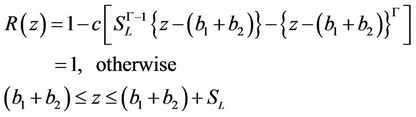 (8)
(8)
where
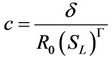 (9)
(9)
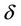 is maximum height of stenosis
is maximum height of stenosis
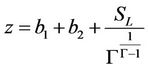 (10)
(10)
where S (≥2) is the parameter for determining the shape of the stenosis.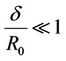 .
.
Solution
On using analytical method in Equations (5)-(7) and using boundary conditions (7a), (7b), (7c) and (8) the expression for velocity u and core velocity  are:
are:
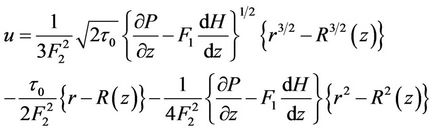 (11)
(11)
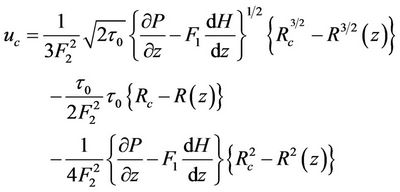 (12)
(12)
The volumetric flow rate Q is given by:
 (13)
(13)
where 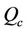 and
and 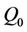 are the flow rate in core and annular region of stenotic tube.
are the flow rate in core and annular region of stenotic tube.
Using the Equations (11) and (12) in Equation (13) then, flow rate Q is:
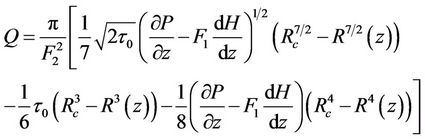 (14)
(14)
The wall shear stress 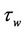 is defined as:
is defined as:
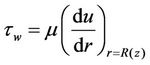 (15)
(15)
On differentiating Equation (11) with respect to r and substituting in Equation (14), then  is given by:
is given by:
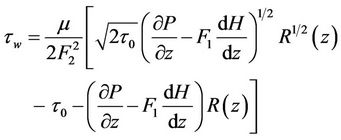 (16)
(16)
4. Results and Discussions
In Figures 2(a) shows the axial velocity (u) with radial axis (r) for different values of induced magnetic field gradient (H = ), when the magnetic field gradient (H =
), when the magnetic field gradient (H =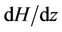 ) increases then the curve shifts towards the origin. This is due to the fact that as magnetic field applied on the body, the Laurentz force oppose the flow of blood and hence reduces its velocity. This result compare with Das [29] and Ponalagusamy [31].
) increases then the curve shifts towards the origin. This is due to the fact that as magnetic field applied on the body, the Laurentz force oppose the flow of blood and hence reduces its velocity. This result compare with Das [29] and Ponalagusamy [31].
In Figure 2(b) the variation of velocity (u) with radial axis (r) for different values of ratio of the maximum height of stenosis and radius of the normal tube 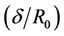 is shown in Figure 2(b). Velocity decreases and it approaches zero when the ratio of the maximum height of stenosis and radius of the normal tube
is shown in Figure 2(b). Velocity decreases and it approaches zero when the ratio of the maximum height of stenosis and radius of the normal tube  increased. Where high shearing velocity produced in order to attain uniform flow rate at given parameter, so the severity of the multi-stenosis affects the axial flow distribution significantly. This result agrees qualitively with Sanyal et al. [32] and Biswas et al. [33].
increased. Where high shearing velocity produced in order to attain uniform flow rate at given parameter, so the severity of the multi-stenosis affects the axial flow distribution significantly. This result agrees qualitively with Sanyal et al. [32] and Biswas et al. [33].
Figure 3, illustrate the variation of core (plug) velocity (uc) with ratio of the stenosis height and radius of the normal tube 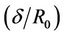 for different values of induced magnetic gradient
for different values of induced magnetic gradient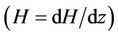 . The curves are all featured to be analogous in the sense that they do drop to zero on the wall surface from their maximum stenosis height
. The curves are all featured to be analogous in the sense that they do drop to zero on the wall surface from their maximum stenosis height . The core velocity decreases with increasing the magnetic gradient
. The core velocity decreases with increasing the magnetic gradient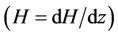 . This observation is in good agreement with those of Tzirtzilakis [34] although his studies were based on the Newtonian blood flow under the action of an applied magnetic field.
. This observation is in good agreement with those of Tzirtzilakis [34] although his studies were based on the Newtonian blood flow under the action of an applied magnetic field.
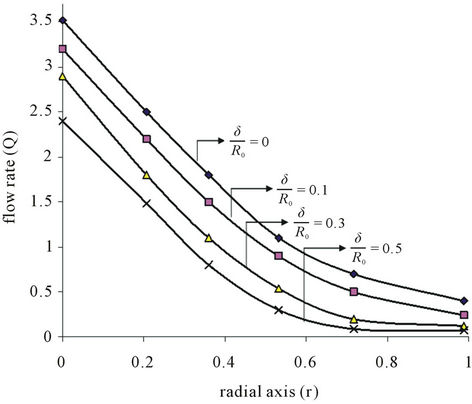
From Figure 4(a), it is clear that the ratio of the stenosis height and radius of the normal tube 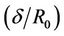 increases the rate of flow diminishes appreciably for radial axis (r). The characterization of blood irrespective of the presence and absence of the magnetic field certainly ensures the importance of blood rheology in the flow phenomena. The flow rate diminishes as the artery gets narrowed gradually. It may be noted further that the flow rate drops sharply with increasing severity of the constriction in the absence of the magnetic field.
increases the rate of flow diminishes appreciably for radial axis (r). The characterization of blood irrespective of the presence and absence of the magnetic field certainly ensures the importance of blood rheology in the flow phenomena. The flow rate diminishes as the artery gets narrowed gradually. It may be noted further that the flow rate drops sharply with increasing severity of the constriction in the absence of the magnetic field.
In Figure 4(b), it is observed from the figure that in the presence of magnetic field gradient 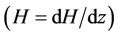
 (a)
(a) (b)
(b)
Figure 2. (a) Variation of velocity (u) with radial axis (r) for different value of magnetic field (H); (b) Variation of velocity (u) with radial axis (r) for different values of stenosis height (δ/R0).

Figure 3. Variation of core velocity (uc) with stenosis height (δ/R0) for different values of magnetic field (H).
 (a)
(a)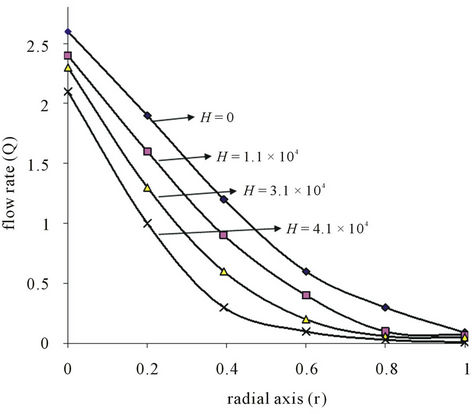 (b)
(b)
Figure 4. (a) Variation of flow rate (Q) with radial axis (r) for different value of stenosis height (δ/R0); (b) Variation of flow rate (Q) with radial axis (r) for different values of magnetic field (H).
the rate of blood flow increases at r = 0 and then diminishes for become the value of (0 < r < 1). The flow rate becomes higher in the absence of magnetic field ant it gradually diminishes with increasing magnetic field gradient  which is in good agreement with these of Haik et al. [35].
which is in good agreement with these of Haik et al. [35].
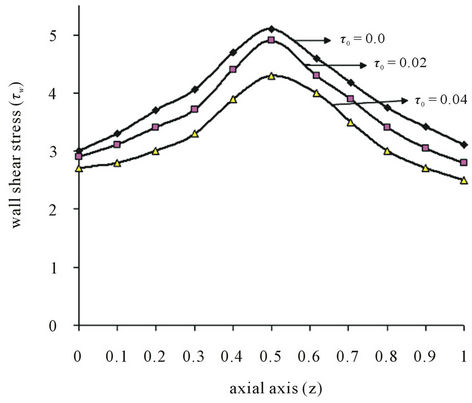
Figure 5(a) shows the result of the varaition of wall shear stress 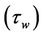 with axial axis (z) for different values of yield stress
with axial axis (z) for different values of yield stress . It is noted that the wall shear stress increases as the axial distance z increases from (0 to 0.5) and then it decreases as z increases from (0.5 to 1). The maximum wall shear stress occurs at the middle of the stenosis. The wall shear stress decreases when the yield stress
. It is noted that the wall shear stress increases as the axial distance z increases from (0 to 0.5) and then it decreases as z increases from (0.5 to 1). The maximum wall shear stress occurs at the middle of the stenosis. The wall shear stress decreases when the yield stress 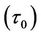 increases. The feature of these results is in
increases. The feature of these results is in
 (a)
(a)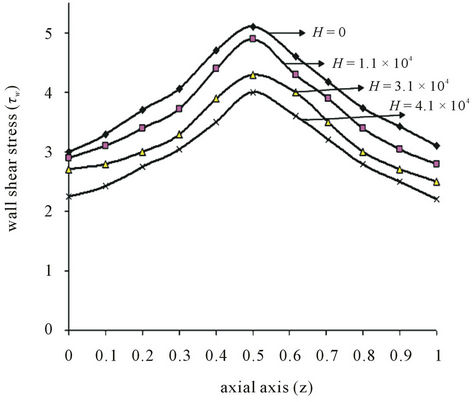 (b)
(b)
Figure 5. (a) Variation of wall shear stress (τw) with axial axis (z) for different values of yield stress (τ0); (b) Variation of wall shear stress (τw) with axial axis (z) for different values of magnetic field (H).
good agreement with that of Srivastava and Saxena [36], whose studies were based on a one-dimensional Casson model of the blood flow in rigid arteries under steadystate conditions in the absence of magnetic field.
Figure 5(b), show the variation of wall shear stress 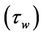 with axial axis (z) for different magnetic field gradient
with axial axis (z) for different magnetic field gradient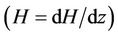 . The wall shear stress increases rapidly as the length of arterial increases z from (0 to 0.5) and gradually decreases for the length of arterial increases z from (0.5 to 1). This is due to large velocity gradient and therefore the severity of the stenosis significantly affects the wall shear stress characteristics. It is also clear from the figure that when magnetic gradient
. The wall shear stress increases rapidly as the length of arterial increases z from (0 to 0.5) and gradually decreases for the length of arterial increases z from (0.5 to 1). This is due to large velocity gradient and therefore the severity of the stenosis significantly affects the wall shear stress characteristics. It is also clear from the figure that when magnetic gradient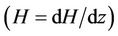 . Increases then the wall shear stress decreases. However as the characteristic of the non-Newtonian fluid changes from shear-thinning to Newtonian. The wall shear stress is observed when the flowing blood is subjected to externally applied transverse magnetic field. The present stress distribution plays an important role in detecting the aggregation sites of platelets as mentioned by Fry [37].
. Increases then the wall shear stress decreases. However as the characteristic of the non-Newtonian fluid changes from shear-thinning to Newtonian. The wall shear stress is observed when the flowing blood is subjected to externally applied transverse magnetic field. The present stress distribution plays an important role in detecting the aggregation sites of platelets as mentioned by Fry [37].
5. Conclusion
From the above discussion, it is clear that the magnetic field, ratio of maximum height of stenosis and radius of normal tube and yield stress of the fluid are the strong parameters influencing the flow. It is observed that, in the presence of magnetic field the magnitude of velocity is decreased. The effect of yield stress and stenosis is to reduce the wall shear stress and flow rate in the presence of magnetic field. In view of these arguments, the present study may be more useful to control the blood flow in diseased state.
6. Acknowledgements
Authors gratefully acknowledge the financial assistance from the UGC major research Project No. 36-320/2008 (SR), for this work first.
REFERENCES
- D. F. Young, “Fluid Mechanics of Arterial Stenosis,” Journal of Biomechanical Engineering, Vol. 101, No. 3, 1979, pp. 157-175. doi:10.1115/1.3426241
- J. B. Shukla, R. S. Parihar and S. P. Gupta, “Effects of Peripheral Layer Viscosity on Blood Flow through the Artery,” Bulletin of Mathematical Biology, Vol. 42, No. 6, 1980, pp. 797-805.
- R. M. Nerem, “Fluid Dynamics Aspects of Arterial Diseases,” Proceedings of a Specialists Meeting, Columbus, 19-20 September 1974.
- I. I. H. Chen, “Analysis of an Intensive Magnetic Field on Blood Flow: Part 2,” Electromagnetic Biology and Medicine, Vol. 4, No. 1, 1985, pp. 55-61. doi:10.3109/15368378509040360
- A. T. Ogulua and T. M. Abbey, “Simulation of Heat Transfer on an Oscillatory Blood Flow in an Indented Porous Artery,” International Communications in Heat and Mass Transfer, Vol. 32, No. 7, 2005, pp. 983-989. doi:10.1016/j.icheatmasstransfer.2004.08.028
- M. J. Manton, “Low Reynolds Number Flow in Slowly Varying Axisymmetric Tubes,” Journal of Fluid Mechanics, Vol. 49, No. 3, 1971, pp. 451-459. doi:10.1017/S0022112071002192
- A. Ramachandra Rao and R. Devanathan, “Pulsatile Flow in Tubes of Varying Cross-Section,” Zeitschrift für Angewandte Mathematik und Physik, Vol. 24, No. 22, 1973, pp. 203-213. doi:10.1007/BF01590913
- P. Hall, “Unsteady Viscous Flow in a Pipe of Slowing Varying Cross-Section,” Journal of Fluid Mechanics, Vol. 64, No. 2, 1974, pp. 209-226. doi:10.1017/S0022112074002369
- F. T. Smith, “Flow through Constricted or Dilated Pipes and Channels: Part-2,” The Quarterly Journal of Mechanics & Applied Mathematics, Vol. 29, No. 3, 1976, pp. 365-376. doi:10.1093/qjmam/29.3.365
- P. W. Duck, “Separation of Jets or Thermal Boundary Layers from a Wall,” Proceedings of the Royal Society A, Vol. 363, No. 2, 1976, p. 33.
- N. Padmanabhan, “Mathematical Model of Arterial Stenosis,” Medical Biological Engineering and Computing, Vol. 18, No. 3, 1980, pp. 281-286. doi:10.1007/BF02443380
- R. Mehrotra, G. Jayaraman and N. Padmanabhan, “Pulsatile Blood Flow in a Stenosed Artery a Theoretical Model,” Medical Biological Engineering and Computing, Vol. 23, No. 1, 1985, pp. 55-62. doi:10.1007/BF02444028
- J. C. Mishra and S. Chakravorty, “Flow in Arteries in the Presence of Stenosis,” Journal of Biomechanics, Vol. 19, No. 11, 1986, pp. 1907-1918.
- J. B. Shukla, R. S. Parihar and B. R. P. Rao, “Effects of Stenosis on Non-Newtonian Flow of the Blood in an Artery,” Bulletin of Mathematical Biology, Vol. 42, No. 3, 1980, pp. 283-294.
- S. Chakravorthy, “Effects of Stenosis on the Flow Behavior of Blood in an Artery,” International Journal of Engineering Science, Vol. 25, No. 8, 1987, pp. 1003-1016. doi:10.1016/0020-7225(87)90093-0
- N. Padmanabhan and R. Devanathan, “Mathematical Model of an Arterial Stenosis, Allowing for Tethering,” Medical Biological Engineering and Computing, Vol. 19, No. 4, 1981, pp. 385-390. doi:10.1007/BF02441299
- R. Devanathan and S. Parvathamma, “Flow of Micropolar Fluid through a Tube with Stenosis,” Medical Biological Engineering and Computing, Vol. 21, No. 4, 1983, pp. 438-445. doi:10.1007/BF02442631
- P. Chaturani and R. P. Swamy, “A Study of Non-Newtonian Aspects of Blood Flow through Stenosed Arteries and Its Applications in Arterial Diseases,” Biorheology, Vol. 22, No. 6, 1985, pp. 512-531.
- L. M. Srivastava, “Flow of Couple Stress Fluid through Stenotic Blood Vessels,” Journal of Biomechanics, Vol. 18, No. 7, 1985, pp. 479-485. doi:10.1016/0021-9290(85)90662-1
- P. Chaturani and R. P. Swamy, “Pulsatile Flow of Casson’s Fluid through Stenosed Arteries with Applications to Blood Flow,” Biorheology, Vol. 23, No. 5, 1986, pp. 499-511.
- K. Haldar, “Oscillatory Flow of Blood in Stenosed Artery,” Bulletin of Mathematical Biology, Vol. 49, No. 3, 1987, pp. 279-287.
- D. C. Sanyal and N. K. Maji, “Unsteady Blood Flow through an Indented Tube with Atherosclerosis,” Indian Journal of Pure and Applied Mathematics, Vol. 30, No. 10, 1999, pp. 951-959.
- K. Haldar and K. N. Dey, “Effect of Erythrocytes on the Flow Characteristic of Blood in an Indented Tube,” Archives of Mechanics, Vol. 42, No. 1, 1990, p. 109.
- K. Haldar and S. N. Ghosh, “Effects of a Magnetic Field on Blood Flow through an Indented Tube in the Presence of Erythrocytes,” Journal of Pure and Applied Mathematics, Vol. 25, No. 3, 1994, pp. 345-352.
- P. K. Mandal, S. Chakravarthy, A. Mandal and N. Amin, “Effect of Body Acceleration on Unsteady Pulsatile Flow of Non-Newtonian Fluid through a Stenosed Artery,” Applied Mathematics and Computation, Vol. 189, No. 1, 2007, pp. 766-779. doi:10.1016/j.amc.2006.11.139
- P. K. Suri and R. Pushpa, “Effect of Static Magnetic Field on Blood Flow in a Branch,” Journal of Pure and Applied Mathematics, Vol. 12, No. 7, 1981, pp. 907-918.
- E. Amos, “Magnetic Effect of Pulsatile Flow in a Constricted Axis Symmetric Tube,” Journal of Pure and Applied Mathematics, Vol. 34, No. 9, 2003, pp. 1315-1326.
- M. A. Elnaby, M. T. N. Eldabe, M. Y. Abou Zied and D. C. Sanyal, “Mathematical Analysis on MHD Pulsatile Flow of a Non-Newtonian Fluid through a Tube with Varying Cross-Section,” Journal of Institute of Mathematics and Computer Science, Vol. 20, No. 1, 2007, pp. 29-42.
- K. Das and G. C. Saha, “Arterial MHD Pulsatile Flow of Blood under Periodic Body Accelaration,” Bulletin of Mathematic Society, Vol. 16, 2009, pp. 21-42.
- Y. C. Fung, “Mechanical Properties of Living Tissue,” Biomechanics, Vol. 4, No. 2, 1986, pp. 68-81.
- R. Ponalagusamy, “Blood Flow through an Artery with Mild Stenosis: A Two-Layered Model Different Shape of Stenoses and Velocity at Wall,” Journal of Applied Sciences, Vol. 7, No. 7, 2007, pp. 1071-1077.
- D. C. Sanyal, K. Das and S. Debnath, “Effect of Magnetic Field on Pulsatile Blood Flow through an Inclined Circular Tube with Periodic Body Acceleration,” Journal of Physical Sciences, Vol. 11, No. 1, 2007, pp. 43-56.
- D. Biswas and U. S. Chakraborty, “Pulsatile Blood Flow through a Catheterized Artery with an Axially Nonsymmetrical Stenosis,” Applied Mathematical Sciences, Vol. 4, No. 58, 2010, pp. 2865-2880.
- E. E. Tzirtzilakis, “A Mathematical Model for Blood Flow in Magnetic Field,” Physics of Fluids, Vol. 17, 2005, pp. 077107-077115. doi:10.1063/1.1978807
- Y. Haik, V. Pai and C. J. Chen, “Apparent Viscosity of Human Blood in a High Static Magnetic Field,” Magnetism and Magnetic Material, Vol. 225, No. 14, 2001, pp. 180-186. doi:10.1016/S0304-8853(00)01249-X
- V. P. Srivastava and M. Saxena, “Two-Layered Model of Casson Fluid Flow through Stenotic Blood Vessels; Apllications to the Cardiovascular System,” Journal of Biomechanics, Vol. 27, 1994, pp. 921-928. doi:10.1016/0021-9290(94)90264-X
- D. F. Fry, “Acute Vascular Emdothelial Changes Associated with Increased Blood Velocity Gradients,” Circulation Research, Vol. 22, 1968, pp. 165-197.

