Applied Mathematics
Vol. 3 No. 3 (2012) , Article ID: 18094 , 6 pages DOI:10.4236/am.2012.33036
Common Fixed Point Theorem in Intuitionistic Fuzzy Metric Space Using R-Weakly Commuting Mappings
1School of Mathematics and Computer Applications, Thapar University, Patiala, India
2Deenbandhu Chhotu Ram, University of Science and Technology, Murthal, India
Email: *sauravmanro@hotmail.com
Received August 22, 2011; revised October 10, 2011; accepted October 18, 2011
Keywords: Intuitionistic Fuzzy Metric Space; Reciprocal Continuity; R-Weakly Commuting Mappings; Common Fixed Point Theorem
ABSTRACT
In this paper, we prove a common fixed point theorem in Intuitionistic fuzzy metric space by using pointwise R-weak commutativity and reciprocal continuity of mappings satisfying contractive conditions.
1. Introduction
Atanassove [1] introduced and studied the concept of intuitionistic fuzzy sets as a generalization of fuzzy sets. In 2004, Park [2] defined the notion of intuitionistic fuzzy metric space with the help of continuous t-norms and continuous t-conorms. Recently, in 2006, Alaca et al. [3] defined the notion of intuitionistic fuzzy metric space by making use of Intuitionistic fuzzy sets, with the help of continuous t-norm and continuous t-conorms as a generalization of fuzzy metric space due to Kramosil and Michalek [4]. In 2006, Turkoglu [5] et al. proved Jungck’s [6] common fixed point theorem in the setting of intuitionistic fuzzy metric spaces for commuting mappings. For more details on intuitionistic fuzzy metric space, one can refer to the papers [7-12].
The aim of this paper is to prove a common fixed point theorem in intuitionistic fuzzy metric space by using pointwise R-weak commutativity [5] and reciprocal continuity [9] of mappings satisfying contractive conditions.
2. Preliminaries
Definition 2.1 [13]. A binary operation 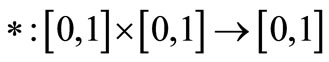 is continuous t-norm if * satisfies the following conditions:
is continuous t-norm if * satisfies the following conditions:
1) * is commutative and associative;
2) * is continuous;
3) 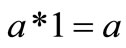 for all
for all ;
;
4)  whenever
whenever 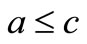 and
and  for all
for all 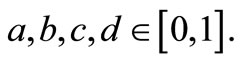
Definition 2.2 [13]. A binary operation  is continuous t-conorm if ◊ satisfies the following conditions:
is continuous t-conorm if ◊ satisfies the following conditions:
1) ◊ is commutative and associative;
2) ◊ is continuous;
3)  for all
for all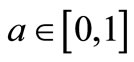 ;
;
4)  whenever
whenever  and
and 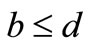 for all
for all 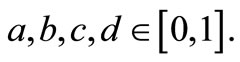
Alaca et al. [3] defined the notion of intuitionistic fuzzy metric space as:
Definition 2.3 [3]. A 5-tuple 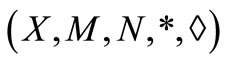 is said to be an intuitionistic fuzzy metric space if X is an arbitrary set, * is a continuous t-norm, ◊ is a continuous tconorm and
is said to be an intuitionistic fuzzy metric space if X is an arbitrary set, * is a continuous t-norm, ◊ is a continuous tconorm and 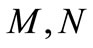 are fuzzy sets on X2 × [0, ∞) satisfying the conditions:
are fuzzy sets on X2 × [0, ∞) satisfying the conditions:
1) 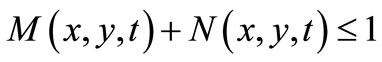 for all
for all 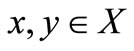 and
and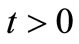 ;
;
2)  for all
for all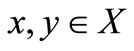 ;
;
3) 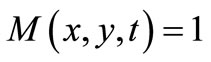 for all
for all 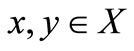 and
and 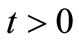 if and only if
if and only if ;
;
4)  for all
for all  and t > 0;
and t > 0;
5)  for all
for all 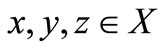 and
and ;
;
6) 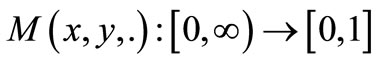 is left continuous, for all
is left continuous, for all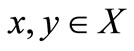 ;
;
7)  for all
for all 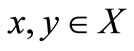 and
and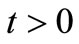 ;
;
8) 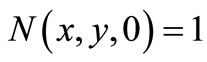 for all
for all ;
;
9) 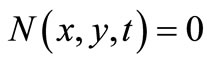 for all
for all 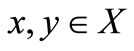 and
and 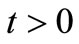 if and only if
if and only if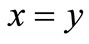 ;
;
10) 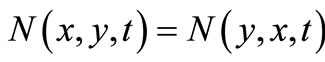 for all
for all 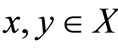 and t > 0;
and t > 0;
11) 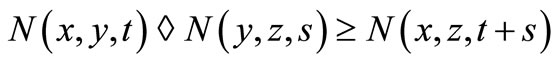 for all
for all 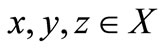 and
and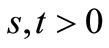 ;
;
12) 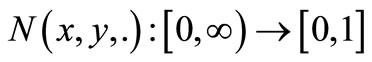 is right continuous, for all
is right continuous, for all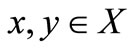 ;
;
13)  for all
for all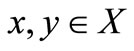 .
.
The functions  and
and  denote the degree of nearness and the degree of non-nearness between x and y w.r.t. t respectively.
denote the degree of nearness and the degree of non-nearness between x and y w.r.t. t respectively.
Remark 2.1 [12]. Every fuzzy metric space 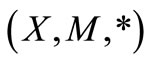 is an intuitionistic fuzzy metric space of the form
is an intuitionistic fuzzy metric space of the form 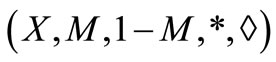 such that t-norm * and t-conorm
such that t-norm * and t-conorm  are associated as
are associated as 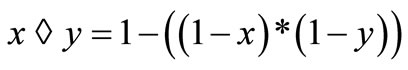 for all
for all .
.
Remark 2.2 [12]. In intuitionistic fuzzy metric space ,
, 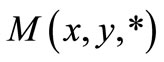 is non-decreasing and
is non-decreasing and 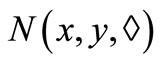 is non-increasing for all
is non-increasing for all .
.
Definition 2.4 [3]. Let 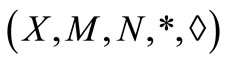 be an intuitionistic fuzzy metric space. Then
be an intuitionistic fuzzy metric space. Then
1) A sequence 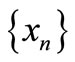 in X is said to be Cauchy sequence if, for all
in X is said to be Cauchy sequence if, for all 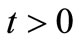 and
and ,
,
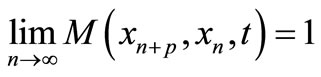
and

2) A sequence 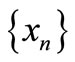 in X is said to be convergent to a point
in X is said to be convergent to a point 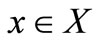 if, for all
if, for all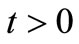 ,
,

and
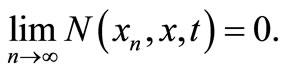
Definition 2.5 [3]. An intuitionistic fuzzy metric space 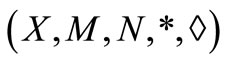 is said to be complete if and only if every Cauchy sequence in X is convergent.
is said to be complete if and only if every Cauchy sequence in X is convergent.
Example 2.1 [3]. Let 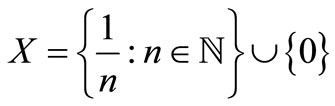 and let * be the continuous t-norm and ◊ be the continuous tconorm defined by
and let * be the continuous t-norm and ◊ be the continuous tconorm defined by 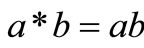 and
and 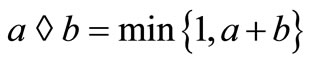 respectively, for all
respectively, for all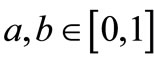 . For each
. For each  and
and , define M and N by
, define M and N by
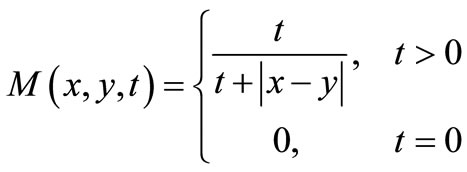
and
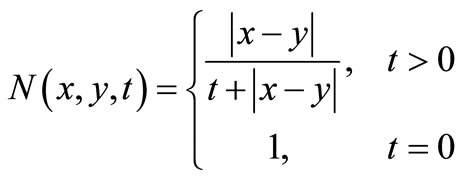
Clearly, 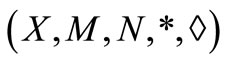 is complete intuitionistic fuzzy metric space.
is complete intuitionistic fuzzy metric space.
Definition 2.6 [3]. A pair of self mappings 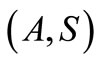 of a intuitionistic fuzzy metric space
of a intuitionistic fuzzy metric space 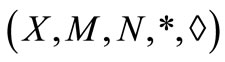 is said to be commuting if
is said to be commuting if  and
and  for all
for all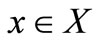 .
.
Definition 2.7 [3]. A pair of self mappings 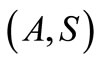 of a intuitionistic fuzzy metric space
of a intuitionistic fuzzy metric space  is said to be weakly commuting if
is said to be weakly commuting if  and
and 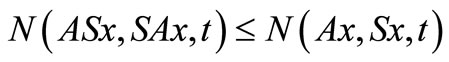 for all
for all  and
and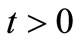 .
.
Definition 2.8 [12]. A pair of self mappings 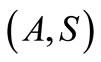 of a intuitionistic fuzzy metric space
of a intuitionistic fuzzy metric space  is said to be compatible if
is said to be compatible if 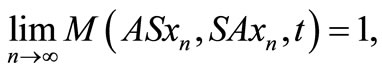 and
and 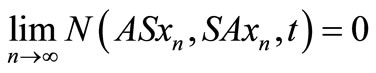 for all
for all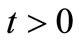 , whenever
, whenever  is a sequence in X such that
is a sequence in X such that  for some
for some 
Definition 2.9 [5]. A pair of self mappings 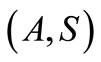 of a intuitionistic fuzzy metric space
of a intuitionistic fuzzy metric space 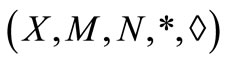 is said to be pointwise R-weakly commuting, if given
is said to be pointwise R-weakly commuting, if given , there exist
, there exist 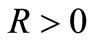 such that for all
such that for all 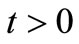
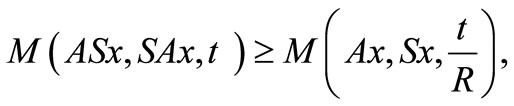
and
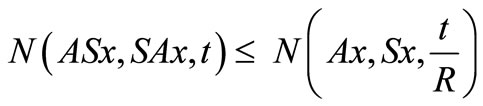
Clearly, every pair of weakly commuting mappings is pointwise R-weakly commuting with .
.
Definition 2.10 [9]. Two mappings A and S of a Intuitionistic fuzzy metric space  are called reciprocally continuous if
are called reciprocally continuous if 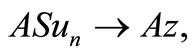
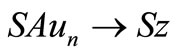 , whenever
, whenever 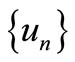 is a sequence such that
is a sequence such that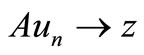 ,
, 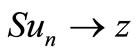 for some z in X.
for some z in X.
If A and S are both continuous, then they are obviously reciprocally continuous but converse is not true.
3. Lemmas
The proof of our result is based upon the following lemmas of which the first two are due to Alaca et al. [12]:
Lemma 3.1 [12]. Let 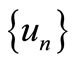 is a sequence in a intuitionistic fuzzy metric space
is a sequence in a intuitionistic fuzzy metric space . If there exists a constant
. If there exists a constant  such that
such that
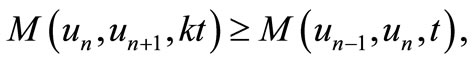
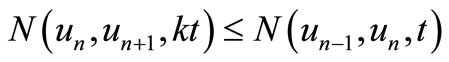
for all 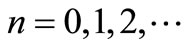
Then 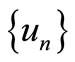 is a Cauchy sequence in X.
is a Cauchy sequence in X.
Lemma 3.2 [12]. Let 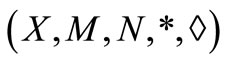 be intuitionistic fuzzy metric space and for all
be intuitionistic fuzzy metric space and for all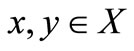 ,
, 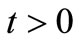 and if for a number
and if for a number 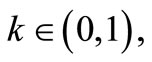
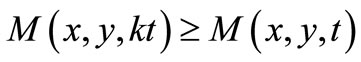 and
and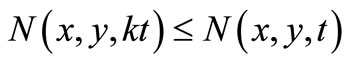 . Then x = y.
. Then x = y.
Lemma 3.3. Let  be a complete intuitionistic fuzzy metric space with continuous t-norm * and continuous t-conorm ◊ defined by
be a complete intuitionistic fuzzy metric space with continuous t-norm * and continuous t-conorm ◊ defined by 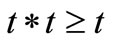 and
and 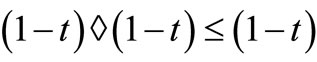 for all
for all 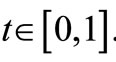 Further, let
Further, let 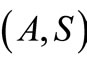 and
and 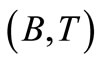 be pointwise R-weakly commuting pairs of self mappings of X satisfying:
be pointwise R-weakly commuting pairs of self mappings of X satisfying:
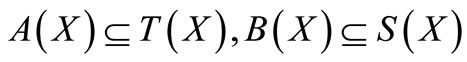
(3.2) there exists a constant 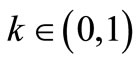 such that
such that


for all ,
, 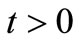 and
and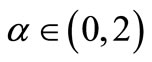 . Then the continuity of one of the mappings in compatible pair
. Then the continuity of one of the mappings in compatible pair  or
or  on
on 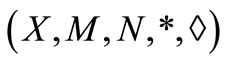 implies their reciprocal continuity.
implies their reciprocal continuity.
Proof. First, assume that A and S are compatible and S is continuous. We show that A and S are reciprocally continuous. Let 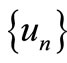 be a sequence such that
be a sequence such that 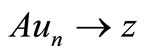 and
and 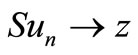 for some
for some  as
as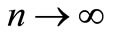 .
.
Since S is continuous, we have 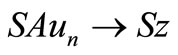 and
and 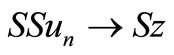 as
as 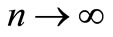 and since
and since 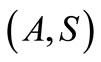 is compatible, we have
is compatible, we have
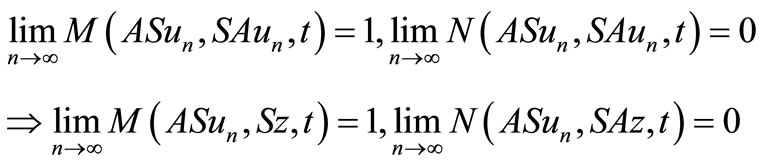
That is 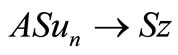 as
as . By (3.1), for each n, there exists
. By (3.1), for each n, there exists 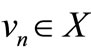 such that
such that 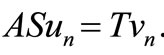 Thus, we have
Thus, we have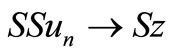 ,
, 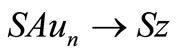 ,
, 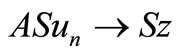 and
and  as
as 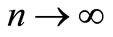 whenever
whenever 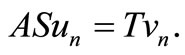
Now we claim that 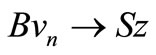 as
as .
.
Suppose not, then taking 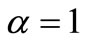 in (3.2), we have
in (3.2), we have
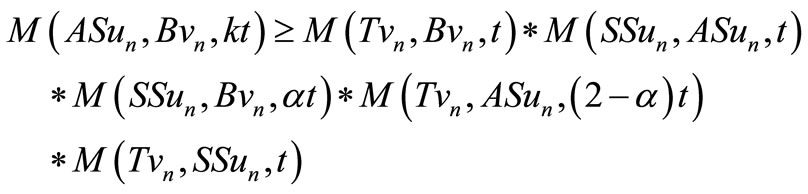
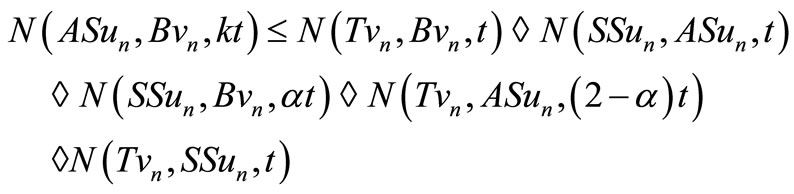
Taking , we get
, we get

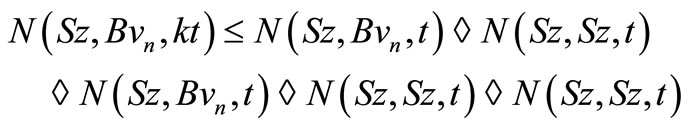
That is,

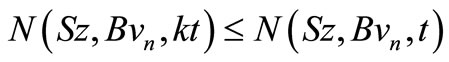
by the use of Lemma 3.2, we have  as
as .
.
Now, we claim that 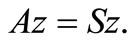 Again take
Again take  in (3.2), we have
in (3.2), we have
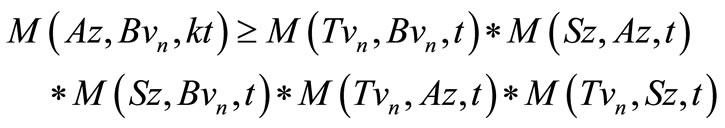
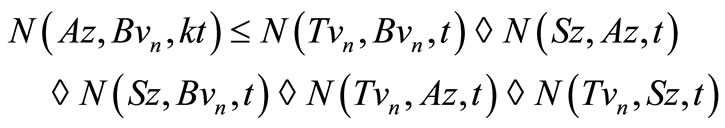
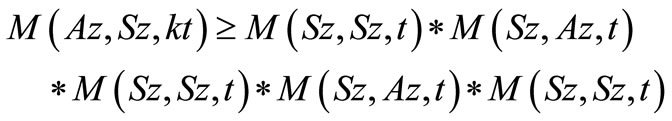
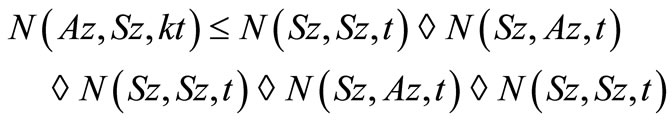
i.e.


therefore, by use of Lemma 3.2, we have 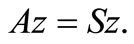
Hence, 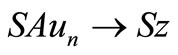 ,
, 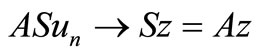 as
as .
.
This proves that A and S are reciprocally continuous on X. Similarly, it can be proved that B and T are reciprocally continuous if the pair 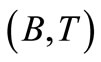 is assumed to be compatible and T is continuous.
is assumed to be compatible and T is continuous.
4. Main Result
The main result of this paper is the following theorem:
Theorem 4.1. Let 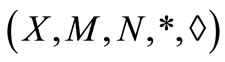 be a complete intuitionistic fuzzy metric space with continuous t-norm * and continuous t-conorm
be a complete intuitionistic fuzzy metric space with continuous t-norm * and continuous t-conorm  defined by
defined by 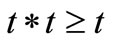 and
and  for all
for all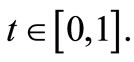
Further, let 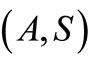 and
and 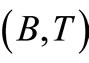 be pointwise R-weakly commuting pairs of self mappings of X satisfying (3.1), (3.2). If one of the mappings in compatible pair
be pointwise R-weakly commuting pairs of self mappings of X satisfying (3.1), (3.2). If one of the mappings in compatible pair 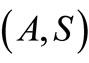 or
or 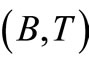 is continuous, then A, B, S and T have a unique common fixed point.
is continuous, then A, B, S and T have a unique common fixed point.
Proof. Let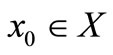 . By (3.1), we define the sequences
. By (3.1), we define the sequences 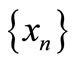 and
and  in X such that for all
in X such that for all 
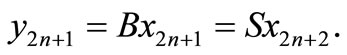
 We show that
We show that 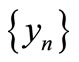 is a Cauchy sequence in X. By (3.2) take
is a Cauchy sequence in X. By (3.2) take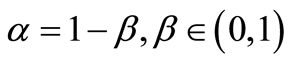 , we have
, we have
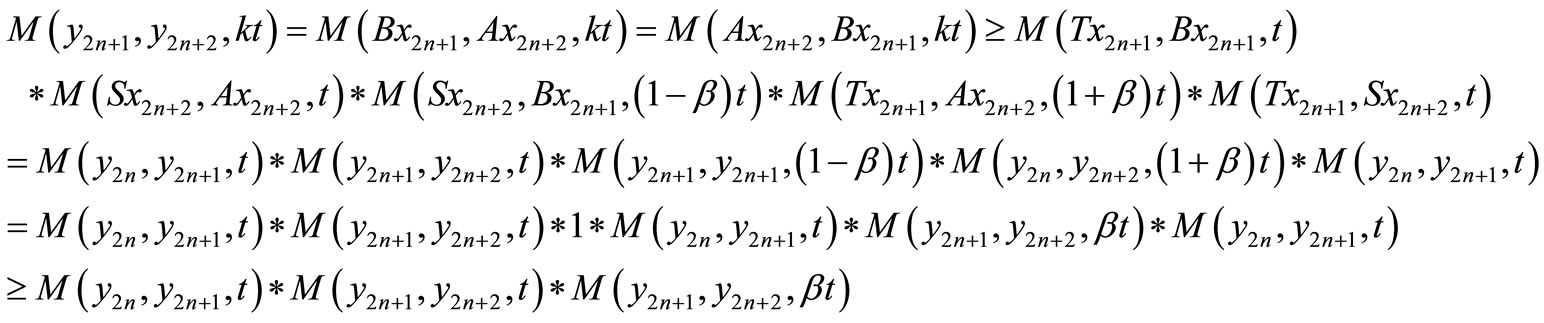
Now, taking , we have
, we have
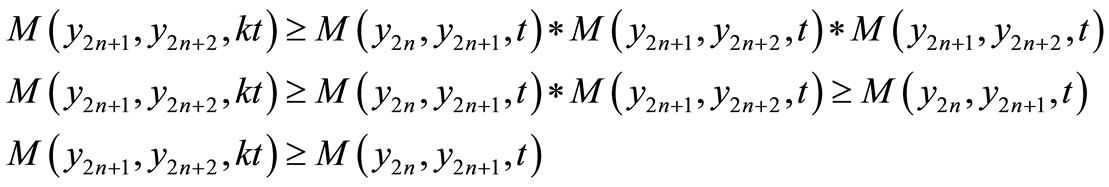
Similarly, we can show that
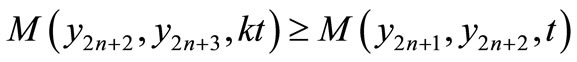
Also,

Taking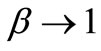 , we get
, we get
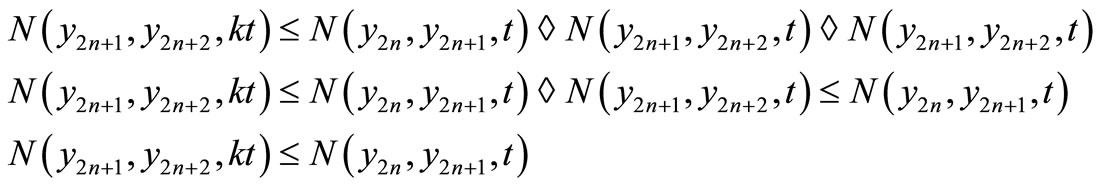
Similarly, it can be shown that
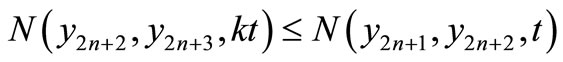
Therefore, for any n and t, we have

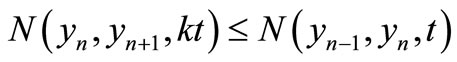
Hence, by Lemma 3.1, 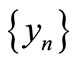 is a Cauchy sequence in X. Since X is complete, so
is a Cauchy sequence in X. Since X is complete, so 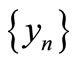 converges to z in X. Its subsequences
converges to z in X. Its subsequences

 and
and  also converge to z.
also converge to z.
Now, suppose that 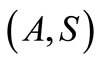 is a compatible pair and S is continuous. Then by Lemma 3.2, A and S are reciprocally continuous, then
is a compatible pair and S is continuous. Then by Lemma 3.2, A and S are reciprocally continuous, then ,
, 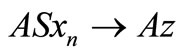 as
as .
.
As,  is a compatible pair. This implies
is a compatible pair. This implies
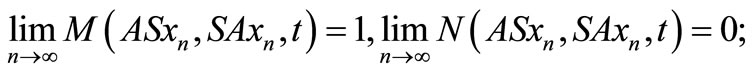
This gives 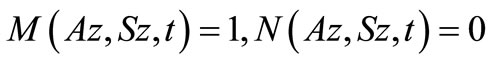 as
as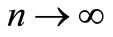 .
.
Hence,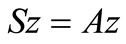 .
.
Since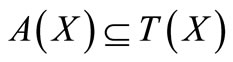 , therefore there exists a point
, therefore there exists a point 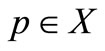 such that
such that 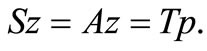
Now, again by taking 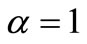 in (3.2), we have
in (3.2), we have
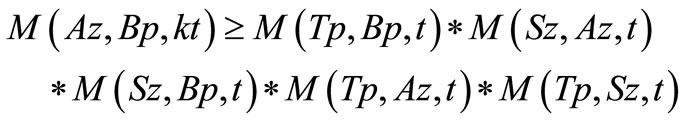
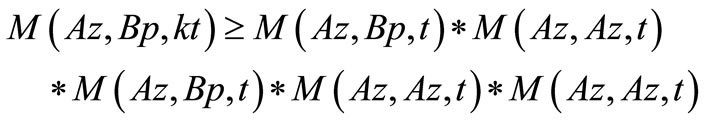
and
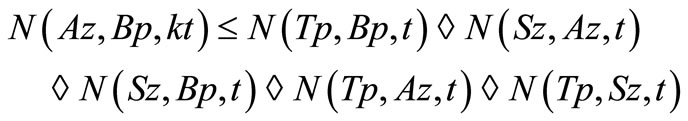
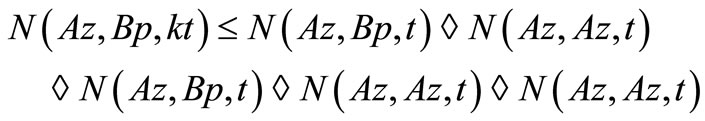
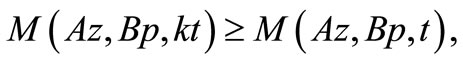
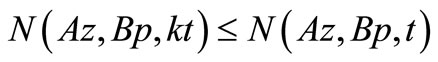
Thus, by Lemma 3.2, we have 
Thus, 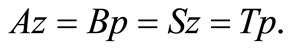
Since, A and S are pointwise R-weakly commuting mappings, therefore there exists , such that
, such that
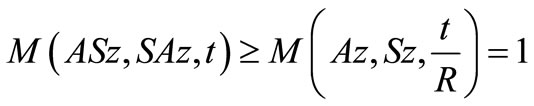
and

Hence, 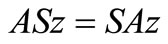 and
and 
Similarly, B and T are pointwise R-weakly commuting mappings, we have
Again, by taking 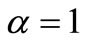 in (3.2),
in (3.2),
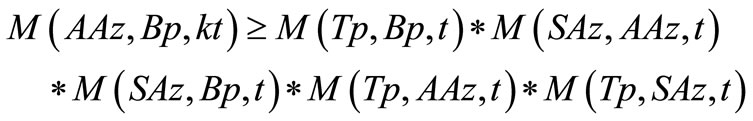
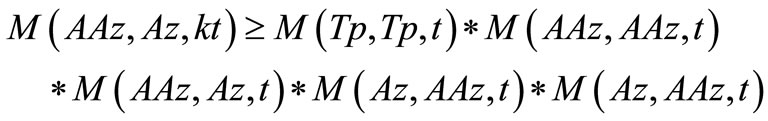
and
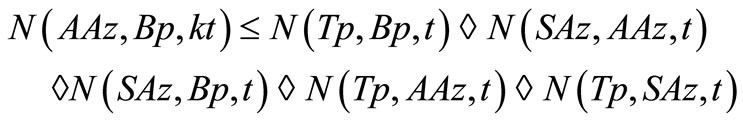

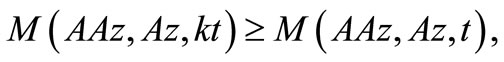
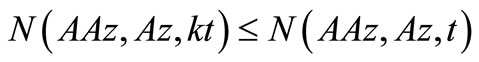
By Lemma 3.2, we have  Hence
Hence 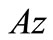 is common fixed point of A and S. Similarly by (3.2),
is common fixed point of A and S. Similarly by (3.2), 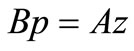 is a common fixed point of B and T. Hence,
is a common fixed point of B and T. Hence, 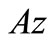 is a common fixed point of A, B, S and T.
is a common fixed point of A, B, S and T.
Uniqueness: Suppose that 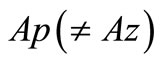 is another common fixed point of A, B, S and T.
is another common fixed point of A, B, S and T.
Then by (3.2), take 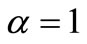

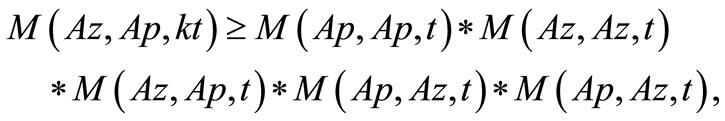 and
and
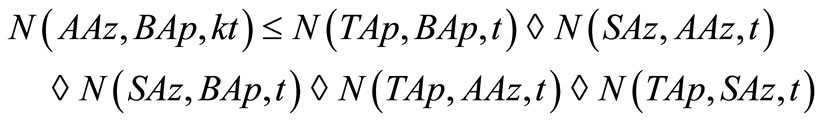

This gives
 and
and
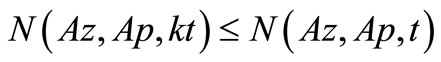
By Lemma 3.2, 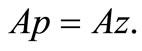
Thus, uniqueness follows.
Taking 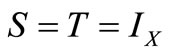 in above theorem, we get following result:
in above theorem, we get following result:
Corollary 4.1. Let 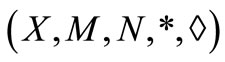 be a complete intuitionistic fuzzy metric space with continuous t-norm * and continuous t-conorm
be a complete intuitionistic fuzzy metric space with continuous t-norm * and continuous t-conorm  defined by
defined by  and
and 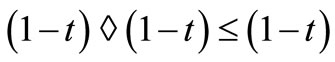 for all
for all 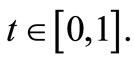 Further, let A and B are reciprocally continuous mappings on X satisfying
Further, let A and B are reciprocally continuous mappings on X satisfying
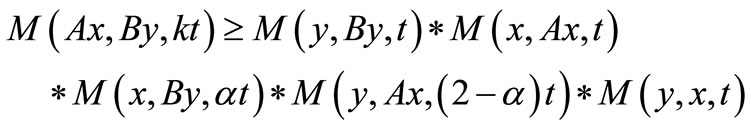
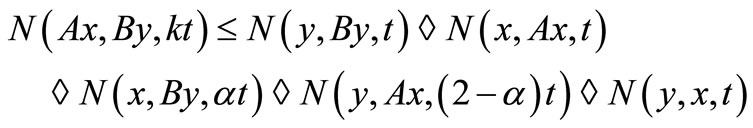
for all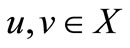 ,
, 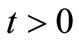 and
and 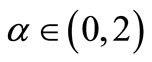 then pair A and B has a unique common fixed point.
then pair A and B has a unique common fixed point.
We give now example to illustrate the above theorem:
Example 4.1. Let 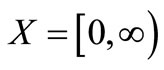 and let
and let  and
and  be defined by
be defined by 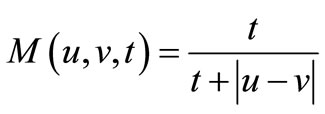
and 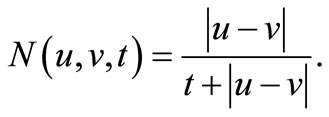
Then  is complete intuitionistic fuzzy metric space. Let A, B, S and T be self maps on X defined as:
is complete intuitionistic fuzzy metric space. Let A, B, S and T be self maps on X defined as:
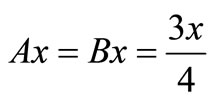 and
and  for all
for all .
.
Clearly
1) either of pair (A, S) or (B, T) be continuous self-mappings on X;
2)  ;
;
3) {A, S} and {B, T} are R-weakly commuting pairs as both pairs commute at coincidence points;
4) {A, S} and {B, T} satisfies inequality (3.2), for all , where
, where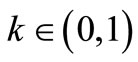 .
.
Hence, all conditions of Theorem 4.1 are satisfied and x = 0 is a unique common fixed point of A, B, S and T.
5. Acknowledgements
We would like to thank the referee for the critical comments and suggestions for the improvement of my paper.
REFERENCES
- K. Atanassov, “Intuitionistic Fuzzy Sets,” Fuzzy Sets and System, Vol. 20, No. 1, 1986, pp. 87-96. doi:10.1016/S0165-0114(86)80034-3
- J. H. Park, “Intuitionistic Fuzzy Metric Spaces,” Chaos, Solitons & Fractals, Vol. 22, No. 5, 2004, pp. 1039-1046. doi:10.1016/j.chaos.2004.02.051
- C. Alaca, D. Turkoglu and C. Yildiz, “Fixed Points in Intuitionistic Fuzzy Metric Spaces,” Chaos, Solitons & Fractals, Vol. 29, No. 5, 2006, pp. 1073-1078. doi:10.1016/j.chaos.2005.08.066
- I. Kramosil and J. Michalek, “Fuzzy Metric and Statistical Metric Spaces,” Kybernetica, Vol. 11, No. 5, 1975, pp. 326-334.
- D. Turkoglu, C. Alaca, Y. J. Cho and C. Yildiz, “Common Fixed Point Theorems in Intuitionistic Fuzzy Metric Spaces,” Journal of Applied Mathematics and Computing, Vol. 22, No. 1-2, 2006, pp. 411-424.
- G. Jungck, “Commuting Mappings and Fixed Points,” American Mathematical Monthly, Vol. 83, No. 4, 1976, pp. 261-263. doi:10.2307/2318216
- S. Manro, S. Kumar and S. Singh, “Common Fixed Point Theorems in Intuitionistic Fuzzy Metric Spaces,” Applied Mathematics, Vol. 1, No. 6, 2010, pp. 510-514.
- S. Manro, H. Bouharjera and S. Singh, “A Common Fixed Point Theorem in Intuitionistic Fuzzy Metric Space by Using Sub-Compatible Maps,” International Journal of Contemporary Mathematical Sciences, Vol. 5, No. 55, 2010, pp. 2699-2707. http://m-hikari.com/ijcms-2010/53-56-2010/manroIJCMS53-56-2010.pdf
- S. Muralisankar and G. Kalpana, “Common Fixed Point Theorems in Intuitionistic Fuzzy Metric Spaces Using Reneral Contractive Condition of Integral Type,” International Journal of Contemporary Mathematical Sciences, Vol. 4, No. 11, 2009, pp. 505-518. http://www.m-hikari.com/ijcms-password2009/9-12-2009/muralisankarIJCMS9-12-2009.pdf
- D. Turkoglu, C. Alaca and C. Yildiz, “Compatible Maps and Compatible Maps of Type (α) and (β) in Intuitionistic Fuzzy Metric Spaces,” Demonstratio Mathematica, Vol. 39, No. 3, 2006, pp. 671-684. http://demmath.mini.pw.edu.pl/pdf/dm39_3.pdf
- D. Turkoglu, C. Alaca and C. Yildiz, “Common Fixed Point Theorems of Compatible Maps in Intuitionistic Fuzzy Metric Spaces,” Southeast Asian Bulletin of Mathematics, Vol. 32, 2008, pp. 21-33. http://seams-bull-math.scnu.edu.cn/
- C. Alaca, I. Altun and D. Turkoglu, “On Compatible Mappings of Type (I) and (II) in Intuitionistic Fuzzy Metric Spaces,” Communications of the Korean Mathematical Society, Vol. 23, No. 3, 2008, pp. 427-446. http://mathnet.or.kr/mathnet/thesis_file/14_C07-110.pdf
- B. Schweizer and A. Sklar, “Probabilistic Metric Spaces,” North Holland Series in Probability and Applied Mathematics, North-Holland, New York, Vol. 16, 1983, pp. 54- 77.
NOTES
*Corresponding author.

